复杂仿真实验结果可信度评估方法

胡晓峰,李 伟,马 萍,杨 明

(哈尔滨工业大学 控制与仿真中心,黑龙江 哈尔滨 150001)

0 引言

仿真技术是以相似原理、模型理论、系统技术、信息技术及仿真应用领域的有关专业技术为基础,以计算机系统、与应用有关的物理效应及仿真器为工具,利用系统模型对实际或设想的系统进行研究、分析、实验与运行的一门多学科综合性技术[1]。由于仿真技术在应用上具有经济性、安全性、可重复性、无破坏性等优点,所以在许多复杂系统上有着广泛应用。可信度是仿真技术应用的关键指标之一,直接关系到仿真应用的成败。因此,仿真可信度评估一直以来都是研究热点。

可信度评估是指对模型、仿真系统、仿真实验结果是否可信和可信程度进行分析、计算和评价[2]。目前,仿真模型可信度评估方法大多集中在仿真结果验证方面。在定性验证方面,主要方法有表面验证法和图灵测试法。在定量验证方面,用于静态结果验证的方法有假设检验和参数估计法,如t检验、χ2检验和K-S检验、区间估计等,而用于动态结果验证的方法有Theil不等系数法、灰色关联分析法、频谱分析法等。仿真系统的可信度评估方法主要是一些综合性评估方法,如层次分析法[3]、模糊综合评判方法[4]、基于Bayes网络的方法[5]等。仿真实验结果的可信度评估方法相对较少。如豆建斌等[6]在仿真系统可信度评估的基础上将仿真实验设备和仿真结果可信度纳入仿真实验的可信度评估;綦磊升等[7]以数据、模型、仿真实验系统和仿真结果的可信性为依据,采用模糊层次分析法对指挥信息系统仿真试验的可信性进行评估。

综上所述,关于仿真模型/系统的可信度评估方法研究比较成熟,而针对仿真实验结果的可信度评估方法的研究较少,而且现有研究忽略了仿真实验方案的影响。为此,本文将开展复杂仿真实验结果的可信度评估方法研究。首先,根据复杂仿真实验的特点,构建仿真实验结果的可信度评估指标体系;然后,重点研究仿真实验的可信度评估指标度量方法和指标综合方法;最后,通过实例说明空间填充性和正交性度量准则的适用性。

1 仿真实验结果的可信度评估指标体系

指标体系是评估工作的基础。建立准确清晰、科学合理的评估指标体系对仿真实验结果的可信度评估具有重要意义。仿真实验结果的可信度评估包含许多因素,运用层次化方法将互相联系的有序层次进行划分,使之条理化,是建立指标体系的有效途径。仿真实验结果是在仿真系统上进行实验产生的输出,因此仿真实验结果的可信度和仿真实验及仿真系统的可信度有关。仿真实验结果的可信度评估指标体系应包含仿真实验的可信度和仿真系统的可信度2个部分,如图1所示。其中,仿真系统的可信度评估指标体系和方法相对成熟,本文主要研究复杂仿真实验的可信度评估指标体系。

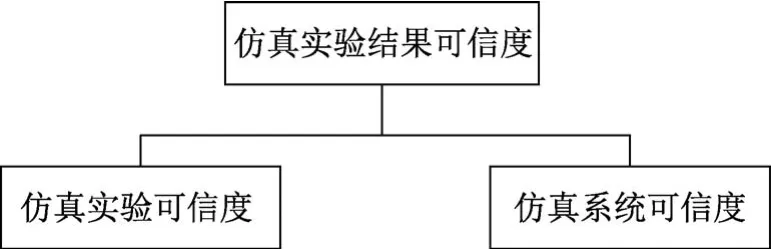
图1 仿真实验结果可信度评估指标体系Fig.1 Credibility assessment index system for simulation experiment results

复杂仿真实验具有因子数多、因子水平数多、考虑指标数多、实验运行次数多、获得的实验数据多等特点。因此,本文主要从运行层实验的可信度和想定层实验的可信度2个方面来评估复杂仿真实验的可信度,如图2 所示。运行层实验的可信度主要受仿真输出精度的影响。仿真输出精度与仿真重复运行次数有关,是随机不确定性的体现,重复运行次数不足会放大仿真实验的不确定性,从而降低仿真实验的可信度。想定层实验的可信度主要由实验点的空间填充性、正交性、分布一致性和典型性4 个指标来度量。其中,空间填充性能保证在参数响应函数不明确时,通过抽样获得整个样本空间的信息;正交性用来衡量实验点之间的相关性,能够增强分析评估因素对实验指标的影响和各因素的交互作用能力;分布一致性用来检验实验点因素分布是否符合实际系统因素分布,可以保证实验点选取的有效性;典型性要求实验点的选择具有典型性、代表性,尽可能将最佳效应点包括在内,否则很难达到预期目的。

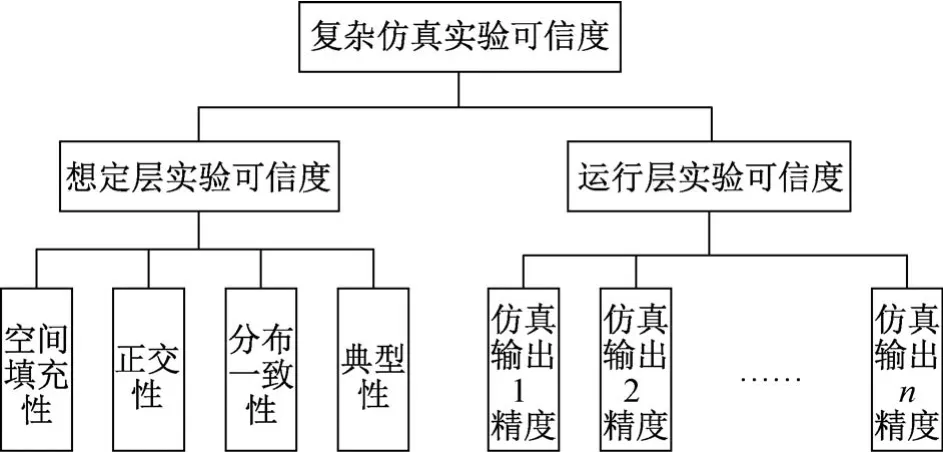
图2 复杂仿真实验可信度评估指标体系Fig.2 Credibility assessment index system for complex simulation experiment

想定层实验的可信度评估指标与实验目的密切相关,而且目的不同指标也不同。复杂仿真实验的目的主要有：1)确定影响系统输出的因素主次,获得实验因素对系统输出的影响规律;2)确定系统输出和实验因素之间的近似函数关系,对输出进行预测和优化;3)确定最优方案,寻找最优实验点;4)验证与评估,验证方案是否可行、评估系统性能等。其中：类型1常采用方差分析,而方差分析需要的实验点必须具有整齐可比的特点,即对实验样本的正交性有要求;类型2常采用回归分析,而回归分析的准确性与样本空间的信息量有关,信息量越多,分析越准确,即对样本的空间填充性有要求;类型3一般需要样本空间的信息量大,且实验具有“均衡搭配性”“综合可比性”,对样本空间填充性和正交性也有一定要求;类型4需要样本在空间分布范围广,具有一定代表性,通常对样本的空间填充性和典型性有要求。而分布一致性一般在实验样本数量较多的情况下采用,用于检验仿真实验的样本分布和实际系统是否一致。

2 仿真实验可信度评估指标度量方法

2.1 仿真输出精度度量方法

仿真输出的精度和实验重复运行次数有关。一般来说,实验重复运行次数越大,仿真输出的相对误差越小,输出精度越高。因此,可以通过相对误差来度量仿真输出的精度。常用置信区间法来计算实验输出的相对误差[8]。

可通过置信区间的计算公式来验证置信区间与样本量的关系。对于实验方案A,重复运行n次,假设第i次仿真运行对应的输出为o i,则o1,o2,…,o n的均值就是期望μ=E(o)的无偏估计。μ置信度为100(1-α)的置信区间为

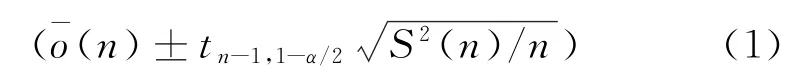
式中：n为方案运行次数;t n-1,1-α/2为自由度是n-1,置信度是100(1-α)t分布的上分位数;S(n)为样本o1,o2,…,o n的标准偏差,其计算方法为

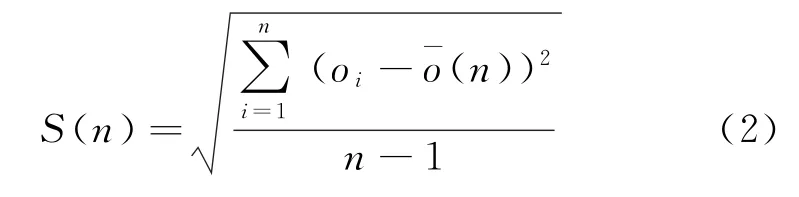
而相对误差的估计值为

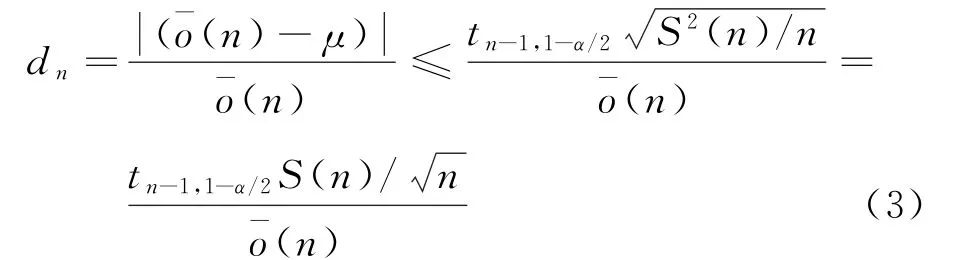
式中：t n-1,1-α/2随着实验次数n的增加而减小;随实验次数n增加而逐步收敛到某值。因此,d n随实验次数n不断增加而逐渐减小。

实验输出的相对误差d n需要满足0≤d n≤1,而且d n越小,仿真输出的精度就越大,因此采用式(4)来表示仿真输出的精度,即

2.2 空间填充性度量方法

空间填充性度量准则也称作充满空间(spacefilling)准则,可分为基于距离(distance-based)、基于均匀性(uniformity-based)、基于熵(entropybased)[9]等准则。其中,基于均匀性准则(即基于离差的准则)不但可以评估抽样点在d维立方体[0,1]d中的均匀性,而且还能保证其在低维中投影的均匀性,因此常用于度量仿真实验的空间填充性。

离差度量方法主要有中心L2-离差、可卷L2-离差和混合离差(mixture discrepancy,MD)。其中,中心L2-离差更关心顶点附近的点,对于中心区域的点的敏感度较低;可卷L2-离差在各因子平移变换时,其结果不变;而混合离差能够较好克服两者的缺点[11],因此本文采用混合离差度量仿真实验的空间填充性。对于点集P(X1,X2,…,X n)∈C s,X i=(x i1,x i2,…,x is)',它的混合离差为

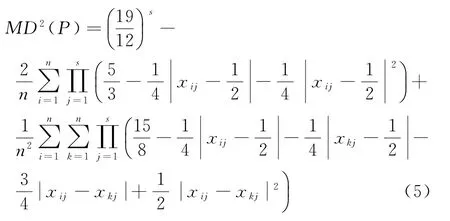
混合离差的计算结果越小,表明实验点的均匀性越好。利用多目标优化算法可以求得相应实验条件下,混合离差的上界MDu和下界MDl,从而得到空间填充性的度量,即

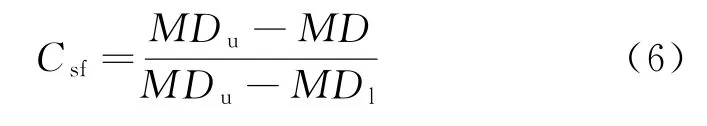
2.3 正交性度量方法

常用的正交性度量准则是实验设计矩阵因素间的相关系数ρ[12],即

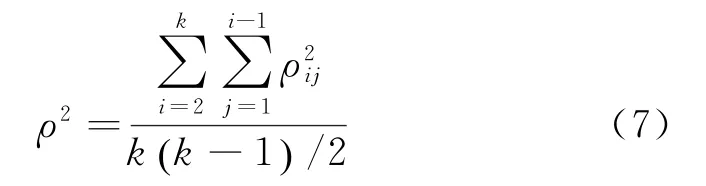
式中：ρij表示实验设计矩阵列向量X i=[x1ix2ix ni]和X j=[x1jx2jx nj]间的线性相关系数,即

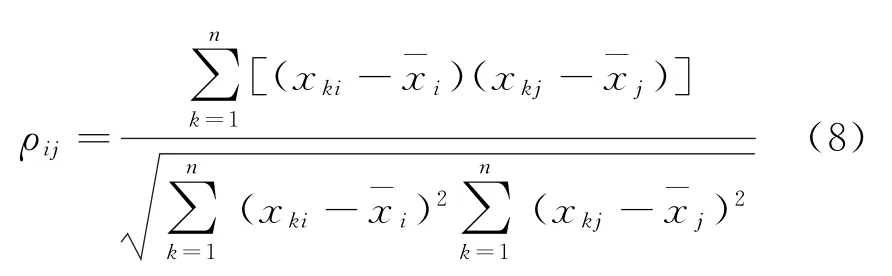
实验设计矩阵因素间的相关系数ρ需要满足0≤ρ≤1,ρ越小,表明正交程度越高。因此,仿真实验正交性的度量公式为

2.4 分布一致性和典型性度量方法

实际系统因素在某些情况下具有一定分布规律,因此可通过度量实验点和实际系统因素分布的一致性来分析实验设计方案的优劣。当已知实际系统的因素分布时,可对仿真实验的点因素进行假设检验,从而判断仿真实验点和实际系统的因素分布是否一致。一致性程度越好,表明实验点的选取越符合实际情况,实验结果越值得信赖。

当实际系统的因素分布为正态分布时,可采用参数检验法进行一致性检验,如U检验、t检验、χ2检验等。当实际系统的因素分布不是正态分布时,可采用非参数检验法进行一致性检验,如χ2拟合检验、秩和检验、K-S检验等。当根据检验样本作出接受原假设H0的推断时,规定此时的分布一致性为1-α;当作出接受备择假设H1的推断时,规定此时的分布一致性为α。

实验点的典型性度量相对简单,可以通过仿真实验点对预设典型点的覆盖程度来计算,计算方法为

式中：N为预设典型实验点个数,N∈Z+;N e为仿真实验点包含的预设典型点个数,为大于等于0的整数。

3 仿真实验结果可信度评估指标综合方法

评估指标计算结果需采用指标综合方法得到最终的仿真实验结果的可信度。常用的指标综合方法有加法合成法和乘法合成法。

1)加法合成法。加法合成法,又称线性加权法,是指在指标值和指标权重已知的情况下直接加权平均得到评估结果的方法。评估层次分析法中的上层指标即使用该方法,其表达式为

该方法的基本思想是“部分之和即整体”,要求各指标相互独立。不相互独立的指标,指标间有交互信息,和的结果会导致信息的重复,使得评估结果不能反映实际情况。而且,由于各指标权重之和恒等于1,造成各指标“此消彼长”“相互补偿”,即如果某指标权重减小,则一定会以指标权重增大来补偿。因此,加法合成法在许多情况下对不同对象间的指标值的差异不敏感。此外,加法合成法对数据的要求不高,无论指标值和权重是什么形式的取值都能得到评估结果。

2)乘法合成法。乘法合成法常用于指标间关联程度较强的评估问题中,即某个指标的变化会对其他指标产生影响,从而导致整体评价结果产生变化。比如在仿真实验结果的可信度评估问题中,仿真实验是在仿真系统可信的基础上进行的,即仿真实验与仿真系统关联。因此,仿真实验结果的可信度由仿真系统的可信度和仿真实验的可信度相乘得到。乘法合成法一般有2种表现形式,即

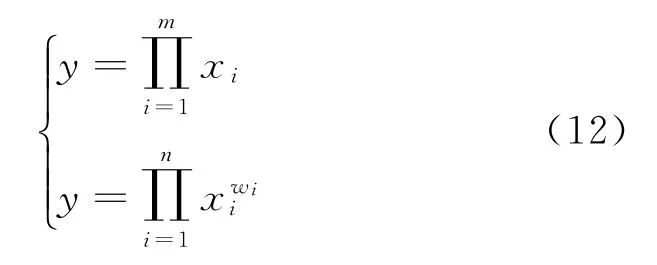
该类方法对指标权重的要求不高,必要时可令各指标权重相等。但该类方法对指标值的要求比较高,尤其是对指标值中的较小值比较敏感,某一指标的变化会对整个评估结果造成较大的影响。因此,各指标需要均衡发展,避免出现“一损俱损”的局面。

综上所述：在综合评估问题中,加法合成法常用于指标相互独立、指标权重差异较大的情况;乘法合成法常用于指标相关联、指标权重差异不大、指标值有差异的情况。复杂仿真实验结果的可信度评估问题中,运行层实验与想定层实验相关联,仿真实验的可信度由想定层实验可信度和运行层实验可信度相乘得到。仿真实验结果的可信度由仿真系统可信度和仿真实验可信度相乘得到,其余上层指标通过加法合成法求得,如图3,4所示。

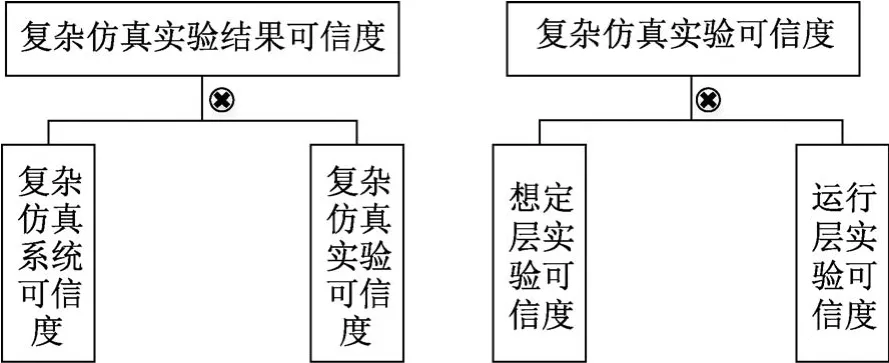
图3 乘法合成法应用Fig.3 Application of multiplicative synthesis

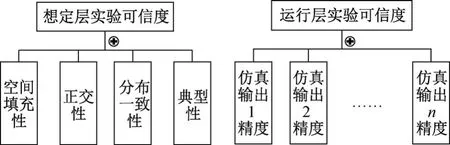
图4 加法合成法应用Fig.4 Application of additive synthesis

上述指标综合的描述为：c ai为仿真输出i的精度,i=1,2,…,n;v i为想定层实验可信度的底层指标值,i=1,2,3,4;c e1为运行层实验可信度;c e2为想定层实验可信度;c e为仿真实验可信度;c s为仿真系统可信度;c为仿真实验结果可信度。

指标综合公式为

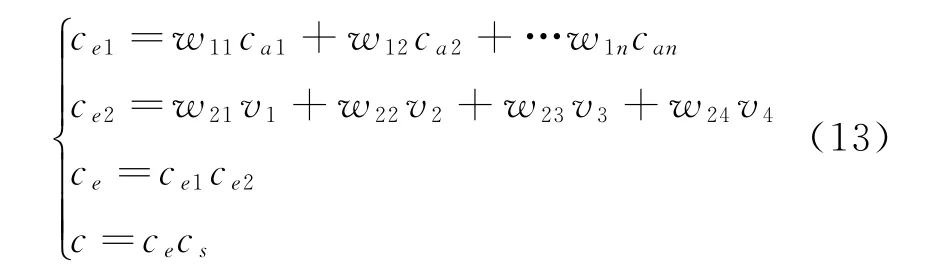
式中：w1i是仿真输出i精度的权重,0≤w1i≤1,=1;w2i是想定层实验可信度底层指标的权重,0≤w2i≤1,=1。

4 计算实例

以4种不同优化算法下的拉丁超立方试验设计(Latin hypercube design,LHD(9,4))为例[12-13],给出空间填充性和正交性指标的计算结果,如表1所示。其中,M 代表最大化最小距离准则,O 代表正交性准则,U 代表均匀性准则,OM 代表正交-最大化最小距离准则。

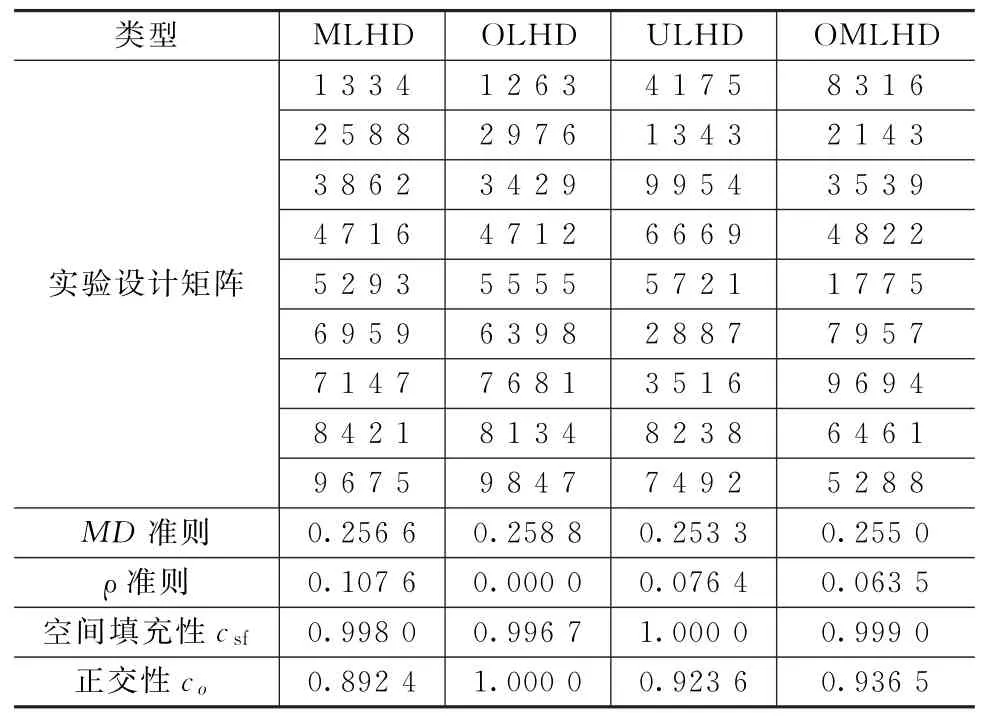
表1 4种LHD空间填充性和正交性对比Tab.1 Comparisons for space-filling and orthogonality of 4 LHD

由表1可以看出：M 准则、U 准则,以及OM 准则下LHD 的空间填充性较优;O 准则、OM 准则下LHD的正交性较好,符合实际情况。说明本文使用的空间填充性和正交性度量准则的适用性较好。

5 结束语

仿真可信度评估是仿真理论的重要组成部分。目前,仿真可信度的评估方法研究主要集中于仿真模型和仿真系统,而对仿真实验结果可信度评估的研究较少。因此,本文提出一种复杂仿真实验结果的可信度评估方法,通过实例验证了空间填充性和正交性度量方法的适用性。该方法不仅可以丰富仿真可信度评估体系,而且可以为应用仿真实验结果的可信度评估提供参考。今后将对仿真实验结果的可信度评估指标体系,以及指标的综合方法进行进一步研究。