基于椭圆曲线的改进RC4算法

陈虹 刘雨朦 肖成龙 郭鹏飞 肖振久

摘 要：针对流密码（RC4）算法存在不变性弱密钥、密钥流序列随机性不高和算法初始状态可以被破解等问题，提出一种基于椭圆曲线的RC4改进算法。该算法利用椭圆曲线、哈希函数和伪随机数产生器生成初始密钥 Key ，在S盒和指针的作用下进行非线性变换最终生成具有高随机性的密钥流序列。美国国家标准与技术研究院（NIST）随机性测试结果表明，改进算法的频率检验、游程检验和Maurer指标比原RC4算法分别高出0.13893， 0.13081和0.232050，能有效防止不变性弱密钥的产生，抵抗“受戒礼”攻击; Key 初始密钥是一个分布均匀的随机数，不存在偏差，能够有效抵御区分攻击;椭圆曲线、哈希函数具有单向不可逆性，伪随机数产生器具有高密码强度， Key 初始密钥猜测赋值困难，不易破解，能够抵抗状态猜测攻击。理论和实验结果表明改进RC4算法的随机性和安全性高于原RC4算法。

关键词：流密码（RC4）算法;密钥流序列;椭圆曲线;哈希函数;随机性

中图分类号： TP309.7; TP393.08

文献标志码：A

Improved RC4 algorithm based on elliptic curve

CHEN Hong， LIU Yumeng*， XIAO Chenglong， GUO Pengfei， XIAO Zhenjiu

School of Software， Liaoning Technical University， Huludao Liaoning 125105， China

Abstract： For the problem that the Rivest Cipher 4 （RC4） algorithm has invariant weak key， the randomness of the key stream sequence is not high and the initial state of the algorithm can be cracked， an improved RC4 algorithm based on elliptic curve was proposed. In the algorithm， the initial key  Key  was generated by using elliptic curve， Hash function and pseudo-random number generator， and a nonlinear transformation was performed under the action of the S-box and the pointer to finally generate a key stream sequence with high randomness. The randomness test carried out by National Institute of Standards and Technology （NIST） shows that the frequency test， run test and Maurer are 0.13893， 0.13081， and 0.232050 respectively higher than those of the original RC4 algorithm， which can effectively prevent the generation of invariant weak keys and resist the "sentence" attack.  Key The initial key is a uniformly distributed random number without deviation， which can effectively resist the distinguishing attack. The elliptic curve and Hash function have one-way irreversibility， the pseudo-random number generator has high password strength，  Key the initial key guess is difficult to assign and is not easy to crack， which can resist the state guessing attack. Theoretical and experimental results show that the improved RC4 algorithm is more random and safe than the original RC4 algorithm.

Key words： Rivest Cipher 4 （RC4） algorithm; key stream sequence; elliptic curve; Hash function; randomness

0 引言

流密碼（Rivest Cipher 4， RC4）加密算法是1987年RSA（Rivest-Shamir-Adleman）公司提出的，它用字节流方式产生的密钥依次加密明文中的每个字节，解密时依次对密文中的每个字节进行解密，是密钥长度可变的对称流加密算法。RC4算法广泛应用于安全套接层（Secure Sockets Layer，SSL）协议、传输层安全（Transport Layer Security，TLS）协议、有线等效保密（Wired Equivalent Privacy，WEP）协议和Wi-Fi保护接入（Wi-Fi Protected Access，WPA）协议等多种网络和数据传输协议。虽然RC4可以加密传输数据，但密钥信息存在不变脆弱性，易被敌手猜测攻击，安全性受到威胁，因此密钥的健壮性直接影响到RC4算法的安全。

RC4算法易受的攻击主要包括区分攻击、弱密钥攻击和状态猜测攻击等。1994年，文献[1]提出了对RC4算法的“故障引入攻击”;1998年，文献[2]提出状态猜测攻击，即假设攻击者能够获得一段足够多的伪随机序列生成算法（Pseudo Random Generation Algorithm，PRGA）输出值并计算出初始状态，则不需要密钥序列即可继续产生输出值，从而破解RC4算法;文献[3-6]证明了RC4算法密钥流的任意连续两个输出字可以不独立或存在偏差，根据这个偏差进行区分攻击，可以恢复RC4算法的初始状态，导致加密信息泄露等严重后果;文献[7]提出了对RC4算法的错误引入攻击;文献[8-11]利用RC4算法存在的不变性弱密钥问题，让RC4算法陷入了“受戒礼”攻击[11];文献[12]通过对经不同种子密钥长度的RC4算法加密的明文的前256Byte进行恢复，提出了对RC4算法的明文恢复攻击。RC4算法存在的不安全问题引起了人们重视，针对以上对RC4算法的攻击已经提出了不少的改进算法，但改进算法仍存在一定的缺陷。如文献[13]中，为了抵御状态猜测攻击和错误引入攻击，在PRGA部分增加了自我检错步骤，但密钥字节序列的输出变得复杂，效率有所降低;文献[14]对RC4算法中PRGA阶段S表的元素交换进行改进;文献[15]提出的可变可修改的置换组合（Variably Modified Permutation Composition， VMPC）算法是RC4的典型改进算法，它对RC4的密钥编制算法（Key Sehedule Algorithm， KSA）部分进行了改进，可以灵活选择算法步骤，但其状态表S盒取值范围很小（0～28-1），随机性不够高导致安全性降低;文献[16]对文献[15]的VMPC算法进行了破解，利用输出值将密钥流序列与随机序列区分开，获得了初始状态，破解了VMPC算法。

本文针对RC4算法易受区分攻击、“受戒礼”攻击和状态猜测攻击等导致安全性降低的问题，提出了一种基于椭圆曲线的RC4改进算法。该改进算法基于椭圆曲线算法产生随机整数，借助哈希函数扩展位数输入到伪随机数产生器中生成伪随机数，并在状态表中进行非线性变换，从而产生用于加解密的流密钥序列。该改进算法具有不可逆性、高安全性和随机性，能有效抵抗区分攻击、“受戒礼”攻击和状态猜测攻击。

1 RC4算法

RC4算法是一种基于非线性变换的流密码算法，从内部结构可分为内部状态S盒、状态变换函数和输出函数，RC4内部状态变化如图1所示。

从运算过程上可分为密钥编制算法KSA和伪随机序列生成算法PRGA。

1）密钥编制算法KSA：设置S盒的初始排列，用可变长度的密钥生成密钥流生成器的初始状态。

2）伪随机序列生成算法PRGA：根据初始状态进行非线性运算，选取随机元素，修改S盒的原始排列顺序，产生与明文或密文进行非线性运算的密钥流序列。

1.1 密钥编制算法KSA

RC4的密钥编制算法KSA用于产生密钥流生成器的初始状态[17-18]，步骤如下：

步骤1  随机选取一个字长为l的密钥Key，初始化S盒;

步骤2  用指针 i t搜索S盒中的每一个位置， i t每更新一次， j t由St-1[ i t]和Key共同计算生成下一個值;

步骤3  将St中的 j t和 i t交换。

RC4初始状态表S0由上面KSA经过N步迭代后生成。RC4的KSA伪代码如下：

作者说明：算法内部运行过程中，将指针所指位置的值互换，所以指针除了代表该位置，还包括该位置所表示的值，可以看作有大小有方向的量。

程序前

KSA：S0[i]=i（i=0，1，…，2n-1），  i 0=0，  j 0=0;

i t= i t-1+1;

j t= j t-1+St-1[ i t-1]+K[ i t-1 mod l];

St[ i t]=St-1[ j t]， S[ j t]=St-1[ i t]， t=1，2，…，N-1

程序后

其中：n表示算法中使用的一个字节长度;N表示长度为n的一个字节能显示值的总量，即N=2n; i t和 j t表示两个参数;K表示种子密钥，l为其长度，l=K的比特数/n。

1.2 伪随机序列生成算法PRGA

PRGA生成的伪随机序列构成加解密运算的密钥流序列。伪随机序列生成原理如图2所示。

PRGA[17-18]的步骤如下：

步骤1  初始化。指针 i t和 j t的初始值在KSA产生的S0中选取。

步骤2  变换S盒。改变该算法中的j值，并将St中的 i t和 j t进行交换。

步骤3  生成伪随机序列Z。连续改变S盒中各个字节的位置，并输出变换后的St[ i t]+St[ j t]位置的值，该输出字节序列是伪随机序列，也是密钥流序列，记为Z={Zt}∞t=0，加密时，用Zt与明文进行异或运算，解密时同样用Zt与密文进行异或运算。

RC4的PRGA伪代码如下：

程序前

PRGA： i 0=0，  j 0=0; i t= i t-1+1;

St-1[ j t]= j t-1+St-1[ i t];

St[ i t]=St-1[ j t]， St[ j t]=St-1[ i t];

Zt=St[St[ i t]+St[ j t]]， t=1，2，…，N-1

程序后

其中： i t，  j t表示两个位置参数，Zt表示t时刻的输出值。加密时，将Zt与明文异或;解密时，将Zt与密文异或。

2 改进的RC4算法

针对原有RC4算法密钥流序列随机性不高、易受区分攻击、“受戒礼”攻击和状态猜测攻击等问题，提出了基于椭圆曲线的改进RC4算法。该改进算法利用椭圆曲线、MD5哈希算法和伪随机数产生器，在随机性、安全性等方面有较大的提升。椭圆曲线固有的数学困难问题、不易破解，MD5哈希算法存在单向安全性以及伪随机数产生器的随机性，增加了RC4算法密钥流序列的随机性，增强了改进算法的安全性，可以有效抵抗区分攻击、“受戒礼”攻击和状态猜测攻击。

基于椭圆曲线的改进RC4算法利用椭圆曲线产生单向不可逆的整数，经MD5哈希算法生成消息摘要后送入伪随机数产生器生成伪随机数，在S盒中进行非线性变换最后生成用于加解密的密钥流序列。

改进RC4算法由密钥编制算法KSA和伪随机序列生成算法PRGA两部分组成，流程如图3所示，步骤如下：

步骤1  产生随机整数e。随机取五位大素数p通过椭圆曲线y2=x3+x+1产生随机整数e。

步骤2  变换随机整数e。借助MD5哈希算法将随机整数e以128bit输出。

步骤3  产生密钥Key。 从产生的128bit数据中选取一个64bit的随机数送入伪随机数产生器，输出新的64bit的伪随机数Ri作为密钥Key。

步骤4  初始化S盒。N步遍历后产生RC4的初始状态S0。根据初始状态表，初始化指针 i t和 j t。

步骤5  产生密钥流序列。更新指针 i t和 j t进行非线性变换，不断改变S盒中元素的位置，每次改变后将St[ i t]+St[ j t]位置的值Z输出，即伪随机序列，也称密钥流序列。

算法的时间复杂度为O（n2）。

3 改进RC4的密钥编制算法KSA

椭圆曲线加密（Elliptic Curve Cryptography， ECC）算法[19-20]是一类以椭圆曲线的数学理论为核心的单向不可逆公钥密码体制，优点是密钥短、安全性高且存储空间小，其安全性主要依据由其定义的某类椭圆曲线点群上的离散对数问题求解的困难性，椭圆曲线密码系统单位比特的高强度使得椭圆曲线密码体制成为目前信息安全领域的核心体制。本文提出的基于椭圆曲线的RC4改进算法的密钥编制算法KSA分为以下3个部分。

3.1 利用椭圆曲线生成随机整数

密码学中普遍采用的是有限域上的椭圆曲线，即所有系数都是某一有限域GF（p）中的元素（其中p为一个大素数）。其中最常用的是由方程

y2=x3+ax+b （a，b∈GF（p），4a3+27b2≠0）

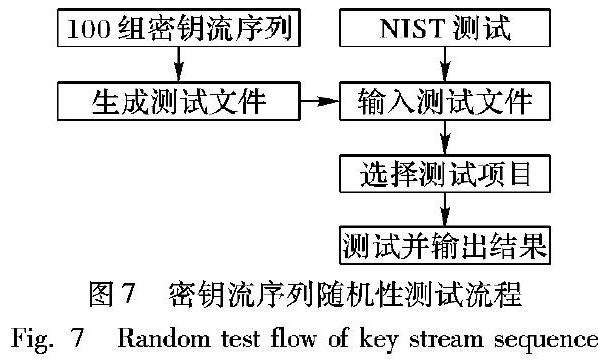
定义的曲线。本文取a=1，b=1，即方程y2=x3+x+1进行运算，其图形是连续曲线，如图4所示，设EP（1，1）表示方程y2=x3+x+1所定义的椭圆曲线上的点集{（x，y） | 0≤x

步骤1  对每一x（0≤x

步骤2  判断步骤1中求得的模p下是否有平方根：如果没有，则曲线上不存在与该x相对应的点;如果有，则求出两个平方根（y=0时只有一个平方根）。

按照上述方式，GF（p）上的椭圆曲线y2=x3+x+1在第一象限的整数点加无穷远点O共有1+p+∑ x∈GF（p）   x3+x+1 p  个。本文取p为五位随机大素数进行运算，从生成的点集EP（1，1）中去掉x=0，y=0和无穷远点，在剩下的点集中随机取一个坐标点，这个坐标点的y坐标的值即为所需要的整数，记为e，进行接下来的运算。

3.2 利用哈希函数生成消息摘要

哈希函数是密码学的重要内容，将任意长的消息M映射为较短的、固定长度的一个值H（M），即消息摘要（又称为哈希码）。哈希函数满足单向性的特点，即它只可从明文得到密文而不可从密文获得明文，只有加密过程，不能解密[21]。

本文采用MD5哈希算法对数据进行处理，MD5采用迭代型哈希函数结构，算法框图如图5所示，算法的输入为任意长消息（图中为Kbit），实际运行时将输入3.1节中生成的整数e分成512bit长的分组，输出为128bit的消息摘要。

由图5可知，MD5算法对输入数据的处理过程如下：

步骤1  对输入的Kbit消息进行填充，使得e的比特长在模512下为448，留出的64bit给步骤2使用。

小端方式：指将数据的低位放在内存的低地址上，而数据的高位放在内存的高地址上。

步骤2  附加消息的长度，用步骤1留出的64bit以小端方式表示消息被填充前的长度，如果消息长大于264，则以264为模数取模。

步骤3  对MD5缓冲区初始化。

步骤4  以分组为单位对消息进行处理。

步骤5  输出。消息的L个分组都被处理完后，最后一个HMD5的输出即为需要的128bit的消息摘要。

3.3 利用伪随机数产生器产生伪随机数

从3.2节产生的128bit的消息摘要中选取64bit的随机数n送入伪随机数产生器，输出新的64bit的伪随机数Ri送入S盒，经过N步遍历生成RC4的初始状态S0。由图6产生器的框图可知，产生器的运行分为3个部分：

步骤1  输入两个64bit的伪随机数，其中DTi表示当前的日期和时间，每产生一个数Ri后，DTi都更新一次;Vi是产生第i个随机数时的种子，初值可以任意设定，这里设为随机数n，以后每次自动更新。

步骤2  密钥。产生器用了3次三重DES加密，3次加密使用相同的两个56bit的密钥K1和K2，这两个密钥必须保密且不能用作他用。

步骤3  输出。输出为一个64bit的伪随机数Ri和一个64bit的新种子Vi+1，其中：

Ri=EDEK1，K2[Vi⊕EDEK1，K2[DTi]]

Vi+1=EDEK1，K2[Ri⊕EDEK1，K2[DTi]]

EDE表示两个密钥的三重DES。

4 改进RC4算法安全性分析

密钥流序列的随机性是指密钥流中各比特之间具有的独立程度。提高密钥流的独立性，将会增大密文的统计分析的难度，攻击者难以破解。因此，提高密钥流的独立性（即随机性）是衡量流密码安全性的重要指标之一。RC4算法近年频遭攻击，其中最典型的包括区分攻击、“受戒礼”攻击和状态猜测攻击，本文针对这三类攻击对改进RC4算法进行安全性分析。

索引指针只表示位置，不作为向量，it即表示位置又表示值时才视为向量

4.1 密钥流序列的随机性

影响RC4算法的密钥流序列随机性的三个因素包括：1）S盒中的初始值分布均匀程度;2）索引指针i， j分布均匀程度;3）根据指针输出的结果分布均匀程度。RC4算法的内部状态由一个包含256Byte的S盒和指针i， j组成，输出的密钥流序列由S盒中的初始值和指针i， j共同确定，因此输出不重复的值至多Z82个，范围较小，密钥流序列的随机性较差。

1）理论验证改进RC4算法的密钥流序列随机性。

RC4算法的S盒中的初始值由初始密钥Key和指针确定，改进RC4算法中，密钥Key的产生由以下三部分确定：

①椭圆曲线y2=x3+x+1。由图4可知该曲线平滑连续，函数值分布均匀。

②MD5哈希算法。该算法采用迭代型哈希函数结构，将输入的消息填充后划分为一系列512bit长的分组Y0，Y1，…，YL-1对消息进行处理，每一分组Yq（q=0，1，…，L-1）都经压缩函数HMD5处理，算法采用128bit长的缓冲区存储中间结果和最终哈希值，使得消息具有安全性且分布均匀。

③伪随机数产生器。哈希函数生成的均匀分布的128bit数据随机取64bit送入伪随机数生成器，产生器采用112bit长的密钥和3次三重DES加密，生成的随机数Ri随机性很高，送入S盒后进行非线性变换，使得S盒初始值分布均匀。而在伪随机序列生成过程中，由于S盒中256个元素是均匀分布的，S[i]中的值和指针i， j分布均匀，所以算法的输出密钥流序列（S[i]+S[j]） mod 256也分布均匀。

内部状态分布均匀，产生的值均为随机数，改进算法的密钥流序列随机性高于RC4算法。

2）实验验证改进RC4算法的密钥流序列随机性。

本文密钥流序列的随机性测试采用美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）提供的NIST統计测试套件[22]完成，Linux操作系统因其完备的功能、强大的性能、良好的兼容性以及开源免费等优点，本文采用Linux虚拟环境对RC4算法和改进RC4算法的密钥流序列进行测试[23]。测试中，取显著性水平α=0.01，取256Byte内的密钥，分别输出两种算法的密钥流序列1048576bit，更换随机密钥，产生100 组序列进行测试，密钥流序列随机性测试流程如图7所示。步骤如下：

步骤1  产生100组密钥流序列。将椭圆曲线、MD5算法和伪随机数产生器产生的随机数经过S盒变换生成一组密钥流序列，共循环产生100组。

步骤2  生成测试文件。将步骤1中产生的100组密钥流序列以ASCII或二进制形式保存在测试文件中。

步骤3  启动NIST测试平台导入测试文件。在Linux环境下，启动NIST测试平台，配置参数，并导入步骤2中产生的测试文件。

步骤4  选择测试项目，输入参数后开始测试。在NIST平台中选择频率检验、游程检验、序列检验等16项随机性测试项目，并输入相关参数开始测试。

步骤5  查看测试结果进行分析。

RC4算法与改进RC4算法密钥流序列随机性测试结果如表1所示。

表1中p-value是利用卡方分布进行统计分布均匀性的一种指标，测试结果表明，RC4算法和改进RC4算法的密钥流序列虽然都能够通过测试，但改进RC4算法检测结果均高于RC4算法，特别是最重要的三项测试[24]：频率检验、游程检验和Maurer的通用统计检验的结果比RC4算法分别高出0.13893，0.13081，0.232050。因此，本文改进的RC4算法产生的密钥流序列比原RC4算法的独立性高，随机性和安全性均优于RC4算法。

4.2 抵抗区分攻击

由于KSA生成的密钥流序列可能存在偏差，区分攻击就是指对该偏差进行的攻击。

文献[8]证明了RC4算法在KSA部分所得的内部状态分布不均，文献[4]证明了根据RC4密钥流前两个输出字节存在的偏差进行区分攻击只需要226Byte即可恢复RC4算法的初始状态S0。文献[6]证明了密钥流的第1个输出字节分布不均匀，区分攻击只要224Byte即可恢复初始状态S0。而在本文的改进RC4算法中，KSA部分所得的内部状态分布均匀，不存在这些偏差，因此这些攻击无效。

RC4算法区分攻击的原理如下：

定理1  记P（SN[u]=v）为RC4 算法在经过KSA 后，数组SN输入为u、输出为v的概率[5]，为保证数据不存在偏差，其计算条件为i=0， j=j+S[i]，Swap（S[i]，S[j]）：

1）当u+1≤v≤N-1时，有：

P（SN[u]=v）=pu，vv+1·  N-1 N  N-1-v+

（1-pu，vv+1）· 1 N ·   N-1 N  v-  N-1 N  N-1

其中：

pu，vv+1=

2（N-1） N2 ，       u=0，v=1

1 N ·  N-1 N  v-u+ 1 N ·  N-1 N  v- 1 N2 ·  N-1 N  2v-u-1， 其他

2）当v≤u≤N-1时，有：

P（SN[u]=v）= 1 N ·  N-1 N  N-1-u+    1 N ·   N-1 N  v+1-  N-1 N  N+v+u

设P（SN[0]=x）为数组SN输入为0输出为x的概率，P（SN[x]=y）为数组SN输入为x、输出为y的概率，P（SN[z]=m）为数组SN输入为z、输出为m的概率，其中，z=（x+y） mod 256，则可得密钥流输出的第1 个密钥字为一特定值的概率。

定理2  RC4 算法密钥流输出的第1个字节Z1的概率为：

P（Z1=m）=∑ x ∑ y P（SN[0]=x）·  P（SN[x]=y）·P（SN[（x+y） mod 256]=m）

对于所有的m（0≤m≤255），根据定理1和定理2可以计算出P（Z1=m），即理论值Pm。文献[10]利用232个随机密钥产生RC4密钥流的第一个字节进行统计，得到了理论值和实验值结果相同。可见，对于RC4算法的区分攻击只是时间问题，RC4的初始状态S0总是会被恢复的。

本文改进的RC4算法抵抗区分攻击分为两方面：

1）本文改进的RC4算法中，产生的密钥流序列由Key、指针S[i]、S[j]共同确定，由于Key是一个秘密生成的随机数且分布均匀，前两个输出字节不存在偏差问题，因此不存在定理1中计算条件问题;另外，改进RC4算法的Key具有秘密随机的特性，定理1、2中数组SN输入固定值、输出固定值的概率不能确定，第一个输出字为一特定值的概率不能计算，定理1、2不适用于改进RC4算法。

2）改进RC4算法的密钥流序列的随机性高于RC4算法，对改进RC4算法的区分攻击所需要字节数高于RC4算法，耗时长于RC4算法，但密钥流序列具有时效性，在有效时长内区分攻击无法对改进RC4算法进行有效攻击，因此区分攻击的攻击方法对改进RC4算法是无效的，即改进RC4算法能够有效抵抗区分攻击。

4.3 抵抗“受戒礼”攻击

“受戒礼”攻击是指利用不变性弱密钥进行的攻击，攻击者通过嗅探监听大量的SSL链接，判断出第一个加密消息包含SSL的完成消息和HTTP请求的可预测的信息，当等到一个不变性弱密钥的链接时，一旦明文和这个弱密钥进行异或，攻击者就可以看到生成的密文模式，异或后可获得相应的明文。

改进RC4算法中，密钥流序列由Key和指针共同确定。其中，Key由椭圆曲线、哈希函数和伪随机数产生器共同确定。椭圆曲线根据随机素数生成的随机整数送入MD5哈希算法后随机取64bit作为产生器的第一个种子，产生器的两个输入为当前的日期、时间和算法上次产生的新种子，密钥流序列不断变化，信息随机性变换，攻击者很难获得可预测信息，不存在不变性弱密钥，改进RC4算法可有效抵抗“受戒礼”攻击。

文献[9]中分析了RC4算法中KSA的输出值，发现不变性弱密钥是一个L型图案，这部分密钥可能表现出非随机的特性，攻击者根据这些特性探测出完整密钥从而进行攻击。对状态表S盒中元素进行统计分析可知，KSA执行结束时状态表S中X值出现在位置Y的概率是：

P[S0[Y]=X]= p（qX+qY′-qX+Y′），  X≤Yp（pX+qY′）， X>Y

其中：Y′=N-1-Y，p=1/256，q=1-p。尤其是值1和值255出现在0位置的概率分别比随机概率1/N高37%、低26%。攻击者对获得的统计值进行分析，并结合N轮计算后的PRGA，也可以恢复密钥。

在改进的RC4算法中，上述问题很难发生。满足P[S0[Y]=X]的条件是：1）若X=Si[1]且Y=Si[X]则i>1，i≥X，i≥X+Y，其中i时刻S[X]的状态用Si[X]表示。2）攻击者必须知道S[1]、S[X]和S[X+Y]的值。改进RC4算法对KSA部分进行改进，椭圆曲线的离散对数问题使得椭圆曲线单向不可逆，经过MD5和伪随机数产生器进一步处理，Key无法被破解，S盒的初始值无法被获取。即使获得了初始值，初始S盒的元素每一次都是随机产生，跟初始值无关且不同，i≥1时的下一次迭代后的状态和S[1]的值也无法获知，因此不满足上述概率，密钥无法恢复。所以“受戒礼”攻击对改进RC4算法无效，即改进RC4算法可以抵抗“受戒礼”攻击。

4.4 抵抗状态猜测攻击

文献[7]中针对RC4算法中的PRGA部分進行状态猜测攻击，假设攻击者获得了一段足够多的PRGA 输出值对内部状态赋值，根据已知的输出值和其他信息进行判断，如果矛盾，重新赋值;如果整个赋值过程中没有矛盾，攻击者即得到一个正确的内部状态。若攻击者能够根据这些输出值计算出PRGA 的初始状态，那么无需密钥即可以继续产生任何输出值，RC4 算法即被破解。

在改進RC4算法中，KSA部分借助伪随机产生器使得初始Key不断改变，S盒的初值即PRGA的初始状态也随之改变，攻击者对PRGA状态赋值成功后得到的内部状态也已失效，无法继续产生输出值。同时改进RC4算法的KSA部分使得Key随机性很高，很难赋值成功，且密钥生存期很短，攻击者获知初始状态进行猜测花费的时间高于密钥生存期，赋值成功得到的信息失去时效性，攻击失败。因此，改进RC4算法可以抵抗状态猜测攻击。

状态猜测攻击过程如图8所示，其步骤如下：

步骤1  根据Have_val值（TRUE或FALSE）判断St-1[ i t]是否被赋值。

①已赋值，则转步骤2。

②若未赋值，则从2n-a选出一个未使用值对St[ i t]赋值，更新at，得到 j t= j t-1+St-1[ i t]，转步骤2。

步骤2  判断Zt是否与at中某值相等。

①若相等，计算St-1[ j t]=S-St[Zt]-St-1[ j t]，判断St-1[ j t]是否已被赋值过;若是，判断是否与计算值相等，相等则t=TRUE，转步骤1;不相等则返回步骤1的②，重新对St-1[ j t]赋值。若Have_val=FALSE，判断刚计算的St-1[ j t]是否在at中：若不存在，用刚计算出的St-1[ j t]赋值，更新at，返回步骤1;若存在，返回步骤1的②，对St-1[ i t]赋值。

②若不相等，则转步骤3。

步骤3  根据Have_val值（TRUE或FALSE）判断St-1[ j t]是否被赋值。

①若未赋值，则从2n-a选出一个未使用值对St-1[ j t]赋值，更新at，计算 i t=St-1[ i t]+St-1[ j t]，判断St[ i t]是否被赋值：若被赋值，判断是否等于Zt，相等则t=TRUE，转步骤1;不相等则重新对St-1[ j t]赋值。

若未被赋值，判断Zt是否出现在at中：若存在则重新赋值St-1[ j t];若不存在则用Zt值更新St[ i t]，更新at值，令t=t+1，返回步骤1。

若Zt对St[ i t]中所有值的赋值均出现矛盾，则返回步骤1的①，重新对St-1[ i t]赋值。

②若已赋值，则计算 i t=St-1[ i t]+St-1[ j t]，判断是否被赋值：若未被赋值，则把Zt赋值给St[ i t]，更新at，令t=t+1，返回步骤1;若已被赋值，则出现矛盾返回步骤1的②，再次对St-1[ i t]赋值。

其中：S-1t[Zt]表示输出值Zt在内部状态S中的对应位置; j t，St[ i t]，St[ j t]分别为t时刻j，S[i]，S[j]的值;at为已猜测出的字节。从状态猜测攻击的攻击过程看出，猜测过程中主要是猜测 j t，St[ i t]，St[ j t]和S-1t[Zt]直到t=0时S0中的所有算法。已获知的初始状态越少，复杂度越高，需要进行的猜测越多，攻击越困难，算法越安全。

对于初始状态表S0猜测成功一般应该存在以下两个条件：

1）已获得四个未知数中的三个，猜测第四个，如若已知 j t，St[ i t]，St[ j t]和S-1t[Zt]且Zt已在状态表S中被赋值，则St[ j t]=S-1t[Zt]-St[ i t]。

2）S盒中的元素取值是固定范围，且St-1[ i t]或St-1[ j t]每一次都必须与S中已经赋过的值不同。

而在改进RC4算法中，椭圆曲线、MD5哈希函数和伪随机数产生器无法被破解，攻击者无法获知t时刻的内部状态，即无法获知四个未知数中的任意三个，条件1）无法满足;S盒中元素取值范围影响因素包括：①随机大素数p，②椭圆曲线y2=x3+x+1，③MD5哈希函数，④伪随机数产生器，四个因素，高随机性使得S盒中元素取值不会是固定范围，条件2）失效。因此状态猜测攻击无法攻击改进RC4算法，即改进的RC4算法可以有效抵抗状态猜测攻击。

5  结语

本文提出了一种基于椭圆曲线的改进RC4算法，该算法通过椭圆曲线、哈希函数和伪随机数产生器生成初始密钥Key，在S盒和指针的作用下进行非线性变换最终生成了随机性和安全性很高的密钥流序列。该密钥流序列由随机产生的初始Key、大素数和指针i、  j共同确定，利用NIST随机性测试工具对密钥流序列在频率检验、游程检验和Maurer等16个指标进行检测，结果表明，该3项指标改进的RC4算法比原RC4算法分别高出0.13893，0.13081，0.232050，因此，该算法密钥流随机性高于RC4算法，能够有效防止不变性弱密钥的产生，能够抵抗“受戒礼”攻击。Key是一个分布均匀的随机数，不存在偏差，能够有效抵御区分攻击。椭圆曲线、哈希函数具有单向不可逆性，伪随机数产生器具有高密码强度，Key猜测赋值困难，能够抵抗状态猜测攻击。安全性理论分析和随机性实验结果表明，改进RC4算法的安全性和随机性高于RC4算法。本文在错误引入攻击和明文恢复攻击等方面未进行有效测试和验证，这些将是下一步的研究方向。

参考文献

[1]   FINNEY H. An RC4 cycle that cant happen [J]. Post. in Sci.  Crypt.，1994： 246.

[2] KNUDSEN L R， MEIER W， PRENEEL B， et al. Analysis methods for （alleged） RC4 [C]// Proceedings of the 1998 International Conference on the Theory and Application of Cryptology and Information Security， LNCS 1514. Berlin： Springer， 1998： 327-341.

[3] FLUHRER S R， McGREW D A. Statistical analysis of the alleged RC4 keystream generator [C]// Proceedings of the 2000 International Workshop on Fast Software Encryption， LNCS 1978. Berlin： Springer， 2000： 19-30.

[4] PAUL S， PRENEEL B. A new weakness in the RC4 key stream generator and an approach to improve the security of the cipher [C]// Proceedings of the 2004 International Workshop on Fast Software Encryption， LNCS 3017. Berlin： Springer， 2004： 245-259.

[5] MIYAJI A， SUKEGAWA M. New analysis based on correlations of RC4 PRGA with nonzero-bit differences [J]. IEICE Transactions on Fundamentals of Electronics， Communications and Computer Sciences， 2010， E93-A（6）： 1066-1077.

[6] 常亞琴.对流密码RC4的区分攻击[J].计算机工程，2011，37（3）：119-120，123. （CHANG Y Q. Distinguishing attack on stream cipher RC4 [J]. Computer Engineering， 2011， 37（3）： 119-120， 123.）

[7] HOCH J J， SHAMIR A. Fault analysis of stream ciphers [C]// Proceedings of the 2004 International Workshop on Cryptographic Hardware and Embedded Systems， LNCS 3156. Berlin： Springer， 2004： 240-253.

[8] FLUHRER S， MANTIN I， SHAMIR A. Weakness in the key scheduling algorithm of RC4 [C]// Proceedings of the 2001 International Workshop on Selected Areas in Cryptography， LNCS 2259. Berlin： Springer， 2001： 1-24.

[9] MANTIN I. Analysis of the stream cipher RC4 [D/OL]. Weizmann Institute of Science， 2001 [2018-10-23]. http： //www.wisdom.weizmann.ac.il/itsik/RC4/Papers/Mantin1.zip.

[10] AKGN M， KAVAK P， DEMIRCI H. New results on the key scheduling algorithm of RC4 [C]// Proceedings of the 2008 International Conference on Cryptology in India， LNCS 5365. Berlin： Springer， 2008： 40-52.

[11]  MANTIN I. Bar-Minzva attack： breaking SSL with 13-year old  RC4 weakness [N]. Blackhat， 2015-03-22.

[12] 苑超，徐蜜雪，斯雪明.对不同种子密钥长度的RC4算法的明文恢复攻击[J].计算机应用，2018，38（2）：370-373. （YUAN C， XU M X， SI X M. Plaintext recovery attack on RC4 with different length of seed key [J]. Journal of Computer Applications， 2018， 38（2）： 370-373.）

[13] 胡亮，迟令，袁巍，等.RC4算法的密码分析与改进[J].吉林大学学报（理学版），2012，50（3）：511-516. （HU L， CHI L， YUAN W， et al. Cryptanalysis and improvements of RC4 algorithm [J]. Journal of Jilin University （Science Edition）， 2012， 50（3）： 511-516.）

[14] 陈立，邓成良，肖慧娟.基于RC4的混沌改进算法及其性能分析[J].科学技术与工程，2010，10（26）：6449-6452，6458. （CHEN L， DENG C L， XIAO H J. An algorithm improved by chaos based on RC4 and its performance analysis [J]. Science Technology and Engineering， 2010， 10（26）： 6449-6452， 6458.）

[15] ZOLTAK B. VMPC oneway function and stream cipher [C]// Proceedings of the 2004 International Workshop on Fast Software Encryption， LNCS 3017. Berlin： Springer， 2004： 210-225.

[16] TSUNOO Y， SAITO T， KUBO H， et al. The most efficient distinguishing attack on VMPC and RC4A [J]. Estream Project， 2005： 1-12. 沒找到

[17] 侯整风，孟毛广，朱晓玲，等. RC4流密码算法的分析与改进[J].计算机工程与应用，2015，51（24）：97-101. （HOU Z F， MENG M G， ZHU X L， et al. Analysis and improvement of RC4 stream cipher algorithm [J]. Computer Engineering and Applications， 2015， 51（24）： 97-101.）

[18] 孟毛广.RC4流密码算法的研究与改进[D].合肥：合肥工业大学，2014：9-12. （MENG M G. Research and improvement of RC4 stream cipher algorithm [D]. Hefei： Hefei University of Technology， 2014： 9-12.）

[19] 田松，李宝，王鲲鹏.椭圆曲线离散对数问题的研究进展[J].密码学报，2015，2（2）：177-188. （TIAN S， LI B， WANG K P. On the progress of elliptic curve discrete logarithm problem [J]. Journal of Cryptologic Research， 2015， 2（2）：177-188.）

[20] 张小红，郭焰辉.基于椭圆曲线密码的RFID系统安全认证协议研究[J].信息网络安全，2018，18（10）：51-61. （ZHANG X H， GUO Y H. Research on RFID system security authentication protocol based on elliptic curve cryptography [J]. Netinfo Security， 2018， 18（10）： 51-61.）

[21] 巫光福，曾宪文，刘娟，等.基于纠错码的Hash函数的设计与分析[J].信息网络安全，2018，18（1）：67-72. （WU G F， ZENG X W， LIU J， et al. Design and analysis of hash function based on error correcting code [J]. Netinfo Security， 2018， 18（1）： 67-72.）

[22] BARKER E， BARKER W， BURR W， et al. Recommendation for Key Management — Part 1： General， SP 800-57 [R]. Gaithersburg， MD： National Institute of Standards & Technology， 2007： 1-142.

[23] 翟高寿，刘晨，向勇.基于内核函数监控的Linux系统防护方法的研究与实现[J].信息网络安全，2018，18（3）：26-38. （ZHAI G S， LIU C， XIANG Y. Study and implementation of systematic protection by monitoring abnormal invocation of Linux kernel functions [J]. Netinfo Security， 2018， 18（3）： 26-38.）

[24] KIM S， UMENO K， HASEGAWA A. Corrections of the NIST statistical test suite for randomness [EB/OL]. [2018-10-10]. http： //www.docin.com/p-1036631337.html.