基于凸边界的学习样本抽取方法

顾依依 谈询滔 袁玉波

摘 要： 學习样本的质量和数量对于智能数据分类系统至关重要，但在数据分类系统中没有一个通用的良好方法用于发现有意义的样本。以此为动机，提出数据集合凸边界的概念，给出了快速发现有意义样本集合的方法。首先，利用箱型函数对学习样本集合中的异常和特征不全样本进行清洗;接着，提出数据锥的概念，对归一化的学习样本进行锥形分割;最后，对每个锥形样本子集进行中心化，以凸边界为基础提取距离凸边界差异极小的样本构成凸边界样本集合。实验在12个UCI数据集上进行，并与高斯朴素贝叶斯（GNB）、决策树（CART）、线性判别分析（LDA）、提升算法（AdaBoost）、随机森林（RF）和逻辑回归（LR）这六种经典的数据分类算法进行对比。结果表明，各个算法在凸边界样本集合的训练时间显著缩短，同时保持了分类性能。特别地，对包含噪声数据较多的数据集，如剖腹产、电网稳定性、汽车评估等数据集，凸边界样本集合能使分类性能得到提升。为了更好地评价凸边界样本集合的效率，以样本变化率和分类性能变化率的比值定义了样本清洗效率，并用该指标来客观评价凸边界样本的意义。清洗效率大于1时说明方法有效，且数值越高效果越好。在脉冲星数据集合上，所提方法对GNB算法的清洗效率超过68，说明所提方法性能优越。

关键词：机器学习;数据分类;样本选择;凸锥;边界样本

中图分类号： TP311.1

文献标志码：A

Learning sample extraction method based on convex boundary

GU Yiyi， TAN Xuntao， YUAN Yubo*

School of Information Science and Engineering， East China University of Science and Technology， Shanghai 200237， China

Abstract： The quality and quantity of learning samples are very important for intelligent data classification systems. But there is no general good method for finding meaningful samples in data classification systems. For this reason， the concept of convex boundary of dataset was proposed， and a fast method of discovering meaningful sample set was given. Firstly， abnormal and incomplete samples in the learning sample set were cleaned by box-plot function. Secondly， the concept of data cone was proposed to divide the normalized learning samples into cones. Finally， each cone of sample subset was centralized， and based on convex boundary， samples with very small difference from convex boundary were extracted to form convex boundary sample set. In the experiments， 6 classical data classification algorithms， including Gaussian Naive Bayes （GNB）， Classification And Regression Tree （CART）， Linear Discriminant Analysis （LDA）， Adaptive Boosting （AdaBoost）， Random Forest （RF） and Logistic Regression （LR）， were tested on 12 UCI datasets. The results show that convex boundary sample sets can significantly shorten the training time of each algorithm while maintaining the classification performance. In particular， for datasets with many noise data such as caesarian section， electrical grid， car evaluation datasets， convex boundary sample set can improve the classification performance. In order to better evaluate the efficiency of convex boundary sample set， the sample cleaning efficiency was defined as the quotient of sample size change rate and classification performance change rate. With this index， the significance of convex boundary samples was evaluated objectively. Cleaning efficiency greater than 1 proves that the method is effective. The higher the numerical value， the better the effect of using convex boundary samples as learning samples. For example， on the dataset of HTRU2， the cleaning efficiency of the proposed method for GNB algorithm is over 68， which proves the strong performance of this method.

Key words： machine learning; data classification; sample selection; convex cone; boundary sample

0 引言

随着社会的进步，尤其是服务业的蓬勃发展，从数据中获取有用信息的需求急剧增长。而数据分类是一个重要的挑战，一个好的分类系统对该行业的发展至关重要。例如，餐饮业可以根据历史消费记录对顾客进行分类，给不同类别的顾客相应的优惠待遇，并推荐合适的菜肴;保险公司可以根据家庭基本信息对家庭情况进行分类，从而推荐合适的保险，既能满足用户的自身需求，又能提高公司的效益。分类系统的核心是分类模型的选择和构建，训练集将参与到具体分类模型的构建过程中。因此，训练集的质量将很大程度上影响模型的预测效果，训练样本对分类系统非常重要。

基于真实世界中海量数据的原因，如果系统直接将某行业内产生的所有数据作为训练集，将会导致工作负载超重、资源浪费、处理速度慢等状况;并且来源于真实世界中的数据集通常包含缺失数据、异常数据和大量冗余数据，这将会降低训练集的质量，从而降低数据分类的效率。为了提高训练集的质量，需要一种样本选择方法来选择具有代表性的样本，这些选择到的样本可以代表原始数据集所包含的信息及其数据分布特征。并且，使用所选的代表性样本作为训练集可以减小内存开销和降低分类模型的复杂度，从而加快建模速度。用于发现具有代表性样本的样本选择方法

可以很好地处理因社会快速发展而产生的海量数据。

本文提出了边界样本的概念。事实上，它们是构建分类模型的关键样本，起着决定性的作用。对于分类任务，决策边界附近的样本最容易被误分类，它们是最模糊的、有歧义的;但它们往往也包含更丰富的信息。本文提到的边界样本就是具有这种特性的样本。本文通过数据锥的概念来发现它们，从而替代通过决策边界找到这些样本的方法。更具體地说，边界样本类似于支持向量机（Support Vector Machine， SVM）[1]中的支持向量。因此，本文所设计的方法是选择边界样本。

本文主要工作有：1）提出了边界样本的概念，这些样本对分类模型的构建起着决定性的作用;2）采用数据锥的概念对子集进行划分，选择边界样本;3）给出了效率分析公式，使用训练样本集大小的比值与其对应分类准确率的比值来综合分析该方法的可行性。

1 相关工作

对于分类性能的提升，一是针对训练集进行处理，二是对分类模型进行设计或改进其性能。如今，已经有非常多的流行技术，也不断涌现出各种新兴技术。

随着数据量的急剧增长，并且时间和人工越来越宝贵，许多研究开始关注于样本冗余和去重。它们的目标是减少计算量及人工标记开销，并且尽可能地提高机器学习的准确率。对于训练集的处理，主要有两方面：样本约简和维度约简。样本约简，即样本选择，通常分为数据压缩和积极学习两大类，其中可以使用有监督、半监督、无监督策略。

有监督和无监督依赖于专家人工完成样本选择和去重的工作;而半监督，如积极学习，可以减少人工标注的开销。

现在已经有许多有效的样本选择和去重方法：如文献[2]中提出了一种遗传编程的方法来删除重复记录，它结合了从数据中提出的几个不同的片段，以此为依据在库中识别两个条目是否为重复数据;

文献[3]中提出了一种新的框架FS-Dedup（Framework for Signature-based Deduplication），其技术核心是基于签名的重复数据删除，

在去重的工作中减轻了人工开销，仅需标记一个小的匹配对子集;文献[4]在文献[3]的基础上进行了改进，提出了一种两阶段抽样选择策略T3S（two-stage sampling selection），在第二阶段中迭代地进行主动选择，从而去除第一阶段中所得到的子集的中的冗余数据。以上几种研究都是通用的样本去重方法，不针对特定分类模型，在文献[5-8] 中所提出的样本选择方法主要针对决策树、神经网络及支持向量机。文献[5]中提出了一种在模糊决策树中根据最大歧义性来选择样本的方法。文献[6]中将K-最近邻分类算法中的数据约简技术应用于神经网络和支持向量机之前的预处理步骤。

数据约简技术就是试图通过选择一些现有实例或生成新的训练实例来减小训练集的大小。支持向量机对于小样本的分类任务效果出众，但当样本量增加，达到数十万的中等问题规模时，训练的时间和内存需求激增。针对这一问题，文献[7]中基于聚类的SVM模型进一步探究每个聚成的簇里的聚集点和离散点，其中，聚集点被认为不含支持向量从而被去除，保留包含支持向量的离散点。并且文献[7]中利用Fisher判别比来确定每一个簇里聚集点和离散点之间的边距，边界的确定是基于计算数据点到簇中心的距离。

本文所设计的样本选择方法则希望可以应用于多种分类器，不受分类器种类不同的影响，在加快训练速度和减少内存开销的同时，保持准确率的不变或小幅下降。

文献[8]中介绍了一种针对SVM处理大规模数据集时间长、泛化能力下降等问题的边界样本选择方法，通过K均值聚类后，在每个簇中通过K近邻算法剔除非边界样本以得到边界样本集。但此方法先要进行K均值聚类，对于K的选择有很大的不确定性;并且需要再通过一个K近邻算法剔除非边界样本，增加了方法的复杂度;而且只针对于SVM分类器。而本文选择的凸边界样本集无需调用其他算法，且设计目标是适用于多种分类模型。

提升分类性能的预处理过程中，还有另一项重要的工作——维度约简，即特征选择。数据集维数急剧增加，特征选择成为机器学习的必要步骤。

文献[9]在分类任务的背景下，从理论和实验的角度研究了现有特征选择技术之间的相似性，并且当多个特征选择方法组合时，对于所考虑的任务目标能够给出不同或互补的表示时才是有益的。

文献[10]提出了一种基于类可分性策略和数据包络分析的特征选择方法，将类标签作为单独的变量，在每个类标签上处理相关性和冗余;并使用超效率数据包络分析计算特征在类标签上的得分，选择最大得分的特征加入下一轮迭代的条件集中，不断迭代地选择最终的特征。本文的样本选择方法也采取了在每个类标签上处理数据的方法，从而进行边界样本的选择。文献[11]使用了集成的思想进行特征选择能获得更好的分类性能。

在具体的分类任务中，经常会遇到不平衡分类数据的问题，即分类结果会倾向于多数群体，使得少数类被误分。因此，现有许多研究都在致力于解决不平衡数据分类问题，提高分类模型的精度。文献[12]中提出了一种改进基于先验的综合过采样方法来提高不平衡数据集的分类灵敏度。分类模型的估计不仅受类分布的倾斜影响，而且由于数据的稀缺性导致对模型精度的估计较差。文献[13]基于平滑自助重采样技术，提出了一个统一的系统框架来处理类分布的倾斜影响和数据的稀缺性。

通常，K折验证技术可使不同分区的结果具有一定程度的独立性，但每个折叠上的随机划分会导致训练子集和测试子集之间具有不同的数据分布导致数据位移的问题，尤其是在不平衡分类数据集中更加严重，从而导致对实际分类边界的错误学习，使少数类实例被误分。文献[14]中提出了分布最佳平衡分层交叉验证的方法，

首先使用一种特定的技术对数据进行分区，并通过在不同的交叉验证折叠上设置每个分区上数量相近的样本，以避免随机划分所产生的不平衡分类的影响。

除了以上几种方法以外，文献[15]提出了一种模糊神经算法，目的是最大化它的泛化能力，即最大化受试者工作特征曲线（Receiver Operating characteristic Curve， ROC）下的面积和F-度量，其中运用了高斯混合模型和正交前向子空间选择方法。支持向量机在类之间数据不平衡的情况下表现不佳，特别是在目標类的表示不足的情况下。

文献[16]通过转移决策边界和使用不相等的正则化代价两种思想，来解决在近贝叶斯支持向量机中的不平衡分类问题，方法的具体实施过程中选择每个类别中的一小部分样本代表每个类别，以实现边界的转移和不等的正则化代价。

文献[17]中通过对向正、负类样本施加不同的惩罚因子并在约束条件中增加参数来处理不平衡样本的分类问题。本文则通过对每个类标签的数据进行分别处理，尽量在每个类中选择相近个数的边界样本，以解决不平衡数据集所产生的误分问题。

2 数据锥及凸边界样本的定义

本文针对数据分类任务，提出了一种基于凸边界的样本选择方法。在本文方法的研究初期，需要对此方法思想进行保护，因此申请了专利[18]，并在本文中对方法的理论环节进行了深入，在方法的具体实施步骤中进行了改进和细化。方法的理论如下：

首先，将给定的数据集 D 分为训练集 D 1和测试集 D 2：

D = D 1∪ D 2

（1）

在训练集 D 1中，本文方法将在每个类标签上选择边界样本，

D 1= D 11∪ D 12∪…∪ D 1i; i=1，2，…，M

（2）

其中，M为类标签的个数，即本文方法在每个 D 1i中选择边界样本。

在先前的工作[18]中，未对凸集合的思想如何应用在方法中进行说明，也未对选择边界样本的选择空间进行定义，仅简单地在坐标系的每个象限中进行边界样本的选择。在本文的研究工作中则提出了数据锥的概念，边界样本在每个数据锥中进行选择。数据锥是基于凸锥的思想而提出的定义，凸锥属于锥形，也是一种特殊的凸集，具有着凸集合的性质。因此，可以应用关于凸集的最经典的凸优化问题的解决思路。即本文基于凸集合的边界样本选择方法，实际上是解决一个凸优化问题，即可行域是一个凸集，目标是一个凸函数。本文方法所要实现的就是在数据锥中选择最少的样本作为训练集，加快建模速度、减小内存开销，而保持分类准确率不变，甚至提升，从而提升数据分类的性能。

本文方法在每个 D 1i子集中根据训练集 D 1的维度构建多个数据锥，在每个数据锥中选择边界样本。数据锥的定义如下：

C ={ x ∈ R n |x ∈ C ，λ>0，λ x ∈ C }

（3）

式（3）表示：对于数据锥中的任一点 x ，在通过放大系数λ放大后，仍属于这个数据锥中的一个元素。之后，本文方法要在所构造的每个数据锥中基于凸边界的概念选择样本。为更好地理解凸边界的概念，先给出边界的定义：

B （ I ）= { x ∈ I  | ε>0， x ′， x ″∈N（ x ，ε）， x ′∈ I ， x ″∈ I  }

（4）

N （ x ，ε）={ y ∈ R n | ‖ y - x ‖<ε}

（5）

I  = R n/ I

（6）

式（4）～（6）表示：对于边界中的一点 x ，对任一ε，以 x 为圆心，ε为半径作一邻域 N ， N 中存在两点 x ′和 x ″，其中， x ′属于边界 I 中， x ″是边界 I 外的一点。由这样的 x 构成的集合即为边界集 B （ I ）。

已有边界的定义以后，即可给出凸边界的定义：

CB （ I ）= { x ， y ∈ B （ I ） | λ∈[0，1]，λ x +（1-λ） y ∈ CB （ I ）}

（7）

式（7）表明：在边界集 B （ I ）中的两点的连线属于凸边界 CB （ I ）。最终，本文方法将在凸边界 CB （ I ）中选择代表性样本。

最后，本文方法的目的是最小化训练集的样本个数，但分类准确率与原始训练集 D 1相近或小幅下降，从而提升分类器性能。即：

| p（Α（ CB （ I ）， D 2））-p（Α（ D 1， D 2）） | <ε

（8）

其中：Α是一个学习算法，p（Α（ D 1， D 2））表示以 D 2为测试集， D 1为训练集，在算法Α上得到的分类精度;ε为允许的最大的分类准确率差异，超过这个设定的值，则可认为样本选择方法无效。本文设定ε的值为10个百分点。

3 算法伪代码

本文边界样本选择方法的具体实现分为两部分：首先，对用户给出的数据集进行预处理，根据类标签进行子集的划分;然后，在每个子集中建立多个数据锥，并在每个数据锥中选择边界样本。

算法中的符号含义如下： T 表示原始训练集， T 1表示删除含缺失值样本后的数据集， T 2表示删除含异常值样本后的数据集， T 3表示归一化后的数据集， T 3k表示分割后的子集， T 4k表示坐标变换后的结果， BS （Boundary Samples）表示原始训练集的边界样本， BS i表示第i个子集的边界样本。

3.1 数据集的预分割

算法1：数据集的预分割。

程序前

输入原始训练集 T

删除包含缺失值的样本后，得到 T 1

if   T 1中存在数值全部相同的特征 then

删除此特征

end if

判断特征之间的相关性，删除冗余特征

提取 T 1中的类别标识 C ，及标识个数C_N

fo r i=1：C_N do

从 T 1中提取属于第i个类别的所有样本，得到 S i

在 S i的每个特征中，使用箱型图检测异常值，并删除包含這些异常值的样本

end for

如果存在某特征上的数值全部相同，恢复对此特征上去除的异常样本

得到删除异常样本后的数据集 T 2

对 T 2进行归一化，得到 T 3

fo r i=1：C_N do

在 T 3中提取第i个类标识的样本子集 T 3i

end for

输出多个子集 T 3k

程序后

在数据集的预处理过程中，对先前工作[18]进行了细化及改进。改进如下：在进行异常样本检测前增加了对于无用特征及冗余特征的判别和删除操作。当存在无用特征或冗余特征时，会影响数据锥的构建及增加边界样本的个数，且会增加方法的执行时间。在异常样本删除后，增加了检测特征值是否相同的操作，其目的是保证异常样本删除后特征不会变成对于数据分类任务的无用属性，且不会对后续的归一化操作造成影响。

3.2 构建数据锥及提取边界样本

算法2：构建数据锥并提取边界样本。

程序前

输入多个预处理后的子集 T 3k

fo r i=1：C_N do

选取第i个子集 T 3i

if  子集 T 3i中只包含一个样本 then

选择此样本作为一个边界样本

el se

计算 T 3i的中心点 center i

将 T 3i的原始坐标系变换成以 center i为原点的新坐标系，得到新的子集 T 4i

对 T 4i的中的每个样本添加一个索引，以标识它所属的数据锥

统计现已存在的数据锥，得到 Cone ，并计算数据锥的个数Cone_N

fo r j=1：Cone_N do

在 T 4i中，根据索引提取属于第j个数据锥的所有样本 CS

if   CS 只包含一条样本 then

从原始数据集 T 选择这条样本，作为 b j

el se

计算 CS 中每个样本到坐标系原点的距离，得到 distance

end if

end for

得到第i个子集的边界样本 BS i：

BS i= b 1∪ b 2∪…∪ b Cone_N

end if

end for

得到原始训练集 T 的边界样本集 BS ：

BS = BS 1∪ BS 2∪…∪ BS C_N

程序后

在边界样本的选择过程中，对先前工作[18]的改进如下： 1）针对每个子集中包含的不同样本数作相应处理，以加快方法的执行速度;

2）明确了凸集合在本文方法中的应用，通过对每个子集构造多个数据锥后，应用凸集合的性质，而不是简单地将变换后的坐标系空间作为一个凸集合，对边界样本的选择更加明确，只选择每个数据锥中的边界样本，即对分类任务起决定作用的样本，能更好地维持原始训练集的分类准确率。最后，不使用哈希表记录每个样本所属象限，因为当特征数多时，象限数会急剧增加，相应的哈希表会增大，而哈希表非常大时将会消耗较大的内存。在本文方法中通过对样本的简单标识，可区分属于哪个数据锥中即可，从而减少内存的开销;而且通过遍历数据锥而不是每个象限能加快方法的执行速度。

4 实验结果及分析

4.1 数据集

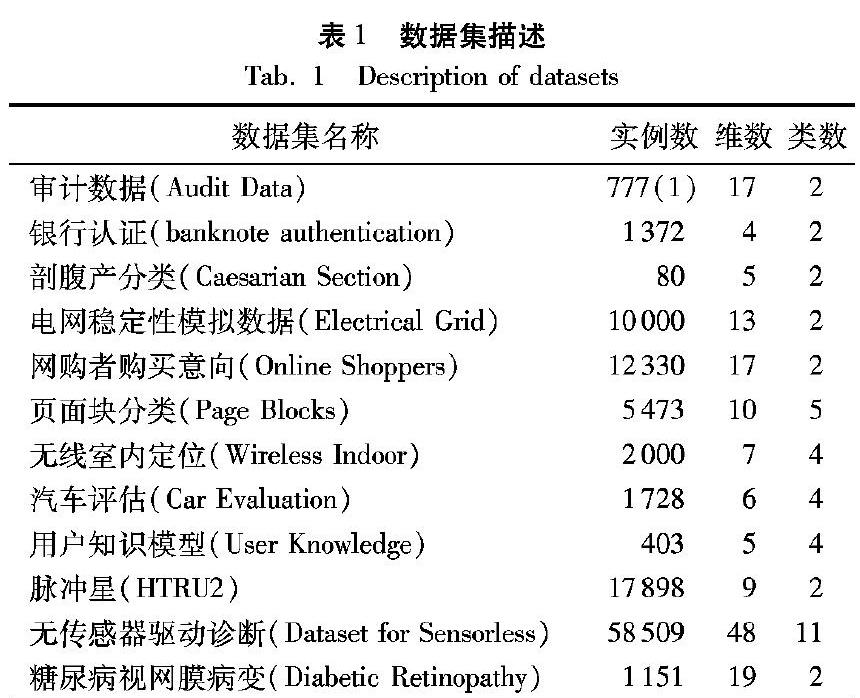
在实验评估部分，本文选择了12个主要用于分类任务的UCI数据集（可在http：//archive.ics.uci.edu/ml/获取）来测试基于凸边界的样本选择方法。由于数据集的详细属性较多，这里只展示对本文起关键性作用的几个描述（其中数据集英文名称过长的仅保留前2～3个单词），具体如表1所示。

通过表1“实例数”数值可知，实验既选取了较少的仅有80条样本的剖腹产分类数据集，也选择包含58509条样本的无传感器驱动诊断数据集，其中“（）”中的值表示包含的缺失值的个数。“维数”表示实际输入到算法中的特征的个数，本实验选择了从较少的4个特征到较多的48个特征的数据集。由实例数与维数这两列数值可知，本实验数据集的选取较为全面。“类数”是方法中子集分割的关键因素，其中包括6个二分类数据集和6个多分类数据集，最多的一个无传感器驱动诊断数据集包含11个类别。与先前工作[18]的实验环节相比较，本文重新选择了多个近五年的新数据集，且增大了数据集的实例数。

4.2 实验设置

由于基于凸边界的样本选择方法主要针对分类任务的数据集的预处理，因此本文在Python的scikit-learn包中选取了6个常用的分类器来验证该方法的可行性和有效性。这6个分类器分别是：高斯朴素贝叶斯（Gaussian Naive Bayes， GNB）、決策树（Classification And Regression Tree， CART）、线性判别分析（Linear Discriminant Analysis， LDA）、提升算法（Adaptive Boosting， AdaBoost）、随机森林（Random Forest， RF）和逻辑回归（Logistic Regression， LR）。与先前工作[18]的实验环节相比，本文选择了当下流行的python中的sklearn包中的六种经典的分类器，增加了分类器选择的多样性，从而验证本文方法是否具有普适性。对于分类任务的评估，通常选择分类准确率作为其主要性能指标。因此，本文采用了分类准确率作为实验结果的展示。

实验中使用的12个UCI数据集，在各类别中按照2∶ 1的比例将样本划分为两部分，以保证用于分类任务的数据集在划分前后的类别占比一致，保持了原数据集中的类别分布结构。即训练集 D 1占样本总数的2/3，测试集 D 2包含剩余的样本。之后，将训练集 D 1输入到本文提出的样本选择方法中得到边界样本集 BS 。将训练集 D 1和边界样本集 BS 分别作为6个分类器中训练集的输入，测试集的输入为 D 2，对比原训练集与边界样本集的分类准确率，从而验证本文方法的可行性。为了进一步验证本文方法的性能，通过样本量之比和分类准确率之比，给出了样本选择的效率分析公式，将在4.4节中详细介绍此内容。

4.3 实验结果

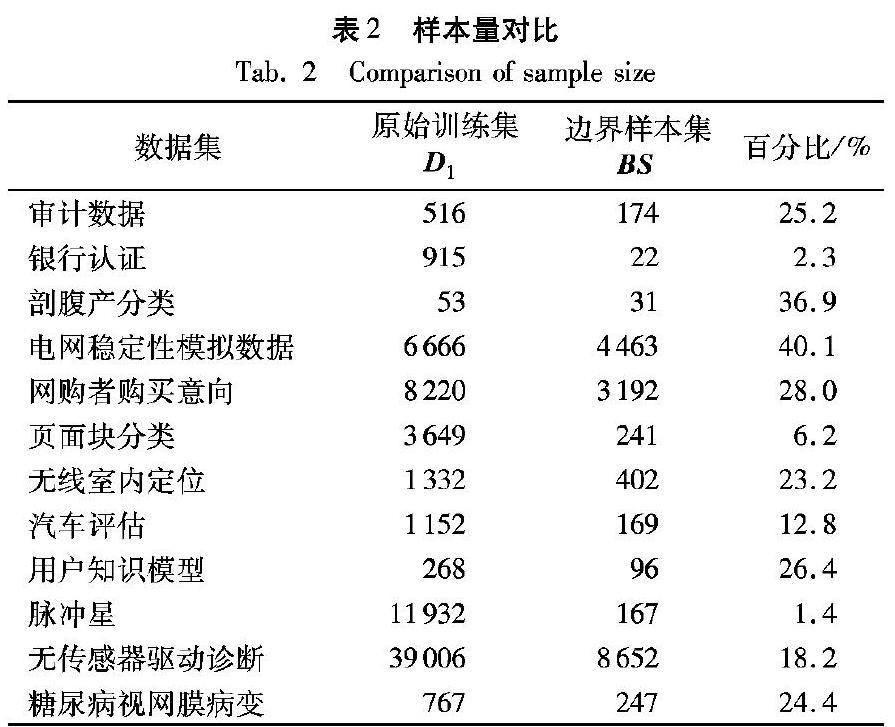
原始训练集 D 1和边界样本集 BS 之间样本量的比较如表2所示。 为了更清楚地观察样本量的差异，表2的最后一列中给出了样本量的百分比。对表2中的“百分比”表示 BS 的样本量与 BS 和 D 1样本量之和的比值。例如，糖尿病数据集，原始训练集和边界样本集共1014条样本，其中 D 1约占1014条的75.6%，共767条， BS 包含247条样本，约占24.4%。

依据表2的结果展示，与原始训练集 D 1的样本量相比，边界样本集 BS 的样本量显著减少。银行认证、页面块分类、汽车评估和脉冲星数据集的样本减少量相当大，其中脉冲星数据集的 BS 的样本量较 D 1减少了约98.6%，初步显示了本文提出的样本选择方法可有效减少用于训练的样本量。而剖腹产和电网稳定性数据集的减少量相对较小，各减少了37.7%和33%。这是因为边界样本的选择主要取决于处理 训练集 D 1时所构造的数据锥，数据锥的数量越多，选择到的边界样本就越多，而数据锥的数量主要取决于数据集的维数、类数和数据自身的分布结构。

其次，为了验证本文方法在减少样本量的同时仍可保持原始训练集的分类性能，分别在6个分类器上进行了12个UCI数据集的分类实验，比较了原始训练集 D 1和边界样本集 BS 分别作为训练集时的分类准确率，结果见表3。结果中加粗字体部分表示用边界样本集 BS 作为训练集的分类准确率高于或等于原始训练集。可通过数据的直观对比分析本文方法的可行性和有效性。

4.3.1 高斯朴素贝叶斯

高斯朴素贝叶斯（GNB）是一种用于处理连续的特征变量的朴素贝叶斯分类器。朴素贝叶斯分类器是基于贝叶斯定理的一种非常简单的概率分类器，具有稳定的分类效率，且分布独立假设成立的情况下效果最佳，因此，本文选择它作为实验的分类器之一。

通过比较表3中GNB分类准确率结果可以看出，用边界样本集 BS 作为训练集在GNB分类器上进行分类预测，其分类准确率结果与原始训练集 D 1的准确率相差不大。其中剖腹产、网购者意向、无传感器诊断、糖尿病这4个数据集在使用边界样本集 BS 后的分类准确率得到了提高。边界样本集 BS 较原始训练集 D 1的分类准确率下降的最大程度仅为8.9个百分点，为汽车评估，但其边界样本数与 D 1的样本数相比减少了85.3%。由于训练样本大量减少而出现的分类准确率小幅下降的情况，在预期的可接受范围内。因为减少构建分类模型的样本量，可以大大减少建模的时间和内存消耗;并且对于绝大多数数据集而言，利用边界样本 BS 作为GNB分类器的训练集，得到的结果都很好，表明本文提出的方法具有一定的可行性。

4.3.2 决策树

CART决策树是一种典型的二叉决策树，既可用作回归也可用于分类，当作为分类树时采用基尼指数来选择最优的切分特征，并且分类规则易于理解。

在CART决策树的结果中，剖腹产数据集在使用边界样本集 BS 后的分类准确率有所提高，提升了3.9个百分点;而审计数据和电网稳定性这两个数据集的分类准确率在训练样本减少后仍保持不变。然而有2个数据集的结果较不理想，其中页面块分类数据集在使用边界样本后的分类准确率较原始训练集 D 1下降了9.8个百分点，脉冲星数据集的分类准确率则下降了9.1个百分点，但分析样本对比量后可知，边界样本集 BS 较原始训练集 D 1的样本数大量减少，导致了分类准确率下降的情况。但多数边界样本集 BS 的分类准确率下降约在5个百分点以内。总体结果表明，利用边界样本训练分类器达到了预期的目的。

4.3.3 线性判别分析

线性判别分析（LDA）也称Fisher线性判别，其基本思想是将高维空间中的样本投影到最佳鉴别矢量空间，以达到抽取分类信息的效果，保证在该空间中有最佳可分离性。

据表3中的结果显示，有2个数据集的分类准确率的结果在使用边界样本集 BS 作为训练集后保持不变，分别是无线室内定位和用户知识模型，而在此分类器上没有准确率得到提升的数据集。除糖尿病数据集较原始训练集 D 1的分类准确率下降了7.5个百分点外，其他数据集准确率的下降幅度大约都在4个百分点以内。在表3的LDA结果比对中，大部分数据集的分类准确率都相差不大，并且用于训练的样本数量的大幅减少，可以说明本文的样本抽取方法对数据集的预处理工作有所成效。

4.3.4 提升算法（AdaBoost）

提升算法（Adaboost）是一种迭代算法，它运用集成的思想，将由同一训练集训练的多个不同的弱分类器组合成一個强分类器。在本实验中，弱分类器使用了默认的CART决策树，AdaBoost的算法选择了SAMME，它将对样本集的分类效果作为弱分类器的权重。

根据AdaBoost的分类准确率结果可知，剖腹产数据集的分类准确率提升了11.5个百分点，其原因是在选择边界样本的过程中剔除了噪声样本。审计数据和电网稳定性数据集的准确率较原始训练集 D 1未发生改变。其中，页面块分类数据集在使用边界样本后结果较差，下降了9.6个百分点。其他的数据集在使用边界样本训练得到的分类准确率与使用原始训练集 D 1的准确率相差不大。但结合训练样本数减少的综合分析，这些结果依旧可以表明用边界样本集 BS 作为训练集的方法是可行的。

4.3.5 随机森林

随机森林是一种集成算法，它包含多个决策树，并且其输出类别由个别树输出类别的众数决定，即通过投票的方式决定最终的分类结果。其中每棵树在构建的过程中随机选取特征，保证随机森林的多样性和随机性。

在表3中RF的结果显示，剖腹产和电网稳定性数据庥的分类准确率得到了改善，其中电网稳定数据集在适用边界样本进行训练后的准确率达到了100%，即选择得到的边界样本集 BS 中不含噪声数据。审计数据集的分类准确率在使用边界样本进行训练后保持了分类准确率不变。

用户知识模型（准确率结果加下划线显示）数据集的准确率下降了13.3个百分点，超过了本文设定的10个百分点的限制。根据表2中的样本量对比可知，边界样本数较原始训练集减少了64.2%，选择到的96条边界样本可能无法满足使用随机森林分类器时所需的全部信息，因此出现了大幅下降的情况。随机森林分类器对于小数据或低维数据来说，不能产生很好的分类效果，因此由于边界样本数过少导致了此情况的发生。但根据其他数据集的结果仍可认为本文提出的样本选择方法是可行的。

4.3.6 逻辑回归

逻辑回归模型是一个非线性模型，使用sigmoid函数，又称逻辑回归函数，但它本质上又是一个线性回归模型，且常用于二分类问题，可扩展至多分类。

在表3逻辑回归分类器的结果中，网购者意向、无线室内定位、汽车评估、无线传感器诊断这4个数据集的分类准确率有所提升。与随机森林分类器中出现的情况一样，用户知识模型数据集使用边界样本集 BS 作为训练集后的分类准确率下降了21.5个百分点，远远超出了本文设定的10个百分点的要求。结合LR分类器的特性与训练样本数的减少情况分析，LR要求训练集中的样本线性可分，由于训练样本较少，且本文提出的样本选择方法选出的样本都是具有歧义性的、最模糊的、易分错的样本，因此无法很好地满足LR分类器的要求，导致了分类准确率大幅下降的情况出现。因此，虽有此情况的出现，由其他数据集的结果中可知，本文方法仍是有效的。

综合五个分类器的实验结果和样本量的对比，可得出一些结论：

在这12个数据集中，绝大部分数据集经过本文方法选择得到的边界样本集 BS 的样本量较原始训练集 D 1有着明显的减少。这是由于边界样本集 BS 的样本数量与数据集中类数和维数（即数据集的固有特征）有关。类标识和属性的个数越多，数据分布得越均匀，经本文方法选择到的边界样本的数量就越多。

其次，从表3的实验结果中可以看出，使用边界样本集 BS 对不同的分类器进行训练后得到的模型的分类准确率大致相同。因此，可知使用边界样本进行训练的结果并不受分类器种类不同的影响，即基于凸边界的样本选择方法适用于多种分类模型。表3的具体结果表明，以边界样本 BS 为训练集，可以提高6个分类器中部分数据集的分类准确率。剖腹产数据集在4个分类器上的分类准确率都有所提升，说明本文方法去除了影响这些分类器分类性能的噪声数据。而由于用于训练的样本数量的减少，与原始训练集 D 1的结果相比，单个数据集的准确率降低几乎都在10个百分点以内，并且大多数数据集的准确率降低都小于5个百分点，跟原始训练集 D 1的结果相差不大。因训练样本数量大幅度减少，准确率的小幅下降是不可避免的。但其中页面块分类和用户知识模型在使用边界样本集后分类效果较差，页面块边界样本量较原始训练集 D 1减少了93.4%，用户知识模型减少了64.2%，会出现边界样本因样本数过少而导致信息包含不全的情况，但也因此换来了训练时间的大量减少。而大部分数据集在6个分类器上的表现很出色，因此，本文的实验结果是可以接受的，并达到了本文方法的预期效果，说明提出用边界样本集 BS 作为训练集是可行的。并且，利用边界样本可以加快分类器的建模速度，降低内存开销，在分类准确率降低很小的情况下，能从整体上提高分类器的性能。

4.4 效率分析

4.3节中，在使用边界样本集 BS 之后，每个数据集用于训练的样本量大量减少，从而加快了机器学习的速度。然而，由于某些数据集的准确率降低，需要一个标准来衡量本文提出的方法是否对数据分类任务有效。因此，本文提出了一个新的概念，即清洗效率，来判断该方法的有效性。

4.4.1 清洗效率定义

样本量的减少率：

P1=N0/N1

（9）

其中：N0是原始训练集 D 1的样本个数，N1是经本文方法选择得到的边界样本集 BS 的样本个数。

准确率的减少率：

P2=T0/T1

（10）

其中：T0是由原始训练集 D 1得到的分类准确率，T1是由边界样本集 BS 得到的分类准确率

因此，清洗效率被定义为：

P=P1/P2

（11）

其中：P1代表提取的边界样本数量相对于原始训练样本数量的缩减程度，P1的值越大，表明在此度量上使用本文方法选择的边界样本集 BS 作为训练集时的效果越好;P2代表使用边界样本集 BS 的分类准确率较原始训练集 D 1的准确率差的程度，P2的值越小，表明本文方法的效果越好。因此，综合这两个指标的比值可知，P的值越大，使用邊界样本集 BS 进行数据分类任务的效率就越高。

4.4.2 清洗效率结果

根据清洗效率公式的定义，将6个分类器上12个数据集的效率分析结果汇总在表4中（表4中将AdaBoost缩写为Ada）。

根据清洗效率公式的定义：当P>1时，即可认为该方法提高了数据分类的效率，数值越大，提升效率越高，即此方法在这个数据集上的表现越好;如果P<1，说明该方法降低了数据分类的效率，则可认为无法用此方法选择到的边界样本集 BS 作为训练集进行数据分类任务。

从表4可以看出，清洗效率的所有值都大于1，说明本文方法是有效的。银行认证、页面块分类和脉冲星这三个数据集的清洗效率结果都大于10（名称及清洗效率结果加粗显示），其中脉冲星的效率高达68以上，是效果最显著的一个数据集。结合表2进行分析，这3个数据集的边界样本数较原始训练集 D 1的样本数大量减少，因此在效率公式中P1的值较大，且使用边界样本集 BS 的分类准确率的下降程度较小，从而清洗效率P值更大。并且脉冲星数据集的原始训练集 D 1包含的样本数也较大，可以说明原始数据集样本量越大，本文方法的效果越好，数据分类效率越高。这一结论对本文方法在大规模数据集中的应用具有积极的肯定意义。

5 结语

本文提出了一种基于凸边界的样本抽取方法，针对数据分类任务，从样本约简的角度来提升机器学习的性能;在实验环节中，通过样本量对比、分类准确率对比和效率分析，验证了本文方法的可行性及有效性，并得出了本文方法适用于大多数分类器的结论。但实验中“用户知识模型数据集”的分类准确率结果因样本量的大幅减少及分类器自身的建模方式，降低了20个百分点左右。在后续研究中，我们将针对此类问题进行探究，探寻扩展到其他机器学习任务中的样本选择方法，从而提出一种通用且高效的样本预处理方法。

参考文献

[1] 刘艳，钟萍，陈静，等.用于处理不平衡样本的改进近似支持向量机新算法[J].计算机应用，2014，34（6）：1618-1621. （LIU Y， ZHONG P， CHEN J， et al. Modified proximal support vector machine algorithm for dealing with unbalanced samples [J]. Journal of Computer Applications， 2014， 34（6）： 1618-1621.）

[2] de CARVALHO M G， LAENDER A H F， GONCALVES M A， et al. A genetic programming approach to record deduplication [J]. IEEE Transactions on Knowledge and Data Engineering， 2012， 24（3）： 399-412.

[3] dal BIANCO G， GALANTE R， HEUSER C A， et al. Tuning large scale deduplication with reduced effort [C]// Proceedings of the 25th International Conference on Scientific and Statistical Database Management. New York： ACM， 2013： No.18.

[4] dal BIANCO G， GALANTE R， GONALVES M A， et al. A practical and effective sampling selection strategy for large scale deduplication [J]. IEEE Transactions on Knowledge and Data Engineering， 2015， 27（9）： 2305-2319.

[5] WANG X， DONG L， YAN J. Maximum ambiguity-based sample selection in fuzzy decision tree induction [J]. IEEE Transactions on Knowledge and Data Engineering， 2012， 24（8）： 1491-1505.

[6] OUGIAROGLOU S， DIAMANTARAS K I， EVANGELIDIS G. Exploring the effect of data reduction on neural network and support vector machine classification [J]. Neurocomputing， 2018， 280： 101-110.

[7] SHEN X， MU L， LI Z， et al. Large-scale support vector machine classification with redundant data reduction [J]. Neurocomputing， 2016， 172：189-197.

[8] 胡小生，钟勇.基于边界样本选择的支持向量机加速算法[J].计算机工程与应用， 2017， 53（3）： 169-173. （HU X S， ZHONG Y. SVM accelerated training algorithm based on border sample selection [J]. Computer Engineering and Applications， 2017， 53（3）： 169-173.）

[9] DESSì N， PES B. Similarity of feature selection methods： An empirical study across data intensive classification tasks [J]. Expert Systems with Applications， 2015， 42（10）： 4632-4642.

[10] ZHANG Y， YANG C， YANG A， et al. Feature selection for classification with class-separability strategy and data envelopment analysis [J]. Neurocomputing， 2015， 166： 172-184.

[11]  BOLN-CANEDO V， SNCHEZ-MAROO N， ALONSO-BETANZOS A. Data classification using an ensemble of filters [J]. Neurocomputing， 2014， 135： 13-20.

[12]  RIVERA W A， XANTHOPOULOS P. A priori synthetic over-sampling methods for increasing classification sensitivity in imbalanced data sets [J]. Expert Systems with Applications， 2016， 66： 124-135.

[13] MENARDI G， TORELLI N. Training and assessing classification rules with imbalanced data[J]. Data Mining and Knowledge Discovery， 2014， 28（1）： 92-122.

[14] LóPEZ V， FERNáNDEZ A， HERRERA F. On the importance of the validation technique for classification with imbalanced datasets： addressing covariate shift when data is skewed [J]. Information Sciences， 2014， 257（2）： 1-13.

[15] GAO M， HONG X， HARRIS C J. Construction of neurofuzzy models for imbalanced data classification [J]. IEEE Transactions on Fuzzy Systems， 2014， 22（6）： 1472-1488.

[16] DATTA S， DAS S. Near-Bayesian support vector machines for imbalanced data classification with equal or unequal misclassification costs [J]. Neural Networks， 2015， 70： 39-52.

[17] 劉艳，钟萍，陈静，等.用于处理不平衡样本的改进近似支持向量机新算法[J].计算机应用，2014，34（6）：1618-1621. （LIU Y， ZHONG P， CHEN J， et al. Modified proximal support vector machine algorithm for dealing with unbalanced samples [J]. Journal of Computer Applications， 2014， 34（6）： 1618-1621.）

[18]  袁玉波，顾依依，谈询滔，等.一种基于凸边界的学习样本抽取方法： CN201711314980.2[P]. 2018-05-18. （YUAN Y B， GU Y Y， TAN X T， et al. A learning sample extraction method based on convex boundary： CN201711314980.2 [P]. 2018-05-18.）