小学数学例题的合理改编
2019-10-23于飞
于飞
当前,例题教学大多存在教教材、拿来主义等问题。虽然教材凝聚着众多专家的智慧,是文本解读的第一文本,但它也不是唯一的、不可改变的。随着时代和学生的发展,教师要善于根据教材例题特点和学情,创造性地改编教材,以使学生更好地理解问题,发展他们的数学关键能力。
以人教版《数学》五年级上册“用字母表示数”一课为例,这是学生由算术思维迈向代数思维的起点,是后续学习代数知识的基础。教材在编排时直接从用含有字母的式子表示数量关系开始,采用两个材料:一是“爸爸比女儿大30岁”,引出“a+30”,二是“月球上人能举起的物体质量是地球上的6倍”,引出“6x”。笔者在一次教学研讨活动中,对例题做了改编,借助五个微信红包,设置三处思辨,成功实施了教学。
一、创设学习情境——由被动走向主动
合适的情境能激发学生的学习情感。创设符合学生年龄和生活特点的素材,有助于调动学生的情绪、激发学习兴趣,有助于学生更直观和便捷地理解教材。
“用字母表示数”作为发展代数思维的起始课,更应该优选合适的情境素材。教材例1和例2呈现的情境远离生活,缺乏兴趣,学生探究欲望弱,被动学习新知识。因此,笔者对其进行改编。
【教学片段1】
师:同学们有抢过微信红包吗?谁能说说你的抢红包经历?
(一下子点燃了课堂的氛围,学生踊跃举手。)
学生说经历......
师:逢年过节收到红包是一件很开心的事,微信让红包变得方便而有趣。现在有两个红包(课件出示两个微信红包:第一个红包已经打开,显示8.80元,第二个红包未点开。
微信红包是学生非常感兴趣的新鲜事物,它贴近实际生活,富有乐趣,大多数学生都有抢红包的快乐经历。因此,本课先用微信红包作为课前谈话的话题,充分调动学生的学习兴趣和积极性,激起探究欲望,再顺势出示两个不同的红包,开始新课的学习,使学生从被动学习,转向主动学习。
二、串联学习素材——由孤立走向联系
新授环节切换情境是把双刃剑,它需要学生有一个再认识、再进入的过程,频繁的切换有碍于学生对新知识的理解,使学生把注意力过多地放在情境的解读上。若能用同一情境串联起多个知识点,把原本孤立的、互不相干的多个情境联结起来,就会给学生的学习带来便利。
“用字母表示数”这一课的教学目标较多,笔者将这些目标,用同一情境——微信红包,串联呈现,收到了很好的效果。本课在新授环节课件一共出示以下5个不同的红包:
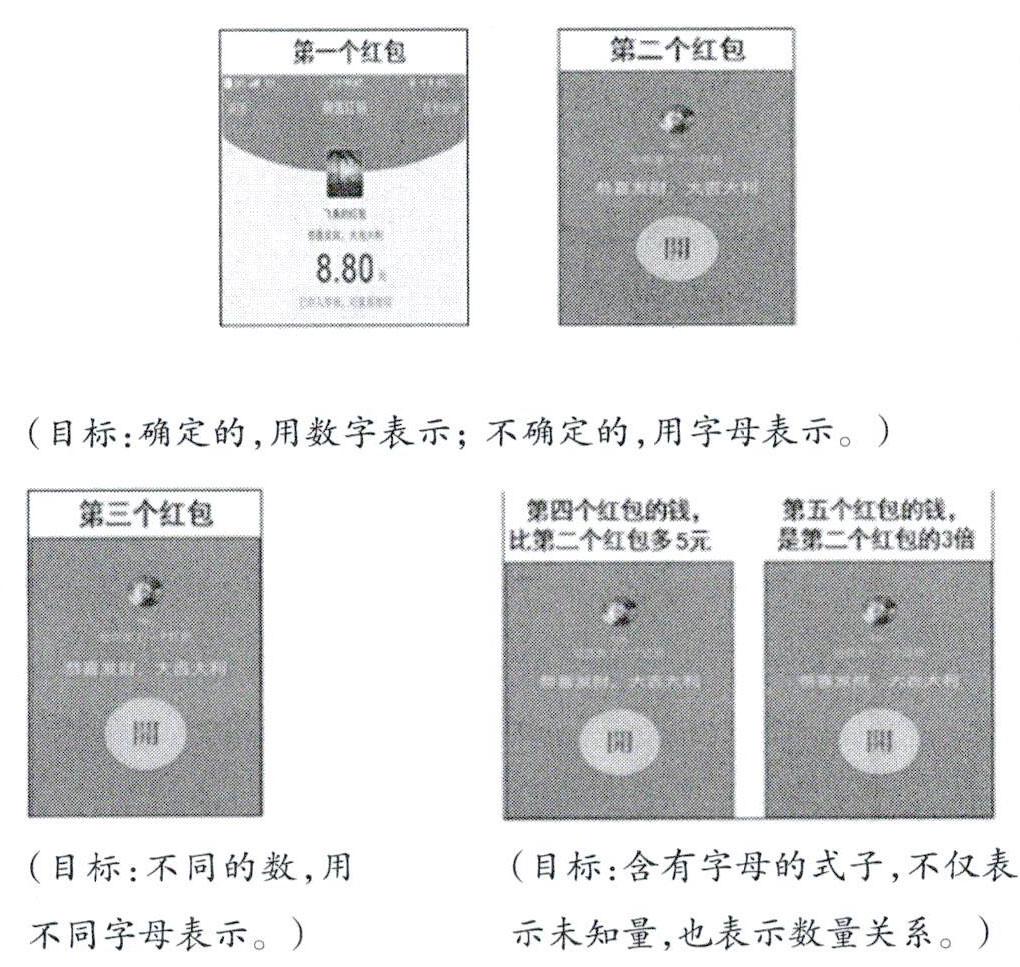
五个红包,把原本教材中“女儿和爸爸年龄、月球上的体重”两个完全不同、孤立的情境,改编成一个情境,使所有教学目标的达成,都在红包情境下展开。五个红包,因为有不同的信息,指向不同的目标,所以在实际教学中不会给学生造成视觉疲劳,反而会不断地给学生兴趣上的刺激,使他们集中注意力突破本课重难点。
三、激活教学重难点——由知识走向思维
例题改编不只是为了呈现富有乐趣的素材,激发学生探究欲,其最终目的一定是为了学生更好地突破重难点。当我们苦思冥想如何创设情境时,首先要思考:改编是否有助于突破教学重难点。
針对“用字母表示数”的例题改编,五个微信红包的素材,吸引了学生的兴趣,但最终是为了帮助学生更好地理解和掌握用字母表示一个数或数量关系,体会用字母表示数的概括性和简便性,感悟符号化和代数思想。因此,在教学中设置三处思辨,让学生知其所以然。
1.第一次思辨——8.80与a的不同
通过前两个红包的学习,学生经历了从确定的数(8.80)到不确定的数(a)的过程,体会了用字母表示数的简便性及其意义,再带领学生思辨:两个红包分别用8.80和a表示,有什么不同?问题指向数字和字母的区别。
【教学片断2】
师:刚刚用8.80和a表示红包的钱数,有什么不同?
生1:8.80元这个红包是已知的,告诉我们的;a 元这个红包还没有打开,不知道它的钱数,是未知的。
生2: 8.80元是确定告诉我们的; a 元是不确定的,还没打开。
师:板书:已知 未知。
小结:已知的用数字表示,未知用字母表示。
2.第二次思辨——第三个是a还是b?
教材没有呈现“不同的数,用不同的字母表示”这一知识点,笔者在实践中让学生充分思考:为什么可以用b、x、y......,唯独不能用a表示第三个红包的钱数?感受用字母表示数的多元性。
【教学片段3】
课件出示第三个红包,多少元呢?
呈现了:b、x、a三种典型答案。
师:这些字母都表示未知的数,都可以用来表示第三个红包吗?
生1:a不可以,因为如果是a的话,就和第二个红包相同了,两个应该是不一样的。
生2:我也觉得a不可以,因为两个红包的钱数一般是不一样的,如果都用a,那就重复了。
师:是啊,不同的数字用不同的字母表示。所以第三个用b、x是可以的,统一用b来表示第三个红包的钱数吧。
3.第三次思辨——第四个是x还是“a+5”?
用字母表示的数从一个量到一个数量关系,是本课难点。学生不习惯将“a+5”视为一个量,而认为这是一个式子,不能表示结果,所以较多学生用字母x表示。而用式子表示一个量是后续学习方程不可或缺的基础。对这个难点的突破,笔者充分借用第二、第三两个红包的基础,首先肯定学生用x是有道理的,进而再让学生回顾信息,找出最合适的答案。
【教学片段4】
课件呈现第四个红包:比第二个红包多5元。
师:第四个红包钱数怎么表示?
学生的典型答案:x和“a+5”,x居多。
师:怎么想的?
生1:虽然第四个比第二个多5元,但还是不知道第四个到底是多少,所以用x表示。
师:未知的用字母x表示,有不同的想法吗?
生2:我认为是“a+5”,因为它说“比第二个多5元”,如果用x表示就看不出“多5元”,用“a+5”就可以表示出这个关系。
师:“a+5”不仅表示一个数,也表示与第二个红包之间的数量关系。所以第四个红包用“a+5”表示更合适。
五个红包环环相扣,设置三处思辨,突出重点,突破难点:理解用字母表述数和数量关系,体会用字母表示数的简洁性。特别是在理解用字母表示数量关系上,学生能够借用红包情境,通过思考讨论,理解其意义。
四、发现和提出问题——由理解走向运用
改编例题是为了帮助学生理解和突破重难点,最终发展学生数学核心素养。结合改编的例题和课堂生成的学习材料,引领学生发现问题和提出问题,既能巩固与提升,又能产生新的问题,引发学生深入思考。
用含有字母的式子表示数量关系,通过第四、第五个红包的学习,已经对其有所理解,但还没有达到运用的程度。因此,可以充分利用五个红包和生成的结果,引领学生发现和提出问题,加以巩固和提升。
【教学片段5】
师:根据五个红包的信息,你能提出哪些数学问题?
生1:第二个和第三个共几元?
生2:第四个是第二个的几倍?
生3:第五个比第四个多几元?
生4:五个红包一共有多少元?
......
让学生解答问题并解释。
好问题源于学生对用字母表示数的理解。生成的众多问题,均指向本课难点:用含有字母的式子表示数量关系。发现和提出问题,不仅是对重难点的深入理解,更是考查学生能否在理解的基础上形成灵活运用能力。
当例题素材不适合学生的学习起点和经验时,作为教师应该创设贴合学生学习兴趣的情境,新情境既能助力教学重难点的展开,也有一定開放度,培养学生问题意识,最终发展学生数学核心素养。例题改编过程中应注意两点:一是教师要具备一定的例题改编能力。例题是教学的重要载体,但在新的时代,由于教材审核的周期性,有些例题不一定适应现在学生的需求,因此不假思索全部照搬所有例题,是不可取的。教师对教材既要有敬畏之心,又要有创新的勇气。二是作为教师,首先要想清楚:为什么要改编例题?如果仅仅是为了“花哨”,只会适得其反。刻意为之,是对教材的不尊重。 例题的改编,一定是在教师研读教材,抓住学生认知起点和生活经验,审视和比对新例题与教材例题的优缺点,当有教学需要时,才选择改编,是因教学内容和教学目标的需要,而不是为了改编而改编。
[责任编辑:陈国庆]
