花键冷挤压成形过程凹模入口半角优化数值模拟

葛 德,王培安,郭欢欢

(1．无锡商业职业技术学院机电技术学院，江苏无锡214153;2．商丘工学院机械工程学院，河南商丘476000;3．兰考职业技术学院机械与数控学院，河南兰考 475300)

冷挤压技术是一种优质、高效、低成本的成形工艺[1-6]，许多学者利用冷挤压技术对花键成形过程进行了研究，如2015年，长春理工大学的葛德等[7]利用Archard磨损模型，研究了花键成形过程中不同模具初始硬度对模具磨损的影响规律，并获得了两者的关系曲线，有效地对模具磨损量进行了预测；2016年，重庆理工大学的薛倩倩[8]基于数值模拟对输入轴花键成形过程进行分析，获得了影响花键成形极限的主要因素；2017年，重庆长融机械有限责任公司何孟林等[9]利用DEFORM软件对花键成形过程进行模拟分析，其模拟结果可靠性高，可为实际生产作理论指导，大大降低了试模成本；2018年，长春理工大学的吴淑芳等[10]对梭心零件制定了两种冷挤压成形方案，并利用数值模拟和正交试验分析两种方案的合理性，最终获得了较优的工艺方案，为梭心零件的实际生产提供理论依据。目前，花键轴冷挤压成形过程研究主要采用的软件是DEFORM，它可以获得成形载荷以及模具磨损量等信息，对于制定正确的工艺方案有一定的指导意义。本文以花键挤压成形过程为研究对象，利用DEFORM-3D软件对花键的冷挤压成形过程进行模拟，重点分析了凹模入口半角对花键成形质量的影响。

1 花键冷挤压成形工艺

1.1 研究对象的确定

本文研究的花键二维零件图如图1所示，其具体参数如下：键数N=6，大径D=10 mm，小径d=8 mm，键宽B=2 mm。该锻件花键齿面的表面粗糙度Ra=0.8 μm，其余位置表面粗糙度Ra=3.2 μm。由零件图可知，花键要求表面质量要求高、位置精度高，适合采用冷挤压进行加工。本文选用40Cr作为挤压件材料，其主要化学成分和力学性能分别如表1、表2所示。由于40Cr的硬度比较高，强度比较大，不适合直接进行冷挤压加工，需要在冷挤压前对其坯料进行退火和磷皂化等处理，使其塑性提高，抗变形力减小，从而达到冷挤压工艺需要的加工条件。

1.2 冷挤压成形工艺方案的制定

花键冷挤压成形工艺过程如下：剪切下料→软化热处理→表面和润滑处理→正挤花键→精整，其中剪切下料与正挤花键的示意图如图2所示。

1.3 毛坯形状和尺寸的确定

根据国家标准中圆钢直径选取规定[11]，初步选取毛坯圆钢的直径为φ12 mm。

图1 花键的二维零件图(单位：mm)Fig 1 2D part drawing of the spline

表140Cr钢主要化学成分
Table1Main chemical content of40Cr steel %

元素质量含量C0.37～0.44Mn0.50～0.80Si0.17～0.37Cr0.80～1.10

表240Cr钢主要力学性能(试样
毛坯长度为25mm)
Table2Main mechanical properties of40Cr steel (sample blank size is25mm)

性能指标数值 抗拉强度σb/MPa ≥980 屈服强度σs/MPa ≥785 伸长率δ/% ≥9 断面收缩率Ψ/% ≥45 布氏硬度/HBW ≤207

图2 花键冷挤压成形工艺过程示意图Fig 2 Schematic diagram of the process of spline cold extrusion forming

毛坯的外径尺寸计算如下：

d坯=d凹-(0.1～0.2)=

12-(0.1～0.2)=11.8～11.9 mm

(1)

式中：d坯为坯料直径，mm；d凹为凹模型腔内径，mm。

按照体积相等原则，利用三维软件绘制毛坯零件图，测量其体积，得毛坯体积V0=3 056 mm3。根据毛坯直径φ12 mm，毛坯高度H0计算如下：

(2)

式中：V0为坯料体积，mm3；A0为坯料横截面面积，mm2。

因此，初步确定毛坯尺寸为φ12 mm×27 mm。

1.4 挤压力的计算

挤压力的计算采用经验公式进行。经验公式简单方便，实用性强，在实际加工中运用较多。

正挤花键过程中的单位挤压力计算如下：

P=Z×n×σb=0.9×3×600=

1 620 MPa

(3)

式中：P为单位挤压力，MPa；Z为模具形状影响系数，取Z=0.9；n为挤压方式及变形程度系数，取n=3；σb为挤压前材料的强度极限，取σb=600 Mpa。

由于正挤花键过程中的单位挤压力小于模具钢所能承受的单位挤压力(2 500 MPa)[12]，故模具钢出现损坏的可能性较低。

正挤花键过程中的总挤压力计算如下：

F=c×P×A=1.3×1 620×

113.1=198.5 kN

(4)

式中：F为总挤压力，kN；P为单位挤压力，MPa；A为凸模与坯料接触面在垂直挤压力平面上的投影面积，mm2；c为安全系数，一般c≥1.3，这里取c=1.3。

正挤花键工序中压力机的大小需根据实际情况及国家标准选取。根据计算结果，建议压力机的吨位要大于20 t。

2 花键成形过程中凹模入口半角的优化

为了进行比较，需要了解优化分析之前花键凹模模具结构的重要参数。绘制花键凹模二维示意图(可以准确看出关键位置的尺寸大小)如图3所示、花键凹模三维结构渲染图(可以直观看出关键位置的空间造型) 如图4所示。

图3 花键凹模二维示意图Fig 3 2D schematic diagram of the spline die

图4 花键凹模三维结构渲染图Fig 4 3D structure rendering of the spline die

凹模入口半角是凹模模具结构的一个重要参数，其大小直接决定金属流动的均匀性﹑变形程度、成形载荷以及凹模磨损程度等，某种意义上说，它就是决定冷挤压是否可以顺利进行的关键性指标。

通常凹模入口半角过大或者过小对花键的成形质量都会造成不利的影响。在一定范围内，凹模入口半角越小，金属流动越均匀，挤出位置的横向坐标网线弯曲越小，外层与中心层金属材料的流速差距越小，变形的死区也较小，成形载荷降低；但凹模入口半角过小，金属的轴向流动位移就会变长，坯料挤压过程中与凹模型腔的接触面积将变大，摩擦阻力也会增大，为克服摩擦阻力，可能会造成总体成形载荷增大，且过小的凹模入口半角会造成过渡区长度变长，从而影响成形花键的有效长度。若凹模入口半角增大，其金属材料流动的位移量会变小，摩擦力会变小，但是变形区范围变大，挤出位置的横向坐标网线弯曲变大，金属材料外层与中心层流速的差距也变大，变形的死区也会相应增加，从而造成模具对金属的轴向作用力变大，成形载荷亦变大，导致模具的使用寿命降低。因此，在实际加工过程中，根据零件的复杂程度以及形状结构，选择合适的凹模入口半角非常重要。

根据花键加工方面的理论知识及实际生产经验，通常认为凹模入口半角在20°～25°范围内比较合适。为了扩大凹模入口半角的优化范围，确定凹模入口半角α的取值范围为15°～30°。

设定凹模入口半角分别为15°、20°、22.5°、25°和30°，利用有限元分析软件DEFORM-3D对花键冷挤压成形过程进行数值模拟，分析不同凹模入口半角对花键冷挤压成形过程的影响。表3为不同凹模入口半角在花键成形过程中的模拟参数值(除凹模入口半角α之外的主要参数)。

表3不同凹模入口半角在花键成形
过程中的模拟参数值
Table3Simulation parameter values of the half angle of different die entrances during spline forming

性能指标数值定径带长度/mm3 摩擦因数0.1 挤压速度/(mm·s-1)16 过渡圆角/mm3

2.1 凹模入口半角对花键成形过程中变形影响

凹模入口半角大小对金属变形有一定的影响，其衡量指标为等效应变。等效应变值越大，则变形程度越大，材料填充效果越好；但变形程度过大，会使变形激烈，从而变形不均匀的可能性变大，导致单位挤压力过大，模具容易发生磨损或破坏。而等效应变值越小，则变形程度越小，变形不均匀的可能性就越小，不会造成模具损坏，但会导致充填效果较差。

图5为花键成形过程中不同凹模入口半角的等效应变云图。由图5a～5e可以看出，不同凹模入口半角下，花键整体的变形层次比较分明，变形较大位置在齿根和齿侧处，即齿根与齿侧处的等效应变值相对较大。凹模入口半角为15°、20°、22.5°、25°、30°时，花键等效应变最大值分别为3.19 mm/mm、2.69 mm/mm、3.28 mm/mm、3.75 mm/mm、4.96 mm/mm。

为了直观反映凹模入口半角与最大等效应变的关系，将不同凹模入口半角对等效应变最大值的影响绘制成折线图，如图6所示。由图6可以看出，凹模入口半角为20°时等效应变值最小，增大或者减小凹模入口半角都会使等效应变值增大。当凹模入口半角小于20°时，一方面坯料与凹模型腔的接触面积变大，造成摩擦阻力增大，从而在一定程度上加大材料变形的不均匀程度；另一方面沿凹模入口半角的分力变大，且远大于摩擦阻力，加快了金属的流动变形，导致材料的变形程度变大，造成等效应变值变大。当凹模入口半角大于20°时，等效应变值开始呈线性关系持续增大，主要原因是随着凹模入口半角增大，模具对坯料的轴向阻力增大，在一定程度上导致变形不均匀程度变大，从而使等效应变值增加。

图5 等效应变云图Fig 5 Equivalent strain cloud map

图6 不同凹模入口半角对等效应变最大值的影响Fig 6 Effect of half angle of different die entrances on the equivalent strain maximum

为了预测和防止实际加工过程中某位置出现金属变形过大导致花键破坏，或某位置变形程度过小导致花键填充效果不好，在凹模入口半角为15°的等效应变云图(图5a)上选取5个关键位置作为取样点进行跟踪分析，研究各个位置变形情况。取样点坐标如表4所示，挤压过程中追踪点等效应变变化曲线如图7所示。由图7可知，位于凹模入口角上面的杆部P1点，在成形过程中等效应变变化值一直为0，说明此处未发生任何变形，因此在生产时可不特别注意此处；位于凹模入口半角与过渡圆角空间曲面交汇处、齿顶位置、花键齿侧与齿根位置的P2、P3、P4、P5点，在成形过程中坯料形状都发生了变化，说明这4处都有一定的变形，其等效应变值变化大小顺序为：P5≈P4>P3>P2，即花键变形程度最大的位置在花键齿侧和齿根位置。由于P2点的应变变化曲线一直增大并未趋于平稳，说明在坯料进入定径带之前P2点变形程度越来越大；P3、P4、P5点曲线均是先增大最后趋于平稳，且均与P2点曲线最大等效应变变化值之间存在一段高度差；位于齿顶位置的P3点在进入定径带后0.06 s左右，基本不再发生变形，位于花键齿侧和齿根位置的P4、P5点在进入定径带后0.1 s左右，基本不再发生变形。显然，花键齿侧和齿根位置的充填效果好于齿顶位置，但是破坏程度却高于齿顶位置；另外，材料超出定径带位置后未出现等效应变值变化的现象，说明成形花键离开定径带后未发生偏移或者弯曲。

综上所述，在填充性良好的情况下，以降低材料发生破坏的可能性为判断依据，建议选择20°的凹模入口半角进行生产加工；为了防止花键出现较大变形程度而使材料破坏，在实际生产中应重点检测花键齿侧和齿根位置的变形程度。

表4取样点的坐标
Table4coordinates of sampling points mm

取样点XYZP13.946770.028411435.5656P24.390320.98381548.3071P36.164522.2439952.1734P44.612091.0253654.5168P51.839912.9461554.9373

图7 挤压过程中追踪点等效应变曲线Fig 7 The equivalent strain curve of the tracking point during extrusion

2.2 凹模入口半角对花键成形过程中金属流动均匀性的影响

凹模入口半角对花键成形过程中金属流动的均匀性有重要影响。一般情况下，凹模入口半角越小，材料流动越均匀；随着入口半角增大，变形区范围也不断变大，金属材料外层与中心层流速的差距变大，金属材料流动越不均匀。在花键挤压成形过程中通常利用速度场来分析金属材料的流动均匀性。速度场是指任一时刻、任一点上的速度矢量组成的物理场，现利用DEFORM软件绘制花键挤压成形过程中不同凹模入口半角的速度场云图(图8)，用于分析不同凹模入口半角下金属流动速度矢量的分布情况，以及金属材料上某点在挤压过程中任一时刻的流动速度矢量变化情况。

图8中箭头方向表示节点所代表单元的金属材料流动方向，其不同的颜色表示速度大小的不同，颜色标尺见图的右侧标注。由图8a～8e可知，在不同凹模入口半角下，花键整体的金属流动规律几乎一致，即花键已成形部位流动速度最大，凹模入口半角位置流动速度次之，杆部位置流动最慢；随着凹模入口半角的增加，挤压结束时速度场最大值基本没有出现明显变化。这是因为金属坯料流过凹模入口半角位置，金属流动方向改变，金属坯料形状发生改变，材料变形空间开始变小；继续下压，同一个凹模入口半角下金属发生变形需要的成形力越来越大，导致金属材料流动速度不断变大。

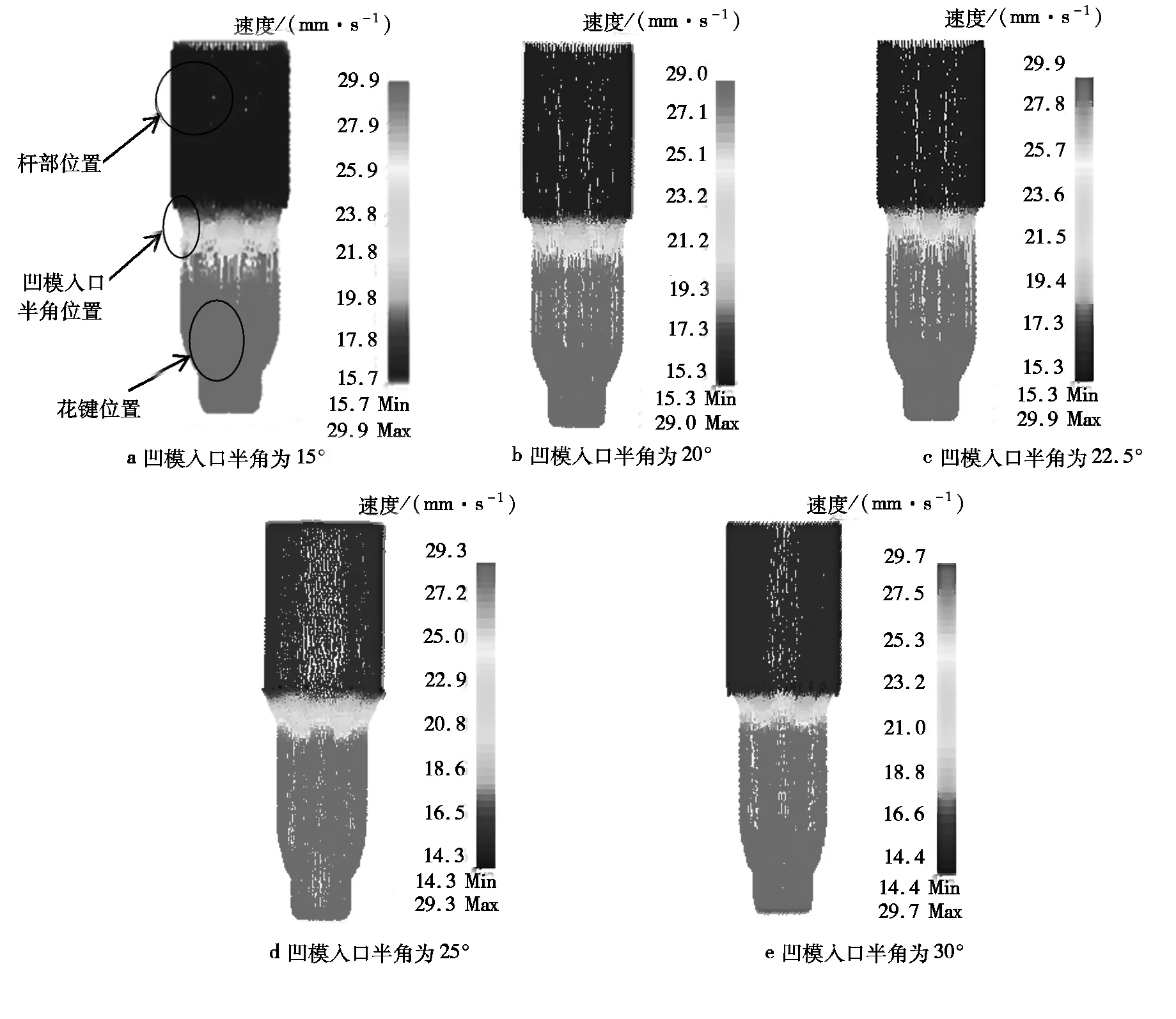
图8 速度场云图Fig 8 Velocity field cloud map

综上所述，不同凹模入口半角情况下金属流速层次都比较分明，流线都非常均匀且都非常紧密；金属流动速度的加剧都是在经过凹模入口半角位置时发生的。故在实际加工过程中最有可能出现金属流动不均匀的位置应该是凹模入口半角位置，需要时常观察该位置的金属流动情况。

2.3 凹模入口半角对花键成形过程中成形载荷的影响

从理论上说，在花键挤压过程中，在一定范围内凹模入口半角越大，成形载荷就会变得越大；但成形载荷过大，会降低模具的使用寿命，导致挤压设备损坏。为了减小成形载荷、提高模具的使用寿命，需对凹模入口半角进行优化，故模拟分析不同凹模入口半角对花键冷挤压成形载荷的影响非常关键。

在DEFORM软件中绘制不同凹模入口半角的花键载荷—行程图，如图9所示。由图9可知：凹模入口半角为15°时，在花键成形过程中凸模与坯料接触后，材料开始发生塑性变形，载荷曲线开始时沿斜线(倾斜45°左右)升高，下压2.8 mm处载荷开始平稳，成形载荷最大值为2.02×104N；凹模入口半角为20°时，材料开始发生塑性变形，载荷曲线开始沿斜线(倾斜60°左右)升高，下压2.0 mm处载荷开始平稳，成形载荷最大值为1.97×104N；凹模入口半角为22.5°时，材料开始发生塑性变形，载荷曲线开始沿斜线(倾斜70°左右)升高，下压1.2 mm处载荷开始平稳，成形载荷最大值为2.06×104N；凹模入口半角为25°时，材料开始发生塑性变形，载荷曲线开始沿斜线(倾斜80°左右)升高，下压1.0 mm处载荷开始平稳，成形载荷最大值为2.23×104N；凹模入口半角为30°时，材料开始发生塑性变形，载荷曲线开始沿纵向直线升高，下压0.4 mm处载荷开始平稳，成形载荷最大值为2.31×104N。由此可见，随着凹模入口半角的不断增加，载荷曲线斜率不断增大，金属材料流动到定径带位置的位移量会变小，成形载荷趋于平稳状态时的距离越来越短。

图9 载荷—行程图Fig 9 Load-stroke diagram

为了更直观地看出凹模入口半角与最大成形载荷的关系，把不同凹模入口半角对最大成形载荷的影响绘制成折线图，如图10所示。从图10可以看出：凹模入口半角为20°时，花键最大成形载荷最小；凹模入口半角大于或者小于20°都会造成最大成形载荷变大。通过分析可知，凹模入口半角大于20°时，随着凹模入口半角的增大，金属流动的路程越短，摩擦力越小，但是在花键成形过程中垂直于凹模入口角的分力却变大，导致最大成形载荷增大；凹模入口半角小于20°时，凹模入口半角过小，材料剪切抗力虽有减小的趋势，但摩擦力会增大，造成总的成形载荷增大。

图10 不同凹模入口半角对最大成形载荷的影响Fig 10 Effect of half angle of different die entrance on maximum forming load

综上所述，若以单一指标降低成形载荷来判断，则凹模入口半角为20°时最大成形载荷最小，模具使用寿命最高，因此建议选用20°的凹模入口半角进行实际生产加工。

2.4 凹模入口半角对花键成形过程中凹模磨损的影响

模具的磨损主要是由于模具与工件之间的摩擦造成的，模具磨损可能会导致模具失效。通常影响模具磨损的主要因素有两个：一个是内部因素，如模具材料的硬度和模具结构等；另一个是外部因素，如润滑情况和下压速度等。在花键挤压成形过程中模具磨损是不可避免的，其中凹模入口半角位置是坯料与模具产生摩擦较大的地方，也是凹模模具结构中磨损面积最大的位置。本节利用DEFORM软件绘制一次挤压结束时不同凹模入口半角的凹模磨损深度分布图(图11)，并以磨损深度为主要判断依据，以模具的表面压强、磨损速度以及滑移速度为辅助判断依据(通常这些数值越小越好)，研究凹模入口半角对模具磨损的影响。

由图11可知，模具磨损的位置基本上都在凹模入口半角和过渡圆角位置，而其他位置磨损则较小。为了更直观地看出凹模入口半角与最大磨损深度之间的关系，用Excel将不同凹模入口半角时的最大磨损深度数据绘制成折线图，如图12所示。由图12可知，随着凹模入口半角的不断增大，凹模最大磨损深度不断增加，但其增长率呈现出越来越小的趋势；在凹模入口半角增大到22.5°后，再增加凹模入口半角，最大凹模磨损深度值基本不再发生较大变化。分析认为，在一定幅度范围内，随着凹模入口半角的增大，金属材料径向流动变形困难，坯料与凹模入口角位置发生较大摩擦，导致模具的磨损深度增加。

图11 一次挤压结束时不同凹模入口半角的凹模磨损深度分布图Fig 11 Depth distribution of die wear at different half angles of die entrance at the end of one extrusion

图12 一次挤压结束时不同凹模入口半角对凹模最大磨损深度的影响Fig 12 Effect of the half angle of different die entrances on the maximum wear depth of the die at the end of one extrusion

模具磨损深度分布图是选取最优凹模入口半角的衡量指标之一，模具磨损深度的不同是多种因素综合作用的结果。为了进一步分析不同位置不同磨损深度产生的原因，在凹模入口半角为15°的凹模模具深度分布图上选取5个磨损较严重的位置点，作为凹模模具追踪点(图11a中的P1、P2、P3、P4、P5，其坐标见表5)，运用DEFORM软件进行数值模拟，并以模具磨损深度、磨损速度、滑移速度、表面压强作为判断指标，绘制挤压过程中模具磨损追踪点曲线图，如图13所示。由图13a可以发现，由于追踪点P1位于进入凹模入口半角的过渡圆角位置，该点最早出现磨损，这是由于金属流动时先经过P1点，之后再依次流过P2、P3、P4、P5点；各追踪点随时间的增加，磨损深度也在不断增加，最终的磨损深度值顺序为P4>P2>P1>P5>P3。由图13b～13d可知，磨损速度值顺序为P4≈P5>P3>P2>P1，滑移速度值顺序为P4>P3>P2>P1>P5，表面压强值顺序为P4>P1>P2=P3>P5。由于P1点位于进入凹模入口半角的过渡圆角位置，P1点的磨损速度和滑移速度均不大，但其表面压强相对较大，显然P1点磨损的原因主要是由于表面压强较大造成的；P2点处于凹模入口半角的靠上位置，该点的磨损速度相对较小，表面压强和滑移速度相对较大，所以P2点磨损的主要原因是由于表面压强和滑移速度较大造成的；P3点在凹模大径与凹模入口半角交汇处，该点的磨损速度和表面压强均不大，但滑移速度相对较大，故P3点磨损的主要原因是由磨损时滑移速度较大造成的；P4点在凹模入口半角底部与过渡位置空间曲面交汇处，此处金属流动最剧烈，因此P4点虽然开始磨损较晚，但是磨损深度却最大，同时P4点的凹模磨损速度﹑滑移速度和表面压强也最大，因此P4点磨损严重的原因是由模具表面压强、磨损速度以及滑移速度共同作用造成的；P5点在圆角与定径带位置空间曲面交汇处，P5点表面压强与滑移速度都最小，但磨损速度却很大，说明P5点的磨损主要是由于凹模磨损速度较大造成的。

表5取样点的坐标
Table5Coordinates of sampling points mm

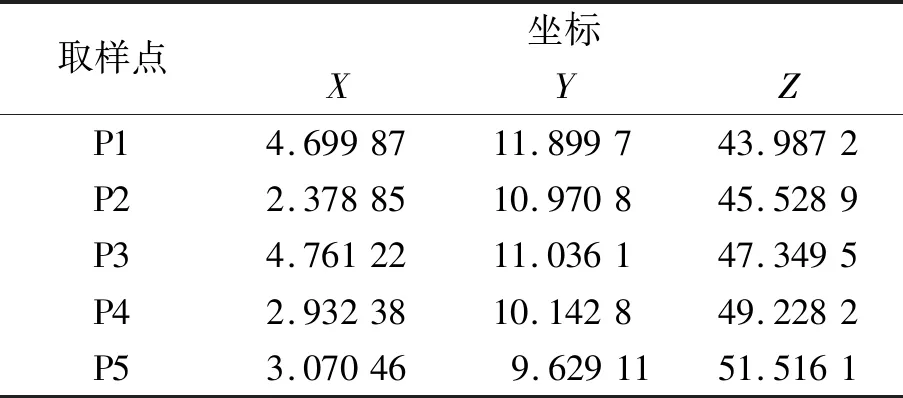
取样点坐标XYZP14.6998711.899743.9872P22.3788510.970845.5289P34.7612211.036147.3495P42.9323810.142849.2282P53.070469.6291151.5161

图13 挤压过程中凹模磨损追踪点曲线图Fig 13 Curve of wear tracking point during extrusion

综上所述，P4点位置凹模磨损相对于P1、P2、P3、P5各点比较严重，因此在实际加工过程中，应重点检查P4点位置的磨损情况，及时修复，尽量减小模具成本的损失。

根据以上讨论可以得出不同凹模入口半角对花键成形质量的影响，如表6所示。由表6可以看出花键成形过程中凹模入口半角为20°时花键成形质量最优，因此在实际生产中建议选用凹模入口半角为20°的模具。

表6不同凹模入口半角对花键成形质量的影响
Table6Effect of half angle of different die entrance onspline forming quality

凹模入口半角等效应变/(mm·mm-1)最大成形载荷/(104N)凹模磨损深度/(10-4mm)成形质量15°3.192.021.06较好20°2.691.971.27最优22.5°3.282.061.31较好25°3.752.231.36较好30°4.962.311.36差

3 总结

基于数值模拟技术，以凹模入口半角为优化参数，以花键成形质量和模具寿命为优化目标，通过设定凹模入口半角分别为15°、20°、22.5°、25°和30°时，模拟分析不同凹模入口半角对花键冷挤压成形过程的影响。模拟结果说明凹模入口半角为20°时，花键的整体成形质量最好，模具寿命较高。同时通过凹模磨损深度分布图对模具磨损较严重的地方进行追踪试验，给出了不同磨损深度产生的不同原因，形成了对磨损机理的有效解释，从而可以在实际生产过程中通过种种方法减少磨损深度，有效提高模具的使用寿命。