雅砻江流域非一致性洪水分析

2019-10-23梁小青纪昌明张验科俞洪杰阎晓冉

水力发电 2019年7期

梁小青，纪昌明，张验科，俞洪杰，阎晓冉

(1.华北电力大学可再生能源学院，北京102206；2.甘肃民族师范学院，甘肃合作747000)

0 引言

洪水频率分析及确定设计洪水是进行水利工程防洪规划及洪水管理的重要依据。随着时间的推移，自然因素和人为因素共同作用，改变了天然洪水的分布规律，不能满足传统洪水频率计算中对洪水一致性的要求。一般情况下，当水文序列的变化规律在一定时期内比较平稳时，认为水文序列是一致的；当水文序列的变化规律在一定时期内发生了变异(具有跳跃性或趋势性的变化)，从一种平稳状态变化到另一种平稳状态时，认为水文序列是非一致的。目前非一致水文序列频率分析的途径主要有还原(还现)和直接计算两种。还原是将变异后的序列修正到变异前状态，还现是将变异前的序列修正到变异后的状态，这两种方法均存在一定缺陷[1- 2]。直接计算的途径有时变矩法、混合分布法、条件概率法等。Strupczewski等[3- 4]最早提出时变矩法，该方法将序列的分布参数表示成时间t的某种函数，是一种从变化趋势角度来分析序列非一致性的方法。混合分布法和条件概率法主要从跳跃变异角度来分析序列的非一致性。混合分布法的基本思想是首先根据序列变异时间点将整个研究序列划分为若干满足一致性的子序列，然后对各子序列的分布函数进行加权综合，得到一个混合分布函数，用以描述整个序列的分布特征。Singh等[5]第一次将混合分布用于非一致性洪水的频率分析，取得了较好的效果。条件概率法[6]的原理是按照洪水物理成因的不同将年内洪水划分为互不重叠的若干时段，由各时段内洪水最大值构成一个样本空间，根据全概率公式可得到发生某一量级洪水的概率。我国学者通过直接计算途径也做了相关方面的研究。王军等[7]应用混合分布估计了淮河流域长系列降雨量的总体分布。刘丙军等[8]利用时变矩法研究了西北江三角洲地区的洪水频率。李新等[9]应用条件概率法和混合分布法分别对王快水库洪峰及三个时段洪量进行了非一致性频率分析。

在洪水频率分析中，非一致性是需要考虑的一个方面；另一方面，洪水是一个复杂的水文事件，具有高度非线性、非平稳性，兼有多个特征属性且各属性之间又有一定的相依性。而传统频率分析是针对单变量进行的；这就使得分析结果不能够全面、可靠地反映洪水事件，给水利工程规划设计或运行管理带来了一定风险。因此，在研究洪水序列非一致性的同时，还需构建以各特征属性为变量的多变量联合分布以较全面地评价洪水事件。传统多变量联合分布构建的前提要求是边缘分布必须为同一类型，而且对于联合分布的类型一般为正态分布，较难求解非正态、多维变量的联合分布。随着1959年现代Copula理论的形成，利用Copula函数求解多变量联合分布的方法被逐渐引入到水文领域。Copula函数不仅对用于构建联合分布的单变量的边缘分布形式没有要求，而且结构清晰，能有效描述水文事件的内在规律和特征属性之间的相互关系[10]，在国内外得到了广泛应用。Grimaldi S等[11]利用非对称Archimedean copula函数建立了洪峰、洪量、历时三变量的联合分布。Papaioannou G等[12]采用Copula函数族求得多瑙河年最大洪峰与多个历时洪量的联合分布。熊立华等[13]用Clayton Copula求得了同一河流上两站年最大洪水的联合分布。李亦凡等[14]通过构造Khoudraji copula求得了干旱历时与干旱峰值的联合分布。李天元等[15]以Gumbel Copula求得了宜昌站最大日流量、7天洪量和30天洪量的三维联合分布。

现有利用Copula函数构建洪水变量联合分布的研究成果，一般为洪峰流量之间的联合、历时洪量之间的联合、洪峰和历时洪量之间的联合等；同时考虑了变量非一致性的成果不多[16]，并且较少将洪水发生时间作为研究变量[17- 18]。雅砻江干流中下游河段是我国十三大水电基地之一。近些年来，下游河段上以锦屏一级为龙头水电站的五级梯级电站的陆续建成，人为改变了天然洪水的时空分布过程，使其不再满足一致性。目前，研究雅砻江流域洪水的文献不多[19- 20]，且缺乏对该流域在变化环境下的洪水进行非一致性分析的相关文献。

针对上述问题，本文将洪水的非一致性与其发生时间联系起来，以雅砻江下游锦屏一级水电站洪水为研究对象，采用混合分布法分析洪水的非一致性，并通过Copula函数求取洪水与其发生日期的联合分布(分析流程如图1)，以便能够掌握锦屏一级水电站洪水与其发生时间的变化规律、二者的组合情况及一定量级洪水发生在不同时间或某一时间发生不同量级洪水的可能性。文中数据处理采用Matlab R2014a、EViews 8等软件。

图1 锦屏一级水电站非一致性洪水分析流程

1 非一致性洪水研究方法

1.1 洪水变量的混合分布

设年最大洪峰流量(或年最大时段洪量)为随机变量X，研究序列年数为N，在序列发生变异的情况下，可用混合分布函数描述其变化特征。即

(1)

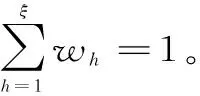
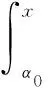
(2)

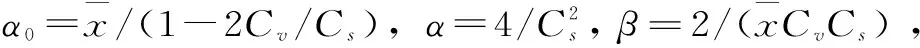
1.2 时间变量的Von Mises分布

设年最大洪峰流量(或年最大时段洪量)发生日期为随机变量Y，汛期天数为n。Di(1≤i≤n)为从汛期开始第i天的日期，通过适当的三角变换，将日期转换为方向数据y后用Von Mises分布函数F(y)表示为[21- 22]

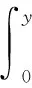
(3)

式中，00；I0(k)为第一类变型Bessel函数零阶值。

日期与方向数据的转换及参数θ0的计算步骤如下：①在一单位圆上选定0°方向位置，从0°方向开始逆时针将日期按时间顺序依次均匀分布在圆周上，则D1，D2，…，Dn对应的圆心角弧度(即方向数据)分别为2π/n，4π/n，…，2π；②确定第j(1≤j≤N)年的年最大洪峰流量(或年最大时段洪量)发生日期在单位圆周上对应点的位置及角度θj；③通过式(4)求arctan(b/a)，并根据a和b的正负，得到角度θ0，对应的日期为年最大洪峰流量(或年最大时段洪量)发生的平均日期。即

(4)

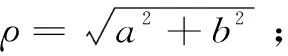
1.3 分布的检验

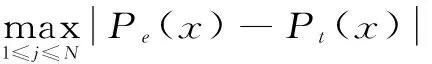
以P-P图法进行边缘分布的拟合效果评价。P-P图法是将变量的经验累积频率与拟采用的分布函数得到的理论累积频率点绘在一张图中，观察点据在45°方向的分布情况，并计算回归系数R2。点据越靠近45°方向，R2越接近于1，表明拟采用的分布函数的拟合效果越好。

2 基于Copula函数理论的两变量联合分布

2.1 Copula函数优选及参数估计

单参数对称Archimedean Copula函数有确定的解析形式，在水文变量频率分析中应用广泛，两变量X和Y的联合分布函数(X≤x和Y≤y同时发生的概率)表示为

F(x，y)=C(u1，u2)=
φ-1[φ(u1;θ)+φ(u2;θ)]

(5)

式中，C(u1，u2)为Copula求得的联合分布函数，u1和u2分别为随机变量X和Y的分布函数F(x)和F(y)；φ(·)为生成函数，φ-1(·)为φ(·)的逆函数；θ为参数。本文选取4种Archimedean Copula函数进行优选，包括Gumbel-Hougaard(GH)、Clayton、Frank和Ali-Mikhail-Haq(AMH)，并采用秩相关系数法[23]估计Copula函数参数θ。

2.2 Copula函数检验

两变量联合分布函数的检验也采用K-S检验的方法，统计量如式(6)，检验过程可参考1.3节。即

(6)

式中，mj是二维观测值为(xj，yj)时，同时满足x≤xj，y≤yj的二维观测值的个数；Cj为观测值(xj，yj)的Copula值。

通过均方根误差(RMSE)法与AIC法[10]对联合分布的拟合效果进行评价。两种方法的指标值越小，说明分布的拟合效果越好。具体为

(7)

(8)

式中，d为Copula参数个数；Pc(·)为Copula联合分布计算值；Pe(·)为联合分布经验值，Pe(j)=(mj-0.44)/(N+0.12)。

2.3 联合超越概率分布及条件超越概率分布

在洪水事件中，通常关注的是指标变量大于某一阈值的概率，为区别于概率论中变量概率分布函数的含义，本文对于两变量X和Y，作如下定义：

联合超越概率分布函数(X≥x和Y≥y同时发生的概率)为

F′(x，y)=1-u1-u2+C(u1，u2)

(9)

条件超越概率分布函数(给定X≥x时，Y≥y发生的概率或给定Y≥y时，X≥x发生的概率)为

F′Y|X(y|x)=[1-u1-u2+
C(u1，u2)]/(1-u1)

(10)

F′X|Y(x|y)=[1-u1-
u2+C(u1，u2)]/(1-u2)

(11)

根据2.2节优选出的Copula函数可求得上述各函数值。

3 实例分析

3.1 研究区概况及数据资料

雅砻江流域水能资源极其丰富，干流下游规划有锦屏一级、锦屏二级、官地、二滩和桐子林5座水电站。其中，由锦屏一级、锦屏二级、官地构成的“锦官电源组”为国家电力调度控制中心直调电站，锦屏一级为控制性电站，是一座以发电为主，并兼有分担长江中下游地区防洪任务的年调节电站。

锦屏一级水电站水库正常蓄水位为1 880 m，正常蓄水位下水库库容为77.6亿m3，属于大(1)型水利枢纽工程。考虑到大型水库的调节性能高，其防洪调度主要通过洪量进行控制。因此，本文依据锦屏一级水电站1972年～2010年入库洪水的年最大时段洪量来分析洪水的非一致性。经数据资料审查，满足可靠性和代表性要求。

3.2 年最大时段洪量非一致性分析

3.2.1变异点的确定及显著性检验

采用累积距平法[24]对锦屏一级水电站年最大1日洪量序列和年最大3日洪量序列的变异情况进行定性分析(见图2)。

爸跟我说：“你妈走了，我怎么办？”爸的头发一下子全白了。我感觉他不是以前那个老爸了。终于，有一天，他也病了，也是肾结石。我们一家都有肾结石，可能是水的原因。老秦给他配了草药，说老人年纪大了，最好保守治疗，用草药给化了。可是草药没有见效，爸疼得喘不上气。老秦说，不能再拖了，赶快住院做手术。

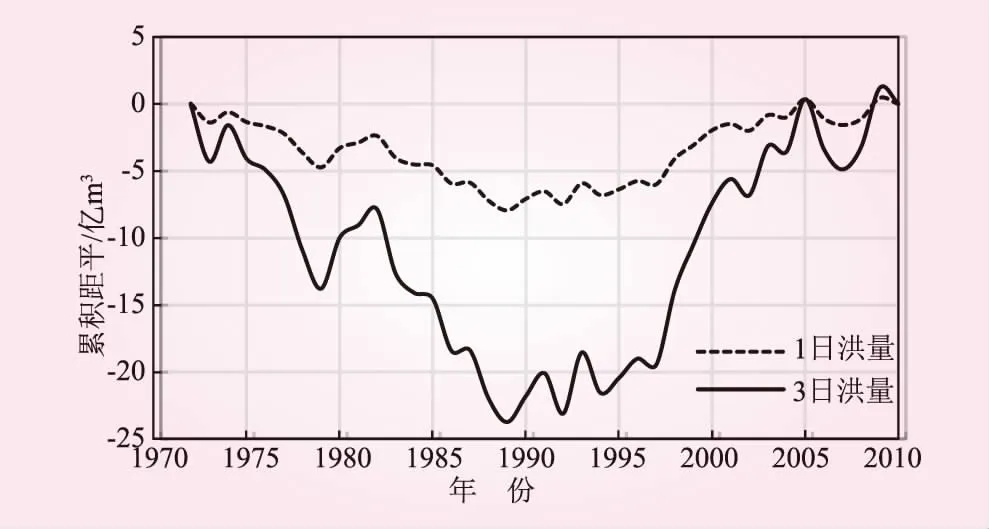
图2 年最大时段洪量累积距平过程

根据宋松柏等人的建议[25]，考虑将序列分成两段；因此，在图2中年最大1日洪量序列、年最大3日洪量序列的累积距平过程曲线上，均取最小极值点对应的年份1989年作为可能变异点来进行研究。

采用滑动t检验法[26]对1989年变异显著性进行定量分析。在1989年前后分别获取步长为10a的子序列，检验结果见表1。

表1 年最大时段洪量滑动t法检验结果

注：显著性水平α为0.1时，临界值为1.734 1。

由表1可知，年最大1日洪量序列和年最大3日洪量序列在1989年均发生显著变异，两个时段洪量序列均存在非一致性情况。下面以年最大1日洪量为例，说明非一致洪水频率与当前设计频率的差异。

3.2.2子序列及平稳性检验

将年最大1日洪量序列以变异年份1989年划分为1972年～1989年和1990年～2010年两个子序列。检验序列是否平稳的方法有时序图法、样本自相关函数法及单位根法等。其中，单位根法中的ADF检验[27]是目前应用较多且最为有效的。本文采用ADF检验法对子序列进行平稳性检验(见表2)，显著性水平取0.05。

表2 子序列ADF检验结果

由表2可知，通过ADF检验得到两个子序列不平稳的概率均小于显著性水平，可认为两个子序列是平稳和一致的。

3.3 非一致年最大1日洪量及其发生日期的分布

将年最大1日洪量作为洪水变量X，设1972年～1989年和1990年～2010年两子序列的分布函数分别为F1(x)和F2(x)。选取一年中的6月1日～9月30日为汛期，年最大1日洪量发生在汛期的日期为时间变量Y。两子序列分布参数、当前设计分布参数及年最大1日洪量发生日期分布的参数计算结果见表3。取显著性水平α为0.05，年最大1日洪量与其发生日期的K-S检验结果见表4。

将两变量各自分布的经验频率和由式(1)～式(3)得到的对应理论频率点绘于图3中。由图3a和图3b可知，各点在45°方向分布均匀，回归系数R2均在0.95以上，理论分布均拟合较好。

另外，本文将考虑变异的混合分布曲线、当前设计分布曲线、经验频率点据置于同一图中(见图4)。由图4中曲线拟合情况可知，混合分布曲线与经验频率点据在整体上拟合较好，特别是频率较小的中上部，而当前设计分布曲线只对频率大于20%的点据拟合较好，说明混合分布模型较当前设计分布合理。

3.4 Copula函数优选及两变量联合分布

经SPSS软件分析得到年最大1日洪量与发生日期两变量的Kendall秩相关系数τ为0.118，可知二者为正相关关系，各Copula函数参数、统计量及拟合指标值计算结果见表5。

由表5可知：4种Copula函数的K-S检验统计量Z值都小于临界值0.218，均通过检验；但Clayton Copula的统计量值最小，检验结果最为显著。从拟合指标值来看，RMSE值和AIC值最小的也是Clayton Copula。Clayton Copula也适合构造具有正相关关系的变量之间的联合分布[17]。

图3 非一致年最大1日洪量及发生日期示意

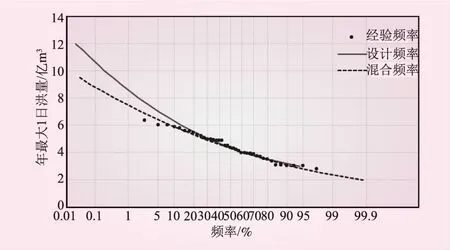
图4 不同分布拟合效果

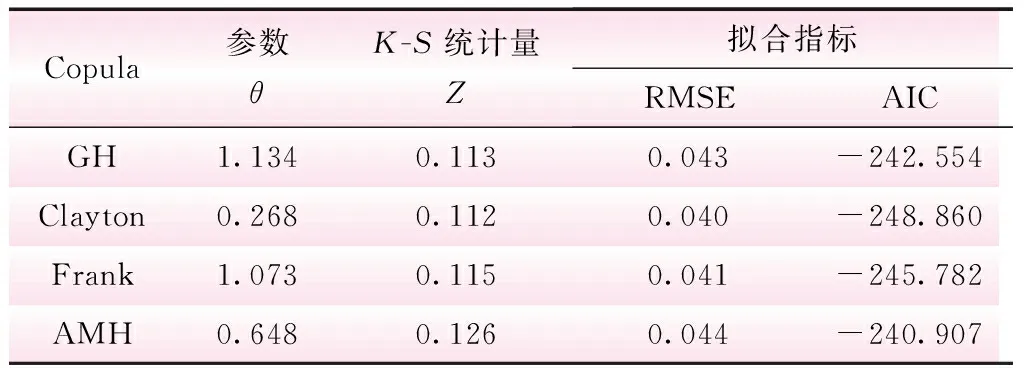
Copula参数θK-S统计量Z拟合指标RMSEAICGH1.1340.1130.043-242.554Clayton0.2680.1120.040-248.860Frank1.0730.1150.041-245.782AMH0.6480.1260.044-240.907

综合上述考虑，本文以Clayton Copula函数来构建非一致年最大1日洪量与其发生日期的联合分布，并求得联合超越概率分布，其三维曲面图和典型概率等值线图如图5、6所示。

由图5，一方面可得到超过某一量级洪水发生在不同日期后的概率及发生在某时间段的概率。如，W≥2.5亿m3的洪水在6月4日后发生的概率为96.4%，在7月1日后发生的概率为83.2%；则发生在6月4日～7月1日之间的概率就是13.2%。另一方面，也可得到某一日期后发生超过一定量级洪水的概率及发生某一量级段洪水的概率，如，8月10日后发生W≥2.8亿m3洪水的概率为42.8%，发生W≥4.25亿m3洪水的概率为25.8%，则发生2.8～4.25亿m3洪水的概率为17%。

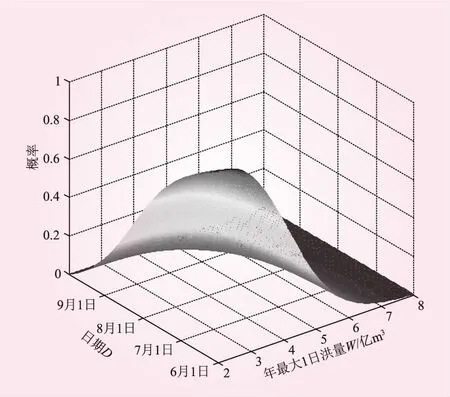
图5 联合超越概率分布

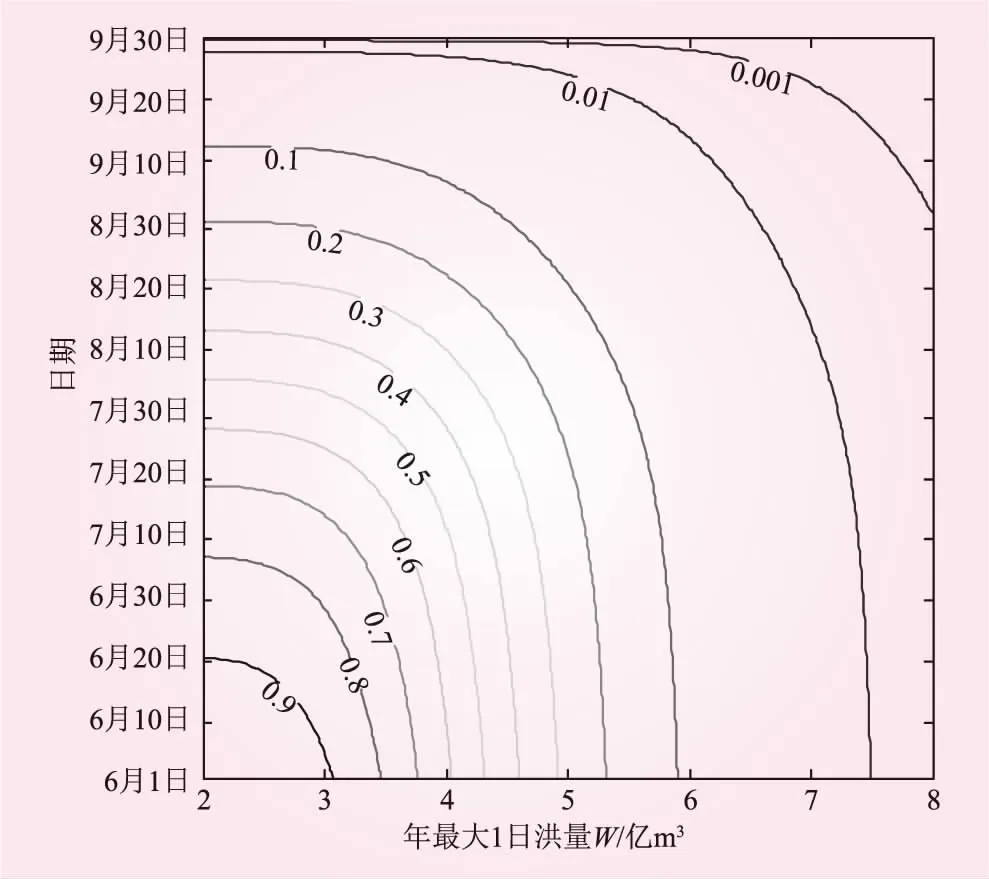
图6 联合超越概率分布等值线

由图6中等值线可得到给定某一概率时，洪水与其发生日期的不同组合情况。另外，等值线的疏密程度说明了洪水发生的可能性大小，等值线越密，发生的可能性越大。由图可知，纵坐标轴上7月20日～8月20日的等值线较密集，对应横坐标轴上洪水的等值线分布也较密，说明该电站较容易在7月下旬到8月下旬这个时间段内发生3.5亿～5亿m3大小的洪水。

3.5 条件超越概率密度

根据式(10)～(11)可得到Clayton copula函数的条件超越概率密度

(12)

(13)

图7a、7b中各绘制了3条非一致年最大1日洪量和发生日期的条件超越概率密度曲线，其中图7a为给定洪水量级X的情况下，发生在日期Y后的条件概率密度曲线，图7b为给定日期Y的情况下，发生超过X量级洪水的条件概率密度曲线。

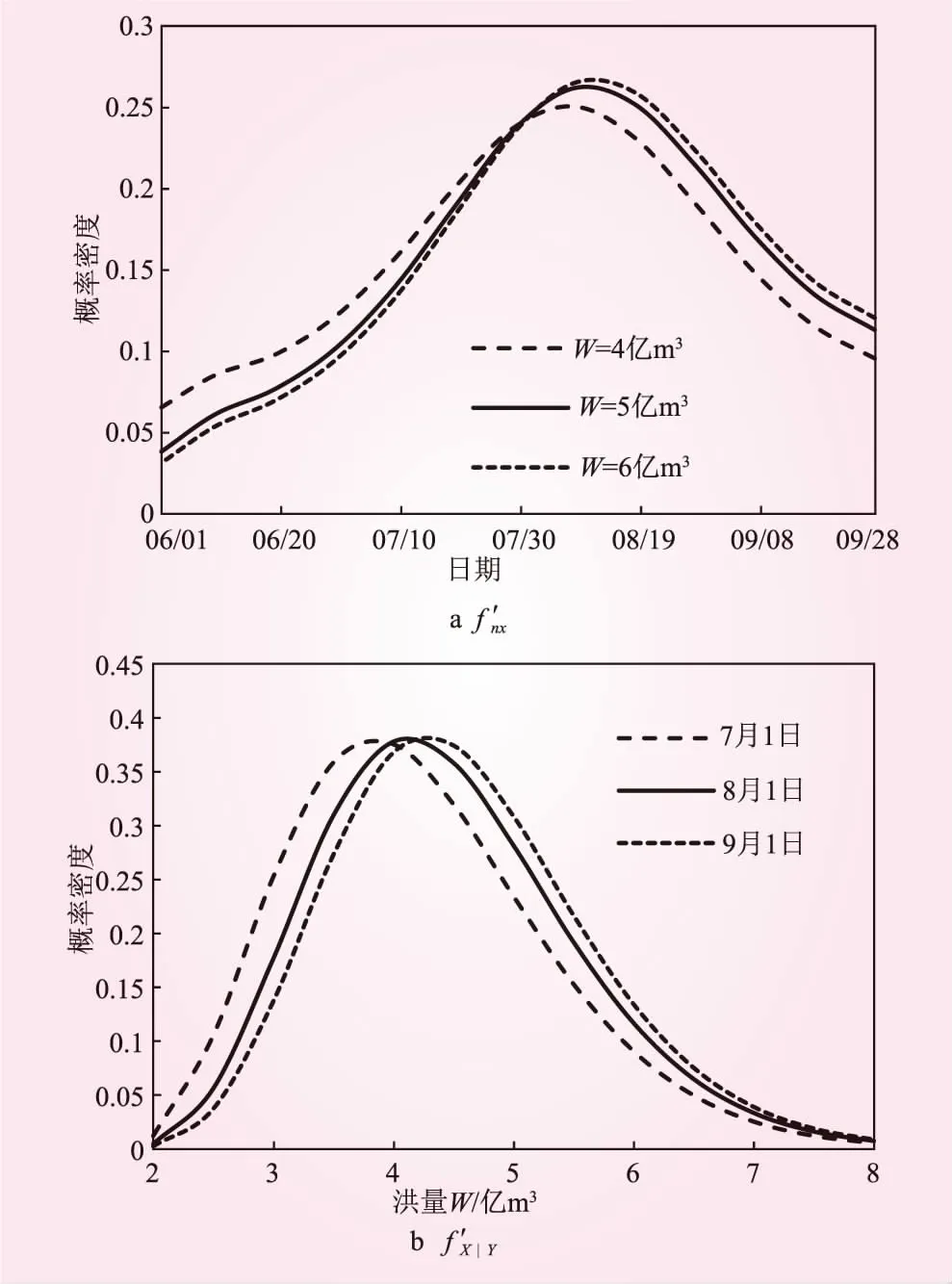
图7 条件超越概率密度

图7a中不同量级洪水发生的概率密度均随着日期的向后推移呈先增大后减小的变化趋势；曲线最高点处的概率密度反映了年最大1日洪量发生在对应横坐标日期附近的概率也大。如，4亿m3量级洪水的条件超越概率密度最大值为0.251，说明该量级洪水发生在8月9日左右的可能性最大。根据各曲线较大概率密度所在范围，得出锦屏一级水电站的主汛期在7月19日～8月30日左右，这与实际情况相一致。前汛期小量级洪水发生的概率大于大量级洪水发生的概率，主汛期和后汛期的情况与前汛期相反。同理，图7b中不同日期发生洪水的概率密度均随着洪水量级的增加呈先增大后减小的变化趋势；曲线最高点的概率密度反映了在该日期发生对应横坐标量级左右洪水的概率最大。如，9月1日最有可能发生4.5亿m3量级左右的洪水。