城市街谷与上游阻挡建筑最不利间距的研究

2019-10-23周华元亢燕铭刘改玲

中国环境科学 2019年10期

周华元,亢燕铭,杨方,刘改玲,钟珂

城市街谷与上游阻挡建筑最不利间距的研究

周华元,亢燕铭,杨方,刘改玲,钟珂*

(东华大学环境科学与工程学院,上海 201620)

采用数值模拟的方法,研究了街谷内上风建筑与上游阻挡建筑的间距(),即上游建筑间距,对街谷内空气流动特性和气态污染物分布规律的影响.模拟结果表明,街谷内迎风区的气流速度基本不随的变化而变化,而背风区和中心区的气流速度随着的增加呈现先减小后增大的趋势,并在= 90m时,气流速度达到最小值.相应地,在= 90m时街谷内污染物浓度最高,表明存在最不利值,在城市规划中应尽可能避免该间距.当大于90m时,越大,污染物浓度越低,而小于90m时,越小,污染物浓度也越低,可以同时实现节约用地和减小交通污染的目的.

街道峡谷；上游阻挡建筑；交通污染物；间距；数值模拟

随着我国机动车保有量的不断提高,机动车尾气对城市居民健康的威胁日益增大.特别是近年霾污染治理过程中,交通污染被列为主要原因之一[1].为便于交通污染物快速扩散,在我国近年的城市规划中,尽可能在建筑物之间设置公共绿地,增大部分街道峡谷(以下简称“街谷”)两侧相邻建筑的间距,给居民提供更好的空气品质.考虑到城市区域土地紧张的现状,这种措施不仅实施难度大,而且也没有数据结果证明其有效性.

关于街谷微环境,在过去的三十余年里,已经开展了大量的研究工作.大致可以分为两类.一类主要关注传统街谷内部气流细节特征和污染物浓度分布的研究[2-9],如Hunter等[2]分析了街谷尺寸对街谷中涡流形态的影响.董龙翔等[3]对地面点源释放的污染物在城市中的扩散过程进行了数值模拟,并通过敏感性数值试验定量分析了边界入口风速和风向扰动对城市内流场和污染物扩散的影响.另一类则针对街谷约束物,如高架道路、绿化带和树冠等对街谷内流场和污染物扩散的影响进行分析[10-16],如Zhang等[10]讨论了高架桥下深街谷内流场和污染物分布的特征,Ng等[11]采用数值模拟的方法研究了不同高宽比下植被对孤立深街谷内空气质量的影响.

然而,现有大部分工作的研究均针对孤立街谷展开.实际上,在城市中街谷不是孤立存在的,建筑之间公共绿地的尺寸和上游阻挡建筑的存在显然会对下游街谷内的流场产生影响.对此,有人对上游阻挡建筑对街谷来流的阻挡作用进行了研究[17-19].如朱强等[17]研究了不同上游阻挡建筑布局下,行列式和错列式街谷内气流速度和污染物浓度场特征.结果表明,在行列式街谷中,若不考虑上游阻挡建筑的存在,将会过高估计街谷内污染程度.因此,上游阻挡建筑对街谷来流的阻挡作用不能被忽视.并且可以推测,上游阻挡建筑与街谷上风建筑的间距(),也会对街谷内的污染物分布产生一定的影响.为更加准确地预测街谷内空气环境质量并为城市规划设计提供参考依据,本文将对此展开研究,以分析可能存在的的最不利取值.

本文拟采用计算流体力学的方法,根据已有实验研究[20-23]及其实测结果选择合适的湍流模型,运用验证后的数值计算方法,以上游阻挡建筑与街谷上风建筑的间距为变量,研究其对街谷内部流场和浓度场的影响.

1 计算模型与方法

1.1 模型建立与计算方法

街谷两侧都会有相邻建筑,其中下游相邻建筑对街谷内的气流形态的影响可以忽略不计,故本文仅研究上游相邻建筑(以下简称“上风建筑”)对来流的阻挡作用及其对街谷内部气流和污染物扩散特征的影响.

图1是本文建立的街谷模型示意.为保证结果的普适性,本文以规则的多层建筑物为研究对象,通过CFD数值模拟,对街谷两侧的建筑物高度均为20m的情况进行分析.设临街建筑和上游阻挡建筑的几何参数均为长60m (),宽15m (),高20m (),街谷同侧相邻建筑的间距为10m (),街宽为30m (),上游建筑间距为.临街建筑沿街谷长轴方向周期性排列.为了更广泛地分析上游阻挡建筑与街谷上风建筑的间距对街谷内空气环境的影响,本文中在15~200m范围内,按一定规律取10个值,用以分析对交通污染物分布规律的影响.

图1 街谷模型示意

使用Gambit 2.4.6软件建立模型和划分网格,使用Fluent 6.3.26软件对计算域内流场(包括风速与湍流强度)和污染物浓度场进行三维数值模拟.为尽量减小因求解域有限产生的端部效应,上游阻挡建筑与计算域上游边界相距5,街谷下风建筑与计算域下游出口相距15,建筑顶端与计算域上方自由面相距4[24].

已有研究[25]表明,街谷中进行数值模拟计算,标准-模型适合作为湍流模型,并采用有限容积法离散控制方程[26-27],采用二阶迎风差分格式控制方程离散[28],污染物的扩散方程采用QUICK格式.离散化计算域后总网格数约有3.3´106个.有关流动与污染物输送的控制方程,其网格稳定性、可靠性分析与描述方法以及其他参数选取的细节参见文献[29].

风向对街谷内的流场影响很大,进而影响街谷内污染物的扩散.当风向与街谷轴线垂直时,最不利于交通污染物的扩散[30].因此,本文仅考虑来流风向与街谷轴线垂直的情况.此时,街谷内流场分布呈周期性变化规律,可采用镜像法在街谷两侧设置对称面(Symmetry),简化计算,只需计算图1(街谷模型)中灰色区域.

计算域的其他边界条件设置如下:计算域内的建筑表面及街谷地面设为无滑移条件,而求解域的顶面设为滑移条件[28].因计算域出口的空气流态可视为充分发展湍流,故出口边界条件可设为自由出流(Outflow).入口边界条件设置为速度入口(Velocity Inlet),并采用用户定义函数(UDF)设置自定义速度廓线.自定义速度廓线设置如下.

大气中风的湍流特性及风速的垂直分布与地形、地面的粗糙度密切相关[18].因此,本文采用幂指数的风速廓线[31-32]

式中:为任意高度,m;z为该高度下的速度平均值,m/s;为地面粗糙度指数,本文取= 0.28;为参考标准高度,m;V为高度处所测的参考标准风速,m/s,定义建筑物高度20m为参考标准高度,则高度=20m处的屋顶风速为参考标准风速V.为模拟近地面处不利的大气扩散条件下街谷空间中交通污染物分布情况,设置屋顶风速为V=2.0m/s,易估得求解域的Reynolds数的量级为105.

街谷空间内的污染源可视为连续发散的线源[33],污染物均匀分布在一个宽10m、高0.5m,长度与求解域相同的区域内,并位于街谷街道正中.污染物气体设为机动车的尾气主要成分CO.为更直观明了地进行分析比较,定义无量纲浓度C表征交通污染物浓度:

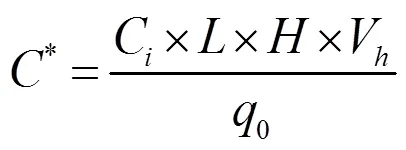
式中:C为点处的污染物浓度,kg/m3;0为污染物发散强度,kg/s.

1.2 数值计算方法的合理性验证

数值计算之前,首先需要对模型和计算方法进行合理性验证.

1.2.1 流场的验证在已发表的实验结果中,与本文特征最接近的是Li等[20]的水槽实验, 因此本文利用该水槽实测数据对计算模型进行验证.

图2给出了街谷两侧建筑1/2高度处(/= 0.5)水平方向和垂直方向的无量纲速度分量沿街道宽度方向的变化曲线.另外,图中还给出了Liu等的LES模型[21]和Li等的标准-模型[22]的模拟结果.

(a) 水平速度分量

(b) 垂直速度分量

图2 流场模拟值与实测值的比较

Fig.2 Comparisons of simulated velocities with test data in street canyon

由图2可以看出,本文与另外两篇文献的模拟结果都与实测数据吻合较好,其中均采用标准-模型的本文和文献[22]的计算结果更接近实测结果,表明本文选择的湍流模型适当,采用的数值计算方法可以较准确地预测街谷内流场.

1.2.2 浓度场的验证除流场的验证外,本文的数值模型还需要对街谷内的污染物浓度场进行验证.本文采用Meroney等[23]的风洞实验结果进行比对和校验,分别验证了入口风速为ref= 3m/s和ref= 5m/s的情况,结果如图3所示.

(a) Vref = 3m/s (b) Vref = 5m/s

图3 浓度场模拟值与实测值的比较

Fig.3 Comparisons of simulated concentration with test data in street canyon

图3的结果表明,尽管实测值与模拟值之间存在一些差异,但两者的变化规律基本相同,大部分模拟值与实验值吻合较好.

从上述验证的过程来看,本文选择的数值模型和数值计算方法能较好地预测街谷内的流场和速度场.

2 模拟结果与分析

2.1 上游建筑间距D对街谷内气流特征的影响

图4(a)和(b)分别给出AA’横剖面(图1)上街谷内气流速度矢量图和湍流强度分布云图.从图4(a)中的流场可以看出,街谷上风建筑的迎风侧在无上游阻挡建筑时,街谷上风建筑附近的气流由地面吹向屋顶;而在有上游阻挡建筑情况下风向相反.由于此风向的不同,导致街谷内部形成的涡流形态和风速有一些差别.前者在街谷内产生了一个较小的涡,靠近上风建筑和下风建筑处的风速较大;而后者产生了一个较大的涡.不仅如此,在不同的下,街谷内涡的位置和大小也有一定区别,这些区别会对交通污染物的扩散有一定的影响.从图4(b)可以看出,虽然在无上游阻挡建筑时,上风建筑的迎风侧上端湍流强度最大;在有上游阻挡建筑时,该处湍流强度有所减小,但是街谷内较低位置的湍流强度却基本无变化.

(a) 气流速度

(b) 湍流强度

图4 街谷横剖面AA’ (= 15m)上的流场

Fig.4 Flow fields on plane AA’ (= 15m) in street canyons

为更加具体地比较对街谷空间空气流动状态的影响,图5给出中心区3个典型位置处(图1)气流速度沿高度方向分布的情况.

由图5(a)可以看到,在6m高度以下,= 200m时街谷内气流速度较其他间距小,= 75m时街谷内气流速度最大.而在6m高度以上,= 200m时街谷内气流速度反而最大,因此对街谷内的流场有一定影响.由图5(b)可以看到,对位置2的影响作用较小,不同的对应的气流速度在各高度处基本相同.

图5 街谷中典型位置处气流速度沿高度方向分布曲线

另一方面,有上游阻挡建筑时,3个考察点的速度分布的最小值都出现在街谷内部,最小值出现的高度因考察点位置不同而不同,并受到的影响.无上游阻挡建筑时,速度最小值出现位置高度受考察点位置影响非常大.

湍流强度也是影响流场的主要因素之一,图6给出了中心区3个典型位置处(图1)湍流强度沿高度方向分布的情况.

从图6可以看到,无上游阻挡建筑下3个考察点的湍流强度均比有上游阻挡建筑下的湍流强度小.有上游阻挡建筑的情况下,各个位置处湍流强度的规律基本相似,且都在近地面处增加的幅度较其他高度处大.虽然湍流强度在数值上稍有不同,但变化规律不随的变化而变化,因此下文将主要分析街谷内风速随的变化规律.

为了统计分析上游阻挡建筑与街谷上风建筑的间距对街谷内气流和浓度分布的影响,本文在街谷空间内均匀设点.相邻取值点间距为1m,最边缘处的点距建筑壁面或地面0.5m,取值区域的划分见图7中灰色的区域.

图6 街谷中典型位置处湍流强度沿高度方向分布曲线

图7 街谷内平面区域划分

根据CFD模拟结果,得到每个取值点的信息,图8给出3个区域内气流速度的统计结果.

图8 街谷内气流速度的统计结果

图8(a)和(b)表明,在街谷的背风区和中心区,气流速度受到的影响较大,且都在= 90m时气流速度达到最小值.而在迎风区(图8(c))中,气流速度受到的影响较小,不同的下气流速度基本没有变化,但气流速度在60~135m范围内也存在最小值.

比较图8的统计结果可以看出,无论为何值时,有上游阻挡建筑的街谷内气流速度都比无上游阻挡建筑的街谷内气流速度要小,这将导致污染物扩散不畅,影响街谷内的空气品质.

为明确对街谷内气流速度的改变作用,定义街谷内气流速度的下降率为:

式中:为空间高度下的气流速度下降率;为空间高度下的平均风速;0i为无上游阻挡建筑情况下的平均风速.

图9给出了相对于无上游阻挡建筑时,在不同下街谷内气流速度的下降率.可以看出,上游阻挡建筑的存在会使街谷内的风速下降30%~50%,且在75m时下降率达到最大值.相比于中心区和迎风区,背风区风速下降率高出5%~10%左右.

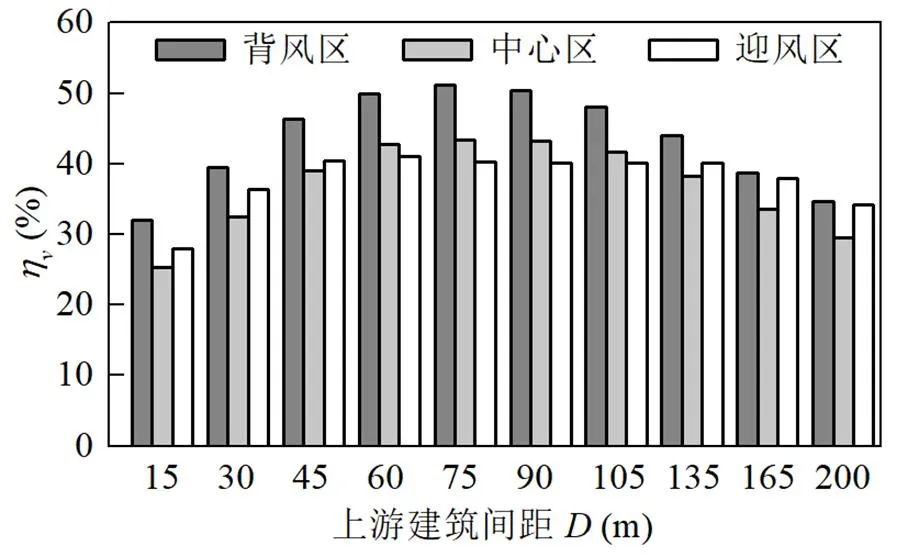
图9 不同D时街谷内气流速度下降率

上游阻挡建筑对街谷内气流速度的影响将会影响到街谷内机动车污染源的扩散特征.以下将对街谷内污染物浓度分布进行分析.

2.2 上游建筑间距D对污染物浓度分布的影响

图10给出了AA’横剖面(图1)的街谷污染物分布和流线.

从图10(a)可以看出,无上游阻挡建筑时,污染物在涡流的作用下主要堆积在街谷背风区建筑附近和中心区近地面.当45m(图10(b))时,污染物向街谷中心区的涡流中心聚集.而当增大到200m (图10(c))时,污染物又向街谷背风区的地面以及街谷空间聚集.

图10 街谷横剖面AA’(x = 15m)上的浓度场

造成以上区别的原因是不同的对应的流场不同.当上游阻挡建筑距离街谷较远(如图10(c))时,上游阻挡建筑对来流的阻挡作用接近于无上游阻挡建筑的情况,因此浓度场又近似于无上游阻挡建筑的情况,向街谷背风区的地面聚集.

根据图7中划分的三个区域,从数值模拟结果中提取相应区域的污染物无量纲浓度,统计结果如图11所示.

图11 街谷内污染物无量纲浓度统计结果

对比图11可以看出,背风区污染物浓度最高,迎风区污染物浓度最低.这是由于街谷中形成了顺时针涡流,迎风区得到的是新鲜空气,因此污染物浓度最小;而背风区得到的是受污染空气,因此污染物浓度最大.

另外,在背风区(如图11(a))中,虽然不同下风速变化较大,但由于处在污染源下游,直接受到污染物的扩散影响,污染物浓度在各下基本一致,不受大小的影响.而在迎风区(如图11(c))中,虽然风速在各下基本一致(图8(c)),但由于受到中心区回流的影响,中心区风速在= 90m处存在风速最小值,因此污染物浓度在= 90m处存在一个最大值.

为估算其他上游阻挡建筑与街谷上风建筑的间距下交通污染物的浓度,采用Origin程序拟合3个区域内污染物浓度的平均值,拟合采用三次多项式: