轧机油膜轴承试验台轴承参数优化分析

唐雪锋，王建梅，侯定邦

(太原科技大学 重型机械教育部工程研究中心,太原重型机械装备协同创新中心，太原 030024)

油膜轴承作为一种特殊的滑动轴承，具有调速范围广、抗冲击能力强、承载能力大，摩擦损耗低等特点[1]，更是作为钢铁冶金、航空航天、矿山机械设备的关键零部件，对它的研究深度，在一定程度上反映了国家高精尖领域的科研实力。随着生产技术和要求的提高，新建的钢厂使用的轧机正向着高速重载的方向发展，传统的油膜轴承已经不能很好的适应这样的工况，经常发生各种问题，有时甚至影响了带材的表面质量，严重制约着钢铁行业的发展。在这样的背景条件下，全球的油膜轴承制造厂、专家学者、科研单位都进行了有关高速、重载动压油膜轴承设计改造的研究工作，既提高轴承在冶金设备的应用水平，也促进了对其的理论研究[2]。轧机油膜轴承试验台是大型机电液气一体化设备，能够有效的模拟实际生产中油膜轴承的运行情况，为轧机油膜轴承提供有效的实验数据[3]。在轧钢设备当中，轧辊油膜轴承性能的好坏直接影响了产品质量，因此通过改进试验台油膜轴承参数，优化其工作性能，这能够有效地提高使用寿命，减少停机次数，增加经济效益。

1 轴承参数优化设计数学模型

1.1 现有条件及参数

以油膜轴承试验台试验轴承为研究对象[4]，试验轴承处于悬置式工作状态，其已知工作条件如图1所示、轴承具体参数如表1所示。

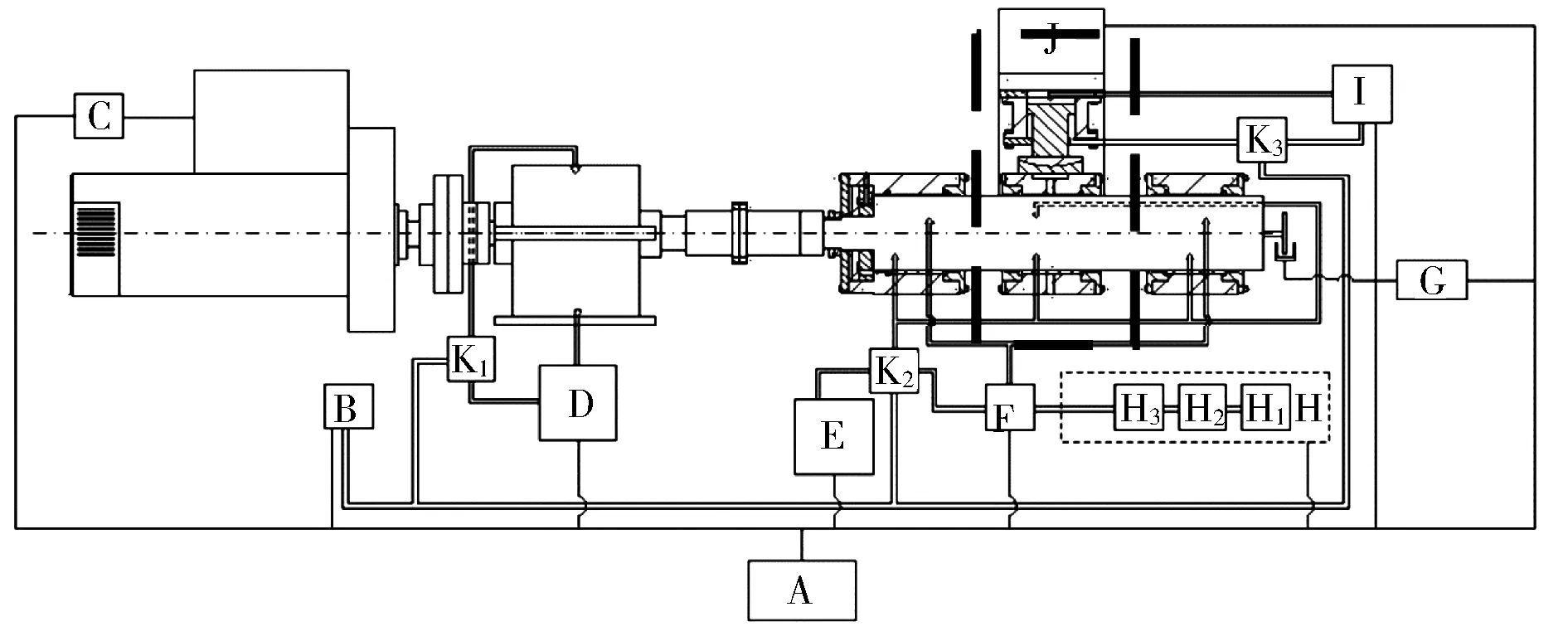
图1 油膜轴承试验台Fig.1 Oil film bearing test bench

1.2 确定设计变量和建立目标函数

对于轧机油膜轴承而言，需将其承受载荷的能力以及工作时的性能优劣当作目标函数。判断标准[5]应该囊括承载能力系数函数f1x、摩擦系数函数f2x和发热量函数f3x.

表1 工作参数表
Tab.1 Working parameters

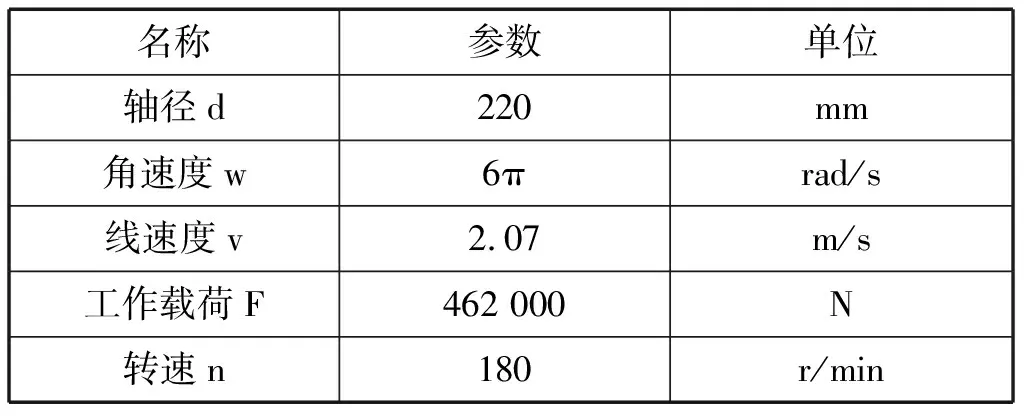
名称参数单位轴径d220mm角速度w6πrad/s线速度v2.07m/s工作载荷F462 000N转速n180r/min

油膜轴承运转时主要的参数为：宽径比B/d，相对间隙ψ，润滑油粘度系数η，由此可得轴承优化设计变量:

X=B/d，ψ，η=x1,x2,x3

设目标函数为Fx，将单一目标函数求得的优化解作为加权因子，凭借线性加权法得到多目标函数[6]：

Fx=N1f1x+N2f2x+N3f3x

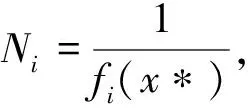
承载量系数函数：

摩擦系数函数：

轴承发热函数：

1.3 建立约束条件

油膜轴承承载能力会随着油膜厚度的减小而增大，当膜厚处于微米级别时，会受到轴径表面和衬套内表面粗糙度的双重影响，同时还受材料弹性变形和热变形的影响，多因素情况下的hmin约束条件为：

轴承宽径比约束条件：

g2x=x1-(B/d)max≤0；

g3x=(B/d)min-x1≤0；

轴承比压约束条件：

按照轴径尺寸选择相对间隙约束条件：

g6x=x2-Ψmax≤0；

g7x=Ψmin-x2≤0；

润滑油选择320风力发电设备传动系统专用油，t=40 ℃～60 ℃时的粘度约束条件：

g8x=x3-ηmax≤0；

g9x=ηmin-x3≤0；

k—考虑误差的安全系数，一般2～3，Rz1、Rz2轴径和衬套内孔表面粗糙度十点高度。

2 基于MATLAB工具箱的遗传算法

J.Holland教授由生物进化理论的思想获得启发，通过整个进化过程基因的遗传与染色体的改变提出了一种随机化搜索方法即遗传算法[8]。此方法在没有任何约束下也可以主动的得到和引导优化的搜索方向，可以用来解决庞大和非线性的问题。它的原理在于：确定某个已知优化问题的初始值，进行自动搜索后，相互的个体间会传递不同信息，将最终得到的解设定为一个群，群当中的个体看做生物的染色体，不同个体根据物竞天择，淘汰弱者的规律开始进化，通过一系列选择、遗传、变异等机制又生成新的个体，经过多代筛选最终得出条件最优的个体[9]。

2.1 求解步骤

根据生物遗传原理，寻求某个问题的优化解就如同寻求种群间的最优个体。首先需要无规则的产生M个个体作为初始种群，组成种群的每个个体需要确定在其范围内基因的优劣情况，这里用适应度值来评判。然后按照优胜劣汰原则，选择适应度值高的个体进行遗传操作即进行交叉变异，它们会以一定的概率生成后代，后代之间通过信息传递又会组成新的种群，此时再次评判其基因的优劣，赋予优选个体新的适应度值并展开循环，直到基因条件满足预先设定的停止准则，最终输出得到最优的个体，最优个体代表了某个问题所寻求的最优解。基于以上法则，遗传算法下的生物进化流程如图2所示。

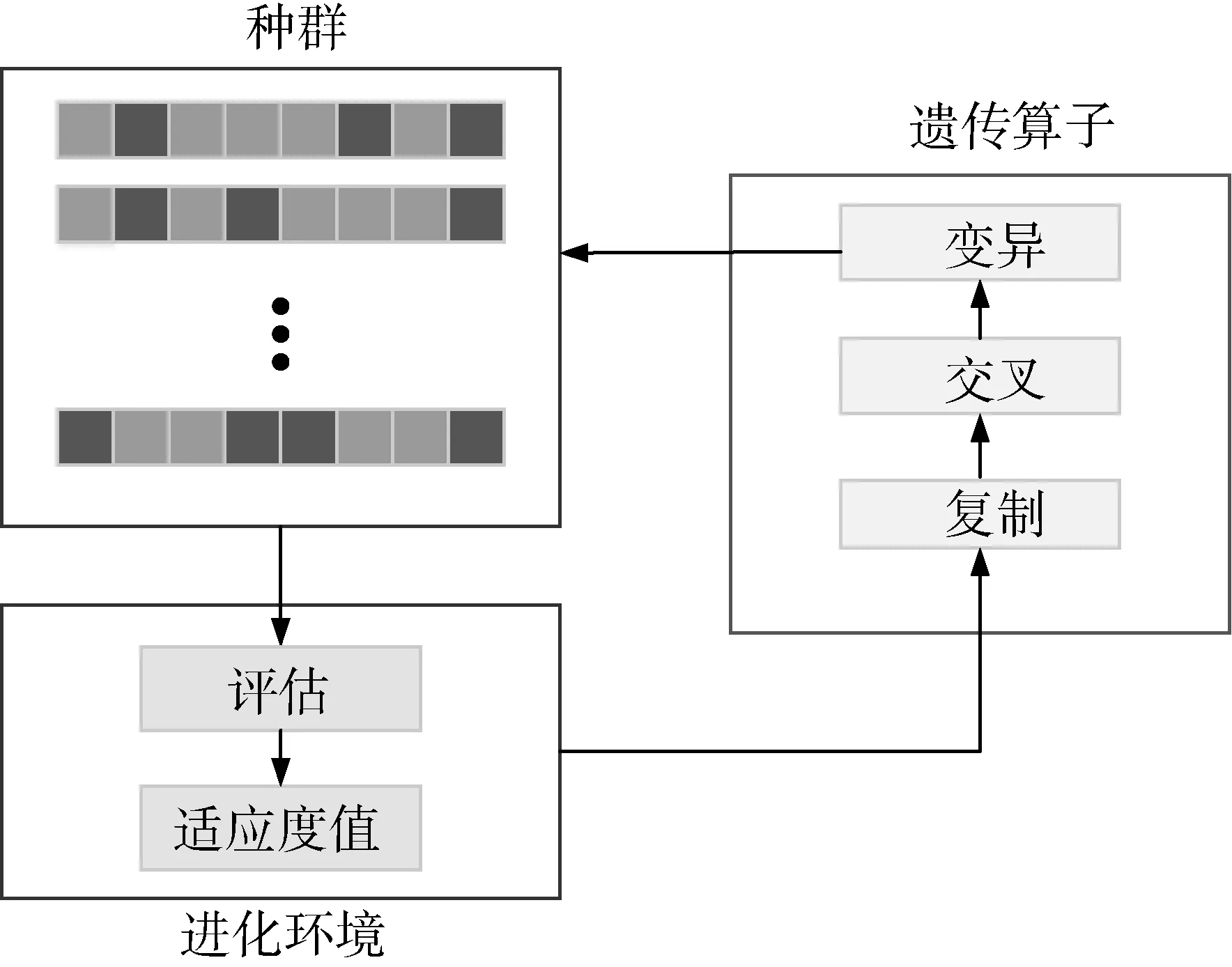
图2 遗传算法进化流程图Fig.2 Genetic algorithm evolution flow

2.2 工具箱使用说明

MATLAB2014a优化工具箱提供了多种优化方法， ga()函数的基本调用格式为：

[x,fval]=ga(fitnessfc,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)[10];

Nvars为自变量数量；A·x≤b为线性不等式约束；Aeq·x=beq为线性等式约束；LB为边界下限值；UB为边界上限值。

2.3 遗传算法实际求解过程

将表1中已知试验油膜轴承参数带入函数编程求解，再根据单目标函数下的最优解求得加权因子分别为：N1=322.6；N2=1 538.5；N3=47 393.4.

(1)编写目标函数程序的M文件[11]simple_fitness.m

function f= simple_fitness (x);

f=6.37*10^(-4)*x(1)*x(3)/x(2)^2+9.545*10^(-3)*x(1)*x(3)/x(2)+846.2*x(2)/x(1)^1.5+0.936/x(1)；

(2)编写最小膜厚作为非线性约束条件的M文件simple_constraint.m

(3)function[g,ceq]=simple_constraint(x)

g=6*10^(-6)-2.282*10^(-4)*x(1)^2*x(2)^(-1)*x(3)*(x(1)+1)^(-1);

ceq=[];

(4)编写主程序：

ObjectiveFc= @simple_fitness；

nvars = 3;

A=[1 0 0;-1 0 0;0 1 0;0 -1 0;0 0 1;0 0 -1];

b=[0.9545;-0.636;0.002;-0.001;0.04;-0.01]；

ConstraintFc = @simple_constraint；

[x,fval]=ga(ObjectiveFc,nvars,A,b,[],[],[],[]，ConstraintFc)；

运行程序，得到结果：x1=0.9545；x2=0.002；x3=0.01.

将现有轴承参数与优化得到的参数带入评判目标函数，分析其对轴承性能的影响，数据如表2所示。

表2 传统设计与优化算法的性能对比
Tab.2 Performance comparison between traditional design and optimization algorithm

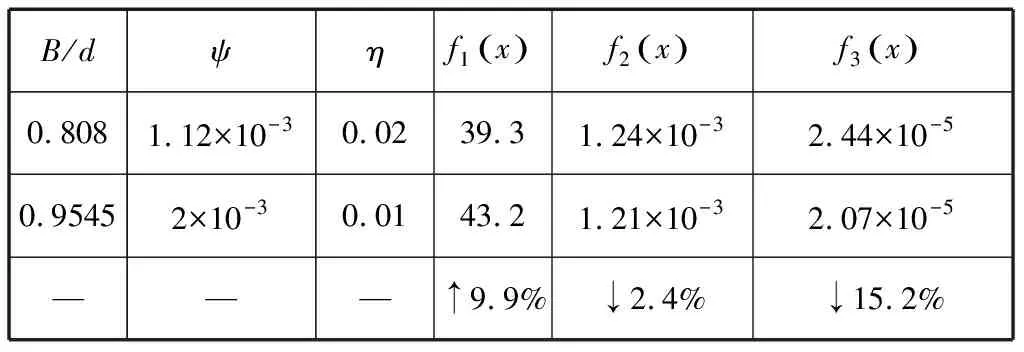
B/dψηf1x()f2x()f3x()0.8081.12×10-30.0239.31.24×10-32.44×10-50.95452×10-30.0143.21.21×10-32.07×10-5———↑9.9%↓2.4%↓15.2%

3 轴承参数对油膜压力的影响

轧机油膜轴承的工作原理是基于流体动压润滑理论[12]，在润滑理论方程中，求解雷诺方程是研究滑动轴承的关键步骤。考虑油膜的静特性时都是稳态的油膜润滑理论[13]，其雷诺方程为：

油膜轴承工作时内部示意图如图2所示，油膜轴承运转过程中形成的极薄油膜会承受承载力，并动态调节轧辊上的轧制载荷。油膜承载力则是通过将轴承衬套上承载区各点的油膜压力进行积分得到[14]。

编写MATLAB程序，得到油膜轴承试验台试验轴承传统设计与优化算法参数下的油膜压力分布，如图4所示。

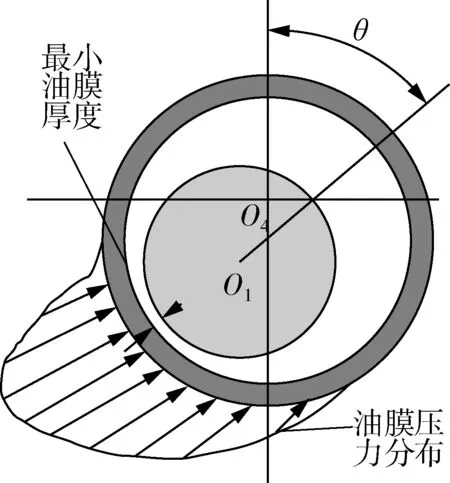
图3 轴承内油膜压力分布

Fig.3 Oil film pressure distribution in bearing

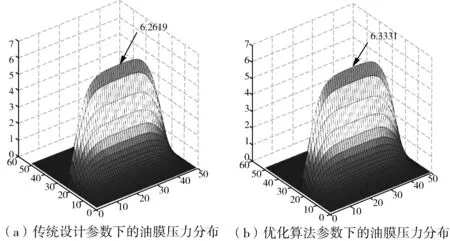
图4 轴承油膜压力分布图

Fig.4 Oil Film Pressure Distribution Diagram of Bearing

4 结论

(1)通过MATLAB遗传优化工具箱对油膜轴承试验台试验轴承进行优化，得到的参数与传统设计参数相比较，在承载能力上提升了9.9%；在摩擦系数上降低了2.4%；在轴承稳定工作的发热量上减少了15.2%.但是遗传算法采用的规则为概率性而不是确定性，所以每次得到的结果存在差异性，可以对比不同算法下得到的优化参数对轴承性能的影响；

(2)利用MATLAB对雷诺方程进行求解，得到传统设计和优化参数下的油膜压力分布图，由图可知增加宽径比有利于轴承承载能力的提高，但是需进一步分析相对间隙对膜厚的影响，并画出轴心轨迹图。