基于无线传感器网络和智能优化压缩感知的山林火灾事件监测

2019-10-23余阳陈钦柱赵海龙韩来君

微型电脑应用 2019年10期

余阳，陈钦柱，赵海龙，韩来君

(1.海南电网有限责任公司电力科学研究院，海口 570311；2.海南省电网理化分析重点实验室，海口 570311 )

0 引言

随着山林绿化面积的不断扩大，森林为人类社会发展提供了宝贵资源[1]。众所周知，火灾是当前威胁森林资源然最主要的因素之一，因此研究有效的山林火灾监测方法具有重要意义[2]。

当前山林火灾监测方法主要围绕遥感卫星技术、地理信息技术和物联网技术[3]三类展开：胡尧结合遥感卫星覆盖性能优势，提出了一种有效山林着火点获取方案[4]；Hou等则利用卫星遥感数据研发了山林火灾动态监测系统[5]，但是由于卫星遥感分辨率低、云层干扰以及监测时间受限等固有缺陷，山林火灾监测实时性和准确性还有待进一步提高。王学祥在分析火灾空间数据的基础上，对山林火灾空间关联性进行了深入研究[6]，然而这类基于地理信息技术的山林火灾监测方法往往需要融合其他两种技术才能得到最好的监测结果。李波等利用无线热传导激光传感网络，提出一种基于物联网的山林火灾监测方法[7]；苏坡则设计了一种基于ZigBee的山林火灾监测系统，有效降低了监测成本，并提高了监测实时性和准确度[8]，但是随着监控数据规模的爆炸式增加，以及监控区域环境的异常复杂性，如何提高无线传感网络(WSN，Wireless sensor network)快速响应和监测有效性已成为物联网技术亟需解决的难题。

WSN作为物联网基础单元，其由大量低成本、具有无线通信和计算能力的传感器节点组成[9]。随着WSN广泛应用，采用WSN进行山林火灾监测具有重要意义。针对山林火灾监控区域内火灾发生数量、发生位置未知以及监控数据规模庞大等特点，提出了一种基于无线传感器网络和智能优化压缩感知的山林火灾事件监测方案，主要做了以下几个方面工作：首先，提出基于WSN的山林火灾监测数学模型，并采用WSN进行火灾报警信息采集。其次，设计基于压缩感知(CS)技术的山林火灾事件分析检测流程，并对CS重构算法进行研究，以完成对稀疏度未知信号的精确重构。最后，在构造稀疏矩阵和测量矩阵的基础上，对提出方案的有效性进行仿真研究。

1 问题描述

设待监控山林为方形区域，并将该区域等分成N个方格，则监控区域内存在N个可能发生火灾的部位。定义向量sN×1=[s1,s2,…,sN]T表示N个可能发生火灾部位监测信号向量(若第i(i∈{1,2,…,N})个方格对应的部位未发生火灾，则其监测信号值si=0)。通常山林火灾发生时只有K个方格内产生火灾信号，因此，当K≪N时，sN×1为K度稀疏向量。此时，采用WSN对山林火灾进行监测，即在山林监测区域内稠密部署大规模传感器节点。

某时刻，WSN利用M个工作节点进行山林火灾监控。当合理设定N的取值，可以认为火灾发生位置即为方格中心，因此根据传感器节点信号测量公式，第j个工作节点的测量值为yj(j∈{1,2,…,M})为式(1)。

(1)

其中dji、hji分别为信号传播距离和瑞丽衰减模型。用向量yM×1=[y1,y2,…,yM]T表示M个节点测量向量，则为式(2)。

(2)

当M≪N时，方程(2)为欠定方程组，因此可以利用压缩感知技术[10]进行求解，进而得到sN×1=[s1,s2,…,sN]T具体表现形式，即实现了对火灾发生部位的准确定位。

2 智能优化压缩感知

CS理论的提出为信号处理领域带来了革命性变革[12]，其认为对于信号xN×1，若存在稀疏矩阵ΨN×N，并且使得xN×1可以用含有K(K≪N)个非零元素的向量sN×1进行，即式(3)。

xN×1=ΨN×NsN×1

(3)

则称sN×1为xN×1在ΨN×N下的稀疏表示，且稀疏度为K。选取一个非相关测量矩阵ΦM×N对xN×1进行投影，则得到测量向量yM×1为式(4)。

(4)

此时公式(2)和公式(4)具有相同的表达形式，CS理论证明，当M≪N时并且AM×N满足RIP条件时[12]，可以通过求解l0范数实现原始信号重构为式(5)。

(5)

观察式(5)可以看出，合理选择稀疏矩阵ΨN×N、测量矩阵ΦM×N以及重构算法，可以精准的实现向量sN×1求解。已经证明l0最小范数求解隶属NP-hard范畴，为了提高稀疏信号重构精度和效率，本文设计改进的离散粒子群优化算法(improved discrete particle swarm optimization，IDPSO)，重新定义粒子编码方式和进化机制，并将IDPSO应用于压缩感知重构算法中，进而得到sN×1的稀疏度K和编码非零位置，最后利用最小二乘法计算幅度信息，从而实现稀疏度未知信号的重构。

2.1 IDPSO算法实现

粒子群优化算法(PSO)是目前应用最为广泛的智能优化算法之一，其将具有相当规模的粒子群随机分布到解空间内，粒子相互之间通过协同进化，最终实现优化问题求解。PSO主要应用于连续优化问题求解，为了能够将PSO与CS重构算法结合，提出改进的离散粒子群优化算法(IDPSO)。

定义1(自我变异更新) 对于粒子Fi，定义自我变异更新操作为随机选择Fi的第m和第n个编码位进行交换，即式(6)。

SVRi(a,b):Fi(Fi1,…,Fia,…,Fib,…,FiN)→

(6)

Fi→Fj:{SVRi(1,2),SVRi(2,3),…,SVRi(U-1,U)}

(7)

其中，U(1≤U≤N-1)表示由Fi转换到Fj需要自我变异更新操作次数。定义{SVRi(1,2),SVRi(2,3),…,SVRi(U-1,U)}为Fi到Fj自我变异更新集合。

定义2(学习进化) 对于粒子Fi，当其学习对象Fj确定后，定义学习进化为式(8)。

Fi,new=Fi+R⊗(Fi→Fj)

(8)

其中，1≤R≤U且为正整数，R⊗(Fi→Fj)表示随机选择Fi到Fj自我变异更新集合中R个自我变异更新操作。

定义3(IDPSO粒子更新策略) IDPSO粒子更新策略定义为式(9)、式(10)。

Fi(t+1)=Fi(t)+R1⊗(Fi→Fbest)+

R2⊗(Fi→Frand)

(9)

Ri=Rmin+(Rmax-Rmin)×

(10)

其中，Fbest、Frand分别为当前种群最优解和随机选取的粒子，f(·)为粒子目标函数值。从定义3可以看出，算法运算初期，Ri具有较大取值，从而使得粒子能够获取更多其他粒子信息，扩展了种群样本多样性；随着进化不断加深，Ri取值不断减少，从而加快了算法收敛速度。

2.2 基于IDPSO的CS重构算法

为了能够将IDPSO应用于CS重构算法中，结合稀疏重构信号向量特点，给出粒子编码和目标函数相关定义。

定义4(粒子编码) 对于N维稀疏度未知信号重构问题，IDPSO粒子Fi(Fi1,…,Fij,…,FiN)编码定义为式(11)。

∀Fij,Fij=1 orFij=0,j∈{1,2,…,N}

(11)

其中Fij、K分别为第j个编码位和信号稀疏度。

定义5(目标函数) 对于IDPSO应用于CS重构算法问题，其目标函数定义为式(12)。

(12)

基于IDPSO的CS重构算法工作流程,如图1所示。

图1 IDPSO优化CS重构算法实现

2.3 山林火灾事件监测实现

采用CS处理WSNs监控数据的关键之一是合理设计稀疏矩阵ΨN×N、测量矩阵ΦM×N，稀疏矩阵与测量矩阵构造实现如下：

对于WSNs网络，当网络工作节点数为M=N时，N个工作节点得到的测量信号向量为式(13)。

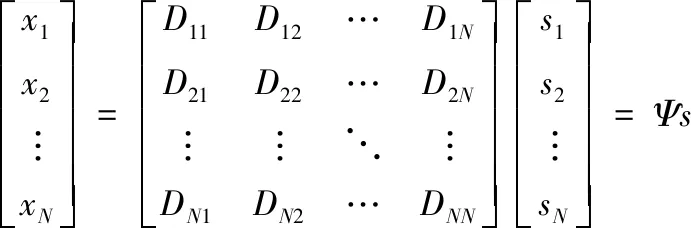
(13)

然而，CS理论认为，当工作节点数M≥O(c(K+1)ln(N/K))时，利用M个工作节点就能够恢复原始信号，即式(14)。

(14)

联立式(13)和(14)有式(15)。

(15)

相关文献已经证明当采用式(13)和式(14)的稀疏矩阵ΨN×N和测量矩阵ΦM×N时，矩阵A能够较好的满足RIP条件[12]，也就是说能够准确的实现稀疏度未知信号sN×1的精确重构。

3 仿真实验

在10 km×10 km山林监测区域内部署2 000个传感器节点，传感器节点性能指标参数和位置信息已知，IDPSO算法相关参数设置如下：种群规模P=300、Tmax=500，Rmax、Rmin根据N的取值大小设定。在进行模拟实验时，人为的在不同区域制造火灾信号，以对实验结果进行分析，评价指标为平均相对误差σre和检测成功率Pc为式(16)、式(17)。

(16)

(17)

其中D、σi分别为实验次数和第i次试验误差，θ为监测成功阀值。

3.1 参数设置实验

在对山林监测区域进行网格划分时，N的取值大小对火灾监测精度和CS重构算法运算时间具有重要影响，不同N设定下火灾监测成功率和CS重构算法运算时间变化曲线图,如图2所示。

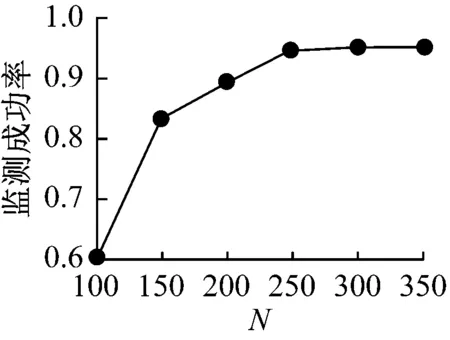
a 监测成功率曲线图

b CS重构算法运算时间曲线图

从图2可以看出，随着N的取值不断增加，火灾监测成功率不断升高，而CS重构算法运算时间也不断增加，特别的当N≥250时，监测成功率都在95%以上，并且基本保持稳定，但是CS重构算法的运算时间迅速提升，因此，在保证较高监测成功率的前提下，N的取值越小越好。

为分析参数M对监测性能的影响，分别选本文算法、文献[13]和GMP重构算法进行对比实验，每种检测方案重复实验D=50次。M不同取值时，3种重构算法下火灾监测成功率对比结果(此时设定信号稀疏度K未知),如图3所示。

图3 不同M取值3种算法监测成功率对比

从图3可以看出，当信号稀疏度K未知时，随着M不断增加，本文监测成功率不断升高，特别的，当M≥100时，监测成功率达到了98%以上，而GMP和文献[14]监测都在80%以下，而且波动较大，可见本文算法能够完成稀疏度未知信号的精确重构，这也符合山林火灾监测特点，因为我们事先并不知道有多少个区域发生火灾。