小学数学课堂应当成为提高学习力的主阵地

2019-10-23赵丽芸

名师在线 2019年28期

关键词：棱长涂色内角

赵丽芸

（江苏省南京市栖霞区实验小学，江苏南京 210046）

引言

当前的基础教育课程改革的热点之一是提高学生的核心素养，而学会学习是学生应具备的核心素养之一。因此，如何让数学课堂真正成为提升学生学习力的主阵地，让学生的学习力在有限的课堂教学时间内得到锻炼和提升，是小学数学教师应探索和研究的一个重要问题。

一、把握好个体与主体的关系

在当前的课堂教学中，教师越来越注重维护学生的主体地位，创设了足够的空间和时间来培养学生的学习力，设计了诸多体现学生主动“学”的活动。但是，教师往往只关注学生群体，而不能关注每一个个体，学生主体地位只是体现出“有学生”参与了学习活动，而忽视了学生的个体[1]。比如，某位教师教学《多边形的内角和》时，学生通过小组合作探究用“把四边形分成两个三角形”的方法，得到四边形的内角和为两个三角形的内角之和，即180°×2=360°；之后，教师希望学生通过刚才的方法，将知识迁移，在探究五边形的内角和时能将五边形分成3个三角形，得到五边形的内角和为3个三角形内角之和，即180°×3=540°，以此类推，得到六边形、七边形……n边形的内角和为（n-2）个三角形内角之和，即180°×(n-2)。

以表面上看，该教师确实做到了尊重学生的主体地位，设计了小组合作、自主探究等学习活动，探究的方法也是学生自己迁移、自己想到的，并在学习过程中让学生自主表达自己的探究过程和探究方法。

但是在热热闹闹的学习活动中，学生甲是这样做的：将五边形分成一个三角形和一个四边形，那五边形的内角和就是三角形的内角和加上四边形的内角和，即180°+360°=540°；这位教师看了学生甲的方法后，问其他学生：“这个方法可以吗？”学生回答：“可以。”之后没有对学生甲的方法再做评价，而是直接出示了表1，由于有了前面的铺垫，所有学生都填得正确无误。

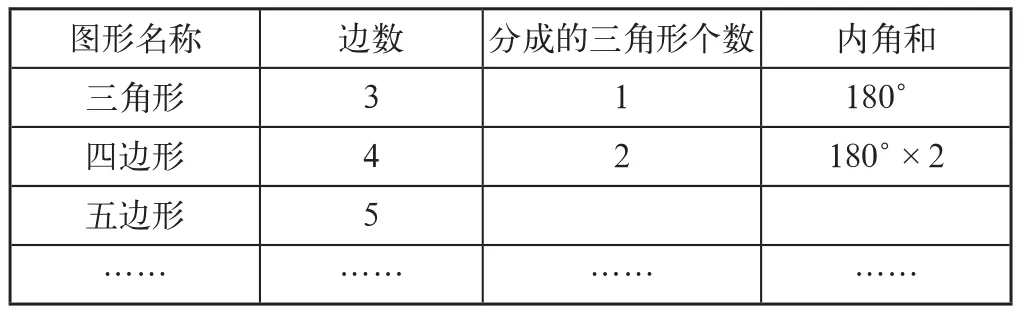
表1

这样的课堂看似热闹灵活、开放自由，实则缺乏主体本质上的灵动。要培养学生的学习力，就要尊重每个学生的主体地位，学生个体即学习主体，并不是大部分学生才是主体。从这个意义上来说，学生甲的方法虽不是教师所倡导的主流方法，但非主流方法同样是学习主体中个体的主流方法，同样需要教师关注。鉴于个体即主体，本环节的学习可以再开放一点：探究出四边形的内角和表达式后，暂时不出示表1，而是以认领的形式让学生自己选择一个多边形来研究其内角和。这样做的好处就是让学生的思维不受约束，他们不再拘泥于“将多边形分成若干个三角形”这种思考方法，而是有更宽广的思维空间。或者，教师在肯定了学生甲的方案后，引导全体学生思考这一方法可不可再变化，进而让学生发现在这一方法的基础上，还可以把其中的四边形再分成两个三角形，然后学生分别汇报，类推到任意的n边形的情况，再由学生汇总概括出示表1。最后，教师引导学生观察表1的纵向内容，让学生总结“将多边形分成若干个三角形”的思考方法，从而获得180°×(n-2)的表达式。

教师在教学中要把握好主体和个体的关系，尊重每个个体的主体地位，使学生通过展示交流想法和意见，经历探究过程自我生长出正确认知，这样才能从根本上提高学生的学习力。

二、把握好铺垫多与少的关系

有的教师认为培养学生的学习力，就应该在教学中给学生多一些自由，提示越少越好。实则不然，提示的多少因教学内容的不同而不同，有时需要教师提供较多的铺垫来帮助学生找到思路，有时只需两三句点拨，学生就能自主思考。例如，在教学《表面涂色的正方体》时，笔者先让学生观察棱长为2或3厘米的正方体表面涂色后，把它切割成棱长为1厘米的小正方体，其中三面涂色、两面涂色、一面涂色的小正方体个数分别是多少，然后让学生独立探究切割棱长是4厘米、5厘米的正方体，得到三面涂色、两面涂色、一面涂色的小正方体个数分别是多少，最后让学生根据三面涂色、两面涂色、一面涂色小正方体的位置特点，比较表2中数据的特点，发现规律，并让学生通过切割棱长为6厘米、7厘米的正方体来验证发现的规律，从而得到当棱长为n（n＞2）时，三面涂色、两面涂色、一面涂色的小正方体个数分别是8，(n-2)×12，(n-2)2×6。

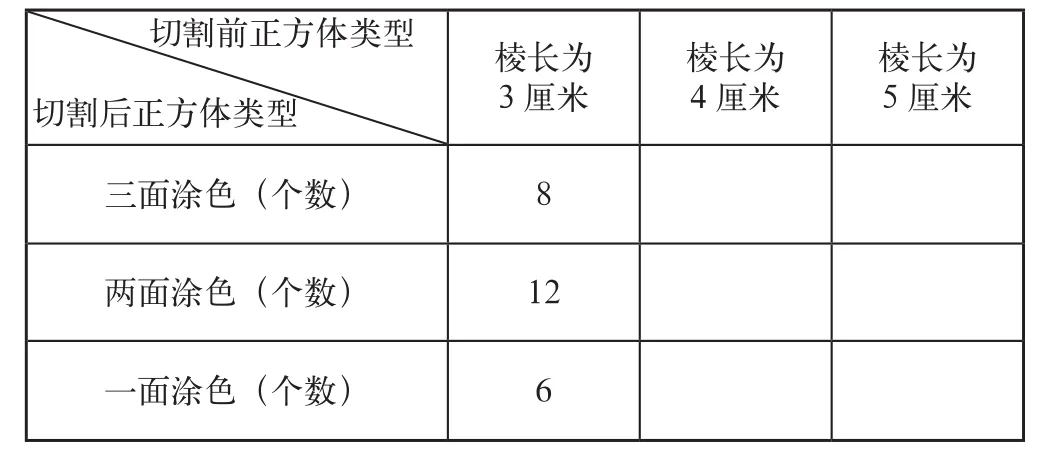
表2

像此类探究规律的综合实践活动，特别是探究比较抽象的规律时，教师需要安排足够的思维铺垫，才能使学生慢慢地接近规律的本质，如果没有棱长为2厘米、3厘米、4厘米、5厘米情况时的探究和讨论，学生无法得到三面涂色、两面涂色、一面涂色小正方体的位置及数据的特点。那么，当棱长为n时，探究三种涂色小正方体的个数就是一句空话。

培养学生的学习力，不以铺垫思维出现的多少论成败。如果学生在学习中无所适从，铺垫思维环节过少，学生的思维就会被束缚，缺乏造成认知冲突的机会，也就无法提升他们的思辨能力。因此，按照内容的难易和学生的学情，决定铺垫思维环节的多少，才能够有效提升学生的思维力和学习力[2]。

三、把握好引导与思辨的关系

培养学生的学习力，教师要把握好引导和思辨的关系，减少一些不必要的引导，给学生多留一些思辨的机会，让他们学会自己解决问题。例如，笔者在执教《除数是小数的除法》的算法探究时，学生已经掌握了除数是整数的小数除法的计算方法，而且在前面探究平行四边形面积等教学中，也应用了“转化”的思想方法，有了这些知识经验基础，学生经过自己的尝试探究，是能够自己推导得到算法的，而这个过程又恰恰是计算教学的教育价值所在。因此，利用好、实施好这个过程，就是学生自主迁移的过程。其中，学生学会在自己的头脑中检索、整合、构建、加工已有的知识经验，从而解决新的问题，就是自身学习力的提升。