卡尔曼滤波器在移动机器人定位中的应用

(华北科技学院电子信息工程学院 河北 廊坊 065201)

引言

1960年,卡尔曼发表了用递归方法解决离散数据线性滤波问题的论文(A New Approach to Linear Filtering and Prediction Problems)[1]。卡尔曼滤波应用广泛且功能强大,它可以估计信号的过去和当前状态,甚至能估计将来的状态,即使并不知道模型的确切性质[1]。

卡尔曼滤波器又称为最佳线性滤波器[2]，它的好处有很多，比如：简单易实现、又是一个纯时域的滤波器，不需要进行频域变换。卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法[3]。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

一、卡尔曼滤波的原理

(一)预测

假设移动机器人正在运动，用它的位置和速度来表示它当前的状态，t时刻的位置为pt，速度为vt，加速度为ut，那么在t时刻移动机器人的状态向量可以用一个二维的列向量xt=[pt,vt]T表示。假设移动机器人的加速度量由外部控制量(油门加速或控制命令)得到[4]，如果已知上一时刻的状态xt-1可推出其在t时刻的速度与位置如下:

移动机器人的速度：vt=vt-1+ut×Δt

其中Δt是两个时刻的时间间隔，观察上公式可知输出变量都只是输入变量的线性组合，这就是卡尔曼滤波器是最佳的线性滤波器原因，因为它只能描述状态与状态之间的线性关系，既然是线性关系，则可改写成矩阵的形式如下：

vt=0×pt-1+1×vt-1+ut×Δt

把两个状态变换矩阵提取出来，公式可以简化成如下：

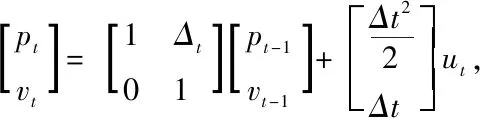
由状态转移矩阵Ft和控制矩阵Bt表示的移动机器人的状态转移公式为：

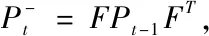
(二)更新

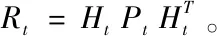
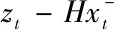
卡尔曼系数Kt作用主要有两方面，一是权衡预测状态协方差P和观测的协方差矩阵R的大小来决定预测模型更可靠，还是相信观察模型更可靠，若预测模型更可靠，则残杀的权重就会小一点，若观察模型更可靠，则残差的权重就会大一点。第二个作用是把残差的表现形式从观察域转换到状态域[8]。

最后一步是更新最佳估计值的噪声分布，即噪声协方差矩阵的更新，用公式表示为：

二、卡尔曼滤波器的系统模型

综上所述，我们已经得到了卡尔曼滤波器中的五个公式，在这五个公式中前两个公式是通过上一时刻的状态来预测当前时刻的状态，这表示这并不是最佳的估计值。再把当前时刻的观测值考虑进去即为更新，经过更新后的值就是最佳的观测值。

预测：

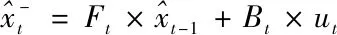
更新：

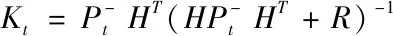
三、结束语

由于卡尔曼滤波在机器人SLAM中主要用于位置估计，所谓的估计值是估计位置坐标，输入传感器数据包括码盘估计的位置，陀螺仪的角速度等。采用卡尔曼滤波的方法来实现移动机器人位置的估计，利用卡尔曼滤波的良好的跟踪性能，它可以根据当前的观测量和之前的观测数据，根据线下那个最小方差原理，求出最优估计。采用递归方法解决线性滤波问题，只需要当前的测量值和前一个采样周期的估计值就能够进行状态估计，不需要大量的存储空间，每一步的计算量小，计算步骤清晰，非常适合计算机处理。最终输出的最佳估计值用作机器人的当前位置，其由除导航算法之外的其他程序调用。