平原水库大坝涵洞地基承载力研究

杜九博，牟燕妮，高 峰，李玉莹

(山东省水利勘测设计院，山东 济南 250013)

1 概述

平原水库一般位于大江、大河下游冲积平原地区，这类地区地质岩性多数为黏土、粉质黏土、粉土、砂土、砂壤土、粉细砂等组成。平原水库的出入库功能需通过埋置于坝体内的涵洞来实现。涵洞工程地基承载力的确定不仅影响大坝的安全，而且影响工程的投资和施工工期，其分析计算历来是平原水库设计的重点和难点。

水利工程涵洞设计没有相应的规范或规程，设计人员需要从相关规范和手册中寻找依据。SL 744—2016《水工建筑物荷载设计规范》对涵洞的土压力进行了规定。《水工设计手册》(第2版)对涵洞的结构计算提供了依据，而目前各参考资料很少涉及涵洞下地基承载力的计算。目前，设计人员多依据熊启钧编著的《涵洞》一书提供的地基承载力验算方法进行设计，该书采用JTG D63—2007《公路桥涵地基与基础设计规范》进行地基承载力验算；也有设计人员按照GB 50007—2011《建筑地基基础设计规范》进行地基承载力验算。使用以上方法进行水工涵洞地基基础设计时均存在规范不适用的情况，设计人员也有使用上的疑惑。本文对涵洞承载力计算中存在的问题进行分析，运用GTS NX三维有限元软件，分析涵洞对大坝安全的影响，提出解决涵洞下地基承载力问题的新思路。

2 问题和疑惑

2.1 应用《公路桥涵地基与基础设计规范》的问题

按照JTG D63—2007，修正后的地基承载力容许值计算如下：

[fa]=[fa0]+k1γ1(b-2)+k2γ2(h-3)

(1)

式中，[fa]—修正后的地基承载力容许值，kPa；[fa0]—地基承载力基本容许值，kPa；k1、k2—基底宽度、深度修正系数；γ1—基底持力层土的天然重度，kN/m3；γ2—基底以上土层的加权平均重度，kN/m3；b—基础底面的最小边宽，m；h—基底埋置深度，m。

式(1)中第三项为地基承载力的深度修正，在《涵洞》书中提供的计算例题，h取得是涵洞底高程至大坝填土顶高程的总高度，如图1所示，因而在平原水库涵洞中仅深度修正提高的承载力占到修正后容许承载力的40%左右。实际工作中，大部分设计人员也是按此方法进行计算。

图1 基底埋置深度

公式(1)中的承载力深度、宽度修正是根据浅基础剪切破坏的原理推导出来的，有一定的适用范围，在规范的条文说明中也有解释。当基础四周有填土，且填土的超载作用能够对基础四周的土体可能出现的隆起破坏起到限制作用时，基底埋置深度才可以从填土顶面起算；仅有一侧填土，则仍应自原地面起算；其他情况应具体分析，按不利情况考虑。由此可以看出，深度修正采用的埋置深度取用地基剪切破坏圆弧滑动面范围内填土高度的最小值才符合规范的要求，才是偏于安全的做法，如图2所示。所以，在涵洞地基承载力计算时直接套用桥涵地基规范是不合适的。

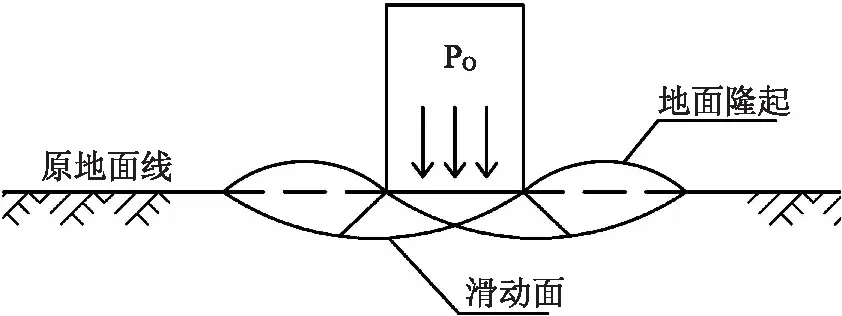
图2 地基整体剪切破坏

2.2 应用《建筑地基基础设计规范》的问题

按照GB 50007—2011，修正后的地基承载力特征值计算如下：

fa=fak+ηbγ(b-3)+ηdγm(d-0.5)

(2)

式中，fa—修正后的地基承载力特征值，kPa；fak—地基承载力特征值，kPa；ηb、ηd—基础宽度和埋置深度的地基承载力修正系数；γ—基础底面以下土的重度，kN/m3；γm—基础底面以上土的加权平均重度，kN/m3；b—基础底面宽度，m；d—基础埋置深度，m。

式(2)中第三项为地基承载力的深度修正。该公式的推导原理与桥涵地基规范类似，当基础四周有填土，且填土的超载作用能够对基础四周的土体可能出现的隆起破坏起到限制作用时，基底埋置深度才可以计入填土高度，且填土的计入高度取基础四周超载宽度大于基础宽度的2倍范围内的最小值。由此可见，涵洞地基承载力设计时简单套用上述公式，按照大坝最大填土高度计算地基承载力特征值是不安全的。

2.3 地基承载力计算与工程实践的疑惑

涵洞是埋置于坝体中的构筑物，可以看作是坝体的一部分。在涵洞自身不发生强度破坏和变形破坏的情况下，涵洞的变形与其四周的坝体基本是一致的；而且涵洞是空心结构，一般情况下，与不埋置涵洞的位置相比，涵洞下的地基压力可能是减小的(局部也可能增加)，因此，不可能出现涵洞下地基土单独出现沉降破坏的情况。从常识上判别，涵洞作为一个埋置于坝体的结构构件，对坝体的安全应该有增强作用。因此，设计人员常常有这样的疑惑：如果不埋置涵洞，坝体是满足安全要求的，为何埋置涵洞后，地基承载力反而不满足安全要求？

由于对坝体破坏原理上的认识不足，实际工程中，也常常会出现为了满足承载力的要求，加大涵洞基础的宽度和刚度，或者进行地基处理的情况，不仅增加了工程投资，而且大大延长了工程工期。

3 工程实例

3.1 工程主要尺寸

以南水北调东线一期工程阳谷县续建配套工程陈集水库出库涵洞为例进行分析，涵洞纵断面图如图3所示。

图3 涵洞纵断面图

3.2 计算参数

主要材料参数见表1。

表1 主要材料参数

3.3 计算模型

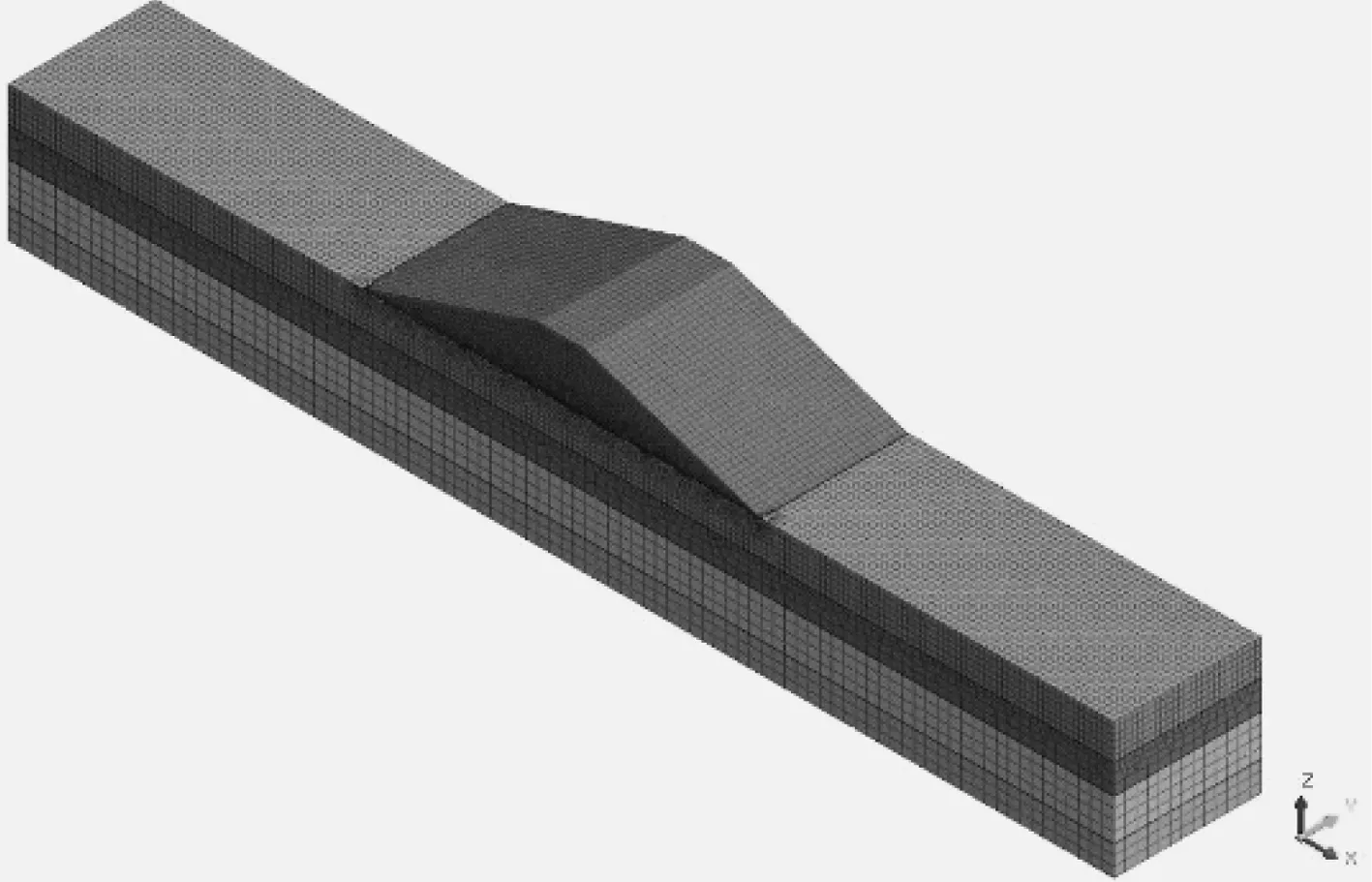
图4 大坝模型(模型一)

采用GTS NX软件进行分析计算。计算模型顺大坝轴线方向长度取50m，网格划分全部采用三维实体单元，采用混合网格生成器，尽量多生成六面体单元，单元划分控制尺寸0.25～2m。为了便于对比分析，将不设置涵洞的大坝模型称为模型一，如图4所示；将设置涵洞的大坝模型称为模型二，如图5所示(图中以涵洞中轴线为对称轴，显示一半模型)，涵洞内净高、净宽尺寸均为2m，壁厚0.5m。

图5 设置涵洞的大坝模型(模型二)

4 计算结果

4.1 沉降分析

模型一的整体沉降云图如图6所示，模型二的整体沉降云图如图7所示。比较两模型的计算结果可知，设置涵洞后，大坝的整体沉降计算结果基本不变。

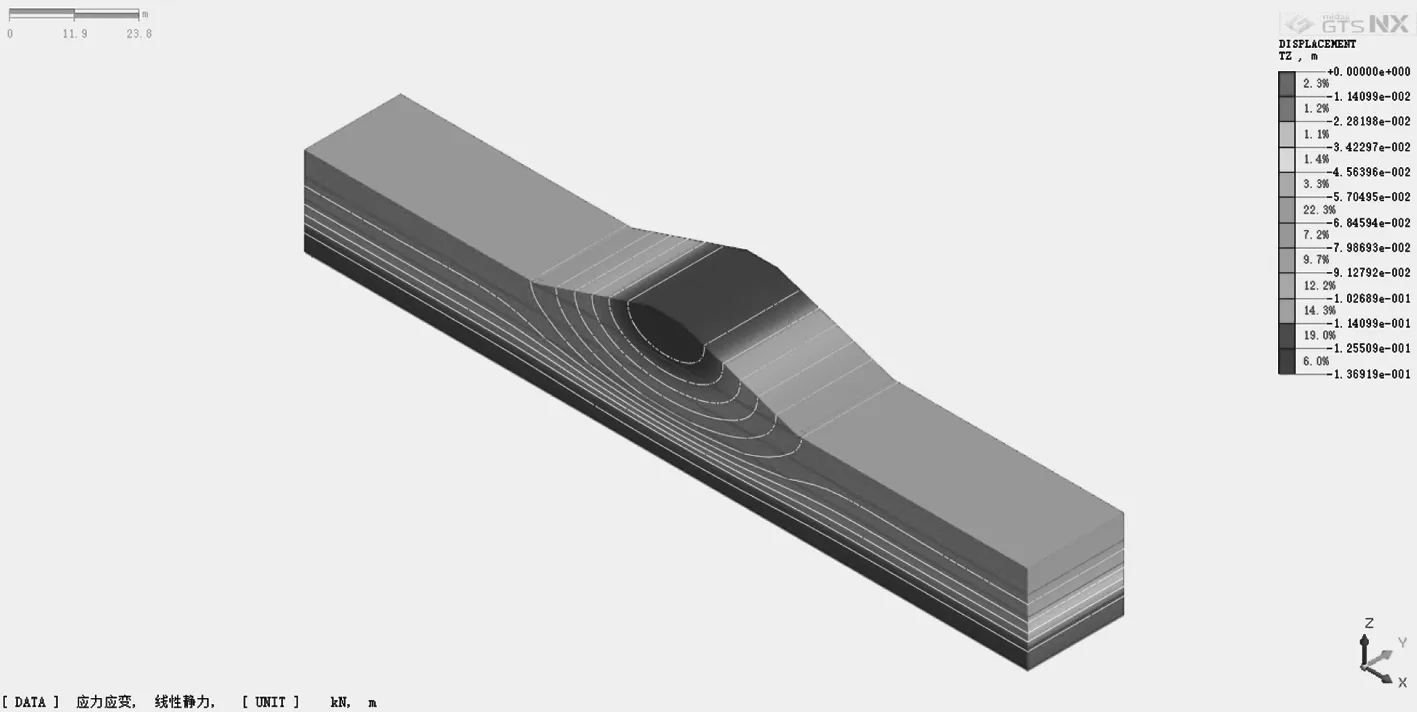
图6 整体沉降云图(模型一)

图7 整体沉降云图(模型二)

单独取涵洞下第一层土体的上表面单元作为研究对象，判断涵洞对其下地基沉降造成的影响。模型一的局部沉降云图如图8所示，模型二的局部沉降云图如图9所示。比较两模型的计算结果可知，设置涵洞后，大坝的局部沉降计算结果也基本不变。

图8 局部沉降云图(模型一)

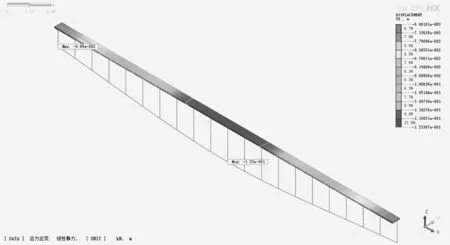
图9 局部沉降云图(模型二)

综上沉降分析可以看出，涵洞作为嵌入大坝中的局部构件，其变形与周围大坝的变形是一致的，对大坝沉降的影响可以忽略不计。

4.2 稳定分析

采用基于强度折减法的Midas GTS有限元计算软件进行边坡稳定计算。

强度折减法计算采用严格的理想弹塑性数值解法，在数值计算过程中，通过逐步减小料强度(按同一比例降低岩土粘聚力和内摩擦角)，直到某一点计算不收敛为止，即认为该点处于破坏状态，最大强度折减率即为最小安全系数。其数学模型如下：

(3)

式中，FS—边坡稳定安全系数；τ—边坡材料的剪切强度；τf—滑动面的抗剪应力；SRF—强度折减系数。

该方法是一种类似于真实情况的方法，可以满足平衡力条件、变形协调条件、本构方程和边界条件等方程，可以较为真实地模拟边坡破坏的形态及更好地体现现场条件，得到边坡的最小安全系数及边坡破坏性状的详细信息。

模型一的塑性应变云图如图10所示，稳定计算安全系数是1.9546；模型二的塑性应变云图如图11(无涵洞侧)、图12(有涵洞侧)所示，稳定计算安全系数是2.1461。比较两模型稳定计算结果，模型一的破坏滑动面出现在贯通的塑性应变滑弧上，模型二的破坏滑动面出现在与涵洞接触的坝体局部。因此，设置涵洞对大坝的稳定安全系数是提高的。上述计算采用的是施工完建期荷载；采用其他工况进行计算，也能得到相同结论，不再累述。

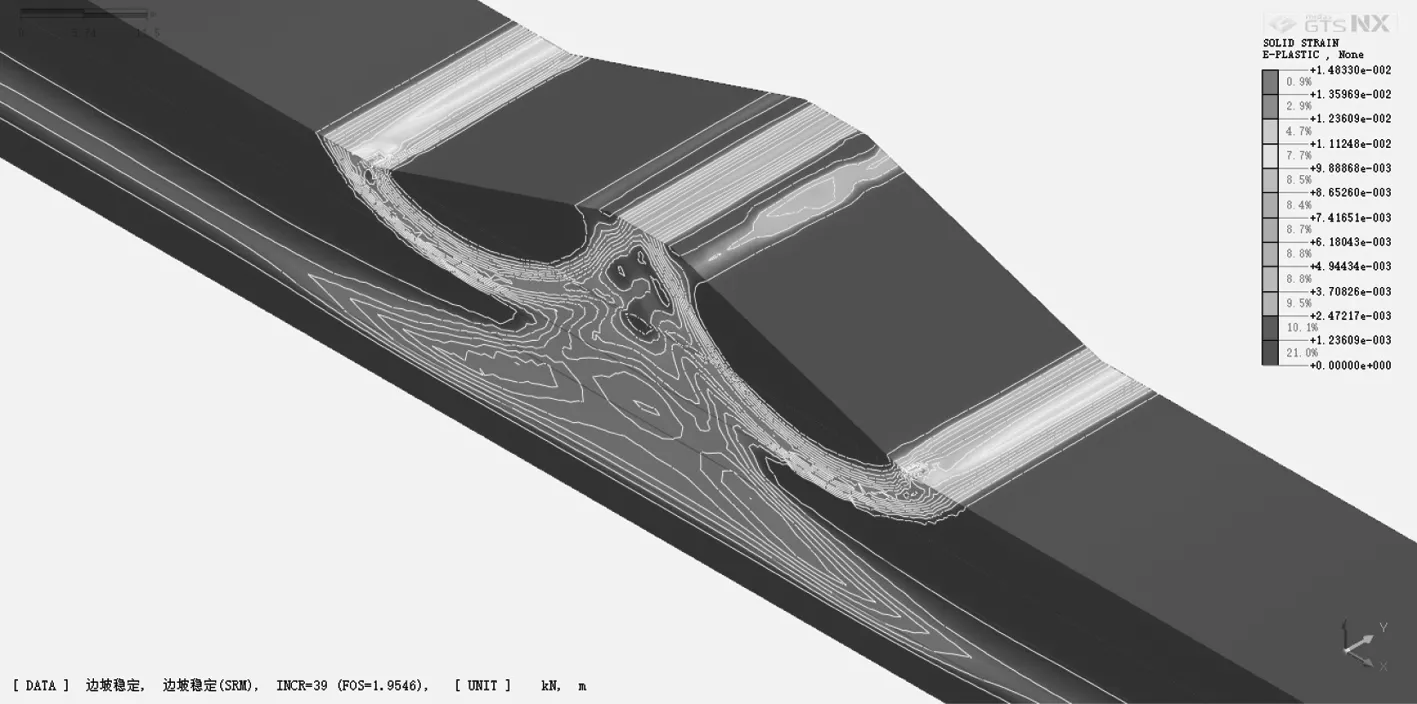
图10 塑性应变云图(模型一)

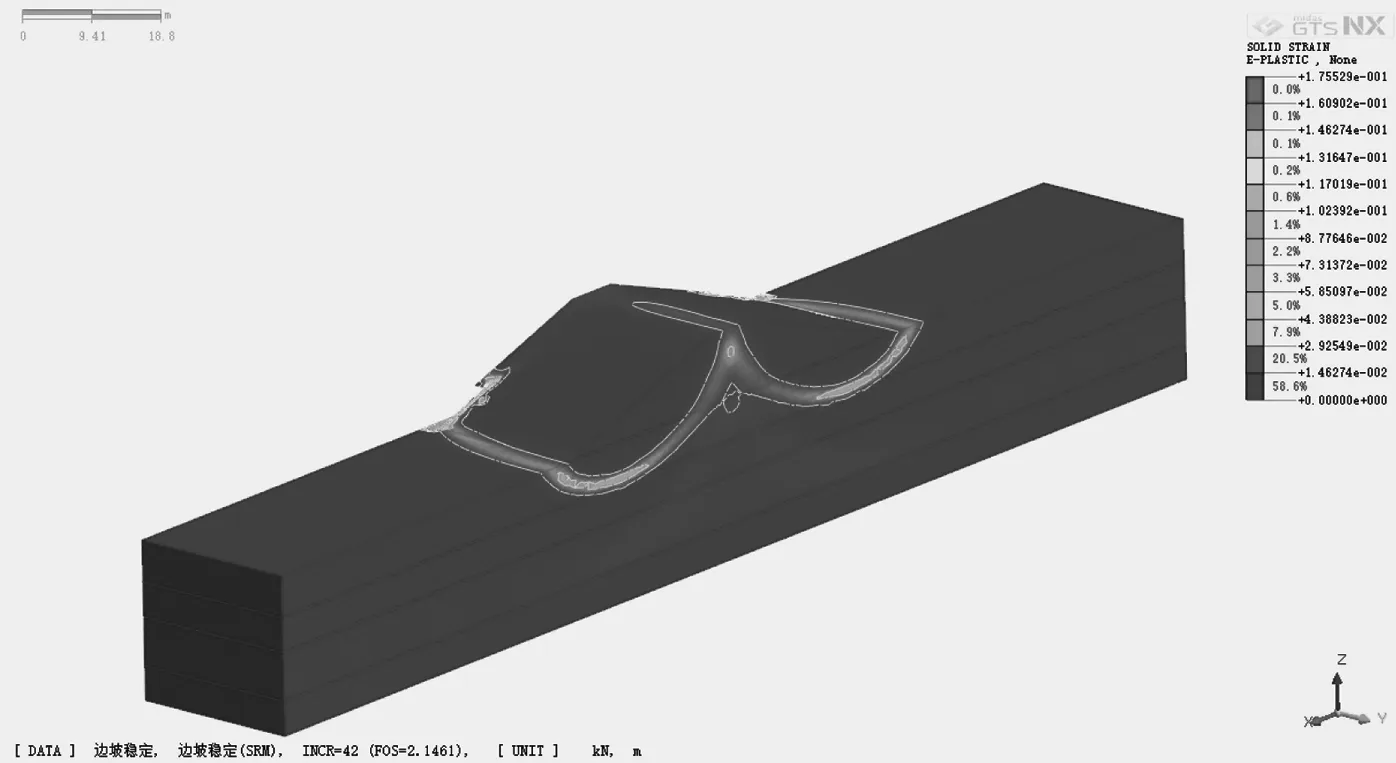
图11 塑性应变云图(模型二无涵洞侧)

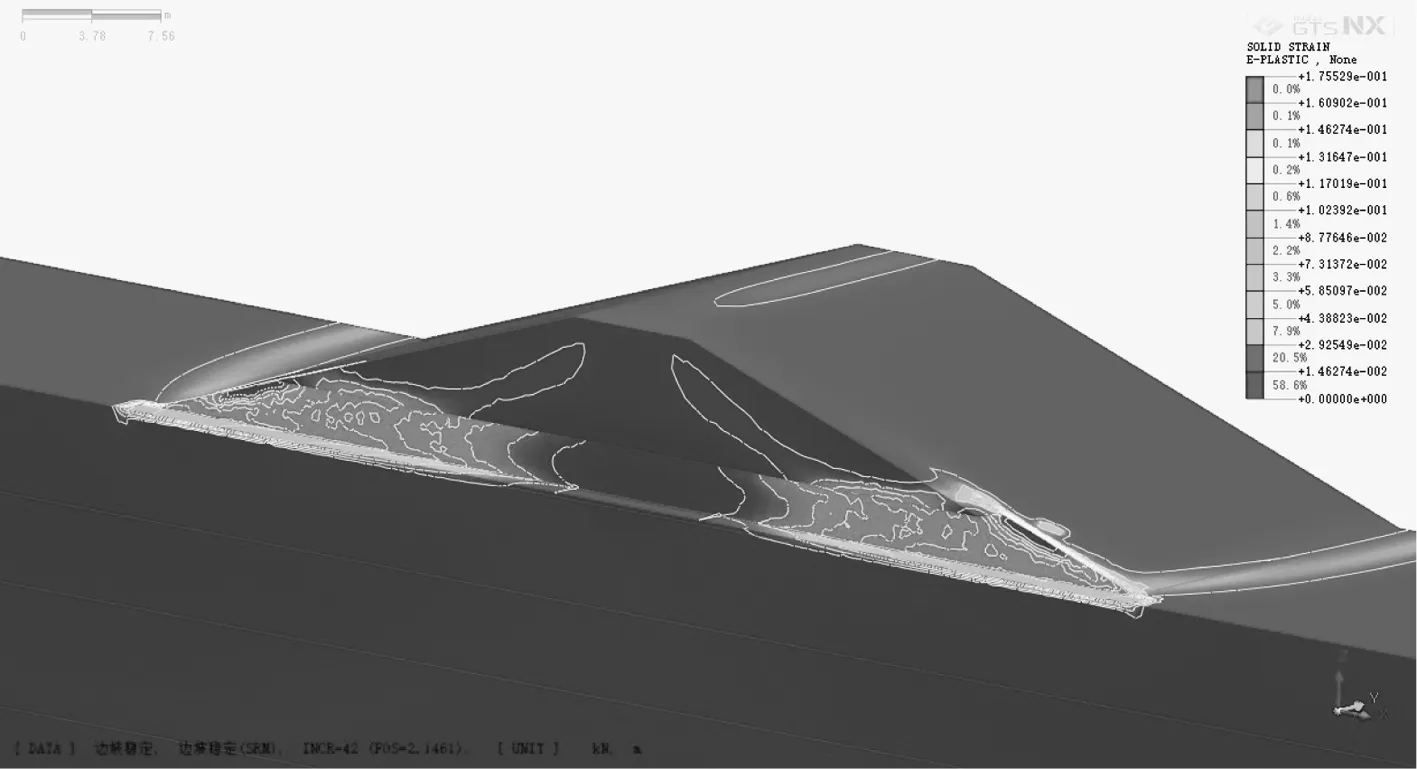
图12 塑性应变云图(模型二有涵洞侧)

综上沉降分析和稳定分析可知，在涵洞自身结构安全情况下，涵洞不会对坝体的安全造成不利影响。

5 结语

本文分析了现有平原水库大坝涵洞地基承载力计算中存在的问题，以实际工程为例，分析了涵洞对大坝的沉降计算和稳定分析的影响，对同类工程设计提出建议：无论是地基的承载力分析，还是大坝的边坡稳定分析，本质都是土体中的剪应力不大于抗剪强度，寻求满足安全条件下的最不利塑性开展区，可以说是一个问题的两种表现形式，分别适用于不同的建筑物；涵洞作为内置于坝体中的一个构件，对地基造成的破坏不会先于大坝的整体稳定破坏。因此，在涵洞自身结构安全和大坝稳定满足规范要求的情况下，不必再验算涵洞下的地基承载力。