混凝土埋石重力坝深层抗滑有限元模拟研究

刘建祖，余启飞

(1.江西省宜春市袁州区水务局，江西 宜春 336000； 2.江西水利职业学院，南昌 330013)

0 引 言

本文参考案例混凝土埋石重力坝工程实用技术数据，借助ANSYS专业智能工程有限元模拟系统，重点围绕溢流段坝体深层稳定抗滑性态，对混凝土埋石重力坝深层抗滑专题开展有限元模拟分析研究，以期为同类工程应用提供研究和技术参考，助力建筑安全稳固的混凝土埋石重力坝工程。

1 案例工程简介

大滩口水库是以防洪灌溉为主、兼顾发电和城乡供水的Ⅲ等中型水利枢纽工程，位处我国江南。设计洪水位618.48 m，核校洪水位620.73 m，常规蓄水位620.00 m，总库容6 850×104m3，控制流域面积1 330 km2。工程由坝体、泄洪建筑物、引水建筑物等组合构成。坝体为C15重力埋石混凝土坝，顶高622.0 m，最大高程59 m，坝顶宽7 m，长190.0 m。从右到左逆坝轴线依次为右岸非溢流段、厂房坝段、溢流段和左岸非溢流段。溢流前缘净宽度50 m，堰顶高度608.0 m，溢流段长度74 m。枢纽临时建筑5级，次要建筑4级，永久性建筑3级。

坝址揭露为侏罗系上统(293sJ～13sJ)遂宁组地层，由黏土岩、细砂岩、岩屑长石砂岩和粉砂岩构成。上游侧岩层略倾偏右岸，倾角在5～9°之间。弱风化风化址基岩层厚度多在2～5 m之间，最大厚度8.4 m左右。强风化址基岩层厚度多在1～2 m之间，最大厚度4.5 m左右。

坝基砂岩Ⅱ-Ⅱ′勘测线蚀余河床厚度在8.18～10.65 m之间，Ⅲ3-2夹层存在局部的泥化状态。Ⅲ-Ⅲ′勘测线下游构成跌坎，存有临空面，有裂缝顺河向发育，稳定抗滑非常不利。基岩体有弱软夹层存在。

2 有限元数理模型的创建

2.1 范围及约束条件

模型范围包括坝身及深浅坝基。系统建模型时，如果坝基范围宽度不够，会使运算结果发生较大偏差；而如果在精度提高不大的条件下，过大的取值范围又会带来过度耗时及浪费资源的问题。经系统筹划，本研究计算范围为坝基取深80 m，自坝址下向取75 m，自坝踵上向侧取65 m。

底边取固定约束，上下侧取法向约束，坐标为：坝轴线下游向为X坐标正方向，垂直上向为Y轴正方向，以沿坝轴线取为Z轴正方向。

计算截面及有限元模型具体见图1和图2。

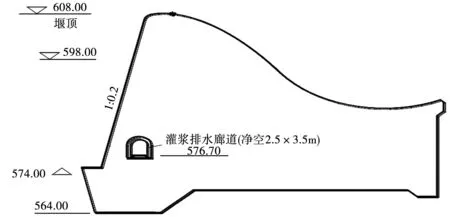
图1 溢流段截面图

图2 溢流段有限元网络图

2.2 模型及基本材料参数

本文重点探究溢流段的稳定抗滑问题，仅以溢流段为分析对象。由坝身和深浅坝基三部分创建溢流段重力坝稳定抗滑性模型，运用ANSYS专业有限元水工模拟系统，对溢流段开展建模，见图2。

坝身以ANSYS专业混凝土单元给与离散创建，节点1 468个，总单元987个。

坝基以solidl85实体三维单元给与离散创建，深坝基节点13 968个，总单元10 080个；浅坝基节点2 616个，总单元1 635个。坝体稳定性有限元分析节点17 508个，单元12 702个。选用D-P弹塑屈服准则。模型参数依据案例工程应用参数，并结合模型实际情况确定，主要材料参数具体见表1和表2。

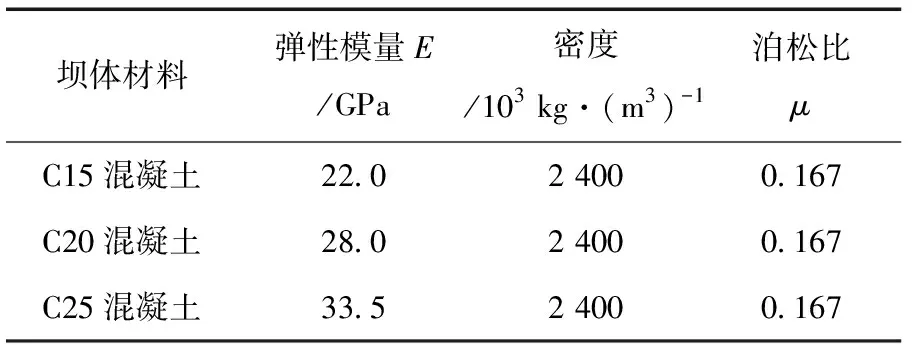
表1 坝身材料参数

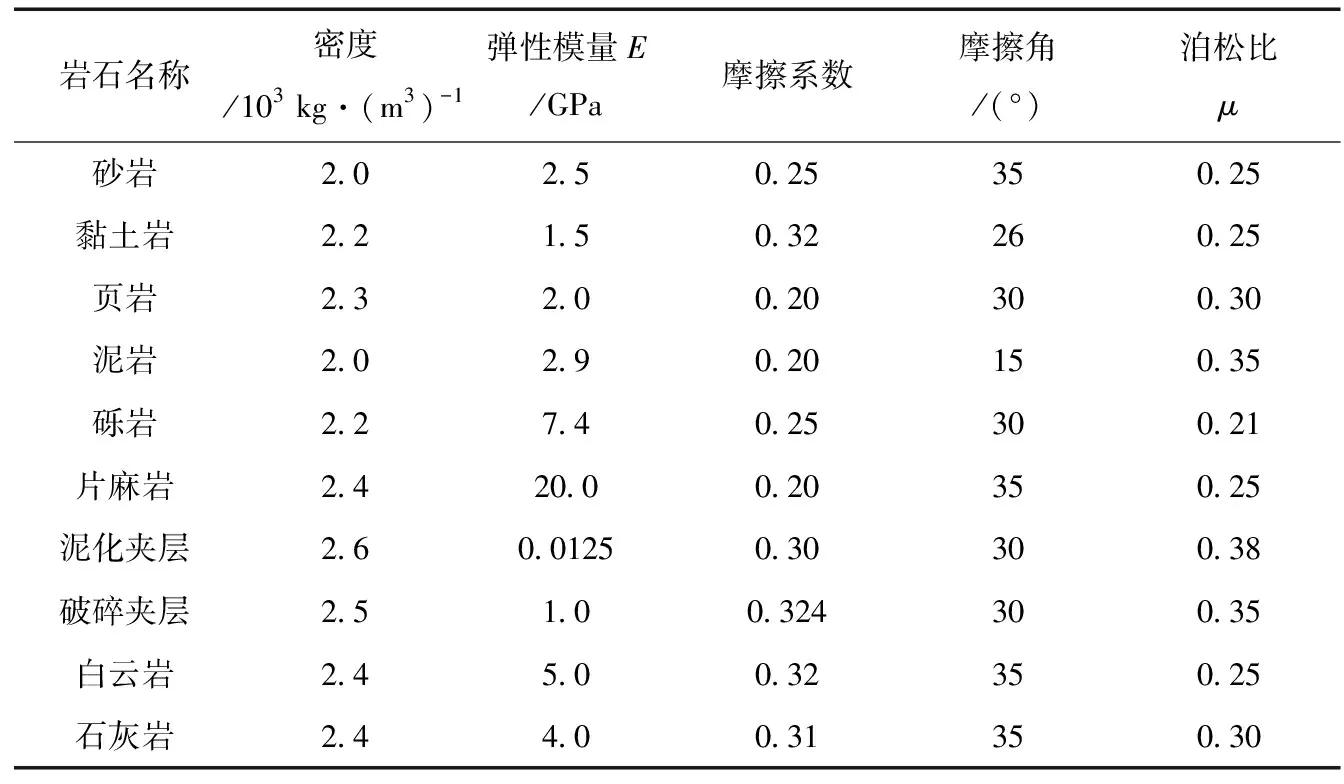
表2 基岩设计力学参数表

2.3 计算工况

模拟工况选用核校洪水位、设计洪水位、一般高水位3种工况。

核校洪水位：下游586.99 m，上游620.73 m

设计洪水位：下游584.40 m，上游618.48 m

一般高水位：下游576.00 m，上游620.00 m

模拟载荷包括坝体和滑动面以上的上下游水压力、扬压力、岩体自重等，排水幕区域透渗压力以参数a=0.25折减。

3 模拟计算结果与解析

3.1 响应力与移位解析

本文重点对溢流段实施深层稳定抗滑性探究，参考前述建模，分别对核校洪水位、设计洪水位、一般高水位3种工况实施响应力及移位计算解析。

3.1.1 正常蓄水位工况计算

正常蓄水位计算结果云状态图见图3-图8。

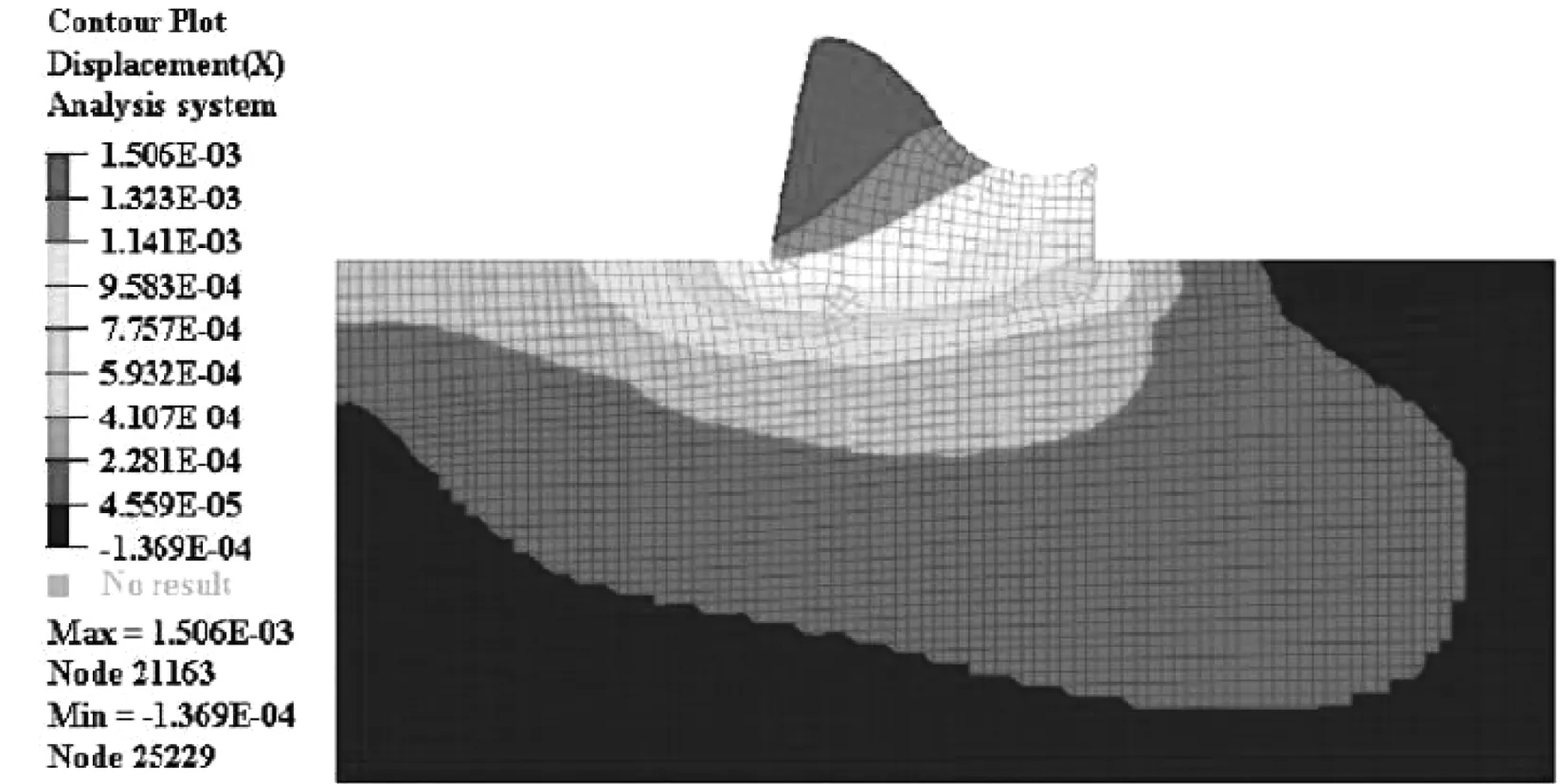
图3 取自X方向的移位云状态图

图4 取自Y方向的移位云状态图

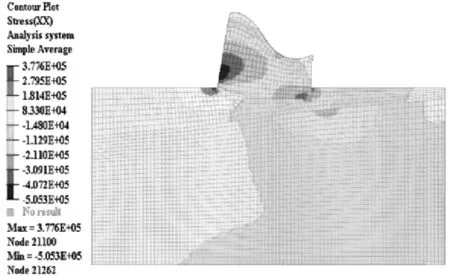
图5 总移位云状态图

图6 取自X方向的应力云状态图

图7 取自Y方向的应力云状态图

图8 基于Mises 的应力云状态图

1) 正常蓄水位工况移位分析：从图3可以看出，坝身上游侧的X向最大移位为1.5 mm，这缘于上游侧静水压和上游水体重量大量施加于坝面，在X方向上的分量较大，导致其X向的形变也较大。从图4可以看出，下向的最大移位出现在下游侧坝身，最大移位0.89 mm，出现在反弧段与坝趾结合部位。坝身上游侧Y向移位为0.79 mm，略低于下游侧坝身的移位。从上至下，Y向移位量渐渐降低，深坝基的移位几乎为零。从图5可以看出，在静水压、淤泥压和坝身自重等载荷联合作用下，坝身整体构造呈下陷的态势，最大移位出现在坝身上游侧，位处堰顶位置，最大移位1.66 mm，方向为下向，浅坝基移位要高于深坝基。

2) 正常蓄水位工况响应力分析：图6、图7及图8分别给出了坝身与坝基在静水压、水重、淤沙压力、扬压力和坝身自重等联合作用载荷下整个构造的X方向响应力、Y方向响应力和mises响应力分布云状态图。绝大部分区域第一主响应力为压响应力，所有位置第三主响应力均为压响应力，溢流段的基础底部法向响应力均为压响应力。从图6可以看出，X向最大响应力为0.51 MPa，发生在坝身上游侧底部。从图7可以看出，Y方向最大响应力发生在坝身上游侧底部，为0.36 MPa，属于局部集中响应力，由于上游水体压是从上至下渐渐加增，因此底部Y响应力最大。从图8可以看出，最大mises响应力发生在坝身上游侧与浅层基础结合处，约为0.56 MPa，整个构造没有发生弹塑性形变。此外，在坝身与浅坝基、浅坝基与深坝基交界处都会发生响应力的梯度演变，这基本是不同材料机能参数差异导致的。

3.1.2 设计洪水位工况计算

设计洪水位云状态图见图9-图14。

图9 取自X方向的移位云状态图

图10 取自Y方向的移位云状态图

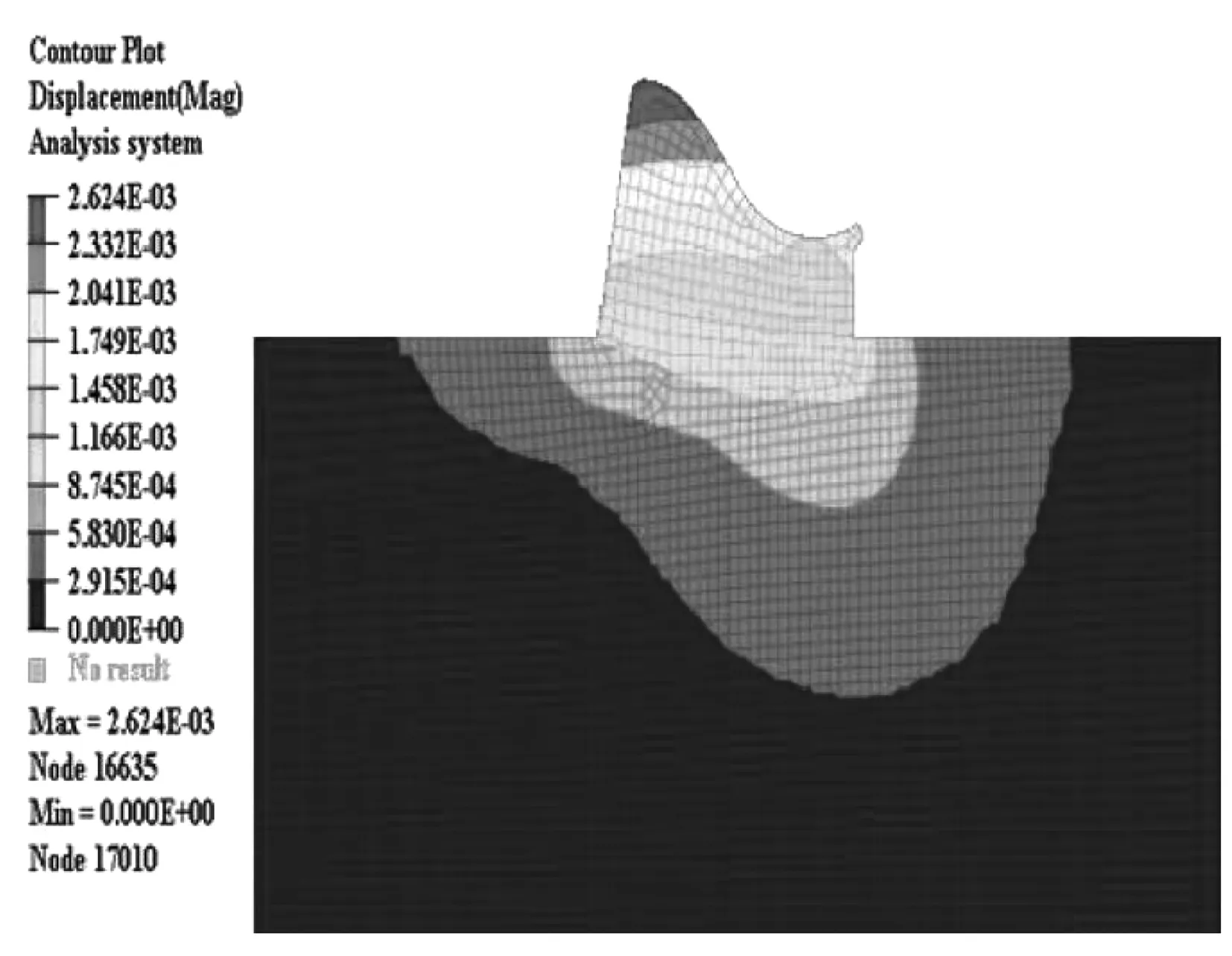
图11 总移位云状态图

图12 取自X方向的应力云状态图

图13 取自Y方向的应力云状态图

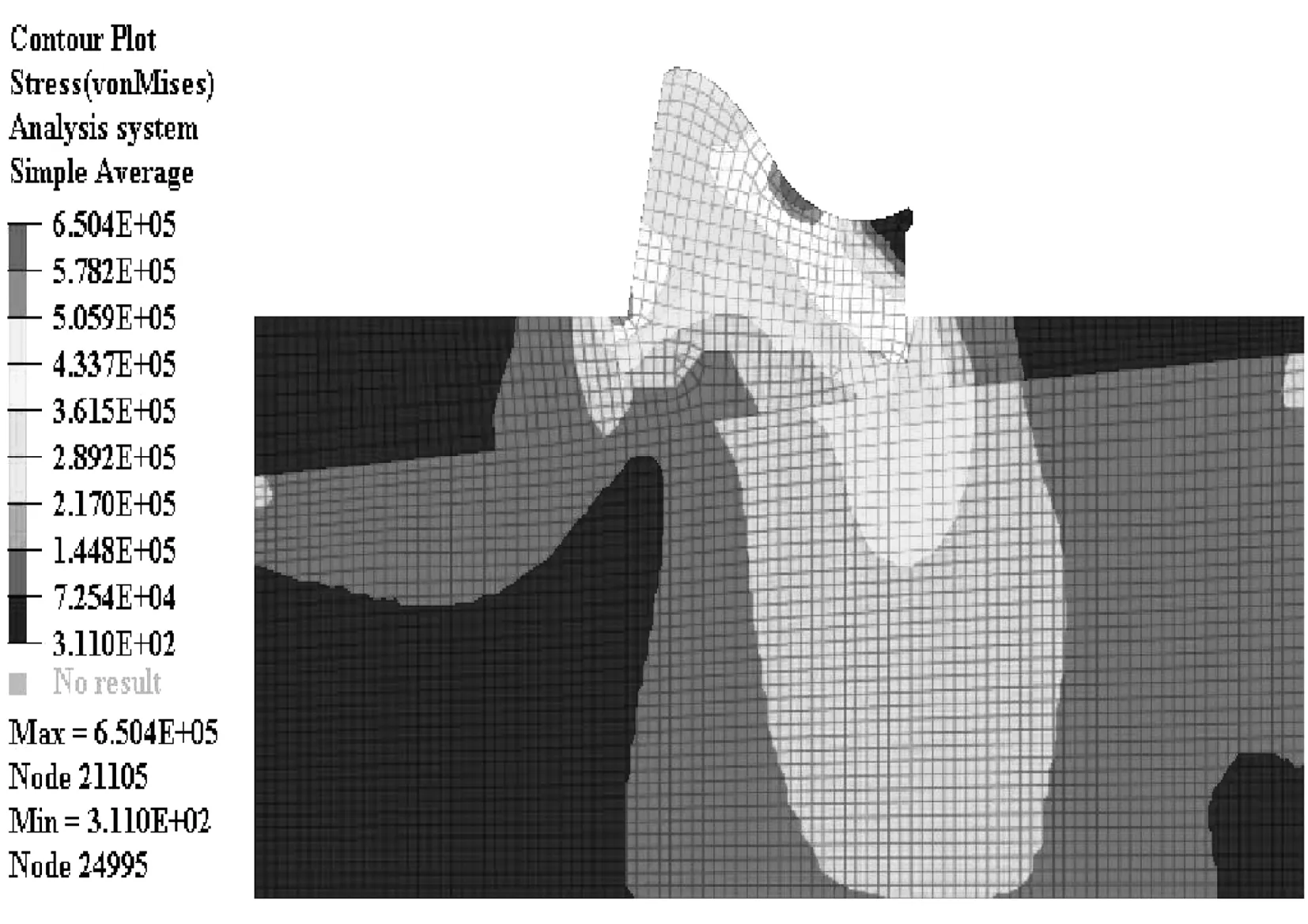
图14 基于Mises 的应力云状态图

1) 设计洪水位工况移位解析：由图9可知，在坝身自重、淤泥压和静水压等载荷共同作用下，构造整体呈下陷态势，移位最大值出现在坝身上游侧，移位量为2.62 mm，浅坝基移位量较深坝基移位量要高。从图10可知，最大下向移位出现在坝身下游侧，移位量为1.08 mm，坝身上游侧Y向移位较坝身下游侧的移位量略低，移位值为0.24 mm。从上至下，Y向移位量渐次降低，深坝基移位几乎零值状态。从图11可以看出，坝身上游侧X向移位最大量为2.6 mm，这缘于上游侧水体重量和静水压是向坝面垂直施加上的，在X方向上存在较大的分量，致使其X向的形变也较大。

2) 设计洪水位工况响应力分析：图12、图13及图14分别给出了坝身与坝基，坝身在水体自重、坝身自重、扬压、静水压和沙淤压等联合载荷作用下的mises响应力Y向响应力和X向响应力云状态图。第一主响应力在绝大部分区域均为压响应力，第三主响应力在所有位置均为压响应力，溢流段的基础底部法向响应力均为压响应力。由图12可知，最大X向响应力为0.48 MPa，在坝身下游侧坝趾及反弧段位置，呈响应力局部集中状态。由图13可知，最大Y向响应力为0.43 MPa，发生在坝身下游侧坝趾和反弧段位置，呈响应力局部集中状态。由图14可知，最大mises响应力约为0.65 MPa，发生在坝身下游侧位置，整个构造没有发生弹塑性形变。而且，在深坝基与浅坝基、浅坝基与坝身的交界部位，均发生了梯度响应力演变，此为不同材料机能差异所导致。

3.1.3 核校洪水位工况计算

核校洪水位计算结果云状态图见图15-图20。

图15 取自X方向的移位云状态图

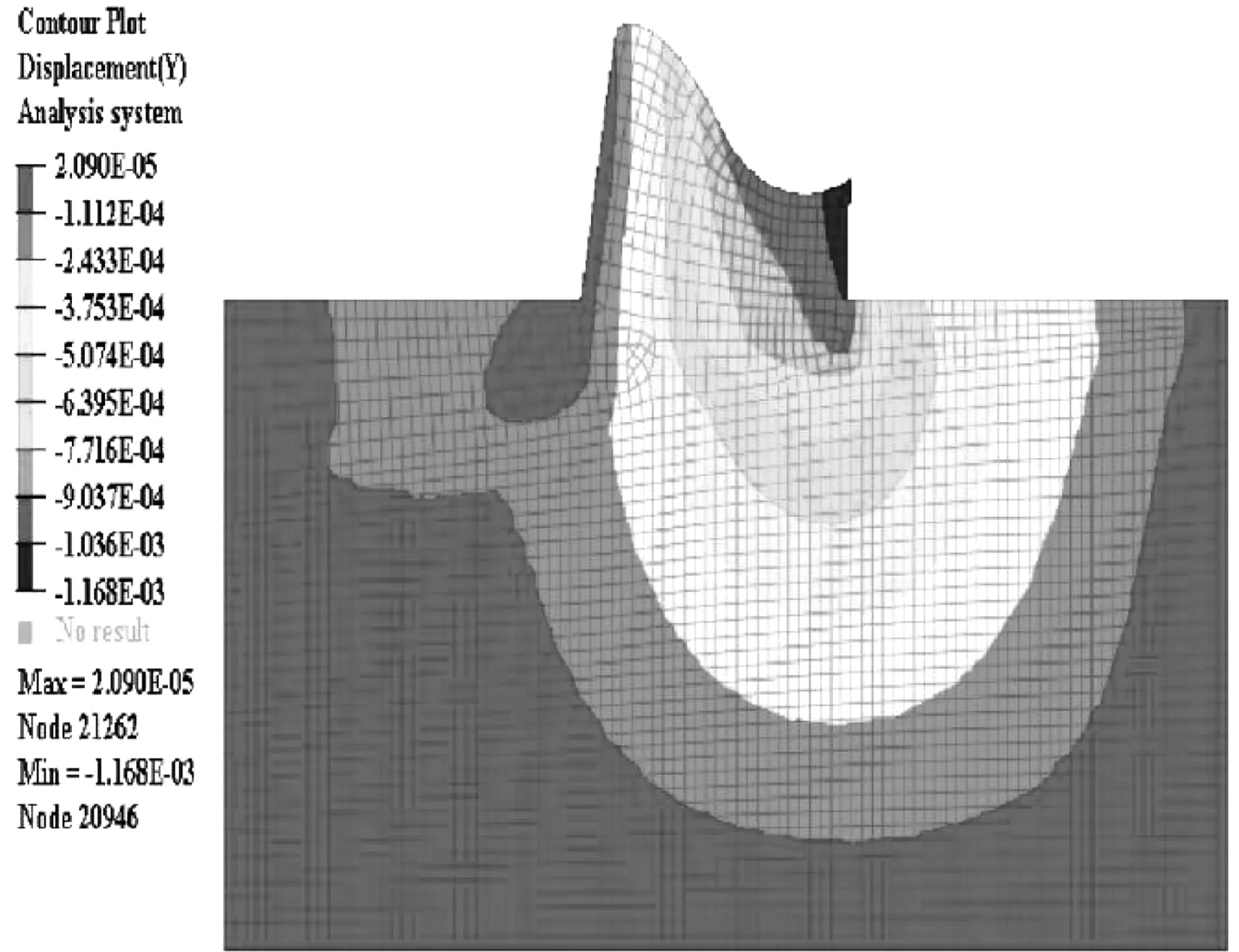
图16 取自Y方向的移位云状态图

图17 总移位云状态图

图18 取自X方向的应力云状态图

图19 取自Y方向的应力云状态图

图20 基于Mises 的应力云状态图

1) 核校洪水位工况移位分析：从图15可知，在坝身自重、淤泥压和静水压等载荷共同作用下，坝身呈下陷的态势，移位最大量为2.86 mm，出现在坝身上游侧，浅坝基移位较深坝基移位要相对大些。由图16可知，最大下向移位量为1.17 mm，出现在下游侧坝身，坝身上游侧Y向移位量为0.24 mm，较下游侧坝身移位略低。从上至下，Y向移位量呈逐渐降低状态，深坝基移位几乎零值。由图17可知，坝身上游侧的X向最大移位量2.86 mm，缘于上游水体重量和静水压是垂向施加于坝面，在X方向上存在较大的分量，致使X向的形变也较大。

2) 核校洪水位工况移位分析：图18、图19及图20分别给出了坝身与坝基，坝身在水体自重、坝身自重、扬压、静水压和沙淤压等联合载荷作用下的mises响应力、Y向响应力和X向响应力云状态图。第一主响应力在绝大部分区域均为压响应力，第三主响应力在所有位置均为压响应力，溢流段的基础法向响应力均为压响应力。由图18可知，最大X向响应力0.54 MPa，发生在坝身下游侧反弧段位置。由图19可知，Y向响应力最大值为0.5 MPa，发生在坝身下游侧坝趾位置，属于响应力局部集中，缘于上游水压系由上至下逐渐加增，因此导致最大底部Y响应力。由图20可知，最大mises响应力约为0.72 MPa，发生在坝身下游侧，整个构造没有发生弹塑性形变，属于正常状态。在深坝基与浅坝基、浅坝与基坝身交界部位发生响应力梯度演变。

3.2 稳定抗滑分析

将有限元方法计算结果与常规极值刚体平衡法所得结果开展比对，以验证有限元模拟结果的正确性，见表3。

表3 溢流坝深层稳定抗滑分析成果

模拟计算成果分析：

1) 各节点受力程度有所不同，因为坝身上各节点和滑动面在诸种载荷联合作用下，应力状态相对复杂，所以对应安全抗滑常数也就有所不同。但滑动面坝基的安全系数总体满足于重力坝的设计规范需要。

2) 两种方法获得的重点安全系数总体一致，均胜任重力坝基本设计规范的要求，因此重力坝稳定抗滑分析以有限元法来试算验证是可行的。

3) 有限元法计算坝体深层稳定抗滑系数，所得数值较极值刚体平衡法所得数值略高。查阅资料可知，极值刚体平衡法取计算截面系单宽最大截面，计算所得安全系数相对于有限元法的安全系数要小，其稳定性能相对低些，但仍在相对安全的范围内，可以满足设计需要。

4) 借助ANSYS专业智能系统模拟计算重力坝深层稳定抗滑系数，智能快捷，操作性强。能够通过更换不同的工况和参数，实施多工况条件的模拟演算，相较于传统方法，相对省时省力效率高。而且经过数据导出，能够获得整体安全系数和每个节点的安全系数，对坝身稳定抗滑性能作多角度、相对大规模的数理模拟分析，可以使分析结果更典型、精确和具体，利于工程应用。

4 结 语

本文参考案例实用技术数据，借助ANSYS专业智能有限元模拟系统，围绕溢流段坝体深层稳定抗滑性态，对混凝土埋石重力坝深层抗滑课题开展了专题分析研究：①建立了混凝土埋石重力坝深层抗滑有限元模型并开展了模拟分析计算；②开展了混凝土埋石重力坝深层响应力与移位、稳定抗滑性专题解析；③模拟分析验证了有限元法在计算重力坝深层抗滑系数上的适用性，可为同类工程应用提供一定意义的技术参考。