结合面微观接触面积分布数值仿真分析方法

苏 蕾，荆建平，2

( 1.上海交通大学 机械系统与振动国家重点实验室，上海200240；2.上海交通大学 燃气轮机研究院，上海200240)

机械系统通常由各个零部件通过诸多结合面之间的配合连接构成。任何零件表面在微观下都不是绝对光滑的，存在几何形貌的偏差，实际接触只在存在于较高的微凸体上，因此两粗糙面构成的结合面实际接触面积必然远小于配合面的面积。结合面的静、动态特性直接影响整机的刚度、阻尼等[1]，进而影响整机振动、噪声等特性。因此要获得更可靠的整机特性必须加深对结合面的微观接触特性的研究。

结合面接触研究由来已久，早期研究将Hertz理论用于单个接触点研究，假设粗糙面由等高但相互独立的微凸体构成，所有微凸体产生相同的弹性变形[2]。由于粗糙表面微凸体的等高分布与表面实际轮廓不符，Greenwood 和Williamson[3]提出基于统计分析的接触模型，假设粗糙峰高度随机。根据粗糙面的分形特征，Majumdar 和Bhushan 提出以分形函数为基础的接触模型。Komvopoulos[4]提出修正的MB 接触模型，并指出结合面真实接触面积只有名义接触面积的1%或更少。Jiang[5]根据分形理论建立了结合面法向接触刚度模型，并与试验数据对比。李小鹏[6]等建立了引入摩擦因素的结合面刚度阻尼模型。

MB 分形接触模型是目前国内外研究人员分析结合面接触状态的常用模型。本文以MB分形接触模型为基础，在粗糙表面形貌的有限分形嵌套的实际情况下，依据W-M函数的最大空间频率以连续可导曲线表征分形特征。提出接触面积分布的数值求解方法，通过仿真直接求得分形函数描述的粗糙面与平面接触的面积分布，并与早期研究的分布函数对比。

1 粗糙面微观形貌描述

以往学者通过对粗糙面实测轮廓的研究发现粗糙表面轮廓曲线具有统计意义上的相似，即无规则分形特性。传统欧氏几何的各类粗糙度系数难以全面表征粗糙表面形貌的特征。随机化的Weierstrass函数是不同频域下的几何累加，Mandelbrot 以此为基础构造了具有分形特征的函数——W-M 函数[7]，其表达式如公式(1)所示。分形几何为基础的W-M函数利用不同波长和振幅的余弦波相互叠加以表征粗糙表面轮廓更完整的形貌特征，因此广泛应用于粗糙面接触问题。该函数具有处处连续但不可导、自仿射等特性，图1为该函数模拟出的轮廓曲线

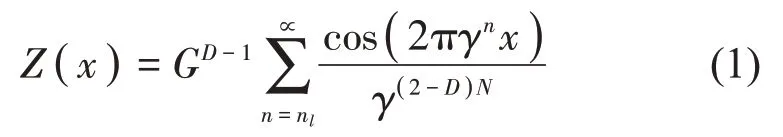
Z——表面轮廓高度；

x——表面轮廓位置坐标；

G——特征尺度系数；

D——分形维数；

γn——轮廓空间频率，γ为大于1的常数，高斯分布的随机轮廓一般γ取值为1.5；轮廓最低频率γnl≈1/L，其中L为粗糙面样本的长度。

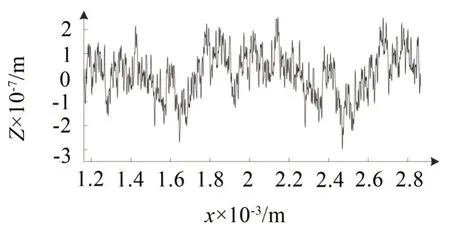
图1 W-M函数模拟轮廓曲线

2 MB分形接触模型

机械系统中结合面的真实状态是两不光滑的表面相互接触，具体表现为具有分形特征粗糙面与粗糙面的接触，如图2所示。下表面轮廓高于上表面轮廓的阴影部分为两粗糙面的实际接触变性部分。

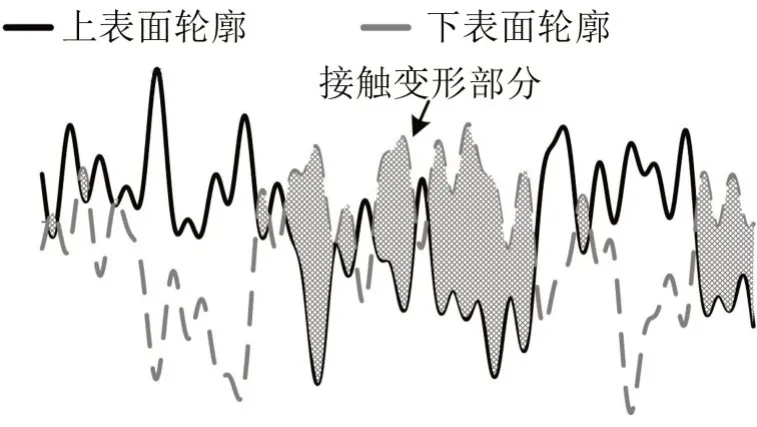
图2 粗糙面与粗糙面接触模拟图

Majumdar 和Bhushan[8]提出基于分形几何的粗糙表面接触模型，将无摩擦情况下两粗糙表面的静态接触问题简化为理想刚性平面与粗糙平面的接触，并且忽略材料硬度随表面深度的变化和相邻微凸体变形产生的相互作用，如图3所示。该模型以W-M分形函数和全球岛屿截面积分布规律为基础，假定微凸体的曲率半径与表面轮廓有关，使得模型具有尺度独立性。

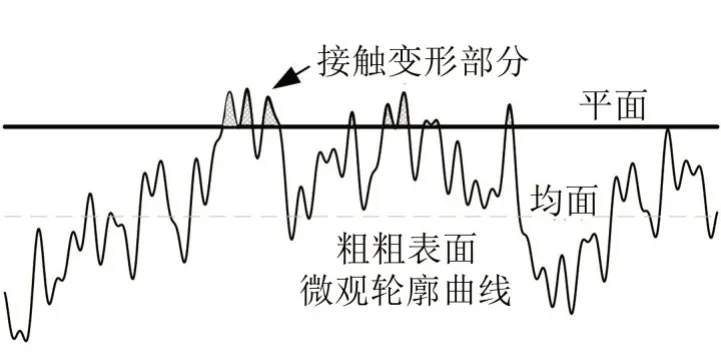
图3 粗糙面与刚性平面接触模拟图

MB 模型将两相互无摩擦的粗糙平面受载情况下的静态接触简化为各个独立的微凸体与刚性平面的接触问题。根据hertz接触理论，微凸体发生弹性变形，实际接触面积at为变形前微凸体与平面截面积a的一半[9]。单个微凸体接触模型如4所示。

Mandelbrot[10]研究全球岛屿形貌时发现，设岛屿与海平面的截面积值为A，所有岛屿中A大于一定值a的岛屿数量为N，则N与a存在幂律关系。图5为岛屿示意图。

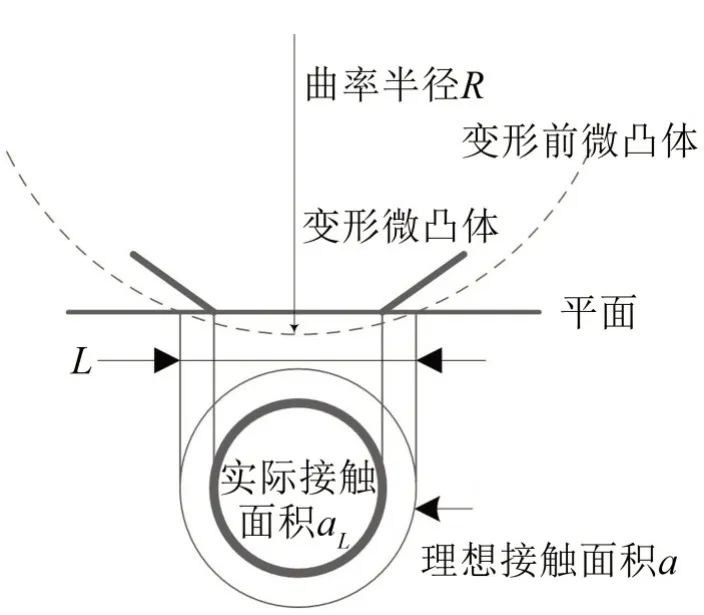
图4 微凸体接触模型

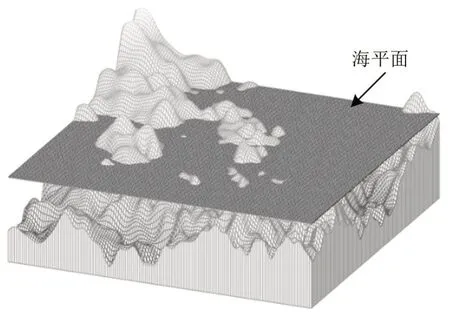
图5 岛屿示意图

Majumdar[8]根据岛屿最大截面积为aL且个数为1，提出的面积分布函数如公式(2)所示

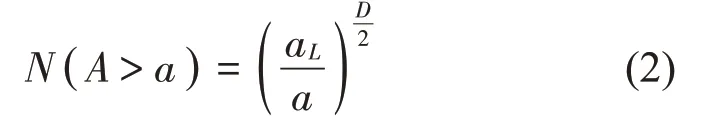
其中：D为岛屿分布规律的分形维数。对其进行微分，可得截面积分布函数如下

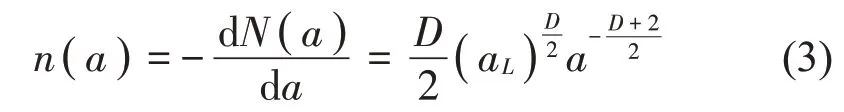
MB 分形模型以此表示分形表面微凸体的截面分布情况，由上述分布函数求期望可得分形表面与刚性平面总的截面积A为

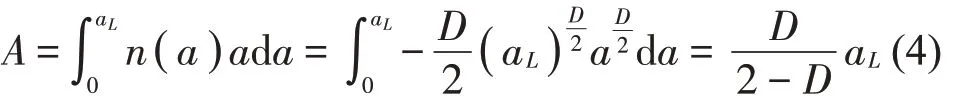
MB 模型中假定微凸体截面积的分布函数仅在(0,aL]内非零，K.Komvopoulos[6]提出对原始微凸体接触截面面积离散分布函数的非零域合理近似扩展。其假设只有一个最大接触截面积为aL，将分布函数在a=aL邻域内替换为迪利克雷函数，定义区间扩展因子ψ，进而提出了更加精确的分形表面微凸体截面面积分布修正函数，如公式(5)所示

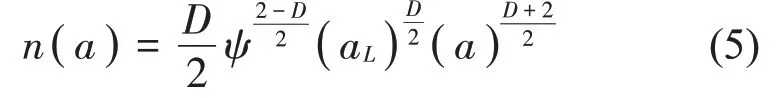
并提出D与ψ的关系如公式(6)所示

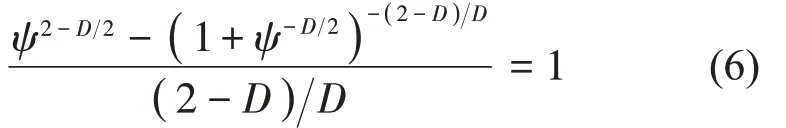
对n(a) 积分求原函数可得数量N与面积a的关系如公式(7)所示。

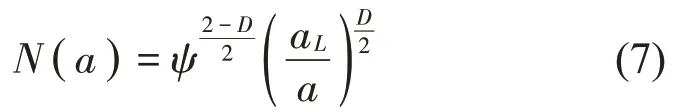
公式(7)相比与公式(2)多了系数ψ，根据公式(6)可知ψ与分形维数D一一对应且取值范围[1.718，2.618]，因此公式(7)所表达的接触点面积分布仍只与分形维数D和接触点最大面积aL相关。

3 接触截面分布的数值计算方法

3.1 分形轮廓曲线的简化

自然界的分形与数学上的分形几何相比具有两个特征。其一，自然界中的分形仅在一定尺度范围、一定层次中才表现出分形特征；其二，数学上的分形可以具有无限层嵌套结构，而自然界的分形多是统计自相似的，仅有有限次的嵌套结构[2]。因此，W-M函数中三角函数项只需做有限次的叠加，即正整数n不能取到无穷大，存在最大值nmax.轮廓最大空间频率与仪器分辨率有关γnmax≈1/Re，即仪器能达到的最大采样频率。

数学上的分形几何中，因为存在无限次嵌套，所以W-M函数具有处处连续但不可导的特性，但对于表面形貌的具体问题，限制最大嵌套次数后，函数即具有连续可导的特性。

利用Majumdar 和Tien 在1990年[7]模拟粗糙表面的一组数据：扫描长度L为4 mm、仪器分辨率Re为5 μm、特征尺度系数G为12.445 nm、分形维数D为1.882。根据样本长度和仪器分辨率计算得到nmin=14，nmax=30，将以上各参数带入W-M函数的公式模拟粗糙表面。因为x=0 点时余弦函数值恒为1，与n无关，不具有一般性，为避开x=0点，所以此时x的范围取5×10-5～4×10-3m。图6为步长分别为5×10-6m和2×10-8m 的模拟轮廓曲线，即以仪器分辨率为采样频率和其他更高的采样频率分别模拟。

因为步长为5×10-6m时采样点个数远小于W-M函数的最高空间频率γ30≈191 751，所以显示的模拟轮廓线是首尾相连的折线。根据当前条件下WM函数连续可导的特性，将步距取为2×10-8m，从而使得采样点个数大于最高频率，可以获得连续轮廓曲线。实测表面轮廓受仪器采样频率的限制，由图6可看出，采样点不足时难以表征函数完整特性。根据图7给出的轮廓高度分布规律，采样点大量增加并不会影响轮廓高度的分布规律(高斯分布)，在统计上仍具有相同的特性，且MB 模型假设各微凸体相互独立。因此后续研究利用大量采样点以获得函数完整特征，即利用连续可导的曲线模拟粗糙面轮廓。

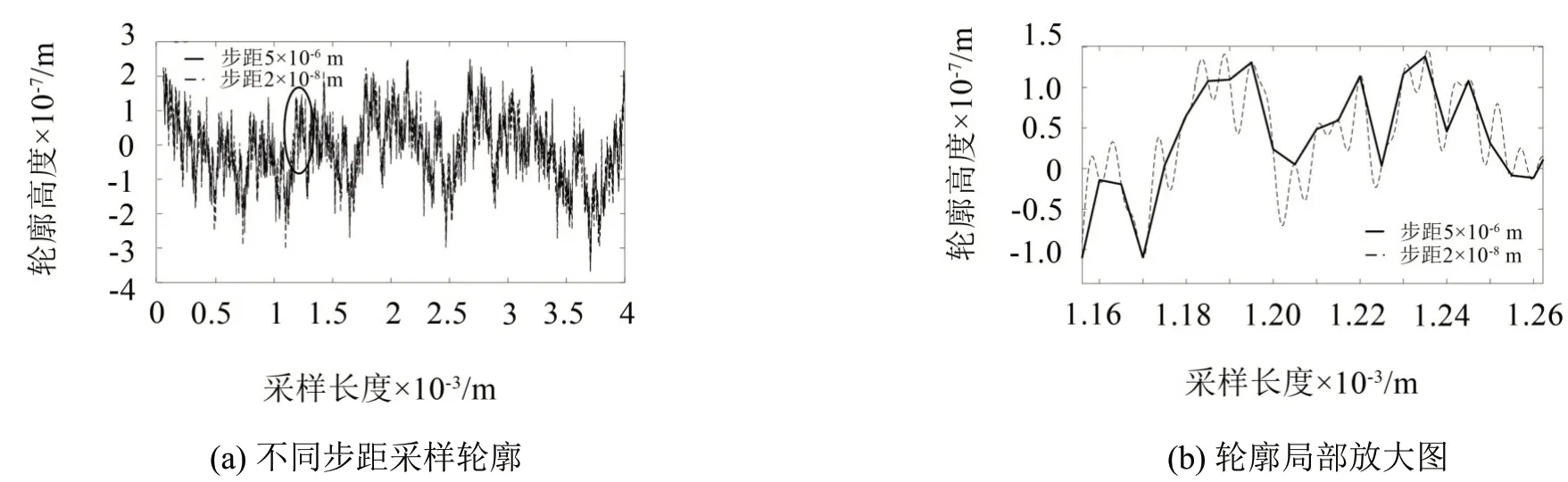
图6 限定空间频率的W-M模拟轮廓曲线

图7 轮廓高度分布规律

3.2 微凸体截面积的求解

根据MB接触模型的假设，建立如图8的二维简化接触模型，利用3.1 中的参数模拟分形曲线，刚性平面与水平线距离为h。截线长度L即对应微凸体截面的理想直径，由此可获得理想截面积。

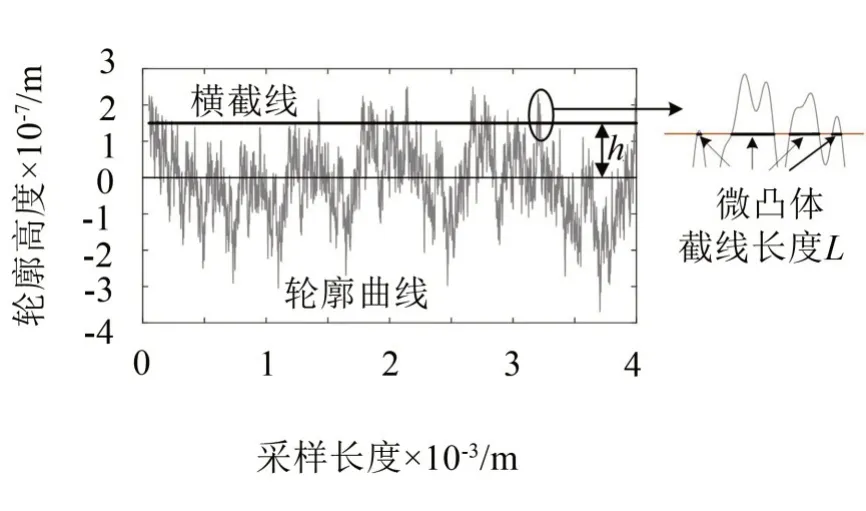
图8 分形接触轮廓模型

求得所有轮廓峰与截线的截断长度，需先求得峰值高于h的极大值点。通过限定叠加次数的W-M函数，生成连续可导的光滑曲线，求出曲线的极大值即为轮廓的峰值，利用极值点与截线高度求得截断长度。由于函数过于复杂，且需要求解所有极大值点，传统求导获得极值的方法难以实现，只能利用数值解法。

一般算法都是求解函数最值，诸如遗传算法、模拟退火算法、梯度下降法等，避免获得局部最值。本研究为了获得所有峰值，采用将函数分段，在每段上求解最值，当区间划分足够精细时，每个小区间内最多只有一个极值，从而获得所有极大值点。为降低计算量，先判断区间是否存在极大值点然后再求解，根据区间前提条件，若存在极大值则左端点导数大于零、右端点导数小于零，如图9所示。

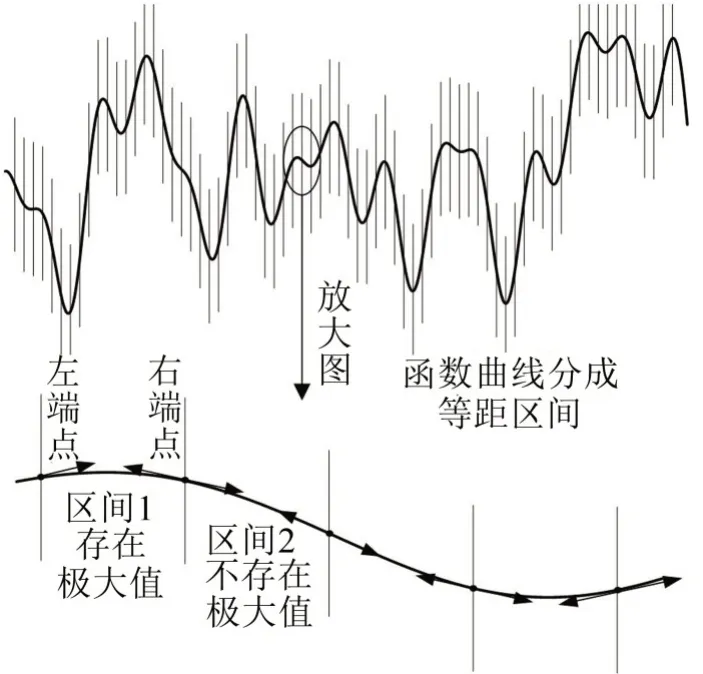
图9 分段区间求极大值

对限定截止频率后的W-M 函数求导获得梯度计算公式(8)

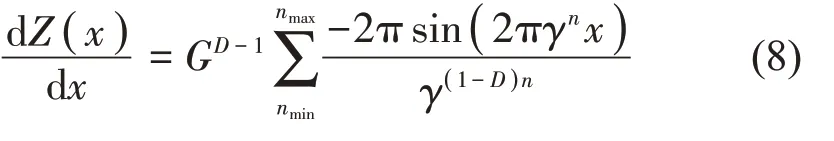
利用梯度上升法求极大值，本文构造爬坡算法，如公式(9)，其中a为步长，为加快求解速度需设置动态步长。

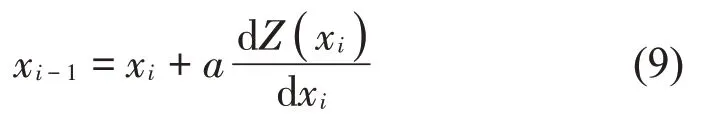
为判断所求结果是否正确，验证极值点的梯度并将区间进一步缩小再次求解，所得极值点个数基本无差别，极大值点均已获得。

根据所获得的极值点，若某点的值大于h，即与截线相交。构建求解算法，如公式(10)所示，从极值点出发，若前两步对应F值的符号相同则β等于0，否则等于1。反复迭代求得极值点左右最近的高度等于h的点，左右两点间的横坐标差即近似为截线长度，遍历所有符号条件极值而获得所有截线长度。

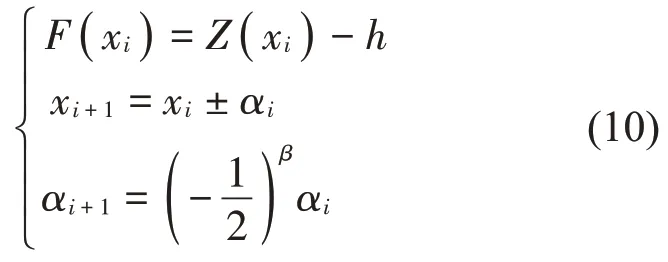
相邻极值点可能解得同一条截线，如图10所示。

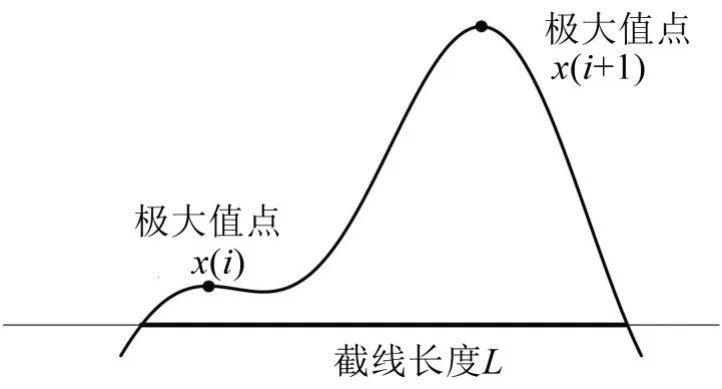
图10 相邻峰值点得同一段截线

计算过程中需要去除相邻峰值点计算获得重复的截线，否则不能反映真实分布情况。

3.3 面积分布规律分析

根据前述分析，求得的所有截线长度L，即为与平面相交的各微凸体的截面理想直径。公式(2)与公式(7)中幂运算的底数均为aL/a，且易知aL/a=(Lmax/L)2，因此可根据所得截线长度进一步获得利用W-M 函数模拟曲面与平面接触状态的截面分布规律。数据处理过程中去除奇异值，获得(Lmax/L)2以及与之对应的长度大于L的个数N。取3.1中模拟分形轮廓的参数，h取1.5×10-7m时求得接触点面积个数分布如图11所示。

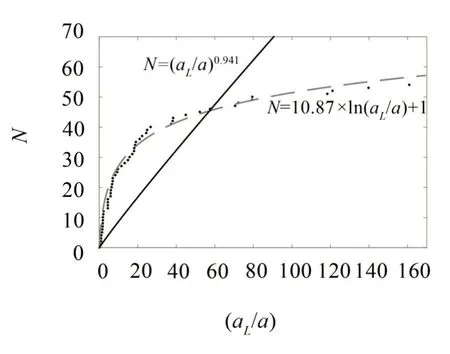
图11 不同函数拟合所得曲线

利用公式(2)，以D作为待求参数拟合离散点，求得D的值约为1.746；利用公式(7)拟合，求得D值约为1.7；模拟轮廓所用分形维数1.882 均接近两公式你拟合获得的值，误差分别为7.8%、10.7%。

表1所示为分形维数1.882 的粗糙面轮廓曲线与平面在不同名义距离下，求得接触点面积分布对应拟合方程参数。当距离较远时，所得参数D与分形维数更接近，且拟合曲线的均方根误差（RMSE）较小，即可信度高；距离较近时，拟合所得结果误差较大，且拟合曲线的RMSE也较大。

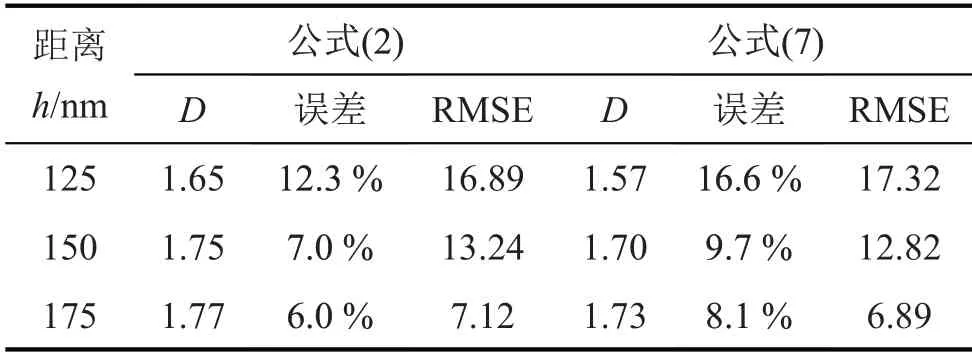
表1 平面与曲面不同距离求得分布函数

如图8所示，大接触点是由小接触点的叠加获得，平面距离较近时，发生弹性变形的部分相对更多。多个接触点的合并成一个大接触点，导致局部接触点数量减少，部分接触点面积变大，因而求解得D的值相对较小且拟合的均方根偏大。

如图11所示，公式(2)的拟合效果并不好，本文提出对数形式的面积分布函数，如公式(11)所示。利用此公式拟合各点，所得曲线更贴近离散点的分布。

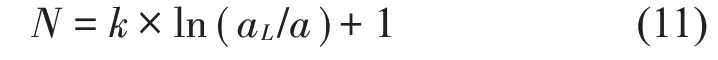
对不同D所描述的模拟粗糙面轮廓曲线，求得接触面积分布离散点，进而求得对应的参数k，D与k的关系如图12所示。

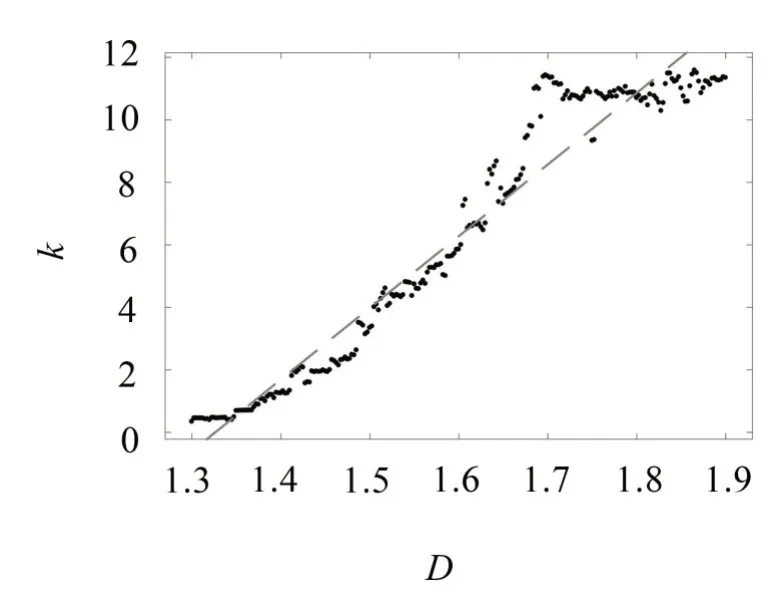
图12 参数k与分形维数关系

参数k与分形维数D呈近似线性关系。当分形维数增大时，参数k增大，即接触点的数目越多，符合粗糙面的真实接触情况。

4 结语

本文以粗糙表面轮廓的分形特征为基础，根据模拟轮廓的W-M函数的最大空间频率，获得了连续可导的模拟轮廓曲线，并对函数模拟的粗糙轮廓与平面接触的面积分布开展数值计算及统计分析。利用数值方法求得轮廓极值分布，进而求得接触点面积分布情况，验证了MB 模型的分布函数近似符合W-M 函数描述轮廓的接触面积分布。研究结果表明存在对数形式的分布函数更符合接触面积分布，但其具体的参数仍需后续探讨。该数值方法通过求解直线与曲线相交部分截线长度获得分布规律，亦可求解两曲线相交部分的截线，因而该方法有望用于求解两粗糙面都具有分形特性的结合面接触模型的接触面积分布规律。