基于多重启动迭代扫描的需求可拆分车辆路径问题

闵嘉宁，金 成,2，陆丽君,3

MIN Jia-ning1 , JIN Cheng1,2 , LU Li-jun1,3

（1.无锡太湖学院，无锡 214064；2.南京航空航天大学 管理学院，南京 210000；3.南京大学 管理学院，南京 210000）

0 引言

需求可拆分车辆路径问题（Split Delivery Vehicle Route Problem，SDVRP）是由Dror和Trudeau[1]于1989年首先提出了。在SDVRP中，到需求点的交货可以进行拆分、由多辆车完成送货[1,2]。因此，VRP可以根据使用的车辆数量和行驶距离进行优化，SDVRP迅速成为VRP的重要分支，受到越来越多的关注[3]。

学者们提出了启发式、元启发式和多阶段/混合启发式算法对SDVRP进行求解[3]。Dror和Trudeau[1,2]在假设每个i的di≤Q的情况下提出了局部搜索算法，引入了两阶段操作：第一阶段，k-split，把对客户的访问分至不同的路径，每条路径具有足够的剩余容量，以满足拆分客户的需求。第二阶段，路径添加，考虑一个拆分客户，将其从访问它的所有路线中删除并创建一条仅含该客户的新路径。通过大量数值实验验证了：当任务点需求量较大时，SDVRP的结果明显优于VRP。Archetti等人[4]提出了第一个禁忌搜索算法（Tabu Search algorithm，TSA），称为SPLITABU。实验表明，SPLITABU比Dror和Trudeau[1,2]算法更有效。Jin等人[5]提出了一种具有有效不等式的两阶段算法（Two-Stage with Valid Inequality，TSVI）：第一阶段，客户被划分为集群。第二阶段，在每一个集群中求解旅行商问题（Traveling Salesman Problem，TSP），确定最小旅行距离。所有集群的最小旅行距离之和用于迭代更新目标函数。Aleman等人[6]中，提出了一种两阶段算法。首先通过构造方法生成初始解，然后应用可变邻域下降（Variable neighborhood descent，VND）方案来改进初始解。在文献[4,5]和文献[7,8]提出的实例上对该方法进行了测试。Aleman和Hill（2010）[9]对[6]构建的两阶段算法进行改进，提出了一种用词汇构建方法进行禁忌搜索，随着搜索的进行，解决方案集在不断变化—在删除不良解决方案时，会向集合添加好的解决方案。该方法能够显著改善[6]的结果。Liu等人[10]提出了k-means聚类算法，并设计了两种不同的求解方法：一种是先分组后路径；另一个是先路径后分组。通过实验比较这两种方法，表明：先分组后路径的方法表现出更好的性能。Wilck和Cavalier[11]采用先聚类后路径的两阶段来解决SDVRP。为了实现比较合理的聚类，采用了三步操作：首先，选取离车场最远点，与车场组成一条初始路径；然后，将平均剩余容量舍入到最近的整数；最后，逐步向已构成的初始路径中加入最邻近的节点。他们的计算结果表明，在行程距离和计算速度方面，它在相同数据集下的性能较优。温真真[12]提出了一种三阶段局域搜索算法。首先，采用GENIUS求解全客户域的TSP路径，按照车辆的容量把路径分成若干个组，每个组都满足客户的负载量；然后，对每个点从它当前的路径中删除，采用点再插入贪婪算法，按照送货量拆分策略插入到最优位置，迭代直至无新的优化解；最后，通过扰动、重复上述“删除-再插入”直至得到最优解。实验表明该算法可以获得较好的结果。向婷等人[13]提出了一种先分组后路径的两阶段算法，首先基于“最近”原则，通过设置分割阈值来限制一定范围内的车辆负荷，然后采用蚁群算法对路径进行优化。石建力等人[14]提出了一个随机客户的SDVRP模型。采用改进的分割插入算子和自适应大邻域搜索启发式算法。Shi等人[15]提出了一种基于局部搜索的粒子群方法。设计了编码解码方法和最佳位置向量，对SDVRP方案进行了优化。

在上述研究中采用的各类启发式方法通常很耗时，而大多数精确算法仅可在小范围内求解SDVRP。为了解决这些问题，在本研究中，提出了一种基于多重启动迭代扫描算法（Multi-Restart Iterative Sweep Algorithm，MRISA）的两阶段方法，首先，将所有客户点按照车辆的最大容量划分成组，采用适当的负载率（Load Factor，LF）和阈值系数（Threshold Coefficient，TC）对已获得分组进一步微调优化；然后采用禁忌搜索算法TSA优化每组的路线。基准数据的计算实验表明，该算法可以在几秒钟内获得近优解。

1 问题描述

在SDVRP中，车辆从车场出发，为客户提供送货服务，最后返回车场。当车辆为顾客服务时，访问次数没有限制，也就是说，每个顾客可以由同一车辆或不同车辆访问多次。求解一组车辆路径，在车辆容量限制下使用的车辆数最小并且总行驶里程最小。

SDVRP是一个无向图G=（V，E），其中V是顶点集，E是边集。假设在所考虑的SDVRP中有n个客户和m辆车。客户为i=（1，2，…，n），i=0表示车场，车辆为v=（1，2，…，m），车队中的车辆是同型号的，车辆最大负载量为Q。车辆从车场出发为客户送货，客户i的送货需求为di，客户i到j之间的送货量为dij≥0；客户i和j之间的距离为cij（cii=0，cij=cji，非负并满足三角不等式）；当满足所有客户的需求后，车辆返回车场。所使用的最小车辆数是其中[x]表示不小于x的最小整数。目标函数是求解合适的路径使得车辆行驶距离最短。决策变量是：

目标函数表述如下：

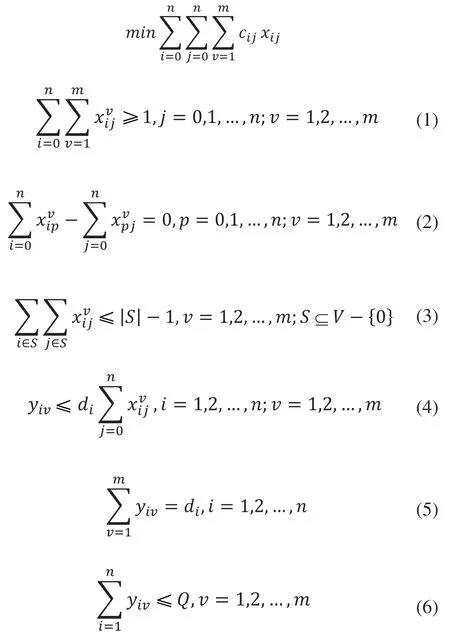
式(1)表示每个客户点必须至少访问一次。式(2)给出了流量守恒约束。式(3)给出了子路径消除约束。式(4)表示只有当车辆v访问客户点i时，客户点i才由车辆v提供服务。式(5)确保满足所有客户的需求。等式(6)确保每辆车不超过其最大负载能力。

2 提出的两阶段算法

该算法是一种基于先聚类后路径优化策略的两阶段算法。在第一阶段，使用MRISA将客户划分为集群，并确定每个分区中的分裂点。第二阶段采用TSA进行每个群集路线优化。下面对提出的MRISA+TSA算法作详细描述。

2.1 预处理

两阶段算法开始之前，首先对客户点di>Q的情况进行预处理：重量Q可以由一辆车运输，该点剩余重量di=（di-Q）参与以下程序处理的。

2.2 MRISA

扫描算法是Gillett和Miller[16]在20世纪70年代提出的一种构造式的启发式算法。它本质上将最近的客户划分为一个集群。为了满足SDVRP的要求，本文修改了经典扫描算法。采用确定分组的数量。使用多重启动迭代确定每个组的最后一个点和分割点。LF和TC用于微调优化组分区。MRISA的过程详细解释如下。

步骤1：转换坐标系

1）创建极坐标系。

2）将车场设置为极坐标系的原点。

3）将连接原点和一个客户点的线定义为角度0。

4）将所有客户点转换为该极坐标系。

5）按升序对客户点的所有角度进行排序。

步骤2：对客户域进行分区

步骤2.1：创建变量initialValue和storagePool。前者用于存储初始值，后者用于存储最佳值。

步骤2.2：第一次循环

1）将角度0的点设置为第一个起始点。

2）按顺时针（或逆时针）方向逐渐扫描将扫到的点放入该组，直到的累积值（Cumulative Value，CV）超过Q。将最后一客户点分成lp1和lp2；dlp1使当前组的总负载等于Q。该组以lp1结尾。

3）从点lp2（需求dlp2）开始下一组扫描。

4）重复(b)和(c)直到扫过最后一个点。

5）根据每个集群中点的空间分布计算总行程距离。

6）将总行程距离存入initialValue和storagePool.

步骤2.3：重新启动迭代

步骤2.3.1：顺时针扫描

1）按顺时针方向顺序设置每个点作为起始点。

2）执行步骤2.2（b-e）。

3）将当前总行程距离与storagePool中的值进行比较。如果storagePool中的值较高，则将其替换为当前值。

4）按客户点升序执行步骤2.3.1，直到到达最后一个点。

步骤2.3.2：逆时针扫描

1）以逆时针方向顺序设置每个点作为起始点。

2）执行步骤2.3.1（b和c）。

3）按客户点降序执行步骤2.3.2，直到到达最后一个点。

步骤2.3.3：应用负载率LF和阈值系数TC微调集群分区

1）通过微调负载率LF来调整集群分区，LF将Q更改为LF×Q。

2）设置TC（例如，2或4），进一步微调分区。

3）应用LF×Q和TC以后，步骤2.2(b)将CV的计算细化为多个控制分支，如表1所示。

步骤3：输出结果

1）输出initialValue和storagePool中总行程距离。

2）输出每个聚类中的点。

3）输出每个聚类中的拆分点和相应的拆分值。

2.3 路径优化

上述3.1和3.2执行后，问题域被分成几个较小的组。每组中仅有一条路径。采用TSA对每个组中的路径优化。TSA是Glover于1986年提出的元启发式算法。TSA的过程描述如下。

步骤1：初始化

1）设置关键变量：禁忌长度tabuLength，终止条件maxIter和禁忌表tabu[tabuLength]。

2）随机生成初始路径serialNum[customerNum]解决方案。

步骤2：计算serialNum的目标函数值并将其赋值给变量bestValue。

步骤3：如果迭代次数等于maxIter，则终止程序并输出最佳结果;否则，连续迭代，并执行以下步骤。

步骤4：通过采用合适的选择函数（例如，2-opts）生成当前解决方案的rr邻域。

步骤5：以非降序对这些 rr邻域进行排序，并将该列表存储在变量tempDist[rr]中作为候选队列。

表1 CV的控制分支

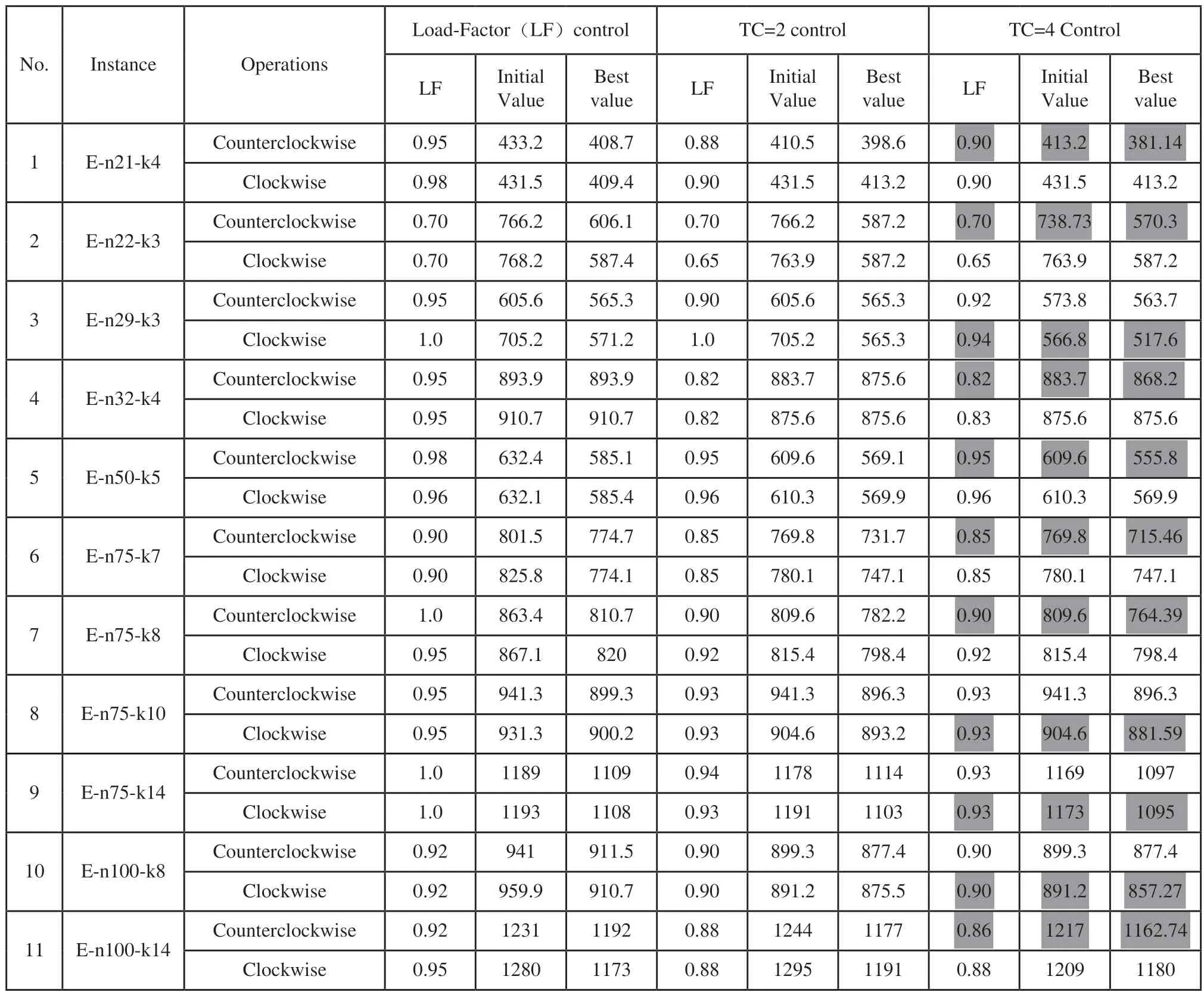
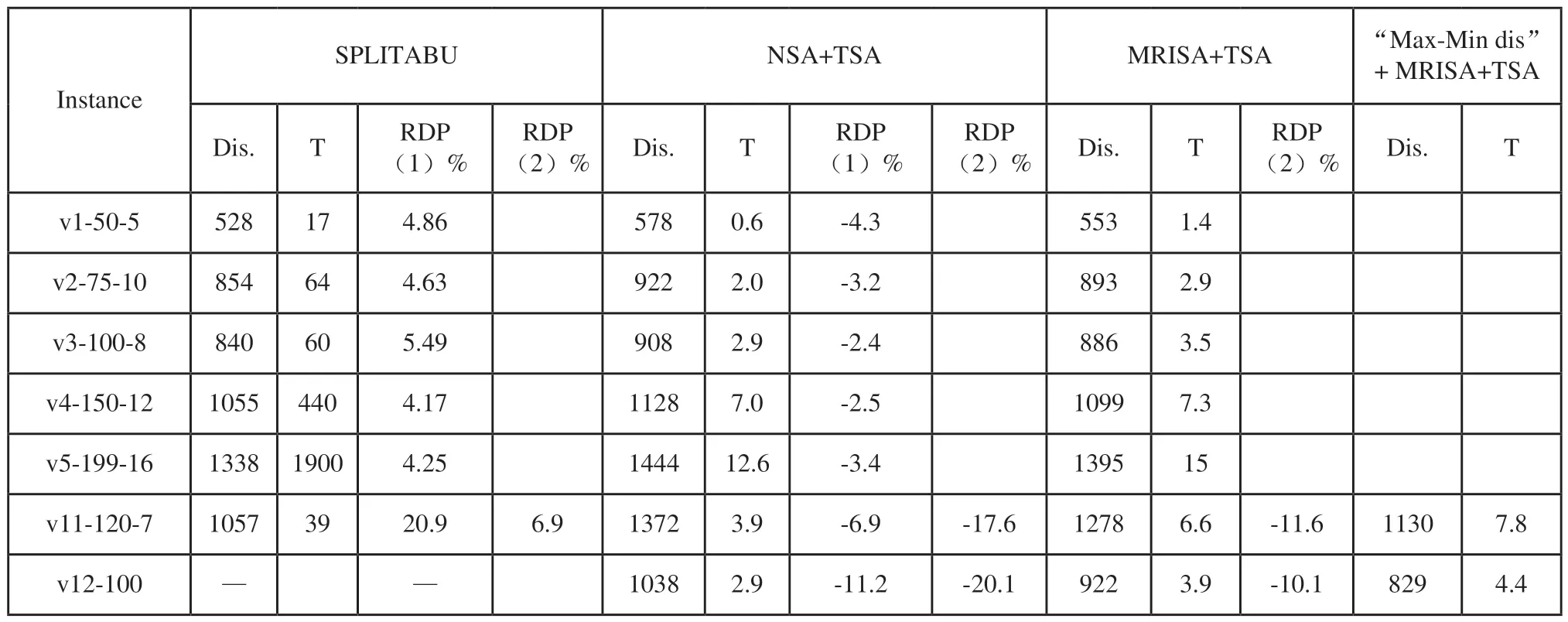
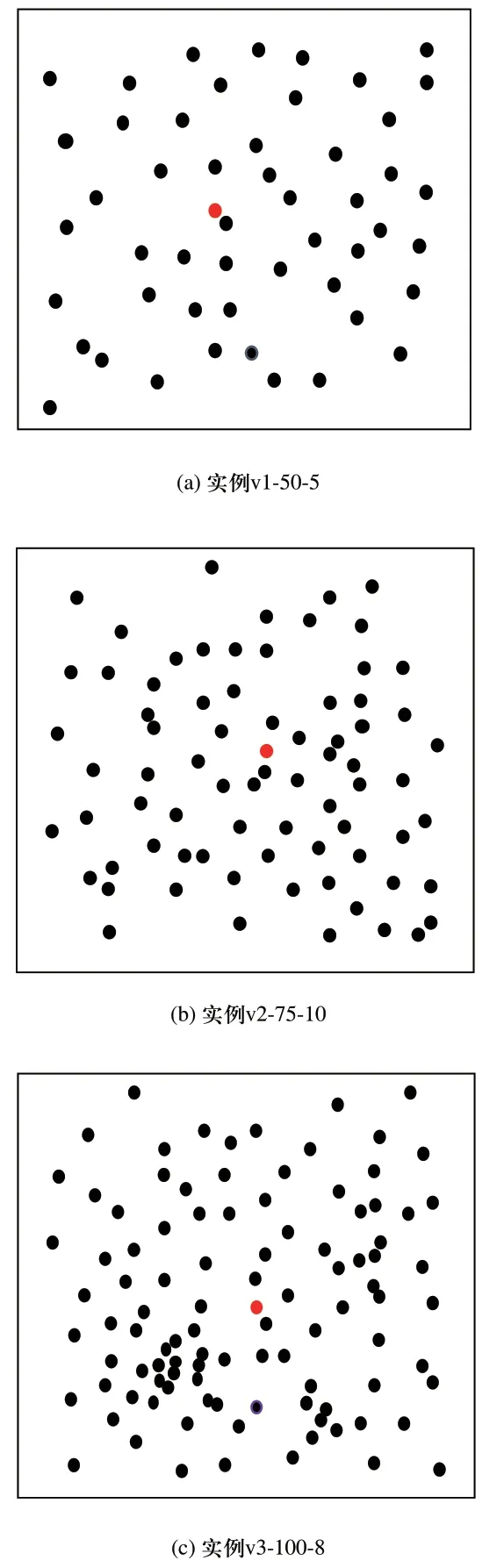
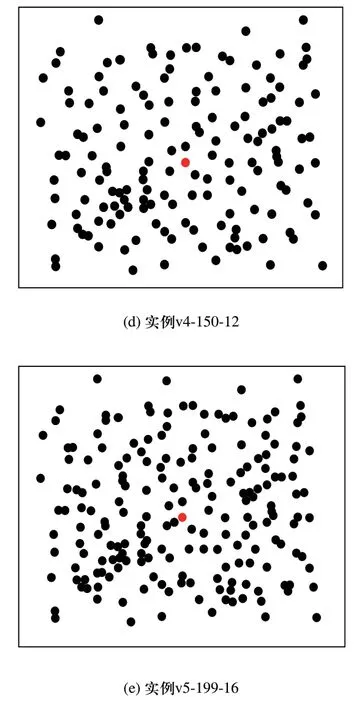
步骤6：如果tempDist[0]

1）用tempDist[0]替换bestValue和currentBestValue。

2）将bestQueue，currentBestQueue和tabu替换为tempDist[0]的相应对象。

3）返回步骤3。

否则，执行步骤7。

步骤7：分析 tempDist[rr]对应对象的Tabu属性

1）用tempDist[i]的最佳值替换currentBestValu（假设第i个）。

2）将currentBestQueue替换为tempDist[i].的相应对象。

步骤8：转到步骤3。

3 案例分析

为验证所提算法的可行性和有效性，在基准数据集上进行了相关实验。案例来源于VRP Web中CVRPLIB[17]，案例研究1使用了Christofides和Eilon基准数据集，案例研究2使用了Christofides，Mingozzi和Toth基准数据集。实验采用C语言、在64位Intel®Core处理器、8GB内存的Windows 7计算机上实现。

3.1 案例研究1

案例1数据集中有11个实例，如表1所示，实例名称“E-n21-k4”表示“Eil数据集，21点，4条路线”。对于每个实例，执行两个扫描操作：一个是顺时针的，另一个是逆时针的。在每次操作中，记录三个控制的结果，它们是：负载率LF控制，TC=2控制和TC=4控制。在每个控制分支列中，三个子列分别指示：负载率LF，初始循环中生成的初始值，以及MRISA的最佳值。表2列出了11个实例MRISA的实验结果。

表2的实验结果显示，1）每个实例在逆时针操作或顺时针操作的重启迭代中，行程里程发生变化；2）在任何一种操作中最佳值始终低于初始值；3）最佳值既可以出现在逆时针操作中，也可以出现在顺时针操作中；4）TC=4控制中的最佳值总是低于LF控制中相应的最佳值；5）在少数情况下，TC=4控制中的最佳值略低于TC=2控制中的值；而大多数情况下，TC=4控制中的最佳值与TC=2控制中的最佳值相等。这表明MRISA是必要的，可行的和有效的。

表2 11个实例MRISA的实验结果

3.2 案例研究2

案例2数据集中有6个实例，实例名称“v1-50-5”表示“vrpnc1 dataset，50 points，5条路径”。案例研究2比较了本文所提出的算法（MRISA+TSA）与基于正常扫描算法（Normal Sweep Algorithm，NSA）+禁忌算法的两阶段算法（NSA+TSA）以及SPLITABU[4]在案例2数据集上的执行结果。各种算法中记录了总行驶里程、计算所消耗的时间，以及行驶距离与MRISA+TSA算法的相对偏差率（Relative Deviation Percentage，RDP），表中简称为RDP(1)，如表3所示。其中，RDP(1)=（DisMRISA+TSA-Dis所选算法）/Dis所选算法。

表3的实验结果显示：1）SPLITABU 和 ISA+TSA的行驶里程RDP除了实例“v11-120-7”外其余的都小于6%；这表明MRISA+TSA对除了实例“v11-120-7”外那些具有物理位置分散分布（如图1所示，红色为车场）的实例可以获得近优解；2）NSA+TSA和 MRISA+TSA的行驶里程RDP(1)均小于0，说明MRISA+TSA的行驶里程小于NSA+TSA的行驶里程，MRISA是必要的，可行的和有效的；4）MRISA+TSA的计算时间比SPLITABU低的多，最大的计算时间小于15s。

表3 案例2的实验结果

图1 客户点围绕车场分散分布

图2 客户点围绕车场集群分布

但是，表3显示SPLITABU在实例“v11-120-7”的行驶里程的RDP(1)很大，为20.9%。这说明MRISA算法在这个实例上无效。实例“v11-120-7”的地理分布特征是所有的点都成集群形状分布在车场周围，如图2(a)所示“v11-120-7”。为了适应这个特征，我们采用了“先聚群再扫描”的策略。首先，采用“Max-Min dis”[18]方法对客户聚群；然后再对每个聚群采用MRISA +TSA，即三阶段方法“Max-min dis”+MRISA+TSA。

根据“Max-Min dis”方法的原则，首先，按照最远距离（Maximum distance）原则，选择相距最远的点作为聚群中心，使得初始数据集的分割效率较高。然后，按照最近距离（Minimum distance）原则，将所有距离最近的点就近归入聚群组[18]，如图2(a)所示，红色为车场，深红色的点为各聚群中心；最左边两个聚群连在一起，为了区别、其中一个聚群用绿色点表示。如果每个聚群的总需求量≤α×Q（α>1正整数），MRISA +TSA可以在各聚类中执行；如果某聚类的总需求量>α×Q（α>1正整数），通过“推出”、“拉入”操作调整各聚群的需求量，使各聚群的总需求量≤α×Q（α>1正整数），然后再在各聚类中执行MRISA +TSA。

算法“Max-min dis”+MRISA+TSA在实例“v11-120-7”上的执行结果见“Max-min dis”+MRISA+TSA列的“v11-120-7”行（最右列黄色）。结果表明采用算法“Max-min dis”+MRISA+TSA后行驶里程下降了。行驶里程与SPLITABU和 NSA+TSA行驶里程相比的RDP；2）分别为6.9%和-17.6%，分别比RDP(1)下降了约14%and 10.8%；而采用“Max-min dis”+MRISA+TSA算法后的行驶里程比MRISA+TSA算法也下降了，RDP(2)为-11.6%。其中，RDP(2)=（Dis“Max-mindis”+MRISA+TSA-Dis所选算法）/Dis所选算法。

为了进一步验证三阶段算法在具有与实例“v11-120-7”类似地理分布特征的实例上的执行效果，本文采用“Max-min dis”+MRISA+TSA算法在实例“v12-100-10”（如图2(b)所示，红色为车场）上执行（SPLITABU[3]无执行结果）。执行结果表明采用“Max-min dis”+MRISA+TSA算法后的行驶里程下降了，NSA+TSA与MRISA+TSA的RDP(2)分别为-20.1%和-10.1%，NSA+TSA的RDP(2)比RDP(1)下降了8.9%。

实验结果表明三阶段算法“Max-min dis”+MRISA+TSA对于客户点围绕车场集群分布的实例比两阶段的算法MRISA+TSA有效的多。

4 结论

针对SDVRP，本文提出了一种基于构造启发式的两阶段算法。第一阶段，采用多重启动迭代策略在逆时针和顺时针方向从每点开始扫描客户域。根据车辆容量将客户域划分为子域。负载率LF和TC用于微调分区、拆分点和拆分负载。第二阶段，TSA用于优化每个子域中的路径，以实现最小的总运输距离。

数值实验是在CVRPLIB基准数据集上进行的。计算结果表明，MRISA多重启动迭代策略是必要的，并且该算法在大多数测试数据集实例中为SDVRP提供了可行有效的解决方案。所提出的算法在数据集1的11个实例中有7个获得近似最优解（RDP<5%），数据集2的6个实例中有5个获得近似最优解（RDP<6%）。另外，数据集1和2计算所耗的最大时间分别是3s和15s，他们大大的低于所评价的其他算法。

进一步实验表明：两阶段MRISA+TSA方法对客户地理位置分散分布的实例是有效的；而三阶段的“Maxmin dis”+MRISA+TSA方法则对客户地理位置集群分布的实例更加有效。