防爆油箱爆炸冲击响应数值模拟方法研究
2019-10-22王显会周云波皮大伟
曾 爱,王显会,周云波,皮大伟
(南京理工大学 机械工程学院, 南京 210094)
近年来随着我国综合国力逐步提高,我国参与国际维和行动和反恐任务次数增加,使我国维和人员和车身的安全受到严重威胁。燃油箱作为车辆底部关键零部件,其不仅为动力装置输送燃油,还严重影响车底部防护性。因为在地雷或简易爆炸装置爆炸冲击作用下,燃油箱会受到强力的冲击,由于其厚度薄变形严重甚至出现开裂,有时爆炸后的高速产物以及泥土穿透油箱,加上燃油强烈振动使油箱开裂更严重,这不仅影响油箱储存燃油能力,而且燃油泄漏起火甚至爆炸对车身和乘员造成二次伤害,这严重威胁车身和乘员的安全,但是目前对车辆底部防护仿真研究时,受限于模型规模和计算时间的要求,燃油箱的燃油的处理方法是将其质量等量附加在油箱上。该方法能满足前舱结构设计的精度要求,但忽略油液晃动以及燃油泄漏引起火灾甚至爆炸爆炸等问题。因此研究在爆炸冲击作用下燃油箱的损伤特性,提高燃油箱抗爆炸冲击能力和军用车辆底部防护能力具有重要的意义。
目前,军用车辆底部及其零部件的地雷防护研究方法主要有试验法和数值模拟法。爆炸试验法对关注信息获得具有准确性,也是最直接得到目标信息的有效方法,但操作时间比较长、耗费人力大、所用经费较多。数值模拟能够模拟实际情况,并且运作周期短、效率高、重复性强等优点。在爆炸领域的仿真算法多数用ALE算法,其计算精度高,是被公认最成熟的算法。彭兵[1]用ALE算法分析靶板在爆炸冲击作用下的动态响应,并用理论计算结果对比了仿真结果,验证了ALE算法的准确性。李利莎[2]通过LS-DYNA软件分别用拉格朗日算法、ALE算法和SPH算法模拟炸药爆轰及混泥土破坏全过程,比较了3种算法的优缺点。国内外许多相关研究者通过数值模拟技术对军用车辆及其零部件防护做了大量的研究。如王显会[3]采用LS-DYNA软件研究某军用车燃油箱在爆炸冲击波作用下的防护强度,提出以油箱承受的TNT当量为表征参数作为爆炸冲击防护强度,并对油箱进行改进提高了其防护能力。郑虔智[4]通过Pam-crash软件利用SPH算法模拟水箱晃动,并用试验验证SPH的可行性和有效性。Anderson[5]通过数值模拟得出船体结构在爆炸冲击作用下变形和破坏形式。刘雄健[6]采用SPH方法模拟无人机油箱抗冲击过程,与拉格朗日-欧拉算法比较发现SPH法在流固耦合问题上是适用的。用SPH粒子模拟水在水槽中的纵摇情况,并用实验进行验证,得出了SPH方法模拟液体晃动具有真实性的结论。冷飞[7]将SPH方法运用到飞机油箱晃动问题上,比较准确地模拟燃油晃动等非线性现象。唐浩[8]用SPH方法研究分析导弹油箱燃油晃动对油箱结构的影响,计算得到了油液重心变化曲线以及油液与油箱之间的相互作用力。
爆炸冲击作用下油箱动态响应问题涉及多相流之间的相互耦合问题,为了避免冗余耦合问题和提高计算效率,传统的方法是将油液的质量等量赋给油箱即等效配重法,这虽然满足结构设计精度要求,但忽略油液晃动对结构影响。用SPH粒子模拟油液,ALE算法模拟爆炸,这即避免了冗余流固耦合问题,也有效结合SPH和ALE优点,保证计算结果的准确性。通过比较SPH粒子模拟燃油和等效配重法加载燃油两种加载方式,比较燃油箱在爆炸冲击波作用下变形及应力分布特征的差异性,为后续车辆底部防护研究提供一定的参考。
1 数值算法理论
1.1 ALE理论
任意拉格朗日法(Arbitrary Lagrange-Euler,ALE)是把不可压缩材料结构用拉格朗日网格划分,把可压缩流体材料(如空气,水)用欧拉网格划分,它们之间用多物质流固耦合进行接触。这结合了拉格朗日算法和欧拉算法的优点,既避免了拉格朗日算法在网格大变形中出现畸变问题,也解决了欧拉算法中空间网格不移动的缺点,能够有效模拟流体与固体的耦合问题, ALE描述物质物理量表达式:
其中:f为物质点物理参数,υi为物质i质点的速度,wi为参考点ξ的速度,当参考点速度为0时,表达式为
空间网格固定不动,材料网格运动,即为欧拉网格;当参考点速度等于物质的流速时,表达式为
空间网格与材料网格不存在相对运动,流体网格为拉格朗日网格;当参考点速度与流体速度不相等时,空间网格与材料网格可以一起运动,并且材料网格可以在空间网格一定区域内流动。
ALE算法能有效模拟泥土、空气和爆炸冲击波整个流动过程,所以计算精度高,可靠性好,是目前在爆炸仿真中公认最有效的仿真算法。
1.2 SPH基本理论
高速大变形材料一般采用ALE网格,本文的炸药、空气和土壤都采用ALE网格,其计算精度高但计算时间相对较长。油液用ALE模拟虽然保证了计算精度,但出现多种耦合,计算时间大大加长,为了保证计算精度和减少计算时间,避免冗余耦合问题,油液用SPH模拟。
SPH方法最早由Lucy[10]和Gingold[11]等人提出的,主要用于天体物理学,后来经过RANDLES P W等[12]不断完善,在大变形流体领域得到广泛应用。SPH是将连续性研究对象划分成一系列有质量的粒子,通过插值法解决连续的物理问题。由于其无网格并采用核函数近似,不存在网格畸变和网格质量不合格问题。SPH通过核函数近似法和粒子近似法得到连续函数积分表达式:
其中:x为粒子的矢量坐标,K为x的积分体积,x-x′为两个光滑粒子之间的距离,W(x-x′)为插值核函数。一般用光滑函数W(x-x′,h)代替插值核函数W(x-x′),所以粒子函数积分表达式:

其中:h为粒子光滑长度,光滑长度与计算精度和计算时间有关,随着粒子之间距离增大而增大,随着粒子距离减小而减小。
2 数值计算模型
2.1 有限元模型的建立
油箱总成包括油箱、安装支架和油箱绑带,忽略油箱内部结构以及箱体之间焊缝失效,有限元模型如图1所示。箱体基本尺寸为:长1 044 mm,宽485 mm,高320 mm,厚2 mm;油箱支架厚度2.5 mm。油箱网格类型为壳单元,网格基本尺寸10 mm,划分2 220个单元。为了准确模拟材料在大的应变、高应变率和高温度下的力学性能,油箱材料模型采用Johnson-Cook模型材料,密度7.85 g/cm3、弹性模量210 GPa、泊松比0.3、屈服极限0.55 GPa。
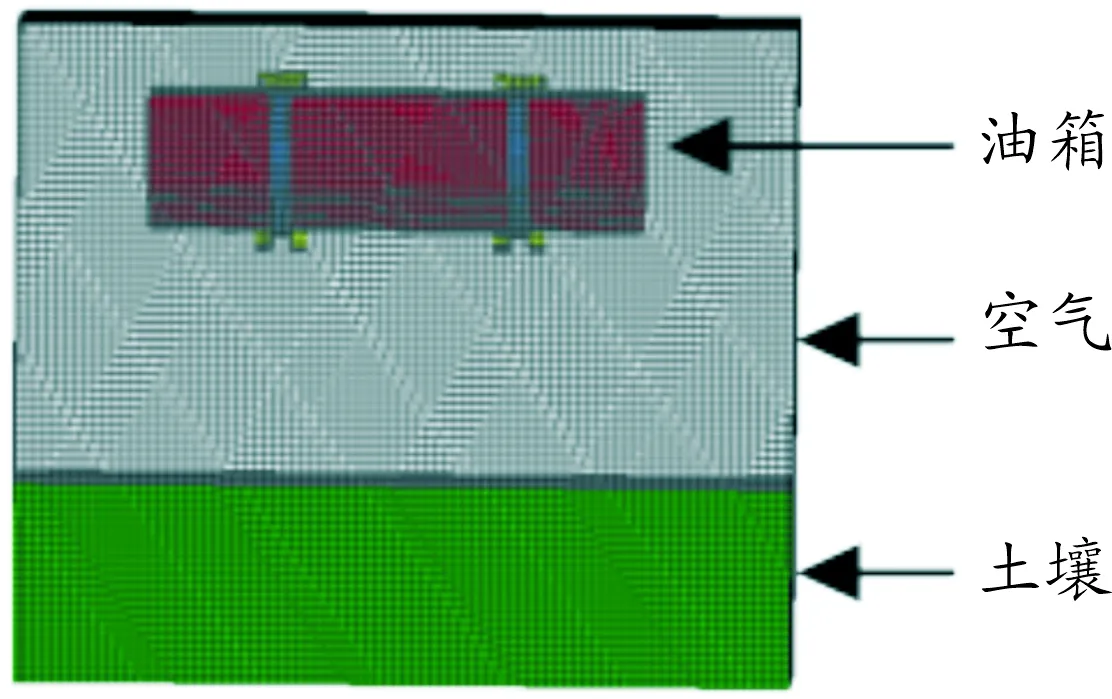
图1 有限元模型
土壤网格基本尺寸:长1 640 mmm,宽1 200 mm,高450 mm,网格类型为体网格,基本尺寸20 mm,总单元数为113 160个,土壤与空气通过共节点连接。空气域覆盖整个油箱,其基本尺寸为:长1 640 mm,宽1 200 mm,高1 080 mm,网格类型为体网格,基本尺寸20 mm,网格数位557 282。其材料用空材料模型和线性多项式状态方程,状态方程为
p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E
其中:P气体压力,Ci(i=1、2、3、4、5、6)为多项式方程系数,E为单位体积初始内能。C0=-0.1;C1=C2=C3=C6=0;C4=C5=0.4;E0=0.253 mJ/mm3;V0=1。
为了准确描述炸药爆炸之后的物理状态,引入了爆轰产物气体状态方程和爆炸源控制方程,能精确计算爆炸产物体积、压力、密度、爆速和能量的关系。其中爆炸产物气体状态方程采用由Jones、Wilkins和Lee经过大量试验拟合的出来的JWL方程。其表达式为:
JWL方程满足C-J条件的等熵方程:
其中:A=3.72 MPa;B=0.003 MPa;R1=4.15;R2=0.9;ω=0.35,P为炸药的压力,E为单位体积的爆炸能量即初始比内能为0.007 23 mJ/mm3,Vc为炸药爆炸之后产物比容与初始比容的比值。根据文献[5]油箱对爆炸冲击波的防护强度在160 g左右,取炸药重量140.5 g。
油液分别有SPH和等效配重两种加载方式。SPH加载方式如图2(a)所示,光滑粒子长度为1.2,最小长度比例因子0.2,最大长度比例因子2。等效配重法是将油液质量直接赋给油箱即将油液质量平均赋在油箱每个节点上,如图2(b)所示。
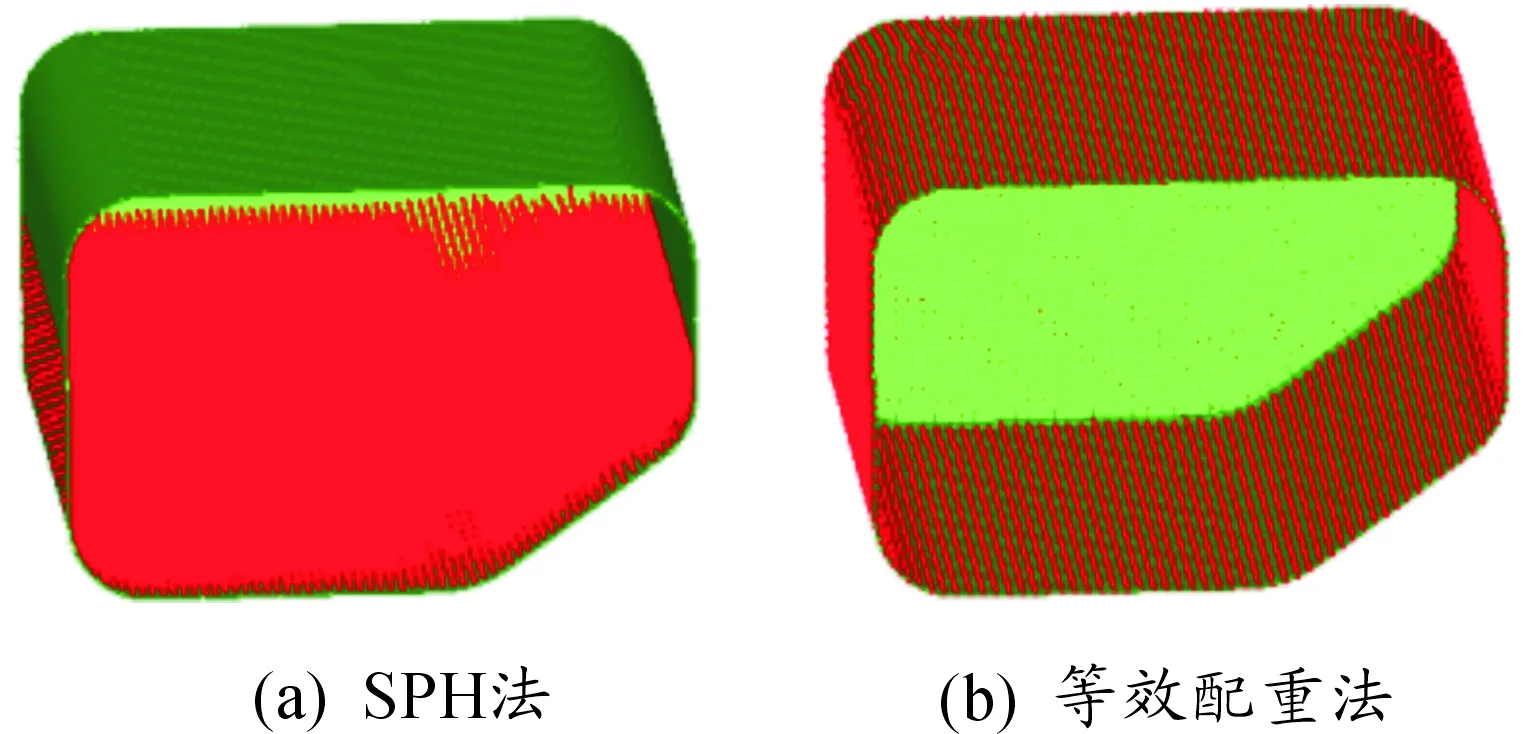
图2 两种加载方式
2.2 边界条件与接触设置
根据北约军用车辆防护等级试验要求炸药埋在土壤里面,离地高度为10 cm。车离地间隙为58.7 cm,所以炸药离油箱高度为68.7 cm且炸药位于油箱正下方。在支架与车连接部位的螺栓孔进行6自由度约束。油箱、支架和绑带之间采用面面接触(*CONTACT_SURFACE_TO_SURFACE)。炸药、土壤、空气和油箱总成之间用多物质流固耦合(*CONSTRAINED_LAGRANGE_IN_SOLID)。光滑粒子与油箱之间用点面接触(*CONTACT_AUTOMATIC_NODES_TO_SURFACE)。
为了比较SPH粒子加载燃油和等效配重加载燃油的差异性以及油箱损伤特性分布规律,分别取不同体积分数的燃油和对应的燃油质量,如表1所示。

表1 燃油体积分数和质量
3 数值计算结果分析
3.1 油箱和油液的变化
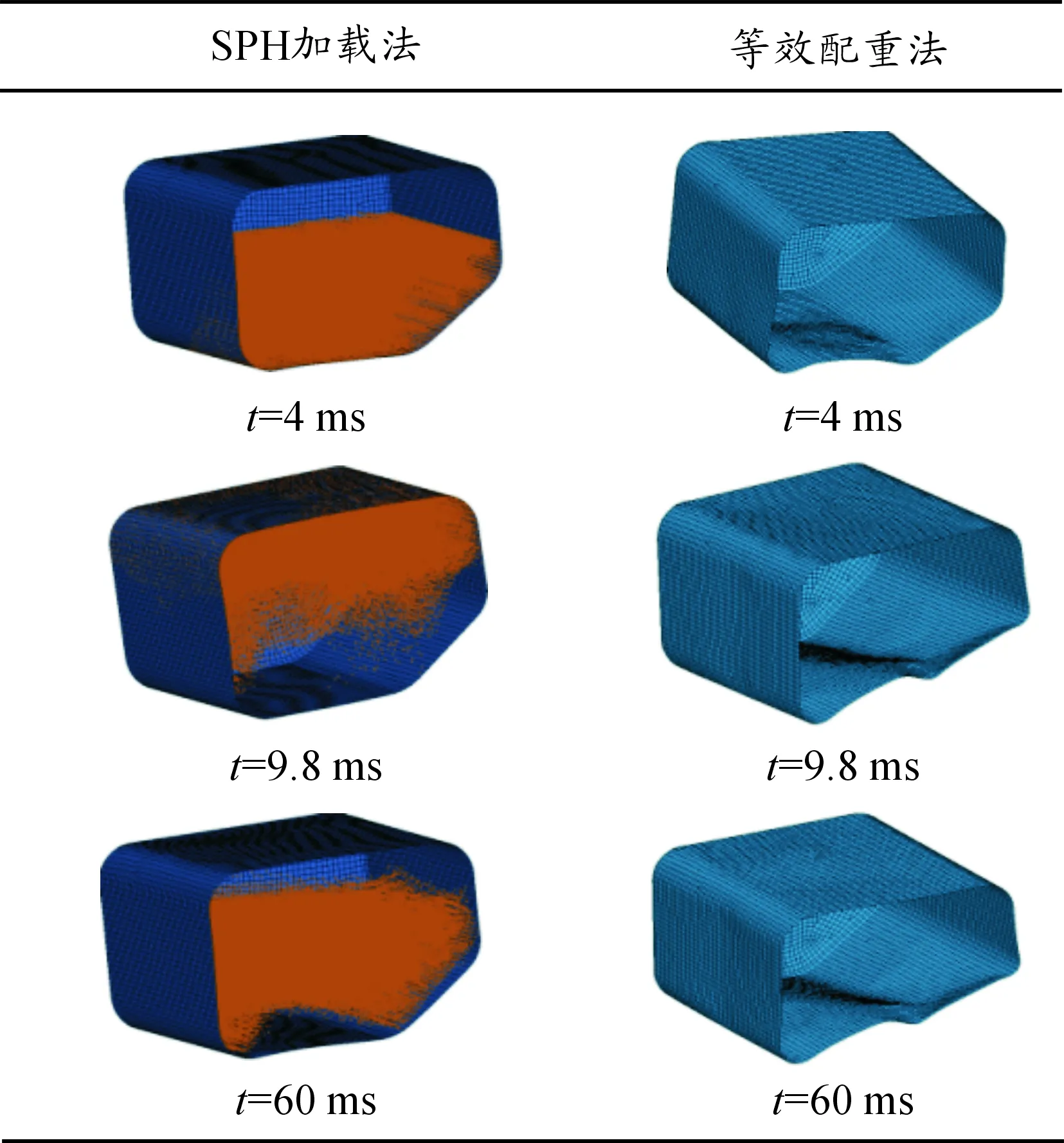
爆炸冲击作用下两种加载方式的油箱油液变化如表2所示。在4 ms时刻爆炸冲击波到达油箱底部,SPH法油箱底部几乎未变形,油液轻微地波动,4~9.8 ms油液向上运动且在9.8 ms时刻大部分油液脱离油箱底部到达油箱中间,油箱底部中间向上凸起,在60 ms时刻大部分油液接触油箱上部分,油箱底部向上凸起减小。SPH方法比较真实地模拟油液晃动情况。等效配重法油箱在4 ms时刻油箱底部向上凸起明显,在9.8 ms时刻凸起最严重,在60 ms底部凸起减小。
表2 油箱和燃油变化
为准确地比较油箱垂向变形情况,在油箱上下表面中间部位取两个点,测量两点垂向距离随时间变化,如图3所示。SPH载法油箱上下表面距离在9.8 ms左右最大,底部凸起最严重,在10~20 ms距离逐渐减小,20 ms后由于油液对油箱冲击作用,曲线上下波动。等效配重法油箱上下表面距离变化情况与SPH相似,但距离明显大于SPH法。
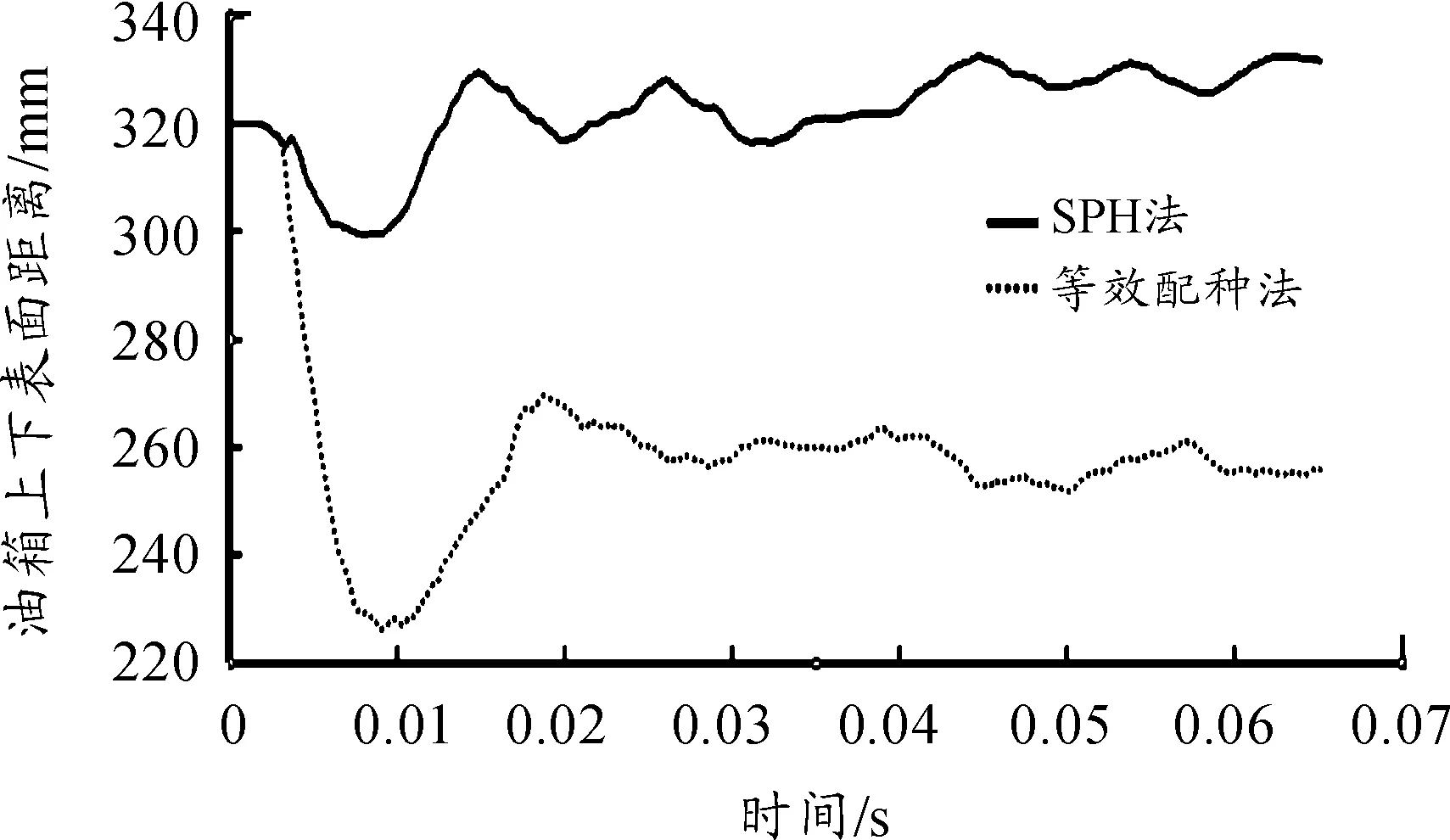
图3 油箱上下表面距离
3.2 油箱损伤结果分析
车辆油箱防护基本要求是其不能出现裂纹,应力要小于材料的屈服应力。在数值模拟中分别得到了两种不同加载方式油箱在9.8 ms时刻应力云图。如表3所示:SPH法油箱高应力分布区域较少,绝大部分区域处于低应力阶段,大变形区域在油箱侧面,底部变形较小。等效配重法高应力分布区域较多,主要集中在油箱底部中间,大变形区域在其底部中心处,其底部严重向上凸起。
两种加载方式油箱最大应力值与油液容量变化规律如图4所示。SPH加载油液方法油箱最大应力随着油液容量增加先增后减趋势,容量在60%左右时油箱最大应力值最大,油箱损伤最严重。等效配重法油箱最大应力随着油液容量增加几乎平稳不变,增加油箱质量对油箱防护性没有大的影响且等效配重法油箱损伤比SPH法更严重。
两种加载方式油箱最大变形量与油液容量变化规律如图5所示。SPH法油箱变形量较小,随着油液增加,油箱变形量有着先增后减趋势,整个曲线波动不大。在60%油液的油箱最大变形最大。等效配重法随着油液增加,油箱变形量最值也是平稳不变的趋势,增加油箱质量对油箱变形没有太大的影响,但是其变形量远大于SPH方法
表3 应力位移云图
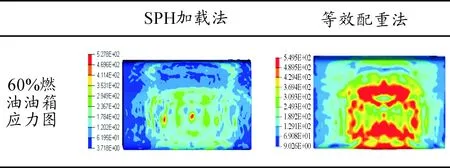
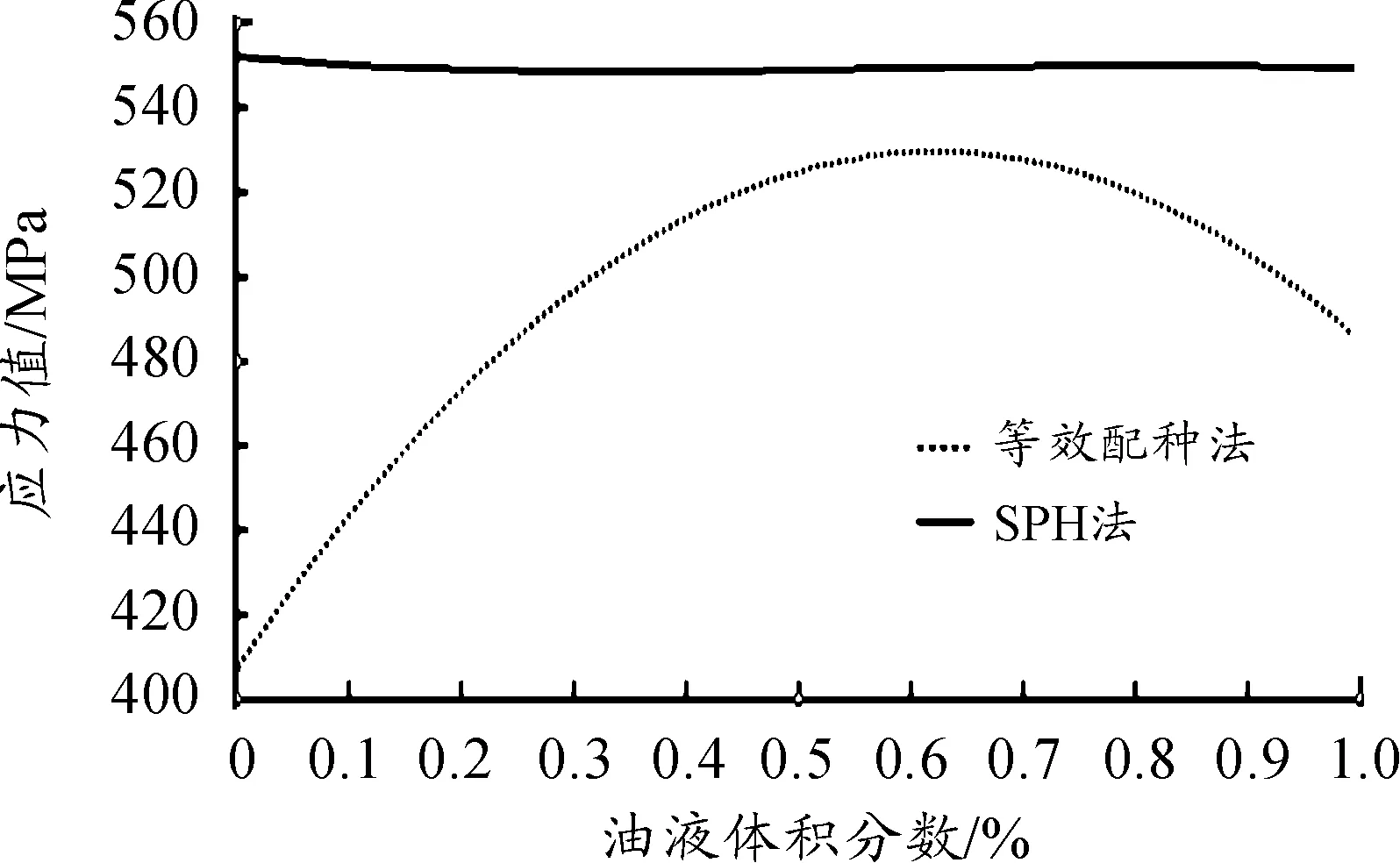
图4 油箱最值应力曲线
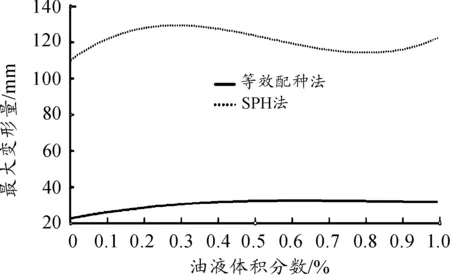
图5 油箱变形量关系曲线
为研究两种加载法的油箱损伤特性,取60%燃油的油箱分析其能量变化趋势。图6为两种加载方式油箱的内能变化曲线。两种方法油箱都在在9.8 ms时刻出现峰值,与油箱出现的最大应力值和变形量时间点一致。等效配重法油箱内能在峰值之后趋向平稳,最大值为2.618 kJ。SPH法油箱的内能在峰值之后减小最终平稳不变,最大值为0.167 kJ,远小于等效配重法油箱内能。油箱和燃油吸收内能曲线如图7所示,在初始阶段由于油箱首先与爆炸冲击波接触,油箱吸收能量大于油液,在9.8 ms后由于油液吸收能量增大,对油箱的冲击力增大,使油箱变形量减小。所以SPH法油箱损伤较小是由于油液吸收大部分能量,油液晃动冲击油箱使其变形量远小等效配重法油箱。

图6 油箱内能曲线
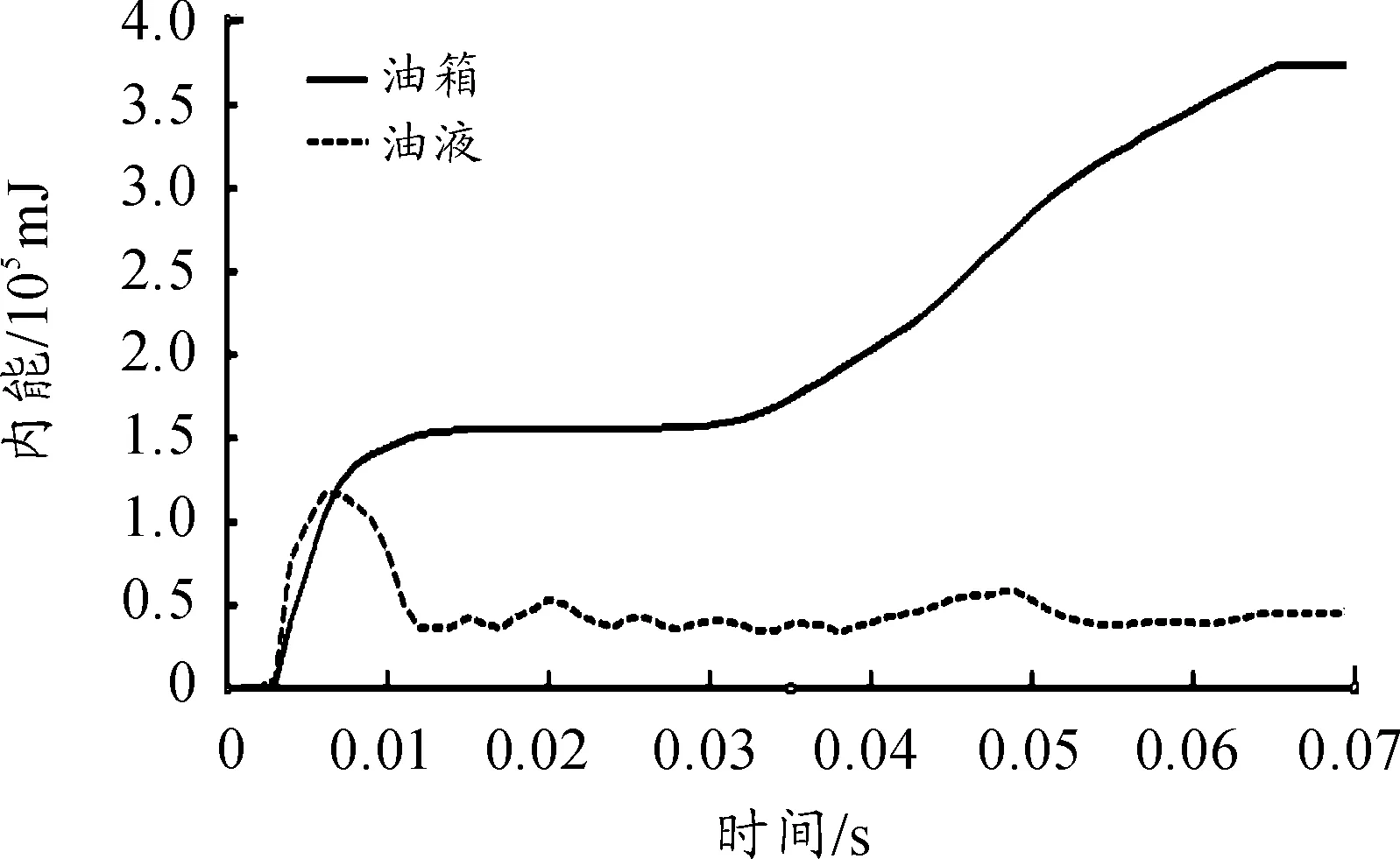
图7 油箱和燃油内能曲线
4 结论
1) SPH技术模拟燃油法能够有效模拟油液运动情况,并且油液对油箱的结构响应影响很大。等效配重法赋给油箱质量几乎不影响油箱损伤情况。
2) SPH技术模拟燃油法增加油液容量,油箱的最大应力值和最大变形量值都先增后减,在60%左右油液容量时油箱受损最严重。
