基于伪寿命数据的数控机床可靠性评估

马仕川 罗静 杨立波

摘 要：针对传统数控机床性能研究需要大量退化数据和标准的退化模型参数的问题，研究基于伪寿命数据的数控机床可靠性评估方法。首先建立机床数据的线性模型，并通过显著性检验检验模型的合理性，然后在选定失效阈值的情况下得到机床的伪寿命数据，并以此为全样本数据利用minitab进行寿命分布模型的优选，最终得到机床的可靠性函数，完成数控机床的可靠性评价。

关键词：伪寿命数据;数控机床;分布模型;可靠性评价

中图分类号：TP114文献标识码：A

数控机床的故障是各零部件在运行过程中受外部综合条件发生断裂、锈蚀、磨损或变形等[1]而造成的。目前数控机床朝着多性能、长寿命方向发展，传统试验难以在有效时间内得到足够的寿命数据来验证数控机床性能退化失效的过程，造成试验设备、试件、材料等的浪费;另外，传统方法对退化模型的参数要求比较严格，在实际测试中很多设备采集的数据并不理想，使得退化模型无法识别，影响可靠性评估工作的开展。本文以机床性能检测数据为基础，通过建立线性回归模型，得到数控机床的伪寿命数据，研究基于伪寿命数据的数控机床可靠性评估方法，为数控机床可靠性工作的开展打下坚实的基础。[2]

1 线性模型建立

在试验过程中，采用观察点（xi，yi）（i=1，2，…，n）对试验样本进行记录，当两个数据存在因果关系时，可以运用函数表达式将将关系表现出来，然后利用离差杠杆图观察数据拟合的合理性。

2 回归方程显著性检验

3 基于伪寿命数据的可靠性评估

数控机床在实际运行过程中，存在众多精度需要考核，大致分为静态精度和加工动态精度。[4]为研究方便起见，通常是以数控机床的静态精度为研究对象，加工精度受多种因素影响而不易控制，无法进行数据的采集。定位精度是数控机床在验收时和实际工程中重要的考核指标，由于经费和试验时间的限制，文中数据来源于文献[6]，检测样本1的数据如下表所示，本文主要研究方法，示例性说明基于伪寿命数据的数控机床可靠性评估方法。首先拟合回归曲线，并进行显著性检验;然后确定失效阈值，求解数控机床的伪寿命数据;最后进行寿命数据分布模型识别，得到相关可靠性函数。具体步骤如下：

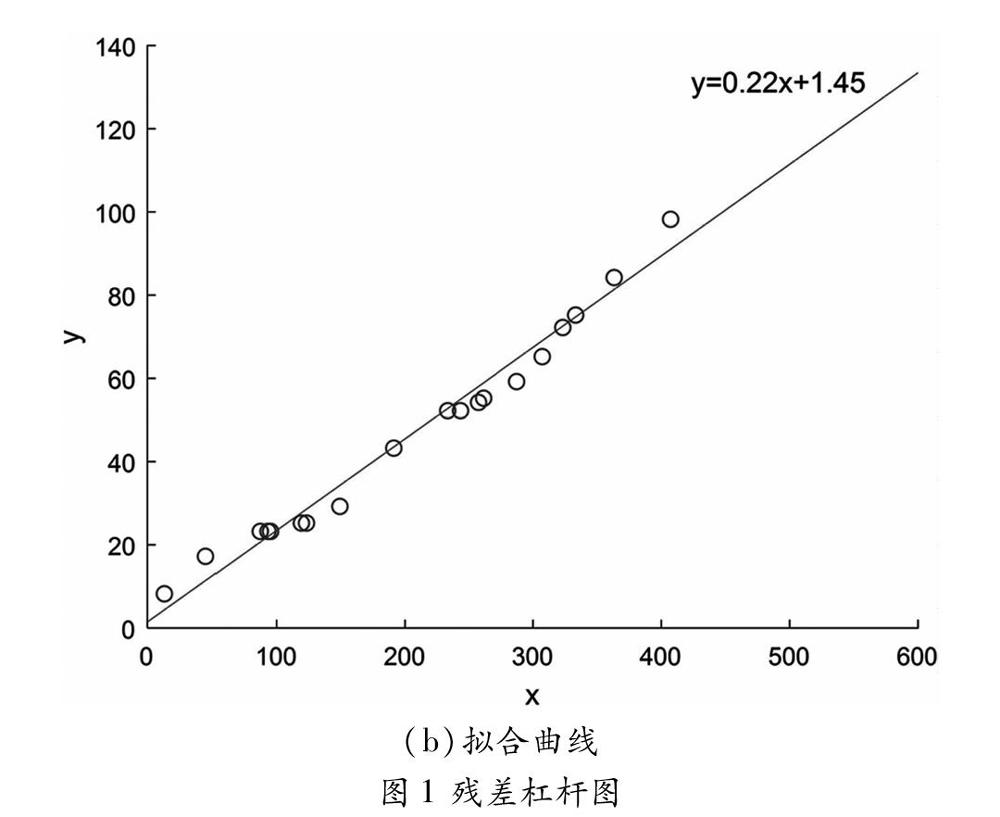
（1）线性关系求解：以样本机床1为例，计算得到x、y的回归方程为y=0.22x+1.45。为了分析回归模型与原数据点之间的偏差，作出各个数据回归点的残差杠杆图，如图1（a）所示。

（a）残差杠杆图

（b）拟合曲线

由图1（a）的杠杆图得出，除最后一个数据的残差置信区间没包含零点外其余都在，说明回归模型y=0.22x+1.45较好的拟合了原始数据，其拟合效果如图1（b）所示。查阅文献[4]中的附表4，选定显著水平α=0.1，F1-αdfR，dfE=3.01，计算样本1的F值。F=3.56>F1-α，说明x与y的显著性明显。采用相同的方法对文献[6]其他测试机床的数据进行处理，求得各测试机床的线性关系。

（2）伪寿命数据计算：结合参考文献中的失效阈值，利用拟合的回归关系可以得到各个数控机床的伪失效寿命，分别为1357，1300，1860，1071，2285（单位/h）。

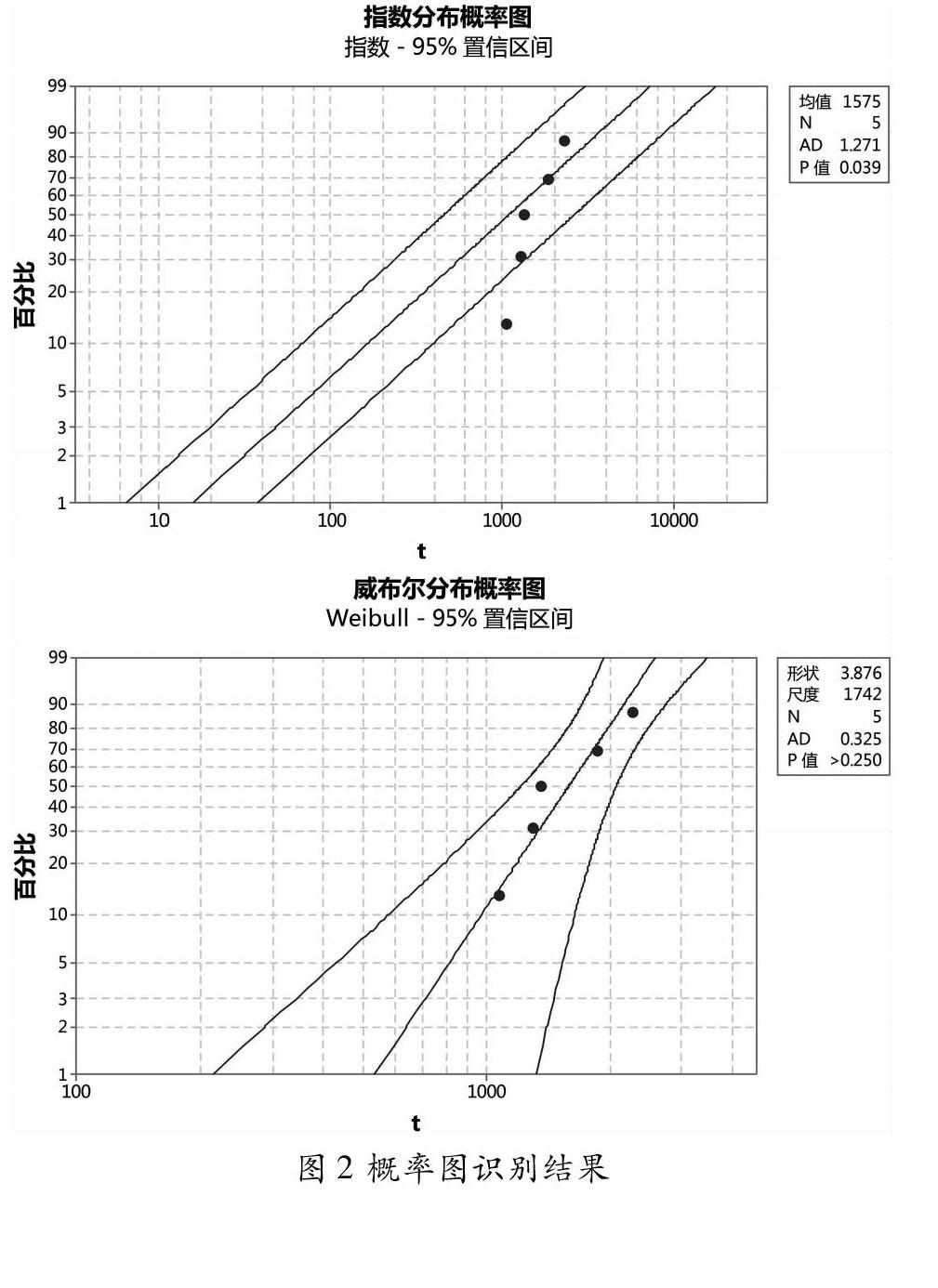
（3）寿命分布模型识别：使用minitab软件的概率图方法对伪失效寿命数据渐进性模型优选，主要分布模型为威布尔和指数分布，因此分别对其进行概率图检验，如图2所示。

（4）可靠性函数确定：经过步骤（3）的检验，可以将步骤（2）中的伪寿命数据作为数控机床的完全样本数据，根据威布尔分布特点，可以求得数控机床的失效概率密度函数ft、可靠性函数Rt以及MTBF的点估计值等。

文献[6]中主要研究基于主机厂与用户厂性能检测数据的可靠性评估方法，实现性能数据的协同分析和动态更新，[5]该方法的基本框架需要大量的性能检测数据作为评价基础，许多主机厂和机床厂缺乏这方面的数据，导致评价工作无法开展。本文从单一性能退化指标出发，构造数控机床的简单线性回归模型，得到其伪寿命数据，并运用minitab软件实现寿命数据分布模型的识别，确定相关可靠性函数表达式，最终得到该型数控机床的平均无故障工作时间为1576h。

4 结论

本文利用数控机床性能退化数据，首先建立了线性回归方程，并通过显著性检验说明了回归方程的显著效果，利用残差杠杆图说明回归方程的合理性;然后选定失效阈值外推数控机床的伪寿命数据并以此为完全样本，通过软件完成模型的优选，从而得到数控机床的相关函数;最后由威布尔分布的性质得到数控机床的平均无故障工作時间为1576h。本文的可靠性评估方法不仅减少了数据处理的计算量，还降低了评估过程对性能退化数据的需求量，具有较大的工程应用价值。

参考文献：

[1]金光.基于退化的可靠性技术[M].国防工业出版社，2014.

[2]A.C.普罗尼柯夫.数控机床的精度与可靠性[M].北京：机械工业出版社，1987.

[3]马义中，欧阳林寒.现代质量工程[M].北京：科学出版社，2018.

[4]李继中.改善数控机床精度的方法探索与分析[J].工具技术，2012，46（01）：48-52.

[5]彭卫文.重型数控机床可靠性建模与评估技术研究[D].电子科技大学，2016.