基于非线性算法的制造资源多目标优化配置模型研究

2019-10-21杨培义张天彤张慧勤

汽车世界·车辆工程技术（中） 2019年6期

杨培义张天彤张慧勤

摘要：为优化配置多目标制造资源，分析了制造资源生产能力的约束和资源供应状态的约束;用非线性动态规划算法，按照经济效益最先性原则，构建了一套制造资源多目标优化配置模型;以G试验器材制造公司为例，结合自编的MATLAB算法求解，然后提出计算机辅助算法，运用EXCEL进行检验;实证表明，在生产要素约束条件下，实现了多目标资源优化配置，完成了生产定制，满足了顾客需求;验证了构建的非线性多目标资源优化配置模型可行性和自编程序的正确性，并且该模型难度适中、易于操作。由此表明，该模型可为多目标制造资源优化提供实践指导和理论依据。

关键词：非线性算法;动态规划法;制造资源;资源优化;MATLAB算法

0 引言

多目标企业制造资源主要包括人力、厂房、设备、工艺技术、软件、物料、信息、服务、财务等资源，简称物质流、信息流、资金流，有广义概念和狭义概念之分，广义概念是指原材料进厂到成品出厂整个生产周期的物质流、价值流、信息流所涉及的生产要素，也包括研发设计、生产制造、销售交付等相关过程涉及的要素。狭义概念是指加工制造、生产装配一个零部件所需要的物质元素，主要包括工装等。多目标制造资源优化配置Manufacturing Resources Optimal Allocation （MROA），是通过一定的调度方式把有限的人财物等生产要素资源合理分配到企业的各个生产单元中，以实现资源最佳利用，获取最佳效益。随着时代经济的发展，智能产品、复杂产品、高尖端产品不断面世，新的制造资源优化模型和方法也不断出现，很多学者针对不同环境、不同目的展开广泛研究，已从面向单一信息化模式发展到面向不同信息化应用模式，支持产品全生命周期应用[1-2]。如张中伟[3]等人针对如何优化设计工艺和机械加工制造资源提出非线性工艺规划资源优化配置模型，并运用遗传算法求解;蓝伯雄[4]等人针对传统MRP逻辑存在固有缺陷，提出一种基于滚动计划的动态企业资源优化模型。葛家家[5]等人针对服务型企业的特点和特征，提出以资源和时间作为决策变量构建项目资源优化模型，包北方[6]等人为实现产品定制协同生产，提出产品定制协同MROA的双层规划求解方案。蒋南云[7]等人为寻求出厂检验环节的最优运行策略，应用Jackson排队网络理论，研究了出厂检验环节检验设备、运输车辆及抽检人员的资源配置优化问题。付银环[8]、李奥典[9]等人提出基于两阶段随机规划法建模应用于灌区水资源优化配置。本文主要针对制造系统在人财物等生产要素有限资源约束下，引入非线性动态规划算法，建立一套动态监控机制，以实现人财物等资源优化配置。动态规划是美国数学家贝尔曼等人提出的解决多目标多阶段决策过程优化的一种方法[10]，在工业、服务业、交通运输、现代物流等领域得到了廣泛应用，并且获得了显著的效果[11-15]。

1 制造资源优化模型形成方案

制造资源优化配置（Manufacturing Resources Optimal Allocation，MROA）不仅要考虑生产能力资源约束，还要考虑资源供应状态的约束。生产能力资源一般指与研发设计、生产制造和交付销售相关的三大流，即物质流、信息流、资金流。它是支撑现代制造业生产规模和产能的基本要素，与市场需求有密切关系;当市场需求上升时，则需要考虑如何增加制造资源供应，以满足市场需求的增长;当需求不足时，则需要考虑如何缩小资源规模，避免生产能力过剩，减少三大流损失。资源供应的状态主要反映产品在制造过程中制造资源使用的状况，是生产能资源重要的组成部分，此外，生产能资源与其存在线性关系，生产能力资源会随着资源供应状态的变化而变化，而资源供应状态恰好反映其在特定时间内是否可用[16-17]。本文主要针对生产能力在各种资源约束下，引入非线性算法，建立一套动态监控机制，以实现多目标人财物等MROA，如图1所示，多目标MROA产生的过程，第一层为资源池，是企业在生产过程中需要调配的各种资源，其中人力资源、物料资源、设备资源等组成物质流，和财务相关的资源组成资金流，技术资源、信息资源、软件资源等组成信息流;第二层为目标层，用于描述优化资源配置的多目标性;第三层与第四层分别为方法层和决策层，是确定最佳目标，采用的方法和策略;第五层为方案层，是经过第四层定性定量决策筛选、评估所形成的多个优化方案;第六层为优化模型备选层，可针对不同备选的优化模型，采用合适的算法和相关软件，求解模型;第七层为最佳方案层，经过相应算法验证求解，筛选出最佳资源优化配置模型。本文将生产能力资源视作制造资源的静态属性，重点研究资源受限对非线性动态规划算法设计的生产计划能力的影响，以G绿色能源公司为例，按照顾客生产定制要求，运用非线性算法构建多目标资源优化配置模型。

2 非线性算法构建优化模型

2.1 基本思想

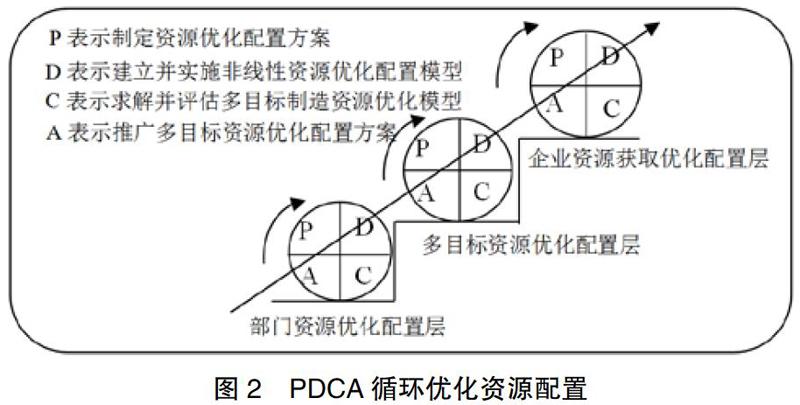
在本文采用的非线性算法是指动态规划法，动态规划算法的优势在于利用最优化原理给出最优值函数的递推关系式和边界条件，首先将多目标问题划分为若干个相互联系的阶段，然后选取状态变量和决策变量，写出状态转移方程及定义最优值函数。从而把多目标多层次问题转为若干个同类型的子问题，再逐个求解。PDCA循环优化资源配置如图2所示，把多目标资源优化配置看成相互联系的多阶段问题，赋予其状态变量和决策变量，然后运用非线性动态规划算法建模，按照PDCA循环爬楼梯上升式的资源优化，每转动一周，即进行一轮优化方法，表示制造资源优化配置一层。

2.2 动态规划建模

（1）将多目标问题看成一个有机整体，根据需要划分为若干个子问题阶段;

（2）根据实际情况，选取状态变量;

（3）根据多目标问题给定的前提条件，定义决策变量并确定每个子问题决策集合;

（4）写出问题状态转移方程;

（5）确定各个子问题的阶段指标，列出最优策略基本方程并求解。

2.3 动态规划求解

（1）按照多目标问题的时空特征，把其分为若干个子问题并编号;

（2）确定各个子问题的各种客观情况，用不同状态表示并且状态的选择要满足无后效性，状态变量和状态集合分别用和表示;

（3）确定决策变量和允许决策集合;

（4）确定阶段指标;

（5）确定问题状态转移方程;

（6）确定求解逻辑顺序，并给出相应的递推公式或方程，包括边界条件;

（7）实施迭代求解。

2.4 动态规划的数学模型

从多目标资源配置问题中，求解并递推非线性动态规划基本方程：

其中目标函数;阶段指标;称为边界条件。

3 案例分析

G为试验器材制造公司，主要生产冷热冲击试验机，产品规格、功率、型号按照顾客要求来确定，以节约制造资源，保证产品和生态质量为核心，与顾客订立生产定制合同，在5个月内生产台数为10的倍数的冷热冲击试验机，假如G公司每月产量上限为100台冷热冲击试验机，此产品可存储，库存费用为每台200元/月，月需求量及每台制造成本见表1。现在要求在两种情况下确定月出产量：1月初无存货和1月初有20台库存;要求既能满足顾客每月生产定制的合同需求量，又能使冷热冲击试验机生产资源成本和库存费用达到最小。

3.1 分析问题

本案例是一个典型的非线性规划多目标生产定制问题，这里可把这个问题的解决动态地视为各个月先后做出决策的过程——多目标的决策过程，在每月做生产决策时，不能单纯地考虑本月制造费用，因为本月生产决策会对以后各个月的生产决策产生影响，而应考虑从本月初直到第4月低的生产制造成本费用（总指标），并且每月的生产决策只依赖于各月初存货量与以前造成的货存量无关，因此，这是一个5阶段多目标动态规划问题，适合采用逆序法建立多目标制造资源优化模型来解题，第1阶段是1月份，…，第5阶段是5月份。

3.2 建立多目标制造资源优化模型

定义符号如下：

表示在满足顾客合同需求量时，使冷热冲击试验机生产资源成本和库存费用达到最小;

基本方程为：

3.3 求解过程分析

3.3.1 决策变量

表示第个月的冷热冲击试验机生产量，表示第阶段开始的冷热冲击试验机存储量。

3.3.2 约束条件

对于每个月来说，生产量、需求量和月初库存满足如下关系：

下月初冷热冲击试验机库存量=本月初库存量+本月生產量-本月需求量

即类似状态转移方程：，分别如下。

第1个月：初始库存由给定值a确定;

由题意知，在此表示6月初的存储量，实际也是5月末的存储量，根据题意，5月末的库存量应该为零，这是一个隐含约束条件，是问题约束边界。生产能力限制：每月生产能力为100，由于产量限制为10的倍数，故可令，为整数且：。

3.3.3 目标函数

本题的目标是总费用最低。而总费用=每月的生产费用+库存费用，即：

3.3.4 数学建模

最终可得如下数学模型：

3.4 应用MATLAB求解

根据3.3节求解过程分析，编写如下代码：

Function u = DecisFun（k，x）

%% 函数功能说明

%产量的决策函数

%% 函数主体部分

q = 10*[6，8，10，9，8]; %每月的实际需求量

if q（k）-x < 0 %每月的实际需求量小于库存量时，产量为0～100

u = 0：100;

else

u = q（k）-x：100; %每月的实际需求量大于库存量时，产量为需求量扣除库存量～100

end

u = u（：）;

Function v =Sub0bjFun（k，x，u）

%% 函数功能说明

%求解阶段k的指标函数（成本）

%%函数主体部

c = [70，72，80，72，75];

v = c（k）*u+200*x;

Function w =TransFun（k，x，u）

%% 函数功能说明

%状态转移方程

%% 函数主体部分

q = 10*[6，8，10，9，8];

w = x+u-q（k）;

%% 函数功能说明

%利用动态规划逆序算法（DTGHNX）求解制造资源多目标优化配置问题

%状态转移方程

%%函数主体部分

q = 10*[6，8，10，9，8];

w = x+u-q（k）;

%% 文件主体部分

clc，clear %清除命令窗口，清除工作空间

x = nan*ones（14，5）; %x是10的倍数，最大范围0<=x<=130，共有5个阶段，故赋予x初值为14×5的矩阵

%按阶段（月）定义x的可能取值，由具体问题确定阶段数

x（1：7，1） = 10*（0：6）'; %1阶段（月）x的可能取值

x（1：11，2） = 10*（0：10）'; %2阶段（月）x的可能取值

x（1：13，3） = 10*（0：12）'; %3阶段（月）x的可能取值

x（1：14，4） = 10*（0：13）'; %4阶段（月）x的可能取值

x（1：9，5） = 10*（0：8）'; %5阶段（月）x的可能取值

[p，f]=DTGHNX（x， @DecisFun， @SubObjFun， @TransFun）; %由于Obj

Fun（v，f）=v+f，故輸入ObjFun省略

%输出结果

fprintf（'（1）各阶段（月）的库存、生产量和成本为：＼n'）

disp（' 序号库存产量成本'）

disp（p）

fprintf（'（2）总成本的最小值为（万元：＼n'）， disp（f）

disp（f）

3.5 结果分析

（1）执行结果，各阶段输出结果（截取部分数据），见下表2。

总成本见运行结果统计表3：下表中行1数值表示1月初库存量为0台时，5个月总成本为30070万元;行3数值表示1月初库存20台时，5个月总成本28590万元。

如输出结果所示，由各阶段（月）的库存，生产量和成本输出结果的第1个和第3个5行（红线框内）可以看出1月初无存货和有存货20台的最优生产决策，并由总成本输出结果的第1行和第3行可以得知，对应5个月的总成本分别为30070万元和28590万元。现将其归纳制成表4。

3.6 利用EXCEL验证MATLAB运行结果

为便于利用计算机辅助软件Excel验证求解，需要依据非线性动态规划问题的特点将关联数据导入Excel工作表。求解该模型的EXCEL电子表如表5和表6所示。

由表5可知，利用EXCEL求解的结果为1月初的库存为0时，各月的生产量分别为100台、100件、40台、100台和70台，总成本最低，值为30070万元。

如表6所示，当1月初冷热冲击试验机库存量为20台时，各月的生产量分别为100台、100台、20台、100台与70台，总成本最低，值为28590万元。

综上与MATLAB运行结果对比，结果完全一致，验证了优化配置模型可行性和自编算法的正确性，完成了顾客生产定制计划，达到了预期目标。

4 结论

本文通过多目标资源优化问题的进行研究可得到如下成果：

（1）分析了多目标资源优化配置模型形成过程，按照经济效益最先性原则，提出一种非线性动态规划算法，构建了以资源消耗最少，经济效益获取最大目标资源优化配置模型，为解决多目标资源优化问题提供了一种新思路。（2）以根据顾客要求而定制的生产计划订单为例，通过实证分析，验证了生产定制多目标资源优化配置模型可行性和有效性。（3）针对多目标资源优化配置模型求解问题，运用自编的MATLAB算法求解，然后用EXCEL验证，验证了该算法的正确性，为类似多目标资源优化配置问题的求解提供了一种新方法。

本文分析了多目标制造资源优化模型形成过程，借鉴了已有的资源优化配置模型，针对制造资源受限对生产计划定制的影响，利用非线性动态规划算法，建立一套制造资源优化模型，最后通过案例分析验证了该方法的有效性，为今后展开多目标多层次制造资源优化奠定了基础。

参考文献：

[1]房亚东，杜来红，何卫平等.网络化制造环境下多维度制造资源建模技术研究[J].计算机应用研究，2009，26（02）：553-556.

[2]冀阿强，段晓峰.面向云制造的制造资源模型研究[J].中国制造业信息化，2012，41（17）：5-8.

[3]张中伟，唐任仲，陶俐言.基于滚动计划的动态企业资源优化模型[J].计算机集成制造系统，2016，22（02）：516-528.

[4]蓝伯雄，姜楠.基于滚动计划的动态企业资源优化模型[J].运筹与管理，2010，19（03）：127-143.

[5]葛家家，李贤功，胡婷.服务型制造的项目资源优化模型研究[J].科技管理研究，2015（19）：211-215.

[6]包北方，杨育等.产品定制制造资源优化配置[J].计算机集成制造系统，2014，20（08）：1807-1818.

[7]蒋南云，张琳，张英豪等.基于Jackson排队网络的出厂检验环节资源配置优化[J].工业工程与管理，2016，12（01）：45-53.

[8]付银环，郭萍等.基于两阶段随机规划方法的灌区水资源优化配置[J].农业工程学报，2014，45（05）73-81.

[9]李奥典，唐德善等.基于图论的丽水市多水源供水配置模型研究[J].华东交通大学学报，2016，33（01）：107-113.

[10]胡运权，郭耀煌.运筹学教程[M].北京：清华大学出版社，1998.