轨道交通大跨度曲线连续梁曲线效应及应力扰动区设计研究

2019-10-21陈怀智

现代城市轨道交通 2019年9期

陈怀智

摘要：南京宁溧城际轨道交通高架 60m + 100m + 60m 連续梁桥跨度大、桥面窄、曲线半径小，其曲线效应导致结构产生多种变形耦合等问题。为此，对其进行不同梁格模型对比分析，并引入应力扰动区概念对构造复杂部位进行细部分析，研究其受力规律及构造要点。

关键词：轨道交通;桥梁;曲线连续梁;梁格模型;曲线效应;应力扰动区

中图分类号：U445

0 引言

轨道交通桥梁具有受力复杂、列车荷载大、设计施工难度高等特点，而处于小半径曲线线路上的大跨度梁式桥，由于曲线效应将导致结构产生多种变形耦合问题，包括梁部的轴向变形与平面内弯曲耦合，竖向挠曲与扭转耦合等，以及存在“外梁超载，内梁卸载”问题[1]。另一方面，由于轨道交通桥面宽度相对公路桥较窄，一般在10 m左右，支座数量较少，一般设置双支座，再加上悬臂施工带来的结构体系转换。这些因素的叠加，使得梁体水平径向位移过大、梁体翘曲、墩梁固结处开裂、支座反力不均匀等工程问题更加突出[2-3]。

南京宁溧城际跨越常马高速处，采用60m + 100m

+ 60m连续箱梁斜交跨越，桥型布置图见图1，桥梁位于曲线段，桥上线路曲线半径分别为650m和653.7m，线间距3.7 m，采用挂篮悬臂施工法进行施工。由于其径跨比较小，变形耦合较为突出，曲率扭转效应使得曲线内外侧支反力、挠度及梁截面应力都有所不同，为此分别采用3种计算分析模型对结构进行分析，包括直线单梁模型、曲线单梁模型以及曲线梁格模型，以此来精确判定曲线梁的曲线效应影响。

另外，轨道交通大跨度梁结构空间局促、构造复杂，预应力齿块锚固区、梁端锚固区、横隔板等处受力复杂，在铁路桥梁规范以及以往的公路桥梁规范中，均没有具体的计算规定，设计中缺乏明确的计算依据。为准确计算上述区域的结构受力，引入应力扰动区的概念，对各种力学性状进行详细检算，以此指导并加强具体构造设计。

1 设计概况

（1）设计标准。设计行车速度100km/h，地震动峰值加速度0.10 g，分块式无砟轨道结构高度0.54 m，列车荷载：B型列车、6节编组，车辆定距10.3 m，固定轴距2.2 m，车辆最大轴重P = 140kN，最小轴重P = 80kN，见图2。

（2）桥梁构造。桥跨布置为60m +

100 m + 60 m预应力混凝土连续梁，梁缝每侧0.15 m，桥梁全长219.7m，桥面宽9.0m。设计采用单箱单室直腹板截面，截面形式见图3。

（2）结构配束。本桥采用三向预应力体系，纵横向预应力钢束采用高强度低松弛钢绞线，其标准强度fpk = 1860MPa，弹性模量E0 = 1.95×105MPa，采用高密度聚乙烯塑料波纹管成孔。

2 曲线效应分析模型

曲线梁与直线梁最明显的区别在于扭转[4-5]，对于变截面连续梁桥，跨长、抗弯刚度是影响受力的主要因素，而曲线梁的圆心角、径跨比、桥宽与曲率半径比、弯扭刚度比、扇性惯矩都将影响其受力[6-7]。为比较曲线梁的曲线效应影响，分析曲梁扭转效应导致的曲线内外侧支反力、挠度及梁截面应力的不同，采用Midas Civil 2015分别建立直线单梁模型、曲线单梁模型、曲线梁格模型等3种计算分析模型。3种模型采用了相同的设计参数（结构组、边界条件及荷载工况等）及施工阶段规定。恒载包括自重、预应力、混凝土收缩和徐变、二期恒载，由于基础持力层位于岩层，恒载不计支座沉降对支反力的影响。

2.1 直线单梁模型

本模型按直线梁建模，不考虑曲线因素，支座根据实际布置位置按双支座进行模拟，与主梁节点采用刚性连接。模型见图4。

2.2 曲线单梁模型

本模型考虑曲线因素进行单梁建模分析，这里曲线实际上指的是以直线带曲线，模型见图5，2个节点之间仍为直线，但建模分析的每个节点都在半径为650m的曲线上。

2.3 曲线梁格模型

梁格法的特点是用一个等效的梁格来代表桥梁的上部结构，即假定把上部结构的抗弯、抗扭刚度集中到最邻近的梁格内[8]：纵向刚度集中到纵向构件内，横向刚度集中到横向构件内。本模型采用2根纵梁和若干横梁组成的梁格来模拟单箱单室截面的曲线梁格模型，图6为曲线梁格模型（左纵梁），实际结构的纵向刚度集中于2根纵向梁格构件内，而横向刚度则集中于横向梁格构件内。

3曲线效应计算分析

3.1 最大悬臂状态

3.1.1 恒载弯矩与位移

最大悬臂状态是施工中的控制状态之一，为此，应用3个模型进行悬臂施工阶段仿真计算，对比最大悬臂状态下仅考虑计算恒载效应与同时计算“预应力+自重”效应的不同，并讨论预应力作用对曲线效应的有利因素。

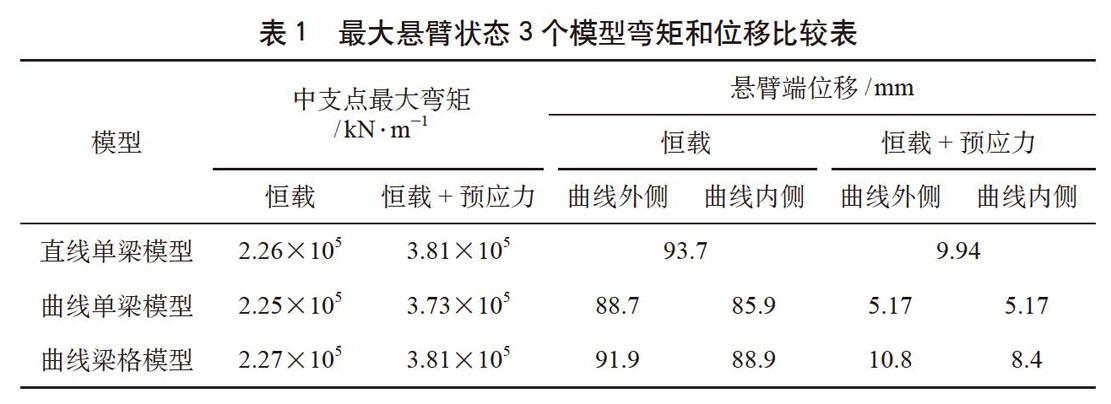
3个模型对比计算情况见表1，由表1可知，上述2种作用组合下，中支点弯矩相差均小于5%。自重下的悬臂端位移达到约90 mm，考虑实际施加预应力之后，悬臂端位移减小到约10 mm。此外，顶底板曲线内、外侧挠度不一致，但差别不大。说明3种模型对整体效应下的结果基本一致。

3.1.2 恒载截面应力

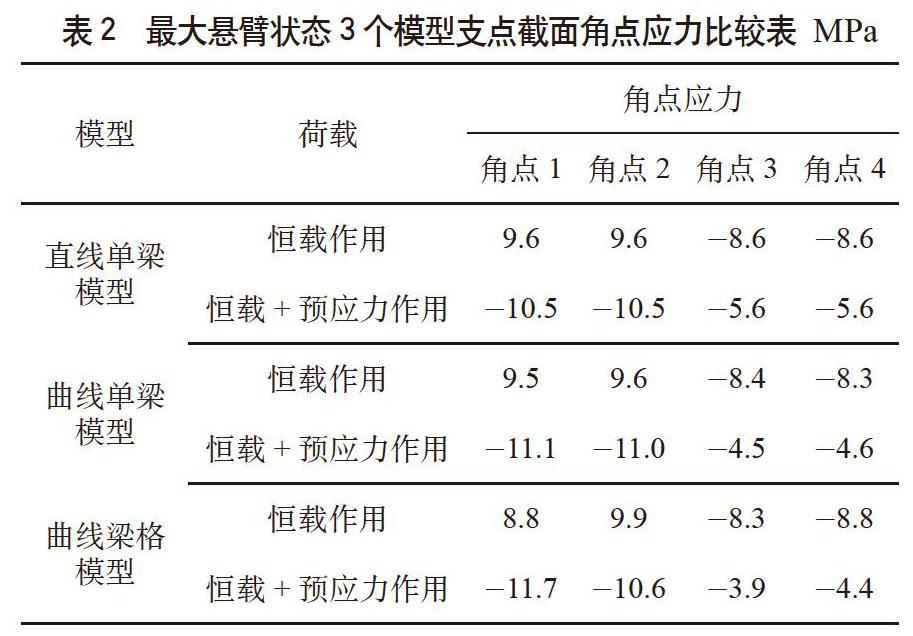
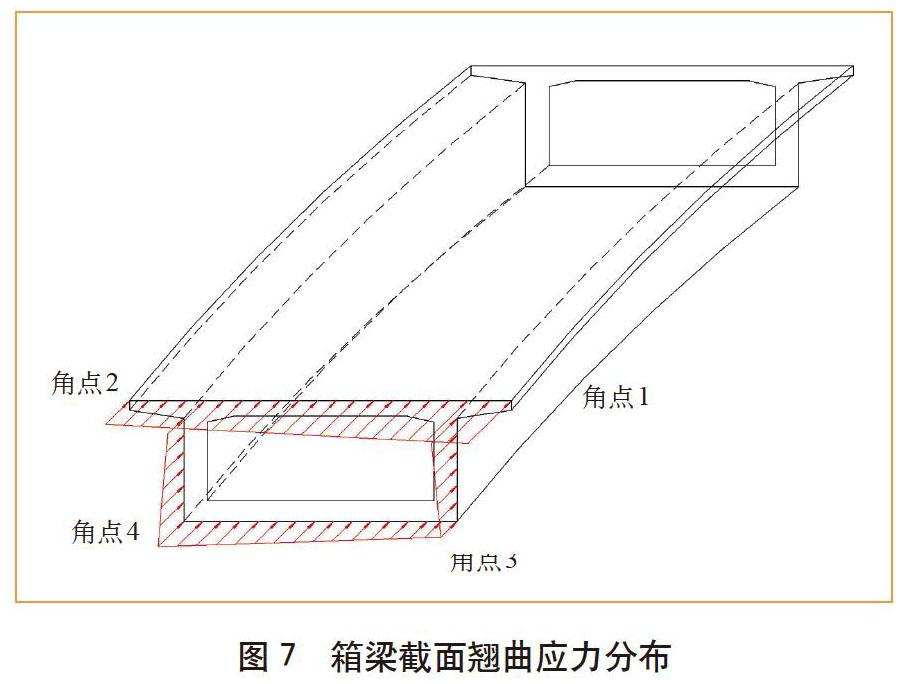
曲线梁由于扭转效应将引起截面翘曲应力，使得截面内外侧应力产生差异，如图7所示，图 7中4个截面角点分别为顶板内侧角点1、顶板外侧角点2、底板外侧角点3、底板内侧角点4。表2给出了支点截面4个角点应力计算情况。

3个模型对比计算情况见表2，由表2可见，曲线单梁及梁格模型能够反映出扭转引起的截面内外侧应力差，顶板曲线内侧压应力大于外侧，而底板曲线内侧压应力小于外侧;顶底板曲线内、外侧应力不一致，相差约10%左右。

3.1.3 支座反力

在最大悬臂状态直线梁模型没有扭矩，左右侧支座竖向支反力均为14 409 kN;曲线梁模型曲线外侧支反力为11 444 kN，曲线内侧竖向支反力为17 377 kN，且存在横向支座反力，为2 868 kN，曲线内侧支反力比曲线外侧支反力大 6000kN左右。这使得悬臂端浇筑临时固结支架时的曲线内外侧支反力不同，支架设计时应注意。

3.2 成桥状态

3.2.1 恒载弯矩分布

连续梁成桥后，预应力在抵消恒载产生的弯曲和剪切效应之后，梁体应处于恰当的内力状态，使之平衡一定比例的活载、温度等作用效应，以抑制桥梁长期下挠。在合理受弯状态下，梁体根部区域储备一定量的正弯矩，用以抵抗活载、温度等在根部截面产生的负弯矩;跨中部位储备一定量的负弯矩，用以抵抗在长期运营中活载、温度等可变荷载效应造成的不利影响[9]。

与直线梁模型相比，曲线单梁模型在“恒载+预应力”工况下，由于扭转效应，中跨跨中为正弯矩，未能储备一定量的负弯矩;而曲线梁格模型中跨跨中外曲线弯矩为正，内曲线弯矩为负。见图8。

3.2.2 成桥状态应力

成桥状态在恒载工况下拉压应力均未超限，且在边跨以及中墩墩顶由于扭转产生的角点应力不一致所导致的差别很小;而在中跨跨中受扭转影响稍大，顶板以及底板曲线内外侧的应力差约 1 MPa。见表3。

3.2.3 支座反力

直线单梁模型支反力总和与曲线梁格模型是一致的，但每个支反力结果与曲线单梁模型相差10%左右，曲线要素对支反力的影响很显著。曲线单梁模型和曲线梁格模型计算结果相差小于5%。见表4。

从曲线单梁及梁格计算结果看，中墩内侧支座的支反力大于外侧支座的支反力，相差约20%，边墩内侧支座的支反力小于外侧支座的支反力，相差约7%;对于大跨度曲线连续梁，曲线要素对支反力的影响很显著;中墩内外侧反力特点与简支梁不同，反力值差别的大小跟曲线半径、连续梁跨度、支座间距均相关[10-11]。通过对不同支座间距的支反力比较，加大双支座间距能在一定程度上降低曲线连续梁桥内外支座反力的差值，但过大的支座间距对支点处构造有影响，应综合考虑，可通过设置支座预偏心减少反力差。见表5。

值得注意的是，由于大跨度曲线梁的截面变化较大，中墩位置处主梁的抗扭刚度很大，中墩处内侧支反力比外侧支反力相差较大，而端支座处的内、外侧支反力则相差不大。这与截面不变的曲线梁桥情况有所不同，相关文献也有类似研究结论[12]。

3.2.4 温度力

在整体升降温工况下，曲线梁桥会产生径向和切向反力，其中切向反力较大，为192 kN，见表6。这是由于整体升温下曲线外侧变形较大，受到曲线内侧梁体的阻挠，引起支座产生反力来抵抗这个阻力。此时应校核支座的抗剪能力是否控制设计，并将其作为温度附加力与制动力组合进行内力、应力验算。

3.3 3 种模型比较

（1）从3种模型的主要结果看，在R = 650m的曲线半径条件下，大跨度连续梁的曲线效应明显。曲线梁格模型能够较好地反映曲线梁的受力特征，如曲线梁桥的“弯扭耦合”作用使得曲线梁桥内外边缘挠度不一致以及截面角点应力不同。

（2）由于轨道交通梁宽度较窄，曲线单梁模型和曲线梁格模型总体受力计算结果相差较小，采用曲线梁格模型，在各阶段的应力体现出内外侧差异，在结构配束设计时应加以区别。

（3）曲线梁桥的中墩支反力曲线外侧小于中墩内侧，而边墩支反力曲线外侧大于曲线内侧，在最大悬臂状态时曲线内侧支反力比曲线外侧大 6 000 kN，这使得悬臂施工临时支墩内、外侧立柱受力不一致。

（4）曲线梁格模型在成桥状态时，由于扭转效应，中跨跨中可能处于正彎矩状态，不利于抵消后期收缩徐变发展的影响。

4 应力扰动区分析

4.1 应力扰动区分布

自上世纪80年代以来，国际工程界倡导将混凝土结构划分为 B区和 D区。B区指截面应变符合平截面假定的区域，按“梁式体系”计算;D区，即应力扰动区，指截面应变分布不符合平截面假定的区域[13]，一般位于集中力作用点附近或几何尺寸发生突变的部位。这些部位的受力十分复杂，具有几何构造上的不连续或力流扰动的特点。其中桥梁典型的应力扰动区包括齿块锚固区、变截面梁桥跨中底板径向力作用区、端部锚固区等，见图9。

桥梁工程的实践表明，由于应力扰动区在受力上的复杂性，加上缺乏理论设计指导，是各类病害的高发区。一旦作为结构关键受力部位出现病害，将影响整个桥梁结构的使用性能甚至安全性。由于铁路规范并未明确相关计算内容，本桥在设计时参考了《公路钢筋混凝土及预应力混凝土桥涵设计规范》[14]（送审稿）中关于应力扰动区的设计计算及构造规定，对齿块锚固区进行了详细的分析。

4.2 齿块锚固区分析

由于齿块锚固区存在着几何形体上的突变、集中锚固力的作用以及预应力钢束局部弯曲引起的径向力作用，预应力集中锚固力一般在数十吨至数百吨量级，锚固力扩散带来的受拉效应常常引起锚固区的开裂[15]。锚固区内存在如下5种典型受拉效应[16]，见图10。

（1）齿块锚下横向拉应力分布，起因于“锚下劈裂效应”，包括齿块高度和厚度方向的劈裂效应：锚下劈裂区的拉力T b，d。

（2）齿块与底板交接处的拉应力集中，起因于“剥裂效应”：齿块悬臂根部区的拉力T s，d。

（3）锚后拉应力集中现象，缘于“锚后牵拉效应”：锚后牵拉区的拉力T tb，d。

（4）底板下缘拉应力区，缘于“局部弯曲效应”：边缘局部弯曲区的拉力T et，d;

（5）预应力钢束转向区域拉应力集中的现象，来源于“径向力效应”：径向力作用区的拉力T R，d。

后张预应力构件三角齿块锚固区内5种受拉效应的拉力设计值，可按下列公式计算：

锚下劈裂效应拉力T b，d：

（1）

式（1）中，d为锚固力中心至齿板上边缘的垂直距离;a为预应力钢筋的倾角;Pd为预应力锚固力设计值。

根部悬臂效应拉力T s，d：

T s，d = 0.02 Pd （2）

锚后牵拉效应拉力T tb，d：

T t b，d = 0.2 Pd （3）

边缘弯曲效应拉力T et，d：

（4）

径向作用效应拉力T R，d：

T R，d =Pda （5）

依据上述公式，对实际设计的配筋情况（图11）进行检算，结果如表7。由表7可以看出，按照习惯配置的钢筋存在一定富裕，可以进行优化，同时，局部弯曲处配筋往往需要加强，这也是实际工程中经常发生混凝土崩裂的位置[17-18]。

4.3 应力扰动区钢筋布置

4.3.1 齿块锚固区

根据齿块锚固区内5种受拉效应的拉力设计值，除配筋计算，齿块构造及钢筋布置还应符合以下原则[19-20]。

（1）齿块布置应统筹考虑，对于2个比较靠近的独立齿块，宜合并在一起;靠近腹板的独立齿块，宜和腹板连接，形成角隅三角齿块，并加设侧向闭合箍筋。

（2）齿块锚下局部承压区内应配置间接钢筋。

（3）齿块锚下应配置伸入箱梁板壁内的闭合式箍筋，以抵抗锚下劈裂力。

（4）齿块锚后应在壁板上侧和下侧配置牵拉钢筋，以抵抗锚后牵拉力;应对称布置在力筋轴线两侧各1倍齿块宽度范围之内，并应具有足够的锚固长度。

（5）齿块预应力筋弯曲区域应配置竖向箍筋，以抵抗径向力。

齿块锚固区钢筋布置见图12，图中h为齿块高度。

4.3.2 腹板下弯束锚固区

后张锚固区是典型的应力扰动区，在预应力锚固集中力作用下，存在局部承压和应力扩散问题，其锚固的抗裂性和安全性也是结构设计关键内容之一。参考公路规范，锚固区普通钢筋构造应满足下列要求。

（1）锚下局部承压区内应配置间接钢筋。对于平板式锚垫板，应配置不少于4层的方格网钢筋或不少于4 圈的螺旋筋;对于带喇叭管的锚垫板，应配置螺旋筋。

（2）锚下总体区应配置闭合式箍筋以抵抗竖向劈裂力，钢筋间距不应大于100mm。

（3）沿梁端截面边缘应配置抗裂钢筋以抵抗边缘剥裂力;在大偏心锚固情况下，锚固端面钢筋宜弯起并延伸至纵向受拉边缘以抵抗边缘纵向拉力。

5 结论及建议

（1）由于轨道交通桥梁宽度较窄，对于支座反力、位移、应力应采用不同类型模型，其计算精度各有不同。采用曲线梁格模型进行设计计算，可以较好地反映曲线梁的受力特征，如，曲线梁桥“弯扭耦合”作用，使得曲线梁桥内、外边缘挠度不一致以及截面角点应力不同。对于大跨度曲线连续梁，设计时需考虑曲线效应，宜采用曲线梁格模型。

（2）对于曲线连续梁，应重视应力扰动区的设计，包括齿块锚固区、变截面梁桥跨中底板径向力作用区、端部锚固区等。

参考文献

[1] 徐升桥. 预应力混凝土连续曲线箱梁桥的分析与设计[J]. 铁道标准设计，1994，13（3）.

[2] 张继尧，王昌将. 悬臂浇注预应力混凝土连续梁[M].北京：人民交通出版社，2004.

[3] 徐涛. 大跨曲线铁路梁桥空间受力研究[D]. 湖南长沙：中南大学，2012.

[4] 邵容光. 曲線梁桥按直线梁桥近似计算的判别条件[J]. 东北公路，1991，1（20）.

[5] 刘小燕，吴飞，肖培香. 曲线梁桥桥空间应力特性分析[J]. 中外公路，2010，14（30）.

[6] 李乔. 薄壁曲线箱梁的空间分析理论[D].四川成都：西南交通大学，1988.

[7] 吴西伦. 弯梁桥设计[M]. 北京：人民交通出版社，1990.

[8] 邵容光，夏淦. 混凝土弯梁桥[M]. 北京：人民交通出版社，1994.

[9]姚玲森. 曲线梁桥的实用计算方法[J]. 土木工程学报，1982，15（3）.

[10] 方诗圣，肖兵，张吉烁. 支座布置形式对曲线梁力学性能的影响[J]. 世界桥梁，2011，20（4）.