种群规模对蝙蝠算法性能的影响

2019-10-21郭小雪贺兴时

纺织高校基础科学学报 2019年3期

郭小雪,贺兴时,罗东

(西安工程大学理学院,陕西西安 710048)

0 引言

蝙蝠算法(BA)[1]是杨新社教授于2010年基于群体智能[2]提出的一种启发式搜索算法。目前,BA作为一种新型的群智能优化算法,已成功应用于很多领域[3-6],但与其他群智能优化算法一样,也存在收敛速度慢、求解精度低的问题。因此，通过优化算法性能,避免算法出现早熟现象,提高算法自身寻优能力具有重要意义。

目前,蝙蝠算法的研究主要集中在算法的改进以及参数的设置。在算法改进方面,学者们分别从对蝙蝠个体进行不同变异，调整蝙蝠个体速度更新策略以及在蝙蝠学习机制中引入权重策略等不同角度对BA的性能进行了优化改进,提高了BA的求解精度和收敛速度。这些研究[7-9]中种群规模的设置分别为50,40和30,对种群规模大小的选择缺乏理论指导。

在参数设置方面,文献[10-13]分别从影响蝙蝠音量和脉冲发生率变化的参数,速度和位置的相关算子以及惯性权重的值三方面分析了不同参数对BA性能的影响,并得到最优参数,提高了BA的性能。但是，这些研究均忽略了种群规模对BA收敛速度和求解精度的影响。本文将分别从算法收敛速度、求解精度、全局搜索能力[14]、收敛时间4个方面分析不同种群规模对BA的影响,并对所得结论进行验证。

1 BA性能的评估指标和种群规模

1.1 BA性能评估指标

(1) 收敛速度在数值分析中,收敛序列向其极限逼近的速度称为收敛速度。用于最优化算法中,被定义为一个迭代序列向其局部最优值逼近(假设计算过程收敛,并能达到最优值)的速度,是评价迭代法性能的一个重要指标。

(2) 求解精度收敛序列逼近其最优值的程度,即表示算法寻得的最优值与实际最优值的接近程度。

(3) 全局搜索能力算法独立运行M次,得到满足算法收敛精度的解的总次数为N,则A=N/M表示全局搜索能力。

(4) 收敛时间收敛序列逼近其最优值或达到收敛精度的运行时间。

1.2 种群规模

在原始蝙蝠算法中,种群规模[15]始终是固定不变的。不过，不同问题对种群规模选取有不同的需求,使得种群规模在一些问题的寻优过程中表现的不合理。特别是蝙蝠算法在解决一些具有较大群体规模的实际问题时,需要对很多个体进行适应度值的计算和评估,导致算法的迭代过程运行缓慢,很难达到预想中的寻优效果。

种群规模是蝙蝠算法的一个重要参数,对算法的寻优能力和求解精度有较大影响。如果选取的种群规模较大,算法会以更大的可能性搜索到全局最优解;如果选取的种群规模较小,会导致搜索范围减小,算法在短时间内很难收敛到全局最优解。

为了分析不同种群规模对蝙蝠算法性能的影响,本文采用具有代表性的单峰函数(Zakharov函数)和多峰函数(Ackley函数)分析种群规模对算法收敛速度、求解精度、全局搜索能力的影响以及种群规模对单峰函数(Zakharov函数和Sphere函数)收敛时间的影响。

2 仿真实验

算法参数设置如下:α=β=0.9,响度A在[1,2]之间初始化,脉冲发射率R在[0,1]初始化。 Ackley函数、Zakharov函数和Sphere函数的最大迭代次数分别设置为1 000次、100次和1 000次。测试函数及迭代结果见表1。

表 1 测试函数

2.1 种群规模对算法收敛速度和求解精度的影响

在分析种群规模对算法收敛速度和求解精度的影响时,固定最大迭代次数不变,依次增大种群规模,观察收敛速度和求解精度随着种群规模不断增大的变化。为了分析不同维度下种群规模对算法搜索精度的影响,将问题维度设置为30，60，100和200等4种情况。对于求解单峰函数(Zakharov函数)问题,算法的种群规模设置为20，50，100，200和500等5种规格,共20种组合,每一种组合算法独立运行50次并取其均值；对于求解多峰函数(Ackley函数)问题,算法的种群规模设置为50，100，200，300，400和500等6种规格,共24种组合,每一种组合算法独立运行50次并取其均值。图1为Ackley和Zakharov函数种群规模和收敛速度的关系,表2和表3分别为Zakharov和Ackley函数种群规模与算法求解精度的关系。

表 2 Zakharov函数种群规模与算法求解精度的关系

注：最优解为0。

表 3 Ackley函数种群规模与算法求解精度的关系

注：最优解为0。

(a) Ackley

(b) Zakharovarov图 1 种群规模和收敛速度的关系

从图1可以看出,对于求解Zakharov函数和Ackley函数问题,算法的收敛速度都是随着种群规模的增大而加快。但是，不同的函数具有不同的下降速率曲线,下降速率曲线呈波动型下降,而非严格递减。对于Zakharov函数问题,当种群规模大于50时,算法的收敛速度对种群规模不敏感；对于Ackley函数问题,当种群规模大于100时,算法的收敛速度对种群规模不敏感。

由表2和表3可以看出,当维度固定时,无论求解单峰函数问题还是多峰函数问题,随着种群规模的不断增大,蝙蝠算法的搜索精度不断提高;当种群规模固定时,随着维度的增加,算法的求解精度无明显变化规律,说明维度对算法的搜索精度影响不大。同时可以看出,对于Zakharov函数问题,在维度一定时,当种群规模大于100,算法的搜索精度的变化不大;对于Ackley函数问题,当种群规模大于300时,算法的搜索精度趋于稳定。

2.2 种群规模对算法全局搜索能力的影响

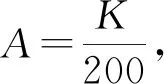
从图2可以看出,当种群规模增大时,不论是求解Zakharov函数问题还是Ackley函数问题,蝙蝠算法的全局搜索能力均有所提高。但是，当种群规模达到一定值后,全局搜索能力趋于稳定值1,即算法独立运行的总次数和满足算法收敛精度的解的次数相等。

(a) Ackley

(b) Zakharov图 2 种群规模与全局收敛能力的关系

2.3 种群规模对算法收敛时间的影响

在分析不同种群规模与算法收敛时间的关系时,设置收敛精度一定,运行程序,记录算法满足该收敛精度所需的运行时间。由于多峰函数大多有局部极值,容易陷入局部最优,难以计算其收敛时间,因此仅分析具有代表性的单峰函数的收敛时间。选取Zakharov和Sphere 2种单峰函数，分析种群规模与算法收敛时间的关系，结果见表4。

由表4可以看出,对于Zakharov函数问题,当维度固定时,随着种群规模的扩大,算法的收敛时间逐渐减小;当种群规模达到100时,算法的收敛时间随着种群规模的扩大开始递增。当种群规模固定时,算法的收敛时间随着维度的增加不断变大。对于Sphere函数问题,当维度固定时,算法的收敛时间随着种群规模的增大而增加;当种群规模固定时,随着问题维度的增加算法收敛时间也变大。

在寻找问题的最优解时,若侧重加快收敛速度,则求解Zakharov函数问题时算法的种群规模可设为50左右,求解Ackley函数问题时算法的种群规模可设为100左右；若侧重提高搜索精度,则求解Zakharov函数和Ackley函数问题时算法的种群规模可分别设为100和300;若侧重增强全局搜索能力,则求解Zakharov函数问题时算法的种群规模可设为50左右,求解Ackley函数问题时算法的种群规模可设为100左右。若侧重减小运行时间,则求解Sphere和Zakharov函数问题时算法的种群规模可设为50～100。

表4Zakharov及Sphere函数种群规模与算法收敛时间的关系

Table 4 The relationship between population size and algorithm convergence time of Zakharov and Sphere functions

在评估算法性能时,应综合考虑影响算法性能的4个因素,不应只考虑其中一种因素,即应取以上4个种群规模的均值,才能更准确的评估算法的性能。对于求解单峰和多峰函数问题,算法的种群规模应分别设为70和170左右。

2.4 T检验

T检验主要用于样本含量较小,总体标准差σ未知的正态分布,是用t分布理论来推论差异发生的概率,从而比较两样本均值的差异是否显著。 T检验分为3种方法:单一样本T检验、配对样本T检验和独立样本T检验。本文使用独立样本T检验,用于观察两组数据的平均值有无差异。

为了验证所得结论的准确性,对表1中的4个单峰函数和4个多峰函数在种群规模分别为40，70及40，170等2种情况下进行仿真测试，并假设原始蝙蝠算法种群规模为40。分别独立运行100次,这样在每个测试函数问题上,2种种群规模下算法均有100个样本；取其均值,利用T检验法比较分析2种种群规模下算法的性能。结果表明,这8个函数在种群规模分别为70和170时算法的性能最好。