大跨度穹顶结构在风载荷作用下风振系数随厚度变化的研究
2019-10-21瞿宇
瞿 宇
(中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014)
有限单元法在土木工程领域中得到了广泛的应用,风灾是对建筑物造成最严重损失的灾害之一,纵观各个案例得出,在建 (构) 筑结构设计中,结构的抗风设计是不可忽视的重要部分,风荷载是各种设计建 (构) 筑物的重要设计荷载。大跨度空间结构特点为阻尼小、重量较轻、自振频率较低、柔性较大,尤其对风荷载较为敏感。
现在结构的厚度越来越小和质量越来越轻,使对风的反应越敏感,因此风作为大跨度空间的控制荷载在结构设计时尤为总要。
风荷载的常见特点:观测记录表明即时风速包括两种成分:周期在10 min以上的均匀风和周期只有几秒钟的脉动风。通常将风荷载在工程实际应用中作为静力风与动力风的共同作用来考虑。
1 风荷载的常见特点
观测记录表明即时风速包括两种成分:周期在 以上的均匀风和周期只有几秒钟的脉动风。通常将风荷载在工程实际应用中作为静力风与动力风的共同作用来考虑,如图1所示。
图1 静力风与动力风共同作用下建筑物
2 模拟风速时程
均匀风是在特定的时间内,方向和风力大小等不随时间改变的量,作用在结构上由均匀风导致的风荷载,称为静力风荷载。而脉动风则随时间按随机规律变化,要用随机振动理论来处理,风的模拟主要是针对脉动风而言。
由于大跨屋盖纵向和横向尺度大,竖向尺度小的特点,因此,竖向刚度小而水平刚度大。大跨屋盖应核算屋盖结构在竖向风作用下的静力和动力响应,不能忽略竖向风荷载给结构带来的影响和作用。本文模拟的脉动风将采用垂直风速谱和水平风速谱一起的作用和影响。本文采用Panofsky谱垂直风速谱,采用Davenport谱作为水平脉动风速谱。
而对于风速时程的模拟方法主要有谐波叠加法和线性滤波法。文中应用简谐波累加法模拟风谱。依据Shinozuka理论成果,随机过程v(t)的范本根据下列公式来模拟:

工程中,一般实测的记录为风速,但实际应用时要将风速转换为风压,这就涉及了如何把风速转换为风压这个问题。根据Wiener-Khint chine定理和脉动风压功率谱的定论,可以得出脉动风速功率谱和脉动风压功率谱的互换联系。并依此公式可以将脉动风压模拟出来。转换关系为:

根据上述理论,应用Matlab软件编制代码模拟沈阳区域60 m海拔处的风情况,风速基本情况取v10=25 m/s,风压基本情况按天津区域为ω0=0.50 kN/m2。地面粗糙度为C类别,地面粗糙的系数k=0.015,依据相关规范,α=0.2为地面粗糙度指数。
大气间的密度ρ=1.29 kN/m3,频率取样点数N=1 024,风速模拟时间为200 s,时间步长为0.2 s,频率ω的截取区间的确定一般是根据风速谱的特点。查阅大量的文献后,发现通常位于高频区的风速谱衰减得非常快,一般超过1 Hz后值较小,对结果影响不明显,超过5 Hz以后,所包含的能量已经很少。故由Davenport谱和Panofsky谱特点得出脉动风速的能量主要集中在很窄的(0~5)区段内,故取ω∈(0~5)。
3 风谱验证
鉴于脉动的风速时程是一个随机过程,这些用于对风速时程正确性的结果检测一般都是基于统计意义上的,也就是在生成的风速时程时要在统计特性上与目标谱相符。同样,也可以进行相关函数的检测,本质上两者是没有区别的。
检验谱密度,第一应根据生成的风速时程进行傅立叶快速变换,相关函数因此可以得到。再进行傅立叶变换求得相关函数按维纳-辛钦关系公式。水平脉动风速谱的模拟图如图2所示。可以看出,风速时程的模拟谱与目标谱吻合,模拟效果较好。

图2 水平功率谱对比
4 算例解析
算例中,选取辽宁天作建筑工程有限公司的工程例子:跨度d为40 m、半径r为20 m的薄壳穹顶 (其中加劲肋为48个)进行计算模拟分析,加劲肋规格2δ×40δ=77.8 mm×156 mm,薄壳穹顶结构整个支撑在高为60 m的支座上且支座为刚性。在有限元分析过程中,薄壳单元作为壳体部分分析单元来采用,当量密度ρ=352 kN/m3,弹性模量E=215 GPa,泊松比μ=0.25。加劲肋部分采用梁单元,弹性模量E=215 GPa,泊松比μ=0.25,当量密度ρ=7 800 kN/m3。模型的计算简图和基本情况如图3所示,在分析中对各种不同尺寸厚度的结构进行了分析计算。

图3 穹顶模型计算简图及底边约束图
将脉动和均匀风荷载施加到5种厚度不同的穹顶结构上,通过选取计算薄壳体中心顶点的一组径向节点进行风振系数,风振系数公式为:
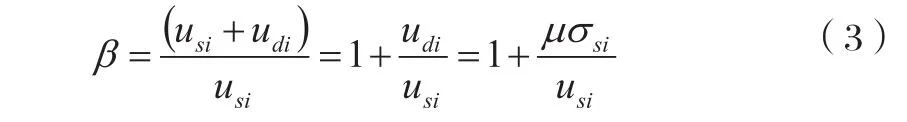
根据上述理论,结构阻尼采用Rayleigh阻尼,利用有限元计算瞬态分析,得到所选取的径向节点的位移响应均方根值和位移值,将其分别代入相关公式,得到风振系数平均值和系数值,如图4所示。
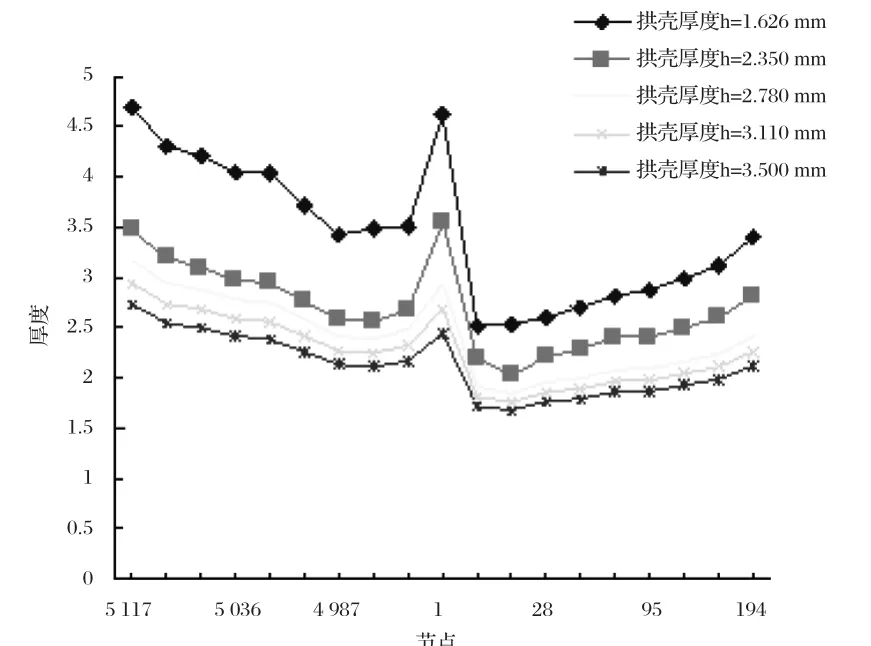
图4 不同拱壳厚度风振系数值
图4 中观察出,拱壳厚度对穹顶结构的影响非常大。一个模型下,矢高、跨度、矢跨比相同,将拱壳的厚度增加,位移风振系数将逐渐减小,这就说明增加厚度是有利于结构来抵抗风荷载。而跨中部位的风振系数出现了突变,也说明了薄弱部位位于跨中部位,因此,在结构设计时应重点考虑此跨中位置。
5 结语
(1) 与线性滤波法相比,谐波叠加法是人工模拟脉动风速时程的有效方法。
(2) 在20 m矢高和40 m跨度的情况中,受风荷载影响最大为跨中部位,应在结构设计时重点注意该部位。
(3) 当矢高、跨度不变时,风振系数随厚度减小而变大,也就是说厚度越大越有利。然而厚度的变大会增加整体的自重,对结构的抗震设计和强度又带来了挑战。因此,在进行穹顶结构的设计时,要综合考虑各种因素的影响。
