平面直角坐标与极坐标转化的圆锥曲线问题探讨

吴美林

（贵州省毕节市二中，贵州 毕节 551700）

一、两种坐标的定义

平面直角坐标：两条互相垂直，并且有公共原点的数轴。其中横轴为X轴，纵轴为Y轴。此坐标系平面直角坐标系。

极坐标系：在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。由平面内由极点、极轴和极径组成的坐标系，称为极坐标系。

二、极坐标系到直角坐标系的转化

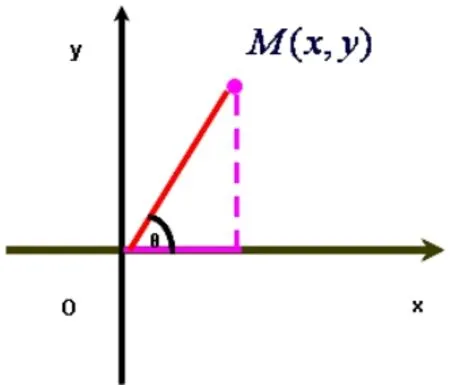
说明：1上述公式即为极坐标与直角坐标的互化公式

3互化公式的三个前提条件： 极点与直角坐标系的原点重合；，极轴与直角坐标系的x轴的正半轴重合；ƒ 两种坐标系的单位长度相同。

三、圆锥曲线由平面直角坐标转化为极坐标的几个问题

（一）椭圆

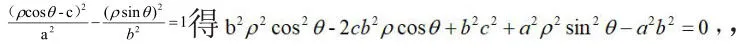
（二）抛物线

（三）双曲线

四、直接推导圆锥曲线的极坐标方程

L由圆锥曲线的统一定义：是动点到焦点的距离和动点到准线的距离之比为一定值常数e，该动点轨迹为圆锥曲线。如图

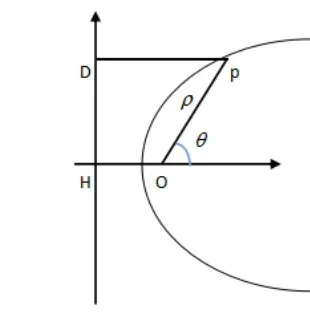
今以一定点O为极点，使极轴垂直于定直线建立极坐标，取圆锥曲线上一点P。由图极轴与定直线交点为H，过P点做直线交定直线于D，设由极坐标可设

P(ρ,θ)为轨迹上任意一点。即ρ=OP，|DP|=|HO|+ρcosθ，又变形得。这就是圆锥曲线的极坐标方程，其中e是离心率，焦点位于极点。极轴是曲线对称轴。因为同时注意p是曲线顶点到定直线的距离，其中0＜e＜1是椭圆，e=1是抛物线，e＞1是双曲线。不过对双曲线要说明一下，当把平面直角坐标系转化到极坐标中还有是因为平面直角坐标系分为左右两支双曲线。

到这里关于平面直角坐标与极坐标转化的圆锥曲线问题探讨的拙文就结束了，对圆锥曲线的直角坐标转化极坐标晕眩是比较复杂的但是只要注意就可以得到最后的结果，当然直接推导得出的结果就非常的简洁。希望大家读到这篇文章，能对大家教学或者学习启发，谢谢！