基于PERT的工程项目进度研究

阳泽宇 蹇朱韬宇 李翊禹 周昌智

摘 要：施工项目具有投资较大，对专业人员、各种原材料和机械设备的需求比较大的特点。建设项目规模越大，工程中各项工作内容、持续时间、衔接关系等纵向、横向关系也越来越复杂。怎样做到尽可能地缩短工期，把项目做到又快又好，是每个施工人员的愿望。如果耽误时间会造成很大的损失，这种损失不仅仅是金钱上的损失，有时为了赶工期，会造成工程质量的下降，继而引发安全性的问题。[1]怎样运用科学的方法对建设项目进度风险进行分析，然后加以控制，使项目计划在管控制中进行是一个重要的问题。因此引入PERT技术对于工程项目进行进度分析有着重大的意义。

关键词：PERT技术;进度控制;工作持续时间

1 绪论

PERT（Program/Project Evaluation and Review Technique）即计划评审技术。常见的网络计划方法有PERT和CPM两种，它们均产生于上世纪50年代。CPM主要用于有着过往经验的项目的开发，PERT主要用于新项目的开发，上世纪50年代美国海军“北极星”导弹计划在应用了PERT技术之后，计划缩短了2年。1962年钱学森将PERT技术带回国内，1965年由华罗庚加以推广，命名为“统筹法”。因为PERT和CPM有相同的目标应用，又有很多相同的术语，可以合并为一种方法，“统筹法”即是PERT技术和CPM技术的统称，国外称为PERT/CPM。

工程项目进度是指工程项目实施的进展情况，在工程项目实施过程中要消耗时间（工期）、劳动力、材料、成本等才能完成项目任务。[2]在现代项目管理中将项目的任务、工期、成本和资源有机地结合起来形成了一个综合的指标以此来作为工程进度的综合含义。但是在在实际工作中对于工程量、资源消耗等条件，无法用一个定量的指标来将他们进行分析研究，进度控制大多还是根据传统意义上的工期控制。

2 研究方法

开展工程项目进度分析工作的第一步是要在项目的网络图中找出所有的路徑，根据每条线路工作持续时间的长短及发生概率来确定关键路径以及工作持续时间的分布。

根据工程的性质，假设在不同条件下，工程完成所需要的时间。工程项目在最优条件下完工所需要的时间为a，工程项目在最差条件下完工所需要的时间为b，工程项目在一般条件下完工所需要的时间为m。引入如下公式：tij=（a+4m+b）/6、sij2=（b-a）2/36。（tij表示工作持续时间的均值也可以称作是期望值，σij2代表最优和最差条件下工作持续时间的方差。工程持续时间的期望值表示完成该工程所需时间的多少。方差表示该工程在期望的时间内完成的概率，方差越小表示在期望时间内完成的概率越大，方差越大表示在期望时间内完成的概率越小。）在计算出每项工作的期望值和方差之后，按照已经计算出来的线路，对线路上不同工作的期望值和方差分别相加，所得到期望值最大的路线即为关键线路。如果时间足够多的话，每一个工作的持续时间对整个项目工期影响足够小时，由中心极限定理，其均值和方差分别为关键线路上各个工作持续时间期望值之和、方差之和。

3 算例分析

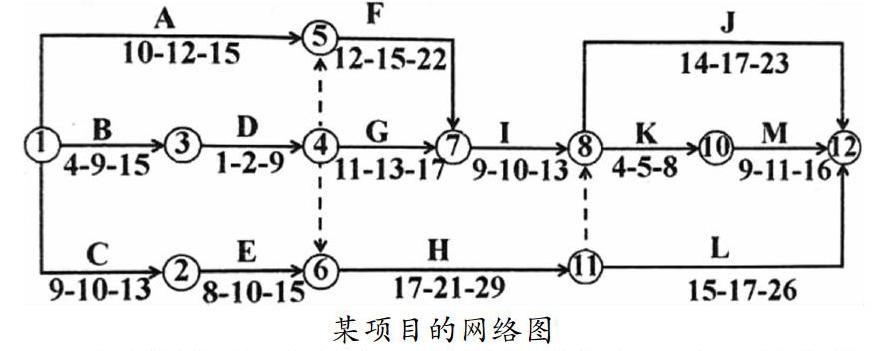
假设某项目的网络图以及各工作的持续时间如下图所示。

某项目的网络图

通过分析可以发现，该项目网络图共有12条工作路线。分别是：AFIKM、AFIJ、BDFIKM、BDFIJ、BDGIKM、BDGIJ、BDHL、BDHKM、BDHJ、CEHL、CEHKM、CEHJ。根据给出的方法，应该先计算出各个工作的工作持续时间的期望值和方差，对计算出来的结果再根据工作线路进行累加。计算出各条工作线路的期望值和方差。

各工作持续时间期望值计算：工作A持续时间期望值t（A）=（10+12*4+15）/6=12.17，工作B持续时间期望值t（B）=（4+9*4+15）/6=9.17，以此类推可以计算出C工作期望值为10.33、D工作期望值为3、E工作期望值为10.5、F工作期望值为15.67、G工作期望值为13.33、H工作的期望值为21.67、I工作期望值为10.33、J工作期望值为17.5、K工作期望值为533、L工作期望值为18.17、M工作期望值为11.5。

各工作持续时间方差计算：工作A持续时间方差σA2=（15-10）2/36=0.69，工作B持续时间方差σB2=（15-4）2/36=3.361，以此类推C工作方差为0.444、D工作方差为1.778、E工作方差为1.361、F工作方差为2.778、G工作方差为1、H工作方差为4、I工作方差为0.444、J工作方差为2.25、K工作方差为0.444、L工作方差为3.361、M工作方差为1.361。

将所得到的各个工作的期望值和方差带入相关工作线路，得到线路AFIKM期望值为55.方差为5.721。线路AFIJ期望值为55.67.方差为6.166。线路BDFIKM期望值为55.方差为10.166。线路BDFIJ期望值为55.67.方差为10.611。线路BDGIKM期望值为52.66.方差为8.388。线路BDGIJ期望值为53.33.方差为8.833。线路BDHL期望值为52.01.方差为125。线路BDHKM期望值为50.67.方差为10.944。线路BDHJ期望值为51.34.方差为11.389。线路CEHL期望值为60.67.方差为9.166。线路CEHKM期望值为59.33.方差为761。线路CEHJ期望值为60.方差为8.055。

由计算结果可以发现，所有工作线路中期望值最高的线路为CEHL，期望值为60.67，方差为3.028所以线路CEHL为该网络图中的关键线路。该工作项目的工期服从（60.67，30282）的正态分布。

倘若业主方要求该工作项目要在56天之内完工，那么该项目的完工概率为：

P（T≤60）=P[λ≤（56-60.67）/3.028]=P（λ≤-1.5422）=0.0618。

在統计学上当某个事件发生概率在95%以上时，那么这个时间是大概率可以发生的，可以尝试计算各条工作线路在95%完工概率的情况下需要的工作天数。通过查阅正态分布表，我们可以得到当P=95%时，l0=1.6449。利用公式T=TE+16449*s即可算出。（TE：工作线路的完工天数期望值，s：工作线路在最优条件以及最差条件下工作持续时间的标准差）

T（AFIKM）=55+1.6449*2.392=58.93，T（AFIJ）=55.67+1.6449*2.483=59.75，以此类推T（BDFIKM）=60.24，T（BDFIJ）=61.03，T（BDGIKM）=57.42，T（BDGIJ）=58.22，T（BDHL）=57.83，T（BDHKM）=56.11，T（BDHJ）=56.89，T（CEHL）=65.65，T（CEHKM）=63.87，T（CEHJ）=64.67。

由此可知项目最有把握（P=95%）在65.65天完成。

4 结语

应用PERT技术将整个工程项目予以分解和重新组合，然后建立起相应的PERT网络模型。借助这个模型将传统的依照顺序进行施工的方式转变为多项工作之间平行或者交叉的工作关系。从而发挥多项工作同时进行的优势，在原有基础上大大提高工作效率。PERT与传统项目管理方式最大的优势就是在没有过往类似工作经验的情况下，可以比较容易的估算出完成工程项目所需要的持续时间。在充分的考虑了工程项目在有利、不利、一般工作条件下的完成所需时间，然后通过科学的加权平均，这样得出来的数据更加的科学、可靠。根据对工程项目工期的估算结果，可以计算出在一定时间范围以内完工的概率，方便在不同的工程方案中做出决策。PERT技术要想在工程项目中真正发挥出它的作用还需要业主方积极参与协调配合不同工作项目之间的关系，使他们尽可能处于平行工作状态。本文从进度控制最基本的因素出发，运用PERT技术对工程项目进行分析，得出各工作的期望工期和方差，从中选出了最优的工作方案，可以清楚的看见PERT技术对于工程项目管理的可行性和有效性。对于我国这样一个基建大国来说，采用PERT技术可以对工程项目的人力、物力、财力资源进行有效的分配，从而提高资源的利用率。更好的控制项目进度，保证项目按时按量的完成。PERT技术值得在我国工程界大力推广。

参考文献：

[1]银花.建设工程监理目标控制与应用[D].天津大学，2008.

[2]成虎.工程项目管理[M].高等教育出版社，2004：508.