带缘板阻尼结构转子叶片振动特性的影响参数分析
2019-10-19张大义付检伟
张大义,杨 诚,夏 颖,付检伟,洪 杰
(1.北京航空航天大学 能源与动力工程学院,北京 100191;2.先进航空发动机协同创新中心,北京 100191)
在现代航空燃气涡轮发动机中,因振动带来的叶片高周疲劳断裂问题是影响发动机可靠性的关键问题之一[1]。对于叶片的振动抑制而言,干摩擦阻尼结构由于其减振效果明显、结构简单及可靠性高等特点,在航空发动机中得以广泛应用。常见干摩擦阻尼结构形式包括凸肩、叶冠和缘板阻尼结构等[2-3]。其中,缘板阻尼结构(Under Platform Damper,UPD)因附加离心负荷小、对气动性能无不利影响等优点,被广泛应用于风扇叶片和涡轮叶片的减振设计[4],如CFM56-3、太行等发动机的风扇叶片,以及JT9D、CF6、RB211、BR715、АЛ-31Ф、РД33等发动机的高压涡轮叶片[5-6]。
在微观尺度对缘板与阻尼块接触表面的力学特性进行定量表征是研究缘板阻尼结构的首要工作。早期研究多采用宏观滑移模型,其假设接触面上的变形和压力都是均匀分布的,接触面整体同时进入黏滞或滑移状态。代表性工作包括:Yang等[7-8]提出的耦合双接触面模型,Sanliturk等[9]建立的小自由度理论模型,郝燕平等[10-11]采用的B-G简化模型。与宏观滑移模型相比,微动滑移模型则可以更好地刻画接触表面之间存在的局部滑移现象,进而更准确地预测接触面力学特性[12-13]。代表性工作如Sanliturk等[14]采用多个接触对并联形式建立微动滑移模型,漆文凯等[15]采用整体局部一体化模型分析缘板阻尼结构,Panning等[16]采用微动滑移模型对比分析楔形缘板阻尼结构与圆柱形缘板阻尼结构的减振效果。Petrov[17]采用自行开发的干摩擦非线性振动响应求解程序,分析得到了不同结构形式阻尼结构的减振效果。
在宏观尺度研究叶片振动特性的关键影响参数及影响规律是工程应用中的关注点,大量文献基于宏观滑移模型开展了相关研究,如:郝燕平等[18]采用动柔度法计算分析了缘板阻尼器切向刚度和摩擦面的摩擦因数对叶片响应的影响,吴向宇等[19]采用轨迹跟踪法计算分析了阻尼块质量的影响规律,李琳等[20]采用B-G集中参数模型分析了缘板阻尼结构对宽频多阶次激励的减振效果。上述研究均采用宏观滑移模型,因此无法考虑缘板-阻尼块复杂接触状态的影响,进而限制了所获得规律的准确性。
借鉴上述工作,作者在文献[21]中针对缘板阻尼结构建立了分布式摩擦力学模型,并建立了带有分布式摩擦高维度叶片的振动响应求解方法。本文在其基础上,将微动滑移模型应用于高维度叶片模型的振动特性分析,进一步研究正压力、质量、摩擦因数等缘板阻尼结构关键参数对叶片振动特性的影响规律,为工程设计提供亟需的数据参考。
1 理论模型与求解方法
缘板阻尼结构简图及工作原理如图1所示。在工作状态,缘板阻尼块由于离心载荷作用,压紧在两个相邻叶片缘板下表面。当叶片发生振动时,缘板与阻尼块之间发生相对运动,接触面干摩擦效应消耗叶片振动的部分能量。
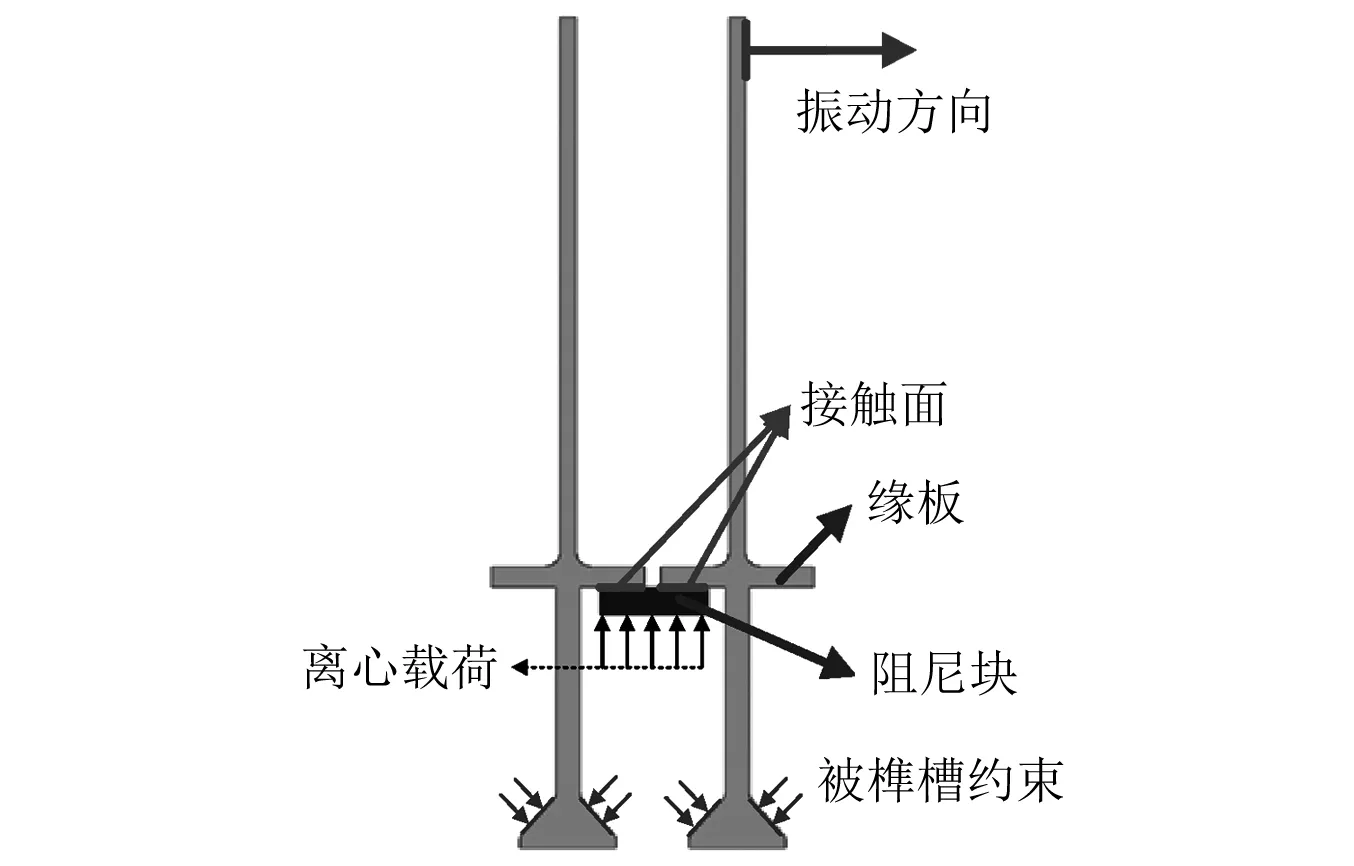
图1 缘板阻尼结构原理图Fig.1 The sketch of UPD
1.1 微分形式摩擦力
迟滞摩擦模型被广泛用于确定接触点对的切向摩擦力。当正压力不变时,接触点对的沿接触面切向摩擦力的表达式为[22]
(1)
式中:f为摩擦力;kt为切向接触刚度;μ为摩擦因数;N为接触面的法向压力;gt为接触点对沿接触面切向方向的相对位移;sgn(·)为符号函数,表征摩擦力始终与相对运动的方向相反。
大多文献中采用式(1)所示的积分形式的摩擦力学模型。其局限性在于式(1)仅适用于正压力不变的情况;当正压力变化时,需要在每一个时间步内,通过复杂计算来判断接触面的接触状态(黏滞,分离或滑移)。本文计算分析中采用微分形式摩擦力,摩擦力对时间的导数为

(2)
式中:H(·)为Heaviside函数,满足
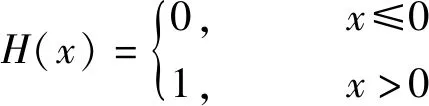
(3)
将摩擦力写成如式(2)所示,可以将摩擦力视为附加的自由度直接参与到动力方程的求解中,而不必考虑摩擦力对原有动力学方程复杂的约束条件,简化了摩擦力的求解过程。微分形式的摩擦力学模型对于宏观滑移模型和微观滑移模型均适用。
1.2 非线性摩擦力的等效刚度和等效阻尼
阻尼块与叶片缘板接触表面的非线性摩擦力会改变叶片的刚度和阻尼,进而导致其动力学特性如共振频率、振动幅值等发生变化。将非线性摩擦力近似表达为如式(4)所示的位移和速度的线性组合
(4)
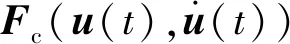
在不同时刻式(4)的左端项和右端项的相对误差是不同的。当Kad和Cad选取合适的值时,可以保证在一个振动周期内,此近似关系的相对误差最小。采用最小二乘法得到近似关系式(5)的误差函数为
(5)
根据误差函数取极小值推导可得非线性摩擦力的等效刚度和等效阻尼,如式(6)~式(7)所示。
(6)
(7)
等效刚度和等效阻尼可以近似地定量反映出接触面摩擦力对叶片刚度和阻尼带来的改变,一定程度上决定了其对叶片动力学特性的影响,其中,等效刚度主要影响叶片共振频率,而等效阻尼主要影响叶片在各种不同激励条件下的响应幅值。上述公式给出的等效刚度和等效阻尼的表达式,对于宏观滑移模型和微观滑移模型均适用。
1.3 分布式接触摩擦模型
微分形式的分布式接触摩擦模型是Zhang等提出的一种微动滑移模型,如图2所示。通过多对接触点对的形式,可以考虑接触面上部分接触点发生滑移,而其他接触点保持黏滞状态的情况。
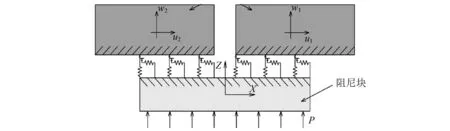
图2 分布式接触摩擦模型示意图Fig.2 A sketch of distributed contact model
实际工作时,接触面的法向压力分布是不均匀的。当接触的特征时间远大于弹性波在接触面上的传播时间时,该系统在运动过程的每一个时刻都处在平衡状态。由此,将惯性力视作外力采用静力学计算得到的接触面压力分布与接触面发生相对运动时的压力分布是相同的,该条件称为接触应力的准静态条件。根据Zhang等的推导结论,缘板阻尼结构满足准静态条件。因此,通过静力学计算来确定缘板阻尼结构接触面的压力分布形式。
缘板阻尼器可以根据图2等效为带分布式接触面的单自由度振子模型。则根据式(2),计算缘板阻尼器运动的方程为
(8)
式中:x为阻尼块沿接触面切向的位移;m为阻尼块的质量;yi为叶片缘板上第i个接触点的位移;fi和Ni分别为接触面上第i个接触点上的摩擦力和正压力;kit表示第i个接触点的切向接触刚度。假设缘板各节点的运动状态已知,根据静力学求得的压力Ni,通过对式(8)进行数值积分即可求解缘板阻尼结构接触面的分布式摩擦力fi。
2 关键参数对等效刚度与等效阻尼的影响
如前所述,缘板-阻尼块接触面之间的摩擦力会改变叶片的刚度和阻尼,进而影响其动力学特性。通过对摩擦力等效刚度和等效阻尼的分析,可以更为深入地认识缘板阻尼结构对叶片动力学特性的影响机制。因此本节采用宏观滑移模型定性分析缘板阻尼结构关键参数对摩擦力等效刚度和等效阻尼的影响规律,进而为第“3”节结果的解释提供依据。
根据减振原理,将缘板阻尼结构简化为压紧在振动基础上的自由振子,如图3所示。一个质量为m的质量块在正压力N的作用下压紧在刚性皮带上。其中,刚性皮带做简谐振动,模拟叶片的缘板;而质量块与皮带间仅通过摩擦力相互作用,模拟阻尼块。
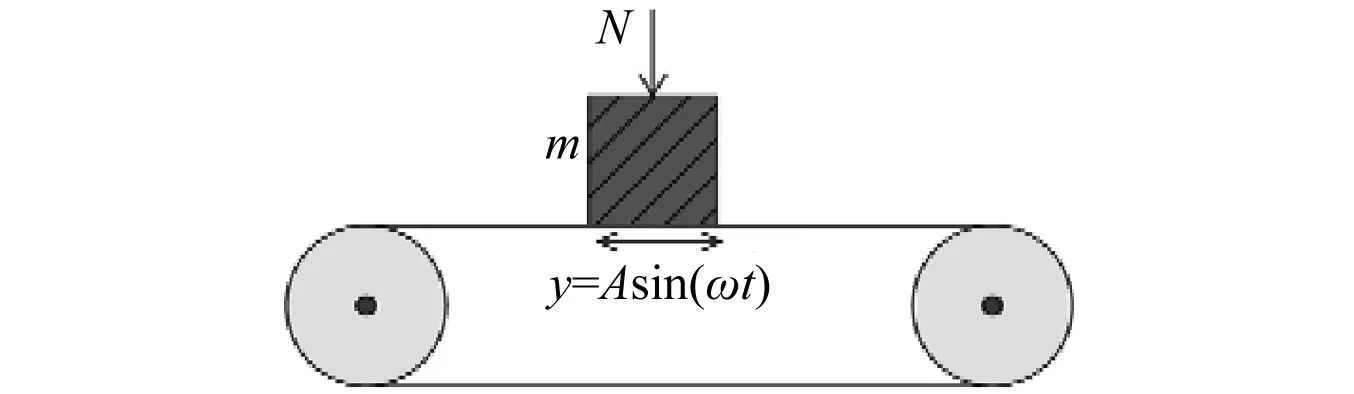
图3 缘板阻尼结构的简化模型Fig.3 A simplified model for UPD
根据“1.1”节所述的微分形式的摩擦力学模型,计算得到摩擦力时域内的曲线和迟滞回线,如图4所示。迟滞回线对角线的连线的斜率反映等效刚度大小,而迟滞回线围成的面积反映摩擦力的阻尼大小,该面积越大代表耗散能量越多。根据“1.2”节所述,可计算出摩擦力的等效刚度和等效阻尼。

图4 摩擦力曲线Fig.4 Friction force
2.1 工作正压力
图5中给出了正压力对摩擦力的等效刚度和等效阻尼的影响规律。结果表明:①随着正压力增加,摩擦力等效刚度先非线性增加而后趋于某一稳定值,其原因在于随着正压力增加,振子的滑移位移减小,当正压力到某值时,振子与皮带间处于黏滞状态,此时等效刚度不再变化,即为接触面切向刚度;②随着正压力增加,摩擦力等效阻尼先迅速增加后缓慢减小,当正压力达到250 N时,其等效阻尼达到最大值。其原因在于,随着正压力增加,摩擦力增加而滑移位移减小,由于摩擦消耗的能量为摩擦力与滑移位移的乘积,当正压力较小时摩擦力增加占主导因素,表现为等效阻尼增加,当正压力较大时,滑移位移占主导因素,表现为等效阻尼减小。
最佳阻尼效果对应的正压力称为“最佳压紧力”。
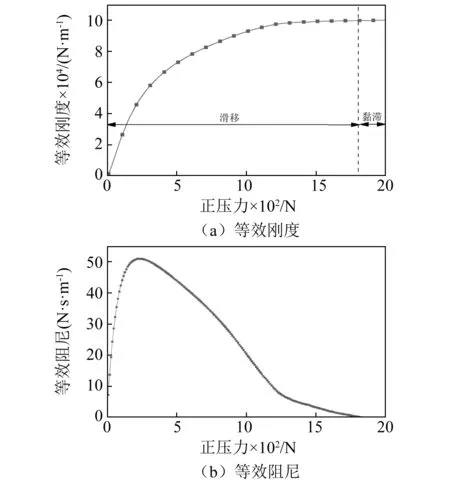
图5 正压力的影响规律Fig.5 The influence of normal load
2.2 质 量
摩擦力的等效刚度和等效阻尼在不同相对质量下,随正压力的变化规律如图6所示。结果表明:①随阻尼块质量增加,摩擦力等效刚度减小,达到黏滞状态的正压力增加,其原因在于正压力一定时,阻尼块的质量越大,惯性越大,越难跟随缘板一起振动,与缘板之间的相对位移越大,进而减小了迟滞回线对角线的连线的斜率,等效刚度越小,越难进入黏滞状态;②随阻尼块质量增加,最佳压紧力增加,最佳压紧力对应的等效阻尼先增加后基本不变,其原因在于正压力一定时,随着质量增加,阻尼块的相对位移增加,摩擦力增加,等效阻尼也增加,当阻尼块质量增加到一定程度时,阻尼块相对位移基本不变,等效阻尼也基本不变;③随阻尼块质量增加,具有良好阻尼效果对应的压紧力范围越宽,其原因在于阻尼块质量越大,自身惯性越大,越不易进入黏滞状态,从而可以在较宽的压紧力范围内产生较大的阻尼。
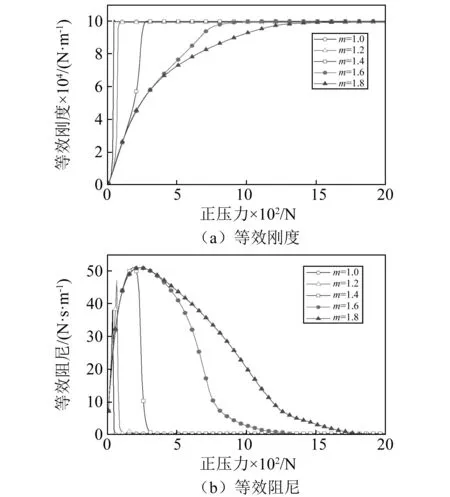
图6 质量的影响规律Fig.6 The influence of mass
2.3 摩擦因数
在不同摩擦因数下,摩擦力的等效刚度和等效阻尼随正压力的变化规律,如图7所示。结果表明:①随摩擦因数增加,摩擦力的等效刚度增加,达到黏滞状态的正压力减小,其原因在于正压力不变时,随摩擦因数增加,摩擦力变大,更易进入黏滞状态;②随摩擦因数增加,最佳压紧力减小;最佳压紧力对应的等效阻尼与摩擦因数基本无关。
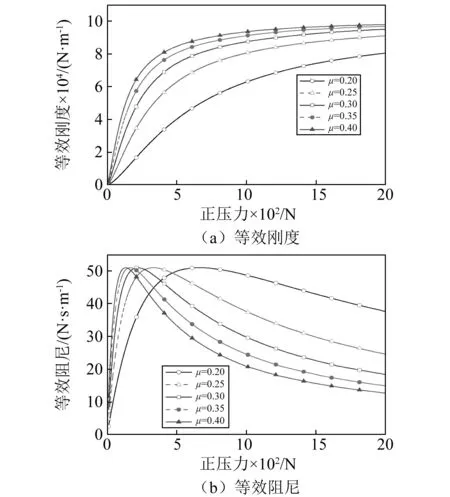
图7 摩擦因数的影响规律Fig.7 The influence of friction coefficient
3 带缘板阻尼结构叶片的振动特性
本节进一步将有限元法和“1.3”节所述的分布式接触摩擦模型相结合,建立缘板阻尼结构-叶片系统的非线性动力学模型,基于作者已建立的带有缘板阻尼结构的叶片振动响应求解方法,研究缘板阻尼结构关键参数对叶片振动特性的影响规律,并结合等效刚度和等效阻尼概念分析其影响的内在机制。
在实际工作中,轮盘上的叶片为周期对称结构,为了减小计算规模,在计算中通过引入周期性边界条件,通过计算单个叶片的动力学响应获得所有叶片的响应。叶片周期性边界条件可以表示为接触面上对应接触点的摩擦力相等,如式(9)所示。
(9)
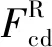
图8为带缘板阻尼结构的平板叶片有限元模型,叶片榫头施加位移全约束,叶身施加均布的简谐激振力。系统的振动方程[23]如式(10)所示
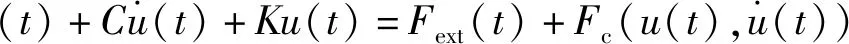
(10)
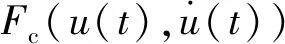
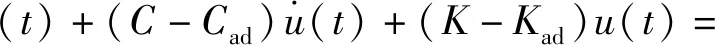
Fext(t)+Fc0
(11)
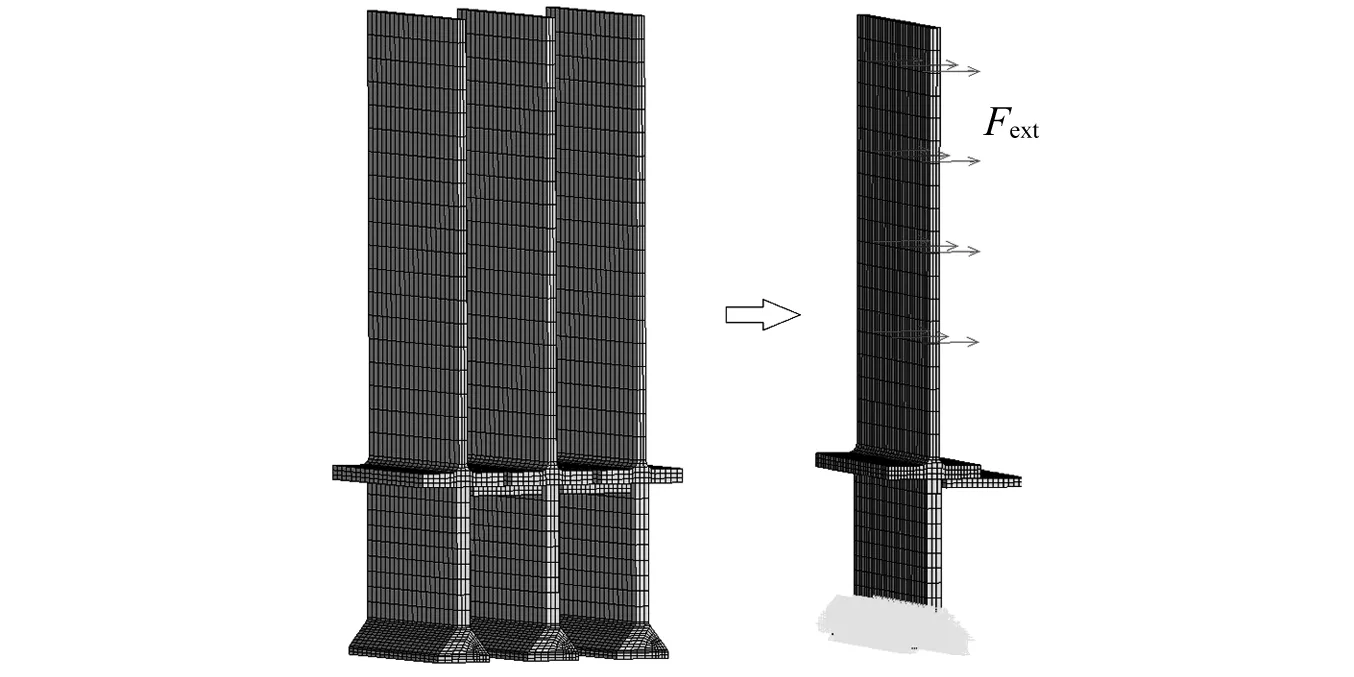
图8 带有缘板阻尼结构的叶片的有限元模型Fig.8 Finite element model of blades with UPD
采用如图9所示的叶片振动响应求解流程,通过迭代求解不同参数下叶片的振动响应,进而得出不同参数对叶片的振动特性的影响规律。工程设计中,所关心的叶片振动特性包括两个方面,一个是叶片的共振频率,另一个是叶片在等幅激振力下的稳态响应幅值。
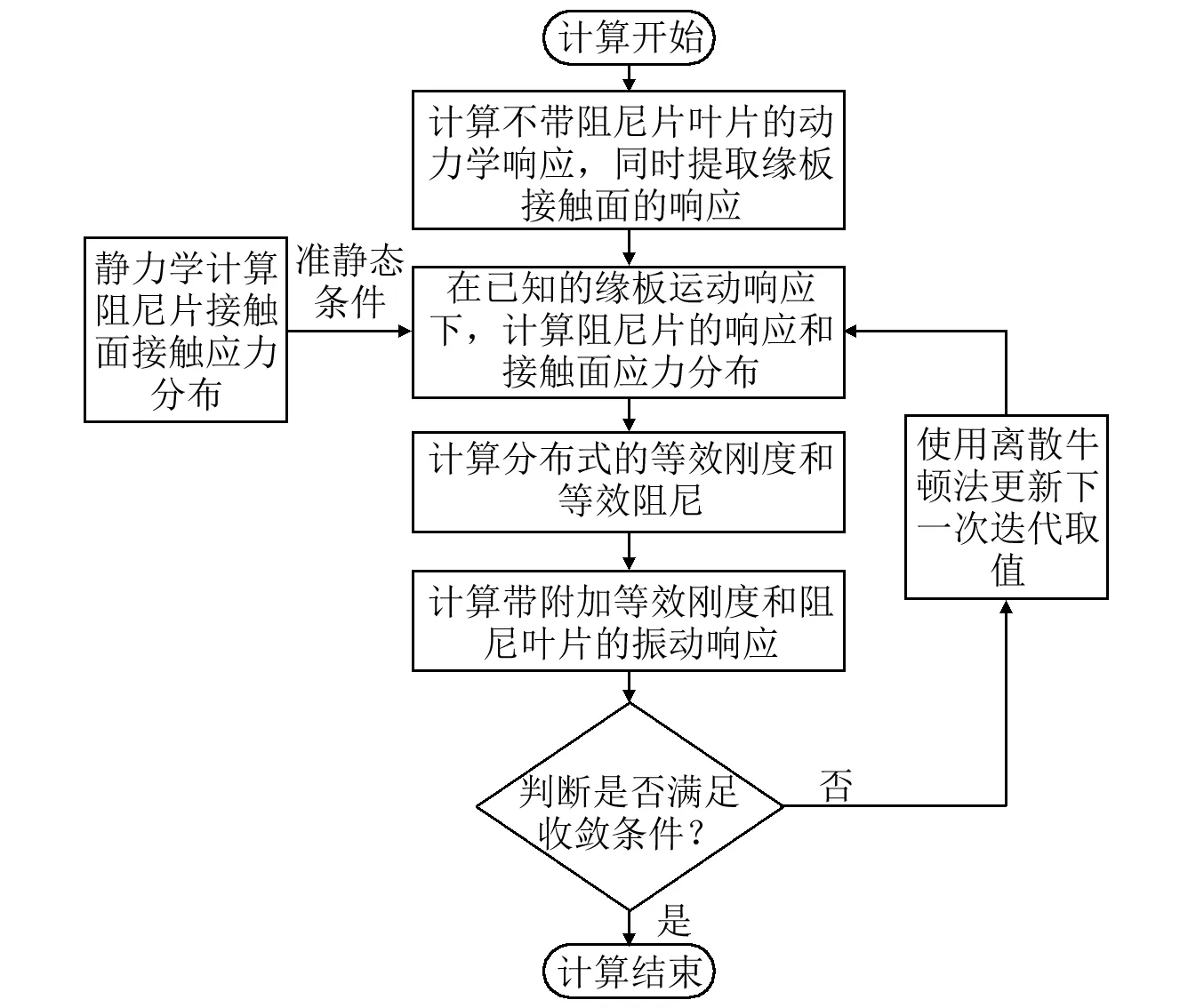
图9 叶片振动响应求解流程 Fig.9 Solving process of the vibration response of the blade
3.1 工作正压力
数值求解获得叶片在不同频率的等幅激励下,不同正压力对应的无量纲振动响应幅值,如图10所示。无量纲振动响应幅值定义为振动响应幅值与不带缘板阻尼结构的叶片发生共振时的响应幅值之间的比值。结果表明,随阻尼块所受正压力增加,叶片的一阶共振频率逐渐升高,叶片的稳态响应峰值先迅速减小后缓慢增大。其原因在于随着正压力的增加,等效刚度逐渐增加而等效阻尼先迅速增大后缓慢减小。因此,为了保证缘板阻尼结构的最佳减振效果,缘板阻尼结构工作时的正压力应选为最佳压紧力或略大于最佳压紧力。
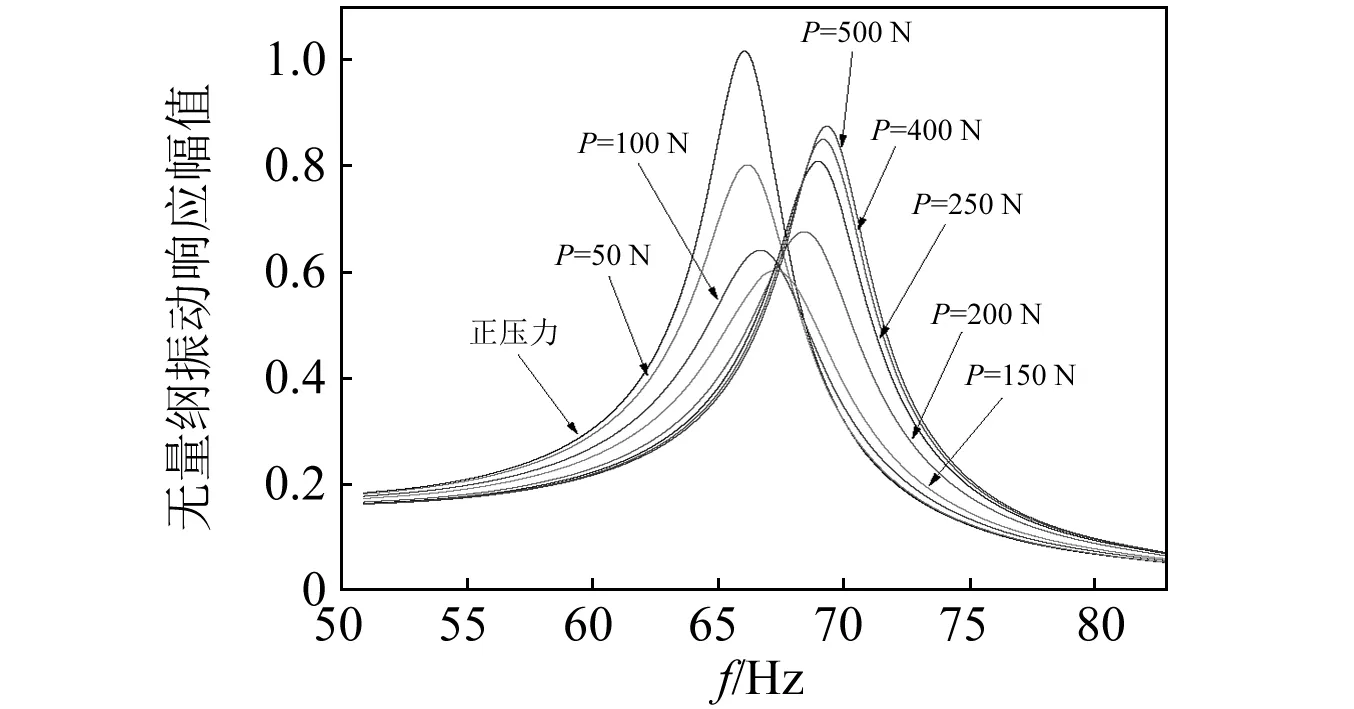
图10 不同正压力条件下系统的无量纲振动响应幅值Fig.10 Comparison of the curves of normalized frequency response function under different normal load
3.2 质 量
通过数值计算获得了阻尼块的相对质量对叶片振动特性的影响规律,如图11所示。图11(a)为叶片一阶共振频率的变化规律,而图11(b)为无量纲振动响应峰值的变化规律。可见,缘板阻尼结构最佳减振效果可以使叶片振动响应下降78%。
由图11可知,阻尼块的质量对叶片振动特性的影响规律如下:①随阻尼块质量增加,叶片振动频率减小,其原因在于等效刚度随着质量的增加而减小;②随阻尼块质量增加,最佳压紧力增加,最佳压紧力下的阻尼效果随着质量的增大先增加后趋于不变;③减振效果大于75%对应的正压力范围随着质量的增大而增加。
因此,在一定范围内增加阻尼块的质量可以提高最佳压紧力对应的阻尼效果;当正压力在较大的范围变化时,选用较大质量的阻尼块可以获得较好减振效果。由于阻尼块的正压力也与阻尼块的质量相关,阻尼块的质量应根据工作转速综合考虑。
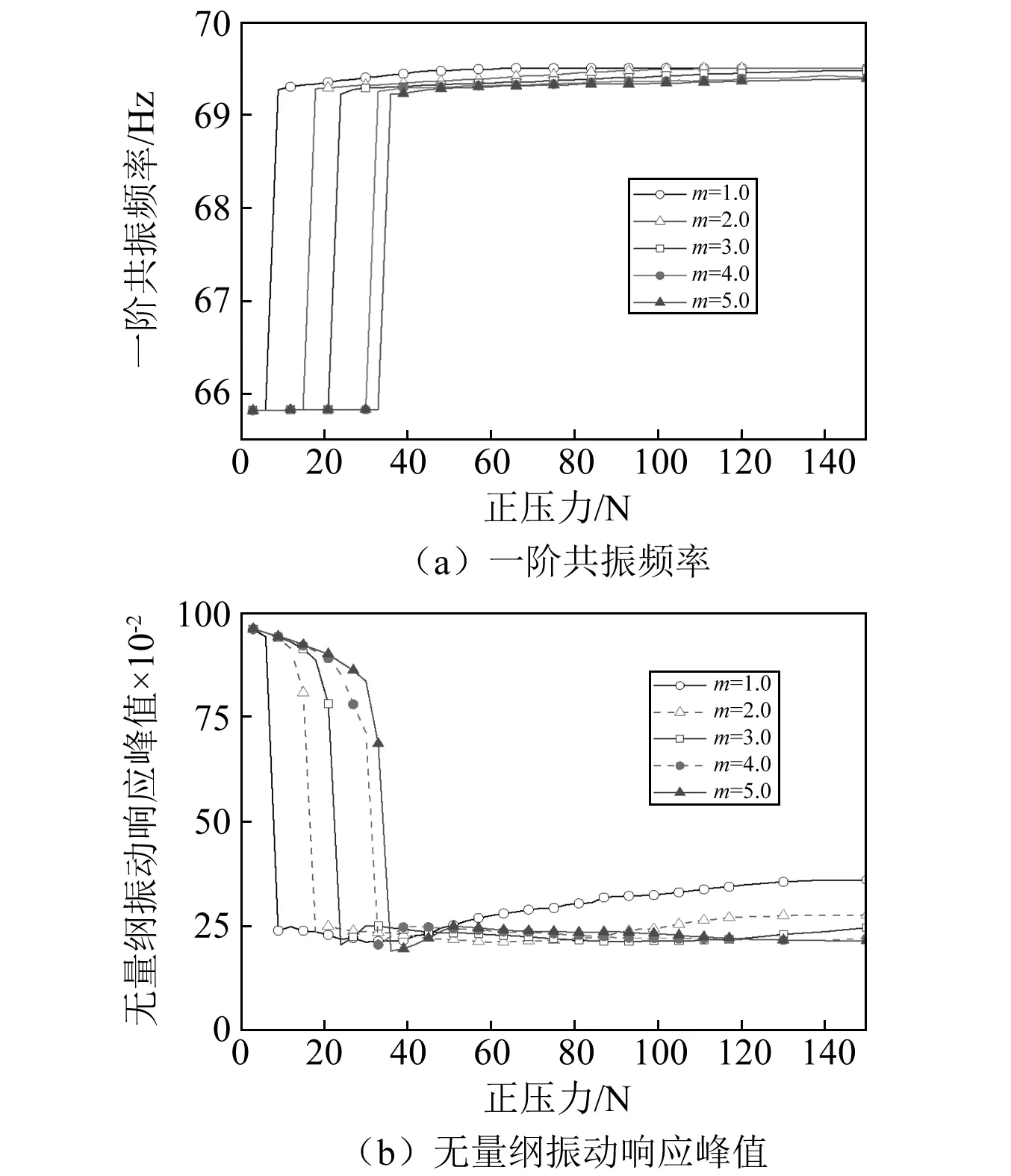
图11 质量对叶片振动特性的影响规律Fig.11 The influence of mass on the vibration characteristics of the blade
3.3 摩擦因数
通过数值计算获得了接触面的摩擦因数对叶片振动特性的影响规律,如图12所示。由图12可知:①随摩擦因数增加,叶片的共振频率增加,其原因在于等效刚度随摩擦因数增加而增加;②随摩擦因数增加,最佳压紧力减小,最佳压紧力下的阻尼效果基本不变。③减振效果大于75%对应的正压力范围随着摩擦因数的增大基本不变。
因此,增大摩擦因数并不能提高最佳压紧力状态下的减振效果,也不能增加具有良好减振效果时正压力的范围。由于缘板阻尼结构在工作过程中摩擦因数会逐渐减小,应选择较大的正压力以保证缘板阻尼结构始终具有较好减振效果。
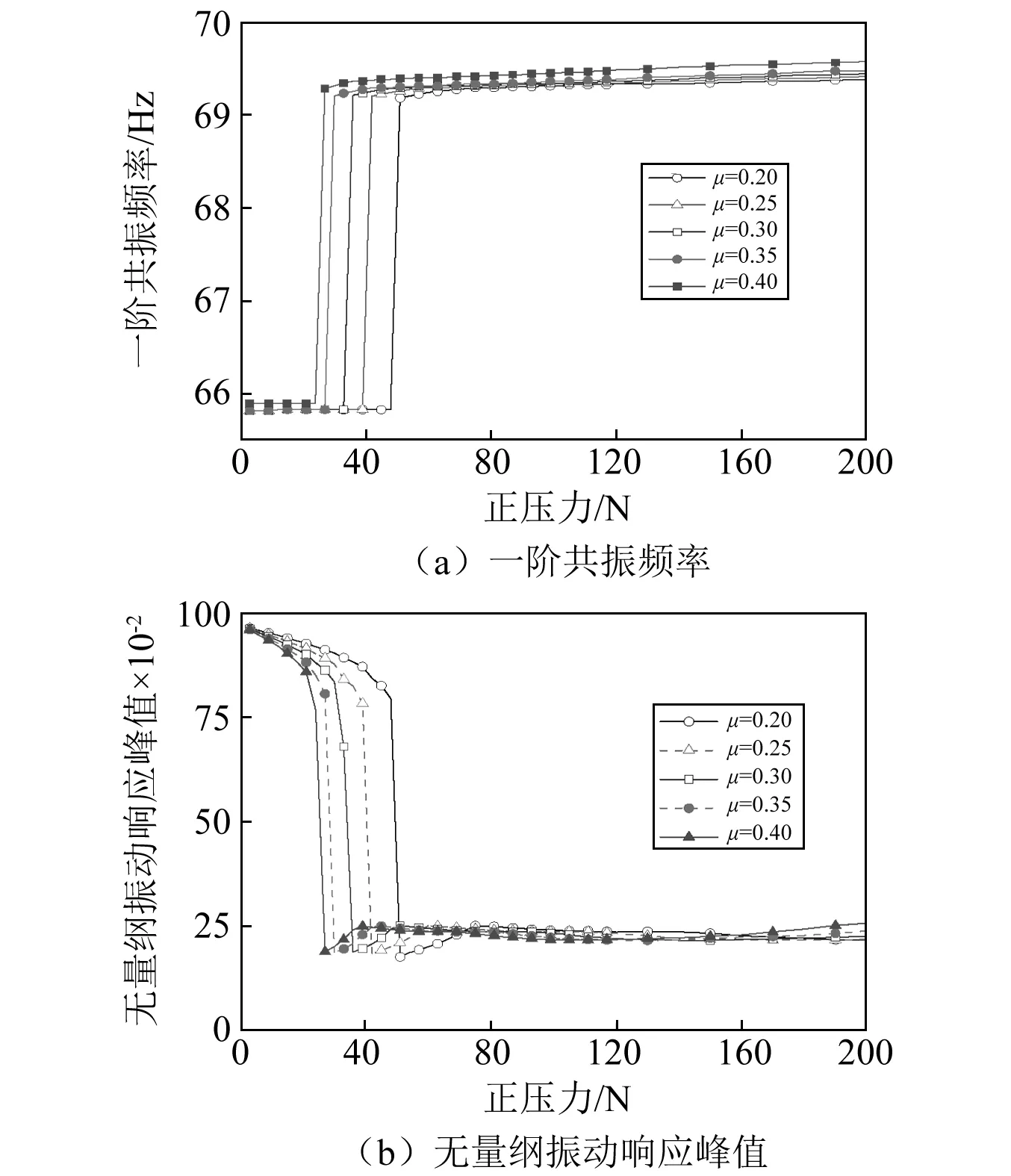
图12 摩擦因数对叶片振动特性的影响规律Fig.12 The influence of friction coefficient on the vibration characteristics of the blade
4 结 论
本文首先通过简化模型分析了缘板阻尼结构接触对刚度和阻尼的影响;然后以带缘板阻尼结构的平板叶片为研究对象,采用分布式接触摩擦力学模型,分析了缘板阻尼结构关键参数对叶片振动特性的影响规律,得出以下主要结论:
(1)存在最佳压紧力使得缘板阻尼结构的减振效果最好;通过优化阻尼块质量,可使叶片振动响应幅值下降78%。
(2)缘板阻尼结构工作时的正压力应选为最佳压紧力或略大于最佳压紧力;最佳压紧力随着阻尼块质量的增加而增大,随着摩擦因数的增大而减小;最佳压紧力对应的阻尼效果随着质量的增加先增大后基本不变,且与摩擦因数的大小基本无关。
(3)具有良好减振效果的正压力范围随着质量的增大而增大,且与摩擦因数的大小基本无关,因此在设计中可适当增大阻尼结构质量,以提高减振稳健性。
