汽车发动机悬置安装点最佳位置的优化研究
2019-10-19王田修王晨光杨洁丹王晓蒙
王田修,王晨光,杨洁丹,王晓蒙,黄 煜
(1.上汽通用五菱汽车股份有限公司,广西 柳州 545007;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
动力总成是汽车的主要激励源,降低动力总成传递到车身的振动能量对于降低整车振动噪声有很大帮助[1]。近年来国内外学者针对动力总成悬置的优化问题进行了许多研究[2]。能量解耦法、扭矩轴(Torque Roll Axis,TRA)解耦法应用十分广泛,采用能量解耦的方法可以使系统在各个方向上的解耦率达到最优,便于对振动传递的抑制[3],对动力总成刚体振动模态的频率配置和解耦布置是动力总成悬置系统设计的基本任务[4]。同时,还有许多学者针对传递振动力、传递能量以及力传递率最小对悬置进行了优化[5]。优化的目标函数定义多种多样,目的都是通过合理选择悬置的刚度参数,使动力总成传递到车身的振动最小,来降低车内的噪声大小。但是,这些优化往往都是在整车设计定型后进行的,优化的对象只是刚度,对于悬置系统的其他参数鲜有涉及。以传递能量最小为目标的优化还要考虑车架的弹性,即悬置点之间导纳函数。悬置点安装位置会影响这一参数,有必要对悬置点安装位置进行优化分析。
本文以某直列四缸发动机三橡胶悬置样车为例,以传递到车身功率流最小为目标,建立了考虑车身弹性的动力总成、悬置和车身的十五自由度耦合模型,根据实验测得的悬置点间导纳函数以及通过实验测试辨识得到的动力总成质心等效激励力,计算了悬置到车身传递的功率流大小。分析了悬置点之间导纳函数改变对输出功率流影响的灵敏度,找出最能影响输出功率流大小的导纳函数组,确定重点优化研究的悬置点位置,在完整车身有限元模型中计算不同悬置点安装位置对悬置点之间导纳函数的影响,进而确定最有利于减小振动传递的悬置点安装位置,使悬置传递到车身的功率流最小,并通过计算系统固有频率、车身悬置点支反力和TRA解耦率验证悬置安装位置的优化结果。
1 系统动力学耦合模型
对悬置进行优化,首先要建立动力总成、悬置和车身的动力学耦合模型[6-8],在模型的建立过程中,以动力总成质心坐标系为标准,O-XYZ为与动力总成质心坐标系平行的广义坐标系,而UVW坐标系为各个悬置安装位置与方向所决定的局部坐标系,分别对应左悬置、右悬置和后悬置,如图1所示。

图1 动力总成、悬置、车身简化模型Fig.1 Simplified model of an engine-mount-body system
在简化模型中,动力总成被简化成包含3个平动3个转动的六自由度刚体,每个悬置与弹性的车身连接的节点具有3个平动自由度,整个简化系统可以看做为十五自由度的模型。
根据拉格朗日方程,系统的振动微分方程为
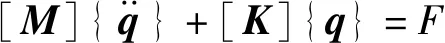
(1)
式中:{q}={q0,q1}T分别为动力总成质心和3个悬置对应的广义坐标;[M]为系统质量矩阵;[K]为系统刚度矩阵;F为动力总成质心等效激励力。
系统质量矩阵表达式为
(2)

系统刚度矩阵表达式为
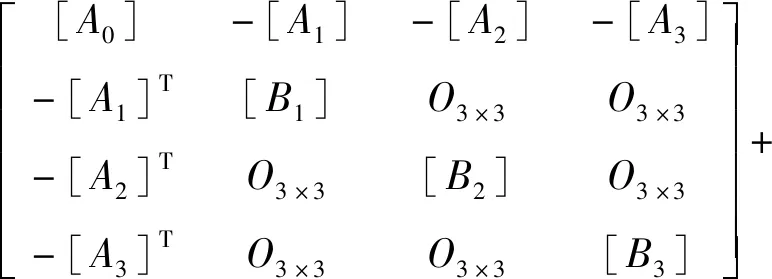
(3)
式中:

得到了动力总成悬置系统质量矩阵、刚度矩阵和激励力信息后,可以通过激励力计算车身悬置点的稳态振动响应,动力总成悬置系统传递到车身的功率流表达式可以写出,它是由支反力和悬置点的速度在稳态状态下相乘得到的。3个悬置在9个方向传递到车身的稳态功率流为
(4)
式中:Q1为悬置点的稳态振动响应;V1为车身悬置点稳态速度响应;F1为车身悬置点支反力的稳态响应。
2 实验分析
虽然系统质量矩阵与刚度矩阵的表达式已经得出,但是计算传递到车身的总功率流还需要系统的激励和悬置点之间的导纳函数[H],可以通过实验测试得到。
2.1 动力总成激励力辨识实验
要求得整个系统的振动响应,尤其是动力总成悬置系统到车身的输出功率流,必须知道系统的激励力信息[9]。
车架的刚度远大于橡胶悬置刚度,故在辨识激励力的过程中将车身与车架视为刚体。动力总成悬置系统包含6个自由度,汽车无论是在怠速工况还是行驶状态下,悬置的车身连接点都有振动,为了消除车身振动对激励力辨识实验结果的影响,悬置点振动数据采用的是它相对于车身悬置点的振动响应。实验需要测量3个悬置各自发动机一侧和车身一侧的振动响应,两者相减即为悬置点振动加速度。
本实验共6个测点,采用6个三向加速度传感器,用磁座固定法安装加速度传感器,磁座法安装简单易拆卸,且满足本次测量频率范围要求(1~200 Hz)。部分实验测点布置如图2所示。

图2 后悬置加速度测点Fig.2 Measure points of rear mount
实验同时测量18个通道的加速度信号,通过BBM数据采集仪采集数据,设置采样频率4 096 Hz,总采样时间30 s,实验结束后可从中选出部分较稳定的信号。
发动汽车后,待发动机转速稳定后,首先测试怠速工况各个测点的振动信号,记录3次数据。然后开动汽车,进行匀速工况的测试,同样记录3次数据。为了减少路面激励对测试的干扰,尽量选择较平直路段进行测试。实验结束后可以通过下式反求动力总成激励力
(5)
式中:{F0}为动力总成质心等效激励力;[M0],[K0]为动力总成六自由度系统质量矩阵和刚度矩阵;[Sa]为[S1],[S2]和[S3]组成的9行6列矩阵,表示动力总成6个自由度方向上的位移引起悬置点移动的位移转移矩阵;{A}为3个悬置点振动加速度矩阵。
2.2 悬置点导纳测试实验
悬置点导纳矩阵[H]为拆除动力总成之后悬置点之间的加速度导纳函数矩阵。动力总成通过悬置固定在横向副车架上,悬置与横向副车架为螺栓连接。实验采用的方案是拆除动力总成与副车架之间的连接螺栓,用千斤顶将动力总成支撑起来,使动力总成与副车架和车身分离,如图3所示。用手可以轻易晃动橡胶悬置证明动力总成与车身已经分离,再测试悬置点之间的导纳函数。

图3 与副车架分离后的悬置系统Fig.3 Mount system separated with subframe
为了在各个测点处方便布置加速度传感器与激振器,在各个悬置点位置安装一个小立方块,立方块为铝制,质量较小,可以尽可能减小对测量结果的影响。激振器采用型号为LMS-QSOURCES MINIATURE SHAKER,这是一种微型激振器,具有结构小和自支撑等特点,内部集成的传感器可以采集力信号和加速度信号,加速度传感器采用小型三向加速度传感器,用502胶水将加速度传感器和激振器安装在立方块面上,如图4所示。每个悬置位置都要布置三向加速度传感器,每组测试完成后将激振器改变安装方向或对应悬置位置,共需要9组实验完成整个悬置点导纳函数的测试。

图4 激振器与加速度传感器布置Fig.4 Sensor and vibration exciter arrangement
通过LMS软件设置激振器激励信号为0~256 Hz的扫频信号,每秒内扫频十次,每次测试时间为10 s。
实验结束后,根据激励信号与响应信号的相干系数判断有效频率范围,在50 Hz以上,原点导纳和跨点导纳相干系数接近于1,而50 Hz以下相干系数较差,这是由于激振器的有效频率范围在50 Hz以上,50 Hz以下的振动能量没有被激发出来。
3 悬置点动力学特性灵敏度分析
在求解动力总成悬置系统振动方程以及计算传递功率流的过程中发现,除了系统的质量、转动惯量以及悬置刚度等参数外,弹性车身悬置点之间的导纳函数同样也是关键参数。它的大小既可以通过实验测得,也可以通过在车身车架有限元模型中提取导纳函数的方法得到。但是,由于在车身车架有限元模型建立过程中阻尼很难准确地选取,有限元模型往往与真实模型存在一定差异,为了获得更真实的结果,采用了激振器激励测量悬置点导纳函数的方法。
悬置点导纳函数是9×9×151三维矩阵,对应频率范围50~200 Hz共9个点的原点及跨点导纳。为了寻找对输出功率流影响最敏感的导纳对应悬置位置和方向,对悬置点动力学特性进行灵敏度分析,分析结果如表1所示。

表1 悬置点导纳对输出功率流灵敏度分析Tab.1 Mounting points admittance sensitivity to transmitted power
由表1数据可知,右悬置Z方向对应导纳灵敏度最大,减小右悬置Z方向关于悬置点的原点导纳和跨点导纳可以降低传递到车身的振动功率流,反之则会增大传递的能量。
4 悬置安装点位置的优化选择
4.1 确定悬置点最优位置
根据整车车身三维模型,利用Hypermesh软件对车身进行网格划分,单元质量检查以及赋予材料属性等操作,建立车身有限元模型,如图5所示。为计算悬置点间导纳做准备。Nastran作为世界最流行的大型通用结构有限元分析软件之一,可以在工业生产各个领域进行多种分析[10]。我们利用Nastran软件对车身悬置点之间的导纳函数进行计算,将计算结果在HyperView软件中进行后处理,得到悬置点之间的导纳函数。

图5 白车身有限元模型Fig.5 Finite element model of the body in white
车身悬置点附近有限元模型如图6所示。图6中黑点为左、右、后悬置在车身的安装点,其中右悬置1为原始安装点,2和3位置为假设的新安装点。根据灵敏度分析结果,输出功率流对右悬置Z方向的导纳最灵敏,改变右悬置安装点位置最能影响右悬置Z方向导纳,进而影响传递到车身的功率流。因此,在有限元模型中右悬置位置另取两点2和3,分别计算右悬置在原始位置1和改变后位置2和3处时,3个悬置点9个方向之间的导纳函数。在有限元模型中计算导纳函数时,选择施加单位激励力方向为右悬置Z方向,将模型提交到NASTRAN中进行计算,即可得到右悬置Z方向到各个悬置点之间的导纳函数。

图6 悬置点附近有限元模型Fig.6 Finite element model beside mounting points
比较右悬置在3个位置处Z方向导纳函数大小,判断安装点在哪个位置时,右悬置Z方向到各个悬置点导纳函数最小。实际计算结果下,有的频率变大,有的变小,为了评价不同悬置安装点对导纳函数大小影响,可以计算右悬置Z方向到9个位置导纳函数的2-范数,即所有关注频率下导纳函数的平方和再开平方,作为导纳函数大小的指标,结果如表2所示。
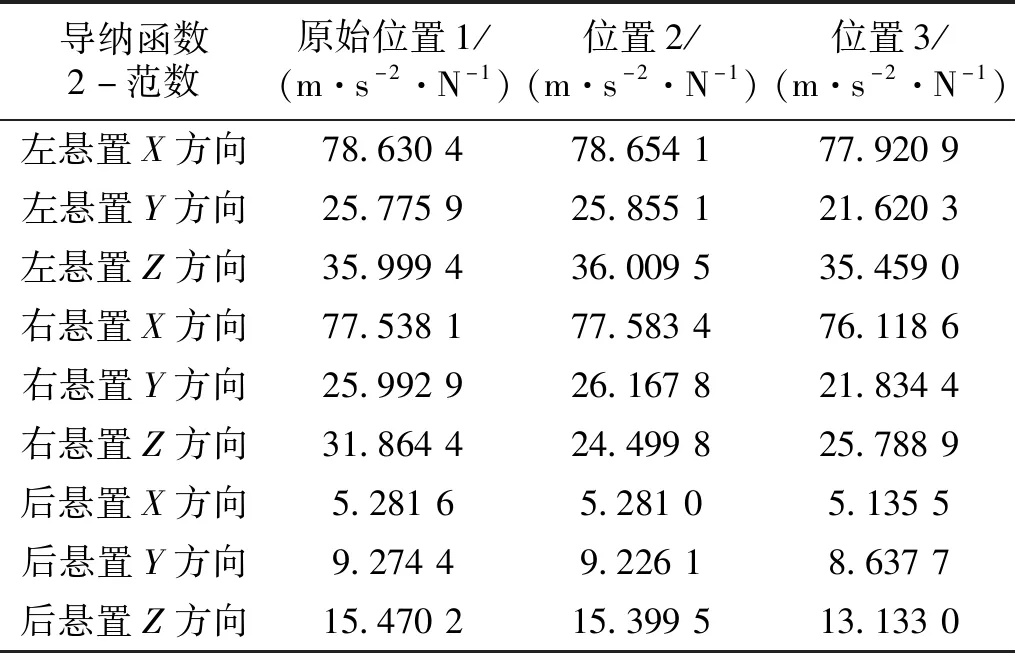
表2 不同悬置安装点位置导纳函数2-范数Tab.2 2-norm of mobility function at different mounting points
由于导纳函数的计算结果受有限元模型阻尼等参数的影响,导纳函数幅值会与真实值存在误差,甚至会存在奇异点,这也是表中跨点导纳要大于原点导纳的原因,但是仍然可以通过比较悬置点处于不同位置时同一组导纳函数2-范数的大小,来确定不同悬置点安装位置导纳函数的大小,进而判断对输出功率流的影响。
分析表2所示结果,悬置点安装位置在原始位置1和新位置2时,导纳函数2-范数变化不大,右悬置安装点位置位于3时,9个导纳函数2-范数相对于原始位置全部减小,将安装点位置向3移动可以降低对输出功率敏感方向导纳函数,而向方向2移动则没有明显效果。将右悬置安装点沿整车坐标系Y轴正方向移动为最佳优化结果。
4.2 悬置点位置变化对传递功率流和固有频率的影响
改变了悬置安装位置也会影响系统其它参数,从而影响传递功率流的大小,为了验证优化后悬置安装点位置传递功率流大小,按表3所列,将右悬置安装点沿整车坐标系Y轴正方向分别移动10 mm,20 mm,30 mm,40 mm和50 mm,并和原始位置下总传递功率流及动力总成悬置系统固有频率大小的进行对比。结果表明,沿Y轴方向移动距离越大,传递功率流下降越多,每移动10 mm降低0.25~0.3 dB,将右悬置安装点位置向右移动可以降低动力总成传递到车身的功率流大小。
对于沿Y轴方向移动右悬置安装点,系统固有频率的变化情况,动力总成悬置系统第一阶固有频率略有下降,但路面激励一般在2.5 Hz以下,一阶固有频率仍然远离路面激励频率。同时,各阶固有频率并没有因为悬置安装点位置的改变而变得过于接近,第三、第四阶固有频率相隔反而变大,这样有利于避免被同一个频率激发两个模态的共振。

表3 右悬置位置改变对输出功率流和固有频率的影响Tab.3 The influence of mounting points position to transfer power and natural frequency
4.3 悬置点位置变化对车身悬置点支反力的影响
为了比较悬置位置改变前后车身悬置点支反力的变化情况,计算了右悬置在不同安装位置时的支反力大小。左悬置车身位置和后悬置车身位置支反力都有减小,而右悬置车身位置支反力略有增加,但是由于车身悬置点的振速减小较大,所以总的传递功率流为减小的趋势,如表4所示。

表4 右悬置位置改变对车身悬置点支反力的影响Tab.4 The influence of mounting points position to reacting force on the body side
4.4 悬置点位置变化对TRA解耦率的影响
汽车发动机始终存在由爆发力引起的曲轴扭振,动力总成在收到这一扭振激励时,绕其旋转的轴称为扭矩轴(TRA轴),TRA能量解耦指系统在绕扭矩轴转动方向上解耦率达到100%,表5~表7分别为右悬置在原始位置、向Y轴正方向移动20 mm和40 mm后固有频率及TRA解耦率的大小,发现右悬置向Y轴正方向移动后,系统TRA解耦率明显提高。
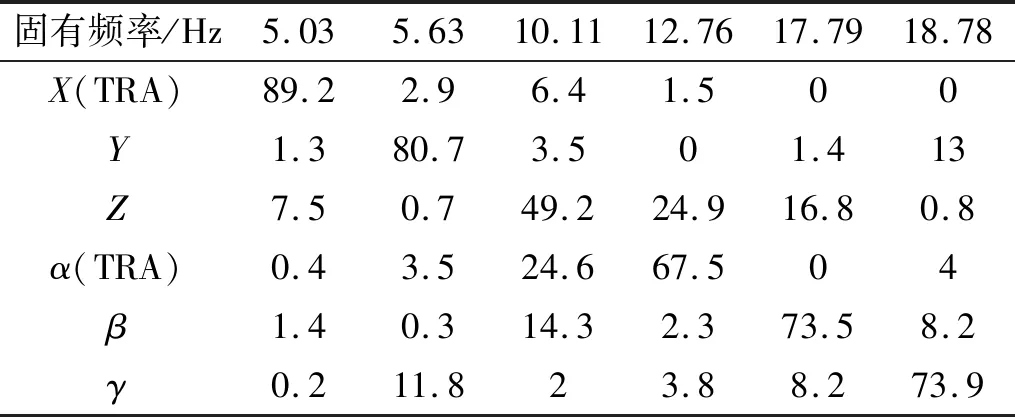
表5 原始状况固有频率及TRA解耦率Tab.5 The frequency and TRA decoupling rate of original system %

表6 右悬置移动20 mm固有频率及TRA解耦率Tab.6 The frequency and TRA decoupling rate of system after right mounting point moving 20 mm %

表7 右悬置移动40 mm固有频率及TRA解耦率Tab.7 The frequency and TRA decoupling rate of system after right mounting point moving 40 mm %
5 结 论
本文通过对悬置点导纳对于输出功率流的灵敏度分析,得到了最能影响动力总成悬置系统传递到车身功率流的悬置点位置和方向为右悬置Z方向,围绕与右悬置Z方向相关的导纳函数进行分析,在车身有限元模型中进行计算,向整车坐标系Y轴正方向移动的右悬置安装点可以降低导纳函数,降低传递功率流,进而降低整车的振动噪声。
在保持悬置点导纳函数不变的情况下,将右悬置位置向Z方向正向移动,动力总成传递到车身的传递功率流降低、系统TRA解耦率提高。悬置安装点位置改变后系统的固有频率分布没有恶化,除车身右悬置支反力略微增大外,其他悬置点支反力都有下降。
应当注意的是,由于会增大右悬置车身位置的支反力,在重新选定悬置安装位置的同时还应该增大右悬置安装点位置的车身刚度。
