线性动力分析的一种通用积分格式

王海波，何崇检,贾耀威

(中南大学 土木工程学院，长沙 410075)

结构的动力分析一直是工程研究的热门领域。传统的直接积分法，如中心差分法、Newmark法及wilson-θ法等在求解结构动力方程方面有着广泛的应用。但这些方法在建立积分格式时缺乏相应的变分原理的保证，因此存在能量耗散与相位误差，不能很好地满足工程实际的需要。

1994年前后，钟万勰[1]放弃了传统直接积分法中的差分格式，效仿哈密顿体系对偶变量的引入，提出了精细时程积分法，为结构的动力分析开辟了崭新的途径。对于线性齐次方程，精细积分法能利用其递推格式给出计算机意义上的精确解。而对于非齐次动力方程，钟万勰采用一次多项式来近似荷载项，其计算精度不是很高，且需要对状态矩阵求逆。Lin等[2]分别就荷载项为三角函数及傅里叶级数的情况给出了其解析解的表达式。文献[3-6]提出了增维精细积分法，该方法将非齐次项也看做动力方程的状态变量，将其纳入到求解中去，从而将非齐次动力方程转化为齐次动力方程求解。该类方法具有很高的计算精度，且不需要对状态矩阵求逆，但该类算法只适用于荷载项为几类特殊形式的情况。文献[7-9]提出了一类利用数值积分法，如辛普森求积公式等来求解非齐次项的动力响应的方法，但该类方法的计算精度略低，无法与通解的精度相匹配,而如若要提高计算精度，则需要增加积分点的个数，其计算量会随之急剧增加,因此，该类方法的计算精度与效率之间存在难以协调的矛盾。富明慧等[10]结合矩形积分公式与递推算法，提出了广义精细积分法。该方法不需要对状态矩阵求逆，且特解与通解具有相同的计算精度，具有十分优越的算法的特性。储德文等[11]讨论了精细积分法中积分方法选择的问题，指出了为保证精细算法的高精度，应根据荷载的性质选择适当的方法。

本文结合泰勒级数展开式和广义精细积分法，提出了一种避免状态矩阵求逆的线性动力分析的通用积分格式。该方法可用于任意激励下结构的动力响应的求解，具有广泛的适用性。数值算例证明了本文方法的有效性。

1 动力方程的广义精细积分法

线性定常系统的动力方程为

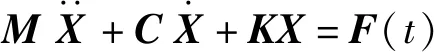
(1)

式中：M，C和K分别为质量阵、阻尼阵和刚度阵;X为位移向量;F为荷载向量。式(1)的初始条件为

(2)

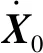
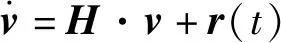
(3)

式中:v,H及r(t)有两种表达方式

(4)

或

(5)

式(4)为钟万勰效仿哈密顿体系引入偶变量的形式，式(5)为稍后发展出来的另一种形式。式(5)因为能同时反映系统的位移与速度，其应用更广泛一些。

利用指数矩阵，可将式(3)转化为同解积分方程

(6)

式中：Δt为时间步长。式(6)中的第一项为非齐次动力方程的通解，可用精细积分法精确得到。第二项为非齐次动力方程的特解，是本文讨论的重点。令

(7)

将时间步长离散为m=2N等份，N=20，令τ=Δt/m。由广义精细积分法可知，当r(t)为多项式时，可采用矩形积分公式与递推算法精确高效地求出式(7)。以三次多项式为例来说明这一过程，记

r(t)=r0+r1(ti+1-t)+
r2(ti+1-t)2+r3(ti+1-t)3

(8)

将式(8)代入式(7)，可得

(9)

其中,

(10)

式中：k=0,1,2,3,做变量替换s=ti+1-t，并注意到ti+1-ti=Δt，则式(10)可化为

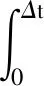
(11)

Sk与所在的区段无关，在整个计算过程中只需计算一次。记Y=eHτ，利用矩形积分公式对式(11)中各项进行数值积分，得

(12)

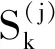
(13a)

(13b)

(13c)

(13d)

不难验证递推公式

(14)

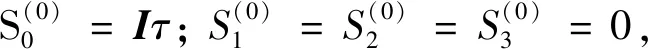
(15a)

(15b)

(15c)

(15d)

不难验证递推公式

(16)

式中：Ak为修正系数矩阵，其表达式为

(17)

Ak的选取项数与所需的计算精度有关，选取的项数越多，其修正的精度就越高。

2 特解的通用积分格式

广义精细积分法的核心思路在于矩形积分公式与递推算法，本文的笔者曾试图将其推广到其它荷载形式的情况，但均以失败告终。其根本原因在于，只有多项式与指数函数具有这种内在的递推性质。而将函数采用多项式来拟合，有两种方法，其一是采用拉格朗日插值多项式来近似，此即传统数值积分法采用的方式。另一种则是采用泰勒级数展开式来近似荷载函数，此即本文采用的思路。

在式(7)中，做变量替换，令t=ti+1-s，得

(18)

由泰勒中值定理可知，如果函数f(x)在含有x0的某个开区间(a,b)内具有直到n+1阶的导数，则对任一x∈(a,b)，有

(19)

式中：Rn(x)为拉格朗日型余项。根据式(19)可将r(ti+1-t)在t=0时刻展开成多项式

(20)

式中：t∈(0,Δt)令

(21)

式中：r为一个常向量；f(ti+1-t)为基本荷载函数，将式(21)代入式(20)可得

(22)

将式(22)代入式(18)中，可得

(23)

式中：Sk,k=0,1,2,…，n即为式(11)中的表达式。而rk,k=0,1,2,…,n的表达式为

r0=f(ti+1)

(24a)

r1=-f′(ti+1)

(24b)

(24c)

(24d)

此时，结合广义精细积分法即可精确地计算出非齐次项的动力响应。可以发现，式(24)中rk为变量，在计算过程中需要不断更新，但这只涉及到标量运算，不会显著增加运算量。下面就几种常用荷载形式给出其逐步积分公式。值得注意的是，对于荷载项为正、余弦函数的情况，富明慧等将其转化为复指数函数，也可利用广义精细积分法求解出结构的动力响应。考虑到复指数函数运算的复杂性与本文方法的完备性，下面仍给出荷载项为正、余弦函数时的逐步积分公式。

(1)非齐次项为sint的情况

(25a)

(2)非齐次项为cost的情况

(25b)

(3)非齐次项为et的情况

(25c)

(4)非齐次项为ln(1+t)的情况

(25d)

(5)非齐次项为(1+t)a的情况

(25e)

(6)非齐次项为tet的情况

(25f)

式(25)给出了高阶导数具有通式的荷载项的积分公式，对于其它一般的荷载项，只需求出其前几阶的导数形式代入式(22)即可求出其非齐次项的动力响应。因此，本文提出的算法具有广泛的适用性。

3 计算过程

综上所述，线性系统在任意激励下的动力响应求解可归纳为以下步骤：

步骤2 在各区间[ti,ti+1]上将非齐次项展开成式(22)的形式；

可以发现，步骤1在整个计算过程中只需要计算一次，这也是递推算法的高效性所在。此外，修正后的系数矩阵具有很高的精度，因此，本文算法的主要误差来源于非齐次项的拟合误差。理论上，通过选取幂级数的项数，可以达到任意精度。

4 算例分析

表1 精细数值积分结果与精确解比较Tab.1 Comparison between the result of precise numerical integration and exact solution

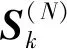
算例2考虑线性二自由度动力学方程

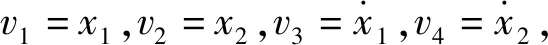
取初值v1(0)=2.5，v2(0)=v3(0)=v4(0)=1.0，本文算法在时间步长Δt=0.1 s,Δt=0.2 s,Δt-0.5 s时的前30 s分析结果见表2。

本算例采用五阶幂级数来拟合非齐次项。由表2可以看出，当Δt=0.1 s时，数值解基本可以保证七位有效数字；当Δt=0.2 s时，数值解基本可以保证五位有效数字；而当Δt=0.5 s时，数值解可以保证三位有效数字。这是由于数值解的精度主要取决于非齐次项的拟合精度，时间步长越小，其拟合的精度就越高，从而其数值解的精度也就越高。值得注意的是，由于本文算法采用的是利用积分区间端部时刻的幂级数来拟合非齐次项，因此选取的时间步长不宜过大。

表2 v1的数值结果比较Tab.2 Comparisons of numerical result of v1

算例3考虑动力方程

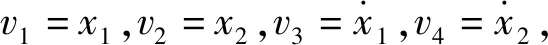
取初值v1(0)=2.5，v2(0)=0，v3(0)=v4(0)=1.0。该动力方程的解析解为

取时间步长Δt=0.5 s，各种方法的计算结果见表3。

本算例选用的时间步长较大，故此处选用六阶幂级数来拟合非齐次项。由表3可以看出，当时间步长较大时，HPD-L的线性化假设不能很好地拟合非齐次项，会带来很大计算的误差。增维法此时能得到精确解，且由于其计算格式简单，所以虽然增加了矩阵的维数，其计算时间仍然很短。但值得注意的是，对于非齐次项为其他形式的情况，增维法需要将非齐次项三角函数化，这本身就会带来较大的误差，因此其适用范围有限。同时可以看出，尽管时间步长较大，科茨公式与高斯公式(三阶)仍能给出高精度的解，且其计算效率也很高，这说明传统的数值积分方法能有效地求解非齐次项的动力响应。本文算法由于采用了高阶次的幂级数来拟合非齐次项，故其精度很高，但同时，其计算效率也略低。其主要的原因在于计算系数矩阵需要花费较长的时间。但同时也应注意到，系数矩阵只需要计算一次，当时间步数较大时，其简单的计算格式能弥补这一缺陷。本文算法最大的优势在于其简单的计算格式，不必求解积分系数，只需要执行一系列循环语句即可求解出非齐次项的动力响应，同时，通过选取幂级数的项数，可以达到任意精度。

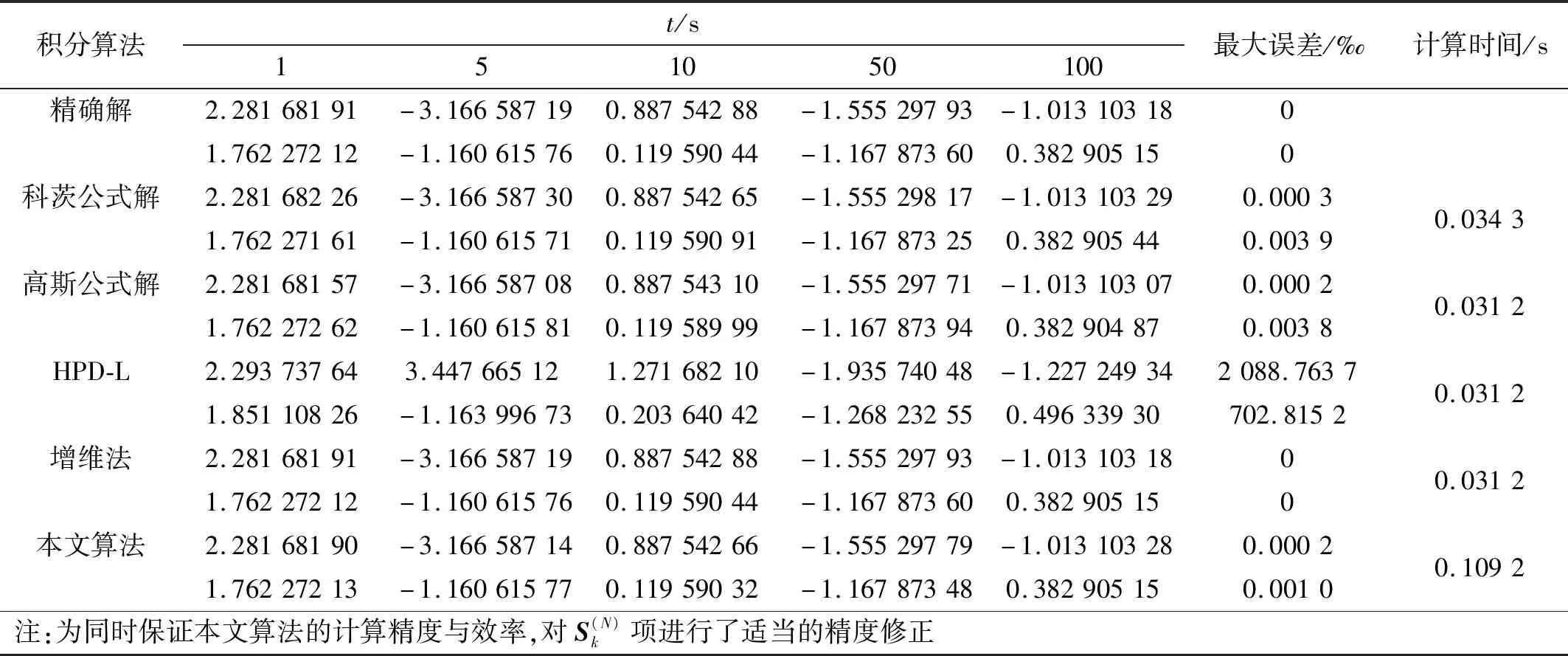
表3 v1,v2的数值结果比较Tab.3 Comparisons of numerical results of v1 and v2

5 结 论

(2)本文的实质是对广义精细积分法的扩展，通过采用幂级数来拟合非齐次项将其推广到任意荷载形式的情况。同时，本文算法也可以看作传统数值积分法的补充，两者的实质都是采用多项式来拟合非齐次项，而本文算法的优势在于其简单的计算格式，不需要求解积分系数，只需要执行一系列循环语句即可求解出非齐次项的动力响应，适宜于编程。