樟子松人工林生长与收获预估模型的研究

许家春

(黑龙江省第一森林调查规划设计院，黑龙江牡丹江157009)

林分生长模型概念的提出始于1887年，人们尝试用数学函数式去估算林分的生长发育过程，研究建立了众多的林木生长模型。但早期林木生长模型均针对特定的林分密度来预估林分的生长与收获，在林分经营实践中应用范围较窄。到20世纪60年代，随着多元分析理论的完善和计算机技术的发展，林分生长模型首次引入密度因子，实现了预估模型密度可变性。可变密度全林分模型的出现将通过数学模型模拟林分的自然生长过程，合理预估未来林分生长和收获量变为了可能，生长预估模型得以广泛应用于森林经营实践中。

在柴河林业局樟子松人工林二类森林调查数据的基础上，建立了23个标准地，以可变密度全林分预估模型理论为指导，通过数据拟合建立了樟子松地位级指数及林分密度指数经验方程，并在此基础上得出了樟子松人工林断面积生长预估模型和林分蓄积量预估模型。本文建立的预估模型充分考虑了立地质量、林分密度对林分生长的影响，以及自然枯损对蓄积量的影响，能够很好的模拟自然条件下林分的生长状况，具有密度可变、精准度高的特点，对本地区樟子松人工林的合理经营措施的制定具有一定的指导意义。

1 数据来源与分析方法

1.1 基础数据

2010年秋柴河林业局樟子松人工林二类森林调查建立标准地23个，标准地林龄18～42年，经营密度1475～4138株/hm2，常规经营，林相整齐，保持完整。标准地面积0.1 hm2，每木检尺，调查指标林龄、密度、胸径和树高，计算林分平均直径、平均树高及每公顷断面积。每块标准地选择1株标准木按1m分段锯取解析圆盘，按平均断面积求积法计算单株材积，拟合胸径、树高与单株材积的求解公式，计算每公顷蓄积及枯立木蓄积。建立数据库，使用SPSS、SAS分析软件进行数据分析、曲线拟合。

1.2 地位级指数和林分密度指数方程的拟合

根据可变密度全林分预估模型理论的要求，试验首先要建立地位级指数方程和林分密度指数经验方程，再结合林分密度动态预估建立断面积预估模型和蓄积量预估模型。

2 结果与分析

2.1 林地地位级指数方程的拟合

林分蓄积即林木单株材积的总会，而林木材积生长受立地条件的影响较大，要对不同林分蓄积生长量进行预估，就有必要对林分的立地条件进行分类。地位级指数是评价立地质量的重要指标，它以基准年龄时林分平均树高作为评价林分质量的数量指标，广泛应用于我国林木经营实践中。

本文以23块标准地平均树高、年龄数据为基础，利用SAS统计软件进行地位级指数导向曲线HT=Aexp(-k/t)的拟合与检验，结果见表1。

表1 樟子松人工林地位级指数导向曲线拟合结果

由表1可以看出：方程拟合的剩余标准差(Sy.x)为2.2063，相关指数(R2)0.6782，方程拟合结果满足统计分析精度要求。按照地位级指数计算公式SCI=HTexp[-k(1/t0-1/t)]，以40年为基准年龄(t0)，计算结果表明，23块标准地中地位级指数22的6块、地位级指数20的5块、地位级指数18的8块、地位级指数16的4块。

2.2 林分密度动态预估模型及密度指数方程的拟合

林分抚育间伐及自然枯损都会造成林分密度的减少，同时密度对林分生长的影响较大，要模拟自然条件下林分蓄积生长的变化规律，就必须研究林分密度的动态变化。相关研究表明，林分密度与地位级指数呈正比例线性相关。本文在前人研究的基础上选择未经抚育间伐的固定样地，查阅时间跨度12年的4次二类调查数据，通过其株数变化规律建立了樟子松林分密度动态预估模型：

N2=N1exp[-(0.011+0.0003SCI)(t2-t1)]

式中：N1、N2分别为时间t1、t2时林分每公顷株树；SCI林分地位级指数。

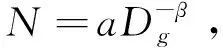
表2 樟子松人工林密度指数方程拟合结果

由表2可以看出：经验方程拟合的剩余标准差(Sy.x)为1.1384，相关指数(R2)0.8931，拟合效果较好。通过建立的林分密度动态预估模型可以预估未来某一时刻林分每公顷株树(N)，再根据密度指数公式SDI=N×(D0÷Dg)-B估算未来某时刻林分的密度指数，式中：N为每公顷株树；Dg为林分平均胸径；D0为基准直径15cm。

3 林分蓄积量预估模型的建立

在估算林木单株材积时，常常是通过由胸径、树高两项指标组合而成的经验方程来完成的，因此，胸径指标是估算材积值的重要指标。对林分而言，林分断面积与蓄积量关系极为密切，同时林分断面积受林分密度、立地质量影响较大，因此，要建立林分蓄积量预估模型，就有必要先建立林分断面积与林分密度、立地指数的经验方程。以23块标准地4次二类调查数据为基础数据，通过SAS数据分析软件，采用多元回归的方法建立了樟子松林分断面积、林分蓄积生长预估模型。

林分断面积BAS=7.648SCI0.4428exp(-6.7314(SDI/10000)-2.761t)

林分蓄积VOL=BAS×TH(34.1346/(TH+48.6497))

其中：SCI为地位级指数；SDI为林分密度指数；t为林分年龄；TH为林分平均高。模型拟合的相关系数在0.9以上，拟合效果较好。

4 林分蓄积估模型的应用与检验

以固定样地2010年(t1)调查数据为基础数据，通过模型预估2017年(t2)林分的平均树高、每公顷株树、林分密度指数、林分断面积以及蓄积量，同时与该固定样地2017年的实测值进行比较，以检验模型的预估效果，其结果见表3

表3 樟子松预估模型检验结果

由表3可以看出，通过模型公式估算的株树、树高、断面积及蓄积量与实测值差距不大，蓄积量误差为3.64%，精度96.37%。试验建立的樟子松生长与收获预估模型可以对特定林分未来某一时刻林分的生长性状及蓄积量进行预估，且模型具有较高的精确度。

5 结论

5.1 以可变密度全林分预估模型理论为指导，探讨建立了樟子松人工林地位级指数和林分密度指数经验方程，结合林分密度动态预估模型，建立了樟子松人工林断面积预估模型和蓄积量预估模型。BAS=7.648SCI0.4428exp(-6.7314(SDI/10000)-2.761t)VOL=BAS×TH(34.1346/(TH+48.6497))

5.2 以早期固定样地调查数据为基础，通过数学模型预估7年后林分生长性状及蓄积量，并与实测值进行比较检验，结果表明：建立的蓄积预估模型误差为3.64%，精度96.37%。建立的樟子松生长与收获预估模型可以对未来林分的生长性状及蓄积量进行预估。