教室座位问题的建模分析

2019-10-18李文秀

价值工程 2019年25期

李文秀

摘要：教室座位在很大程度上影响着学生的听课效率和学习状态，对于听课学生有着重要的现实意义。而同一教室内的不同座位的视觉效果有着较大的区别。本文旨在以高中生教室为研究对象，量化视角与仰角对学生视觉效果的影响，建立离散加权模型，通过满意度函数得到教室中不同座位的满意度。

Abstract： The classroom seating greatly affects the students' efficiency and learning status， which has important practical significance for the students. The visual effects of different seats in the same classroom are quite different. This thesis aims to study the influence of perspective and elevation angle on students' visual effects， establish a discrete weighted model， and obtain the satisfaction of different seats in the classroom through the satisfaction function.

关键词：数学建模;教室座位;满意度函数

Key words： mathematical modeling;classroom seating;satisfaction function

中图分类号：O242.1;F830.9 文献标识码：A 文章编号：1006-4311（2019）25-0231-03

1 问题重述

已知学生对教室座位的满意程度主要取决于视角？琢和仰角？茁。视角是学生眼睛到黑板上下边缘的视线的夹角，越大越好;仰角是学生眼睛到黑板上边缘视线与水平线的夹角，太大使人的头部过分上仰，会引起不适，一般要求仰角？茁不超过30°。

设教室的黑板高为h，黑板上边缘距离地面高为H，第一排和最后一排与黑板的水平距离分别为d、D，学生的座高为l（指眼睛到地面的距离）。已知参数h=1.50，H=2.60，d=1.96（单位m）。

求解以下问题：

①座高l=1.20m的学生的最佳座位在何处？

②假设学生的平均座高为l=1.20m，求每一排座位的满意度。

2 问题分析

学生对座位的满意程度主要取决于听课时的视角和仰角，而最佳位置就是要综合考虑这两个因素，使学生对座位的满意程度达到最大。本文通过对视角？琢和仰角？茁取权重，从而建立满意度函数。

问题一，以座高1.20m的学生为例，求出最佳座位所在，即需要求出满意度函数最大值，建立离散加权的函数模型并求解;

问题二，在对问题一中的满意度模型进行计算和分析后，对原有的满意度模型进行优化，再求出每一排座位对应的满意度。

为了更好地分析和求解问题，本文作出如下假设。

3 模型假设

①忽略因视力、光线等其他因素影响学生的满意度;

②学生对座位的仰角的满意程度呈线性;

③学生对座位的视角的满意程度呈线性;

④相邻两排座位间的间距相等，为x0=1.12m;

⑤所有学生的座位等高，为平均座高l=1.20m。

4 符号说明

符号说明见表1。

5 模型的建立与求解

5.1 问题一

针对问题一，考虑座高为1.20m的学生在教室里的最佳座位。视角越大越好，仰角不能超过30度。综合考慮视角与仰角的影响，分步建立满意度模型。

5.1.1 模型Ⅰ的建立：在仰角满足条件的情况下，学生满意度只取决于视角

如图1所示。

由图1可得

代入，解得最大视角为？琢=33.0549°，仰角为？茁=30°，x=0.50114m。考虑教室的实际情况，每排座位的间距为1.12m，所以现实中对应的最佳座位应该是第二排座位。此时，视角为？琢=26.3036°，仰角为？茁=24.444°，x=1.12m，与黑板的距离为3.08m。

5.1.3 模型Ⅱ的建立：离散加权模型

以模型Ⅰ所得结果为基础，在仰角不超过30°的范围内，量化计算仰角与视角对学生座位满意度的影响。每排座位前后间距为x0=1.12m。

对模型Ⅰ进行修正，将座位连续情况离散化可以得到：

学生对座位的满意度受到视角和仰角这两个因素的影响。对每一排座位的视角和仰角，运用极值化法进行无量纲化。对于第k排座位，建立学生对视角？琢、仰角？茁的满意度函数如下：

式中？琢k，？茁k为第k排座位上学生视角和仰角，？琢max，？茁max表示最优满意度，？琢min，？茁min表示最差满意度。

设视角？琢、仰角？茁在综合满意度Sk中的权重分别为c？琢，c？茁建立第排座位综合满意度函数如下：

根据模型Ⅰ，通过计算可以得出

主观给定权重C？琢=0.6，C？茁=0.4。根据模型，得到：

所以优化模型为：

5.1.4 模型Ⅱ的求解

为求解过程中表达简便，不妨设当x 单调递增时，（1.96+x）单调递增，S的分子部分单调递减，S的分母部分单调递增，所以S单调递减。因此当x取最小值时，S最大。

可得当x=kx0=1.12m时，最大满意度为S=0.529597，视角为？琢=26.3036°，仰角为？茁=24.4440°，最佳位置离黑板的水平距离为3.08m。

5.1.5 小结

在求解问题一过程中，我们通过两个阶段中逐步深入的探究，对仰角和视角数据无量纲化处理并主观给定了权重，建立了非线性离散加权模型。最后结论是座高为1.20m的学生的最佳座位应该是第二排座位。然而，我们在求解过程中发现了一些问题：人为给定权重缺乏一定的科学性;计算得到的满意度函数具有单调递减性，使得只要在满足仰角范围内座位越往前满意度越大;等等。因此，在问题二中，我们将对原有的离散加权模型进行修改，使得对教室座位满意度的分析计算更加科学严谨、符合实际。

5.2 问题二

一般情况下，公认的仰角范围是不超过30°。然而当下国内高中生每天处于高强度学习状态中，上课时间可以达到8至10节课。若长时间处在较大仰角的抬头状态，对于身体健康有着较大的危害。因此，我们在问题二中将仰角标准调整为20°，即仰角为20°时为最佳状态。另一方面，我们对视角和仰角数据进行一致化处理，即都转化为极大型数据，然后再通过变异系数法算出视角和仰角分别的权重系数，从而得到一个更完善的离散加权模型。

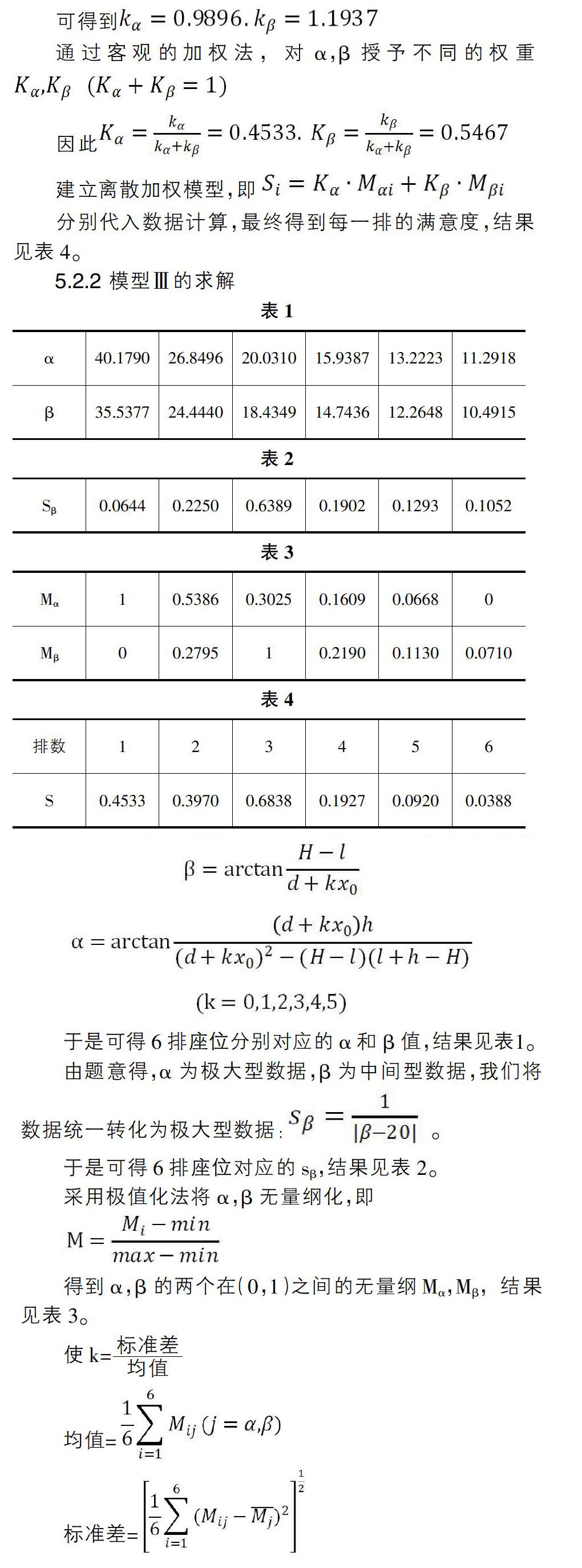
5.2.1 模型Ⅲ的建立：优化后的离散加权模型根据题意得于是可得6排座位分别对应的？琢和？茁值，结果见表1。

由题意得，？琢为极大型数据，？茁为中间型数据，我们将数据统一转化为极大型数据：。

由表4可得出结论，对于座高为1.20m的学生，最佳座位应该是第3排。

6 模型的评价与推广

6.1 模型的评价

优点：本文在问题一中建立了离散加权模型之后，又在问题二中运用极值化法、变异系数法对原有的离散加权模型进行了优化，得到了不同的各排座位满意度数据，从而使结论更加符合实际，使探究过程更具有说服力。

不足：本文在分析座位满意度时也忽略了一些其他因素，比如同一排座位不同位置的角度不同、前排学生可能挡住后排学生等等。这是本文的不足之处。

6.2 模型的推廣

本文的探究对于教室座位的设计有着重要的意义。设计教室时，应该充分考虑黑板高度、第一排到黑板距离、每排间距、凳子的高度等因素，从而使整体座位的满意度趋向于最大。同时，本文中的建立满意度模型的方法在设计影院、报告厅等过程中都能够提供很好的参考作用。

参考文献：

[1]熊斌，朱臻，苏勇编著.数学奥林匹克小丛书·高中卷2[M].二版.华东师范大学出版社，2012.

[2]沈文选，张垚，冷岗松编著.奥赛经典奥林匹克数学中的代数问题[M].三版.湖南师范大学出版社，2015.