各向异性模型图像增强算法的FPGA高速实现
2019-10-18张天祥刘瑞强刘艳莉张艳花张鹏程桂志国
张天祥,刘瑞强,周 冲,刘艳莉,张艳花,张鹏程,桂志国
(1.中北大学 生物医学成像与影像大数据山西省重点实验室,山西 太原 030051;2.哈尔滨工业大学 电子与信息工程学院,黑龙江 哈尔滨 150001;3.中北大学 信息与通信工程学院,山西 太原 030051)
随着传感器技术的发展,图像增强技术已经应用在工业检测、无人机识别、生物医学成像等多个领域.图像增强技术对于实时性要求越来越高,所以越来越多的应用领域要求降低算法的时延.实时性要求算法能够在1 s内处理25帧以上图像,才能满足人眼的视觉感受,使人眼不会感到卡顿的现象.图像增强算法中,偏微分方程的图像增强算法不仅能够提高图像对比度,也能较大程度地保留细节信息[1-2],但由于操作过程中图像迭代次数较多并且每次对整幅图像进行遍历,在CPU上执行图像的遍历计算的效率很低[3],运行Perona-Malik模型算法处理一帧图像的时间都在200 ms以上,很难实现算法的实时性处理.
现场可编程门阵列(FPGA)凭借其灵活性好、集成度高、并行处理、开发周期短等特点已经广泛应用于图像处理的各类加速应用中.近年来,将FPGA与传统嵌入式芯片的融合也成为了一种替代原有技术的方案.同时,将FPGA作为CPU外带加速卡已经被广泛应用[4],FPGA加速卡不仅能够为CPU快速实现算法,更有千兆网接口、PCIe接口等来保证超快速地传输数据.
因此,本文提出一种基于各向异性分散模型图像增强算法的FPGA硬件实现结构.该算法是在Perona-Malik模型基础上的一种改进算法,图像经过该算法处理后,对比度有所提高,图像细节明显增强.本文所设计的硬件结构通过参数表,流水线处理以及行缓存等操作实现.通过软件实现和Modelsim仿真对结果进行对比,根据主客观评价分析表明,将此算法实现在FPGA上,处理效果与软件实现近似,并且满足实时性处理要求.
1 图像的各向异性扩散模型
1.1 Perona-Malik模型
Perona-Malik模型是一种各向异性扩散模型,迭代格式十分简明,算法复杂度较低.模型如下:设图像定义在整个二维平面内,原始图像I(x,y,0)=I(x,y)随时间t演化为图像I(x,y,t)[5-7],演化规则为
(1)
式中:c(x,y,t)称作扩散函数,根据扩散函数的值是否趋近于0来判断图像在区域内是否需要平滑操作.
将I(x,y,t)定义为灰度图像的次迭代结果,(x,y,0)为初始图像.迭代形式为
I(x,y,t+1)=I(x,y,t)+
(2)
设可能的扩散函数c(x,y,t)
(3)
式中:常数K为扩散常数或者流常数,作为边缘强度的阈值.一般定义流函数为
Φ(x,y,t)=g(|I|)·I(x,y,t).
(4)
图1 中(a),(b)分别表示扩散函数和流函数.
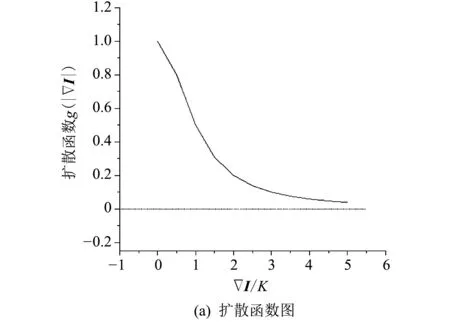

图1 Perona-Malik模型的函数图
图1(b)中显示随着流常数K的增大,平滑效果越明显,当I=K时,平滑效果最好,当I>4K后,平滑效果趋近于零.因此在图像边缘增强过程中,选择K使其略小于边缘的梯度幅度,有利于边缘增强[8].随着迭代次数的增加,图像的细节逐渐被模糊,只能停止扩散来保留图像原有的细节信息[9],限制了该模型在图像增强领域的应用.
1.2 改进型Perona-Malik模型
为了保留图像的细节信息,同时提升图像对比度,在Perona-Malik模型中融合锐化操作.改进后的模型不仅能够对背景区域进行平滑操作,也能够在边缘区域进行锐化操作,这样在提升对比度的同时也不会模糊掉图像的细节信息[10].类似传统的Perona-Malik模型,其迭代形式为
I(x,y,t+1)=I(x,y,t)+
(5)
式中:h(x,y,t)功能上是一个锐化函数,定义
h(i)=ω·[1-g(i)],
(6)
式中:g(i)为扩散函数;ω为锐化程度系数,0≤ω≤1.它决定了相应扩散系数的锐化程度.将扩散函数g(i)带入式(6)的c(x,y,t)中,得到
I(x,y,t+1)=I(x,y,t)+
(7)
式中:将g(I)-h(I)作为新的扩散函数,根据式(4)得出新的流函数
Φ(x,y,t)=
[g(|I|)-h(|I|)]·I(x,y,t).
(8)
图2(a)所示为不同ω值下的新扩散函数.在图2(b)中取定ω=0.2,当I>2.24K,即时,扩散函数和流函数降为负值,这里的正负值表明:对I>2.24K的边缘区域进行锐化操作,对I<2.24K的非边缘区域进行平滑操作.因此,选取合适的ω和K值,使改进型模型自适应地进行平滑或锐化操作,从而提升图像对比度并保留图像细节[11],本文选取=0.15和K=1来计算扩散系数.


图2 改进型Perona-Malik模型的函数图
2 基于FPGA的硬件实现
采用Xilinx公司出品的Zynq-7000 SoC开发平台,芯片型号为XC7Z020.开发平台有以下主要资源:ARM双核Cortex-A9处理器,处理器工作频率667 MHz,8个DMA通道,其中4个专用于可编程逻辑,PS端(ARM)与PL端(FPGA)通过AXI总线接口相连接,PL端含有85 000个逻辑单元(LE),53 200个查找表(LUT),106 400个触发器(FF),60个 36 Kb块RAM,220个可编程DSP切片[12],开发板工作电压为5 V.
2.1 算法硬件结构
通过Verilog HDL硬件描述语言设计改进型Perona-Malik模型,输入图像I(x,y,t)通过N次迭代处理后输出图像I(x,y,t+N),每次迭代处理都由4部分组成,并且使用流水线处理来达到提高运算速率的目的[13].硬件结构如图3所示.
首先将输入图像经过行缓存,当缓存的行数达到2行,即可与当前输入行的数据满足3行数据同时传输.当3行数据满足3×3的窗口处理模板后,通过窗口模板计算4个方向的梯度.然后将梯度值绝对值|I|传入参数表中进行查表操作得出每个方向的扩散系数,最后将输出图像和每个方向的值进行累加,得到一次迭代处理的结果.
在行缓存过程中,由于输入图像四周的像素不进行处理,为保证后续处理过程的统一性,如图4所示,通过计数器来判断像素位置,并添加1位标志位进入行缓存中,后续处理中只需判断标志位来决定是否需要对像素进行处理.

图3 Perona-Malik模型算法硬件结构图

图4 行缓存与流水线操作
流水线中参数表的建立是为了减少迭代过程中的复杂计算.首先将式(7)中的扩散函数g(I)-h(I)取定ω和K值,计算出扩散系数c.输入图像为8 b灰度图像,梯度绝对值|I|在[0,255]范围内.在迭代过程中,各个方向的计算结果是Si=|I|i×ci.所以参数表以梯度绝对值|I| 为索引,采用深度为256的ROM来存储各个方向的计算结果Si.
计算参数表时用定点小数表示浮点小数.用 8 bit 数据来表示小数部分,对于灰度值区间为[0,255]的8 bit灰度图来说,误差只要小于0.5,在灰度值取整过程中就不会出现图像信息缺失的问题.参数表实际值域为[-9.56,0.1],参数表使用8位定点小数表示后的最小分辨率为0.038,满足计算精度要求.所以,结合上文负数的补码表示,对参数表中数据保存格式如图5所示,有1 bit 符号位+8 bit整数位+8 bit小数位,等效于将数值扩大256倍,为保证小数部分截去的尾数误差更小,对结果加0.5后进行取整,则参数表存储的值域为[-2 448,26],均采用补码来表示.

图5 参数表数据保存格式
除行缓存外,该算法结构对每一帧图像一次迭代计算只需要经过3次加法计算和1次查表操作,避免了乘法以及平方等更加复杂的计算,计算过程经过4个时钟周期即可完成.
2.2 系统整体结构
系统采用Zynq平台实现,由Zynq芯片,OV5640摄像头、DDR3内存缓存、VGA/HDMI显示器构成.系统结构框架如图6所示,分为硬件设计(PL)和软件设计(PS)两部分,其中硬件部分包括数据采集模块、数据处理模块、数据缓存模块和图像显示模块.软件部分包括OV5640摄像头驱动、数据缓存和DMA驱动控制,软硬件之间通过AXI接口进行通信.

图6 系统硬件结构图
PS端最高工作频率设置为667 MHz,PL端从数据采集模块到DMA的工作频率为100 MHz,OV5640和图像显示模块工作频率为25 MHz.PS端初始化摄像头采集数据为YUV422格式,采集30 fps大小为640×480的图像,数据采集模块输出Y分量,即灰度图像.经过Video in AXI-Stream IP核后将有效数据传入数据处理模块[14,15].
数据经过处理后,通过PS端控制DMA传入DDR3内存中进行缓存,类似双缓冲机制,缓存3帧图像来保证系统能够同时接收和处理数据.输出显示时,VTC视频时间控制IP核给输出模块60 fps的VGA时序,所以在DMA与图像显示模块之间加入了FIFO作为数据缓冲,防止数据丢失.
3 结果及分析
3.1 软件实现及仿真结果对比
将该算法的软件实现与仿真的硬件加速结果做对比,选取ω=0.15和K=1.软件实现在2.5 GHz 的Intel Corei5-4200M CPU上通过VS 2013开发平台和OPENCV开发库完成.仿真处理在Vivado 2016.4,Modelsim和Matlab联合仿真下进行处理,为了与实际工程相符,设置工作频率为100 MHz.
选取两张256×256,一张400×292的灰度图进行对照实验,每张图像都经过8次迭代处理,结果如图7所示,其中第1列为选取的原图,第2列是使用C++语言通过VS 2013开发平台和OPENCV开发库的处理结果,第3列是使用Verilog HDL经过Vivado 2016.4综合后,再通过其附带的Modelsim仿真,产生数据文件后通过Matlab显示的处理结果.
通过观察图像、定量计算图像信息熵和对比度来评价参数选取后的处理结果.图像信息熵计算公式为
(9)
式中:i表示灰度图像灰度值,pi表示i在灰度分布中所占比例.图像信息熵越大表明图像中的细节程度越好[16].对比度计算公式为
C=∑δ(x,y)2·Pδ(x,y),
(10)
式中:δ(x,y)是相邻像素间的灰度差;Pδ(x,y)是灰度差为δ的像素分布概率.
图7 中处理结果的各项参数如表1所示.通过观察图7 和表1 中的结果可以看出,软件的处理结果与综合后的仿真结果在图像质量上相差无几.通过信息熵和对比度来看,其结果相差不大,参数提升范围也在同一数量级,说明通过Verilog HDL所实现的算法与C++所实现算法处理效果相同.但通过处理时间对比可知,经过硬件算法在FPGA上实现的处理速度将会是在计算机CPU上实现的300倍左右,加速效果明显.

图7 VS2013处理结果和Modelsim仿真处理结果

表1 处理结果的各项参数
3.2 硬件实现结果
将该算法在ZYNQ开发板上进行实现,将输出图像改为720 p图像,相应的输出时钟频率改为75 MHz,目的是将大小为640×480的原图与处理结果图拼接后进行对比,最终结果如图8所示.
图8 中左侧为处理后的显示图像,右侧为原图.图8(a)为遮挡物体采光后采集的低对比度图像,比较明显的是原图中因光照问题所模糊的投掷垃圾图案和花型图案,在处理图中可以清晰看到其轮廓细节.图8(b)为正常采集的图像,对比度相对较高,图像细节保留完好,根据处理后的结果来看,并没有出现过度锐化的现象,并且图像对比度也有一定提升,结果表明算法在该场景下适应性较好,所消耗各项资源如表2所示.

图8 实际场景处理结果图
4 结 论
本文在ZYNQ-7000平台上对一种改进型Perona-Malik模型算法进行算法加速.通过对照实验分析结果,该算法在PL端处理一帧256×256图像约为0.67 ms,满足算法处理实时性要求,使用Verilog HDL实现后处理效果与C++实现效果相似,并且在实际工程中处理效果较好,没有出现过度锐化和噪声等现象.
下一步的改进之处有:
1) 利用片内RAM,FIFO等其他内部资源解决触发器消耗较多的问题;
2) 先将数据存储,再通过DMA读出后进行处理[17],用于解决处理结果边缘有毛刺的问题.
