模糊聚类分析在异常振动振源识别技术中的应用研究

陈革维

模糊聚类分析在异常振动振源识别技术中的应用研究

陈革维

（深圳职业技术学院 机电工程学院，广东 深圳 518055）

聚类分析是工程应用中模式识别的重要工具．现代化高楼等工程系统具有多振源且振动特征复杂的特点，模糊聚类分析可以使分类的结果更切合实际．本文以时间序列分析理论为基础，通过对振动信号建立时间序列模型，采用主分量分析法对模型参数进行特征量提取，将模糊聚类分析方法应用于高楼异常振动的振源的实时识别，对机电设备等装置造成的异常振动可以实现有效识别．

模糊聚类分析；异常振动；识别

现代建筑结构日趋复杂，其附属的机电设备等装置也数量增多、功能多样化，往往造成建筑系统出现局部的异常振动，而不能及时有效地发现振源，影响建筑及其内部设备的安全正常工作．如何在建筑及其内部设备的正常运行状态下，实时识别异常振动的振源，从振动理论出发，解决该问题需要进行2个步骤：一是提取异常振动点及疑似振源的振动特征；二是对振动特征加以分析，识别其关联性．

时间序列分析理论和实际工程案例分析验证，采集振动信号，对所得到的振动时间序列信号建立时间序列模型，模型参数可以体现振动的特征[1,2]．通过建立二位坐标系来对比时序模型参数之间的相近关系，可以判定异常振动与振动源之间的关联程度，从而达到识别异常振动振源的目的[3]．为了使识别过程具有完整的数理统计分析理论支撑，进一步使识别过程达到由计算机进行的自动运算分析，以及使识别结果更加准确有效，减少人为因素影响所导致的误判，有必要将聚类分析方法引入异常振动振源的识别过程．聚类分析在工程应用中是模式识别的重要工具，由于实际工程应用中的模式识别大多具有模糊性，其分类问题多涉及到对象之间的关联程度，把模糊数学方法引入聚类分析，可以使分类的结果更切合实际．

大型建筑等复杂工程系统具有多振源且振动特征复杂的特点．利用传感器采集异常振动点及多个振动源在工作状态下发出的振动时序信号，通过建立时间序列模型提取振动的特征；基于模型参数，利用模糊等价关系对识别对象进行聚类分析，从而揭示异常振动与振动源之间的关联性，是实时发现异常振动的振源的有效途经．本文以工程实例对模糊聚类分析法在异常振动振源识别技术中的应用有效性进行研究分析．

1 振动信号采集

在实际工程案例中，某工科实验教学楼中部楼层的房间地板出现了无规律的异常振动，为分析其振动特征，利用压电式加速度传感器，以400 Hz的采样频率采集了该异常振动的加速度信号，如图1所示．

图1 异常振动加速度信号

基于应用领域，不同的时间序列模型及建模方法各有优势．在时间序列分析理论的工程应用中，AR模型的有效性在实际工程案例中得到了广泛验证[4,5]．该模型在对振动信号的分析中同样应用广泛，其模型参数可以较好的体现出机电设备及建筑物的振动特征．三阶自回归模型AR(3)的公式如下：

式中，自回归参数ψ属于无量纲数值；表示时序值；α属于白噪声[6]．

对上述所采集的异常振动加速度信号的10个时间序列建立10个AR(3)模型，得到10组自回归参数ψ、ψ、ψ见表1．

分析该实验教学楼的建筑结构及所安装的机电设备发现，安装在楼顶平台的抽风机驱动电机为疑似振源之一，该电机产生的振动可以通过建筑结构传递，在相应的固有频率等物理条件下，引起远距离的建筑构件出现异常振动．共采集10次该位置点的振动加速度信号，建立三阶自回归模型AR(3)，得到10组自回归参数ψ、ψ、ψ见表2．

大楼墙面的通风管道亦为疑似振源，管道内气体流动的无规律变化所引起其自身的振动，可以通过建筑结构传递，在相应的固有频率等物理条件下，引起远距离的建筑构件出现异常振动．共采集10次该位置点的振动加速度信号，建立三阶自回归模型AR(3)，得到10组自回归参数ψ、ψ、ψ见表3．

作为聚类分析的比较对象，选择楼顶平台地板共采集10次振动加速度信号，建立三阶自回归模型AR(3)，得到的10组自回归参数ψ、ψ、ψ见表4．

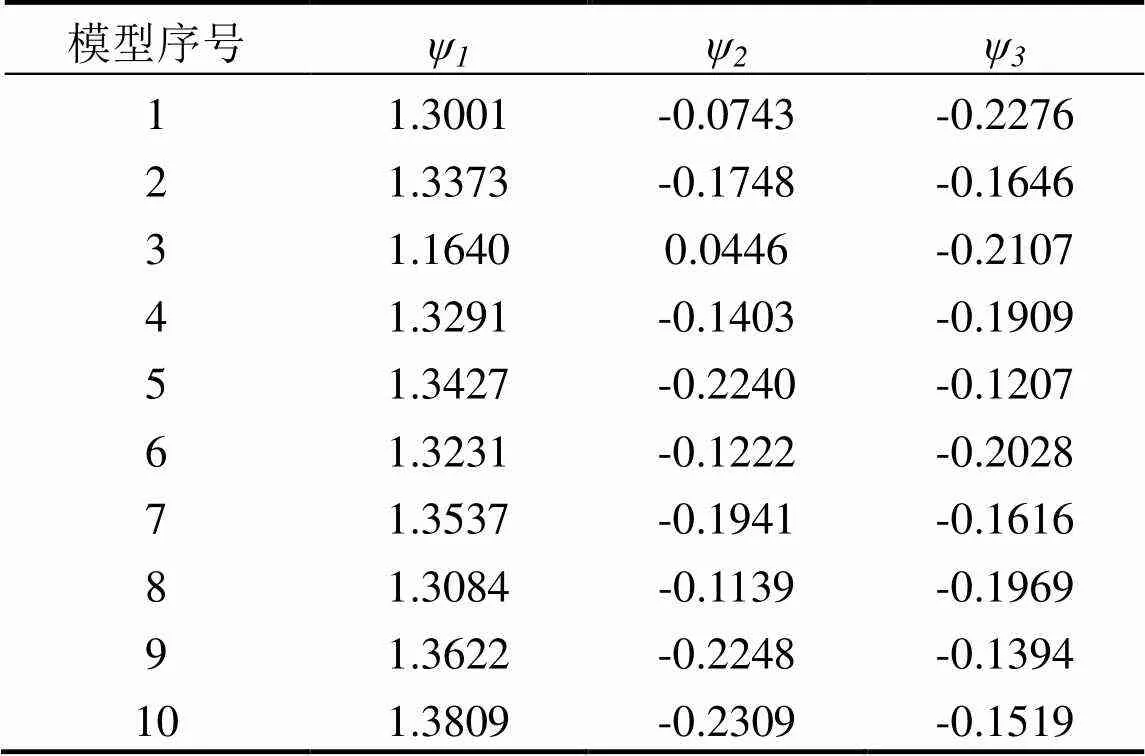
表1 异常振动时序模型参数

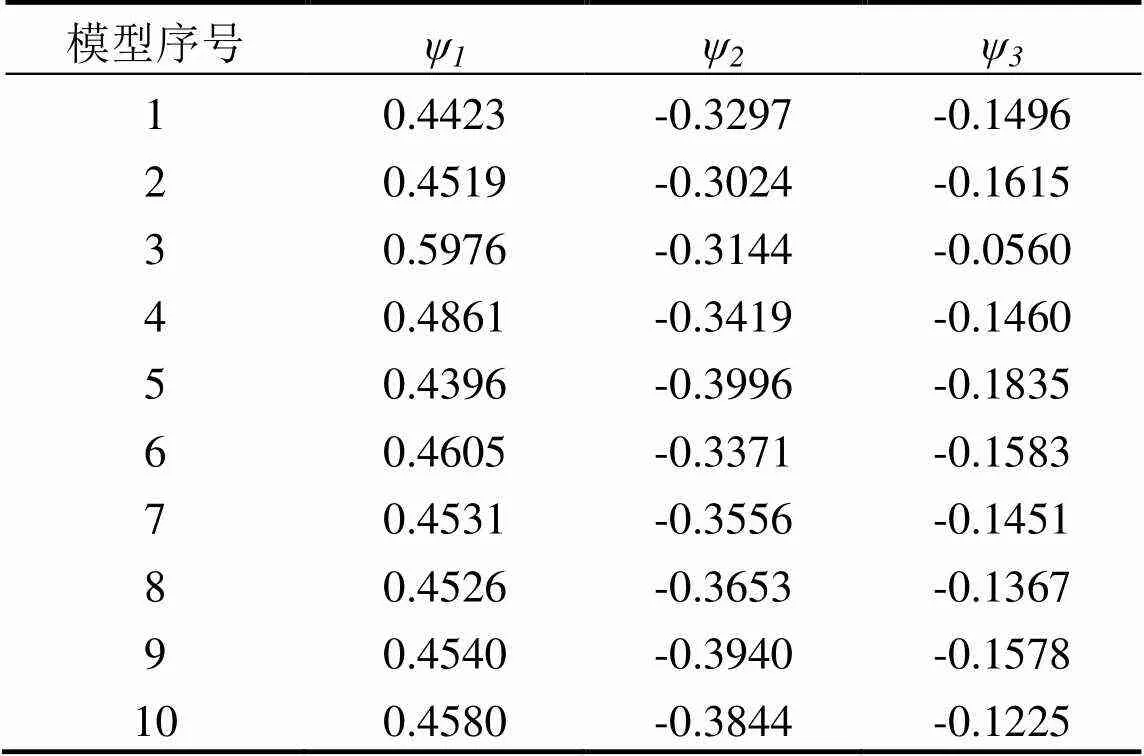
表2 电机振动时序模型参数

表3 管道振动时序模型参数

表4 平台振动时序模型参数

下面基于上述模型参数，通过模糊聚类分析法，利用模糊等价关系，分析不同位置点振动之间的关联性．

2 特征量提取

对模式识别而言，一个时序模型中不同阶的参数所起的作用并不相同，一部分参数具有明显识别效果，也有一部分参数可能无效．如果在识别过程中使用全部参数，由于各参数不一定相互独立，这不仅使识别中的计算量增大，无效的参数反倒会对识别效果产生不利影响，给有效识别带来困难．如何从多个模型参数中提取出有用的参数加以识别，这就是模式识别中的特征量提取问题．

特征量提取的实质，从数学意义的角度出发，是对已有的模式向量进行降维变换，所得到的低维模式向量应包含原有高维模式向量的代表性特征，即在粗特征中选出精特征，以减少识别工作量并保证识别效果．特征量提取的数学方法有多种，常用的有主分量分析法、Hadamard变换法，其数学路径都是基于对原有模式向量进行正交变换，使得到的新模式向量相互独立；再对新模式向量降维处理，提取出需要的特征量．2种方法各有优势，就识别效果而言，Hadamard变换法的识别精度略低于主分量分析法．

针对时序模型参数的特点，采用主分量分析法进行特征量提取，具体步骤如下[6]：

1）将维向量= [12…u]T的个训练样本按式（2）估计的自相关矩阵R，其中(j)是的第个训练样本.

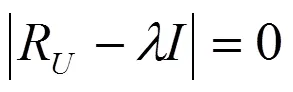
3）根据公式（3）计算结果，选择主分量对应之特征根λ，λ，…，λ．

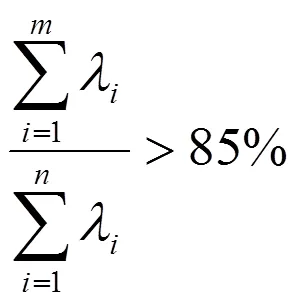
4）按公式算出(1)，(2)，…，(m)组成变换矩阵，其中α是中的第个行向量；

5）计算出特征向量，其中α为(i)中的第个元素：

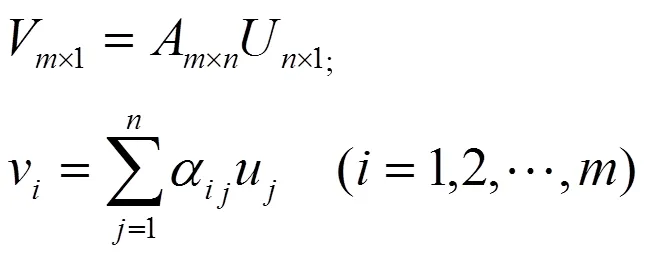
将上述时序模型AR(3)的模型参数组成3维向量，共40个训练样本，首先计算出其自相关矩阵R，再计算出特征根（表5）．

选择分量（1）、（2）为主分量，算出α并组成变换矩阵，最后算出二维特征向量

计算结果见表6．其中模型序号1~10为抽风机电机，11~20为通风管道，21~30为异常振动，31~40为楼顶平台．

表5 特征根值

3 模糊聚类分析

在模式样本划分之前，先要根据等价类分类目标定义样本相似性的测度，工程应用较多的测度包括以下4种：欧氏（Euclide）距离、马氏（Mahalanobis）距离、明氏（Minkowski）距离、角度相似性函数．

模糊聚类分析的基本步骤如下：

将需要对其进行分类的全体对象集合设定为：

其中的每一个对象对应于一组数据u，用以描述对象属性，u定义为

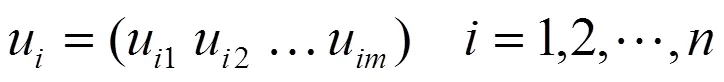
第一步为标定，即根据实际情况，按照某一准则或某种方法，给对象两两之间都赋以区间[0，1]内的一个数r，称为相似系数．r表示u与u之间的相似程度，它越接近于1，说明两者之间越接近．用相似系数来建立模糊相似矩阵：

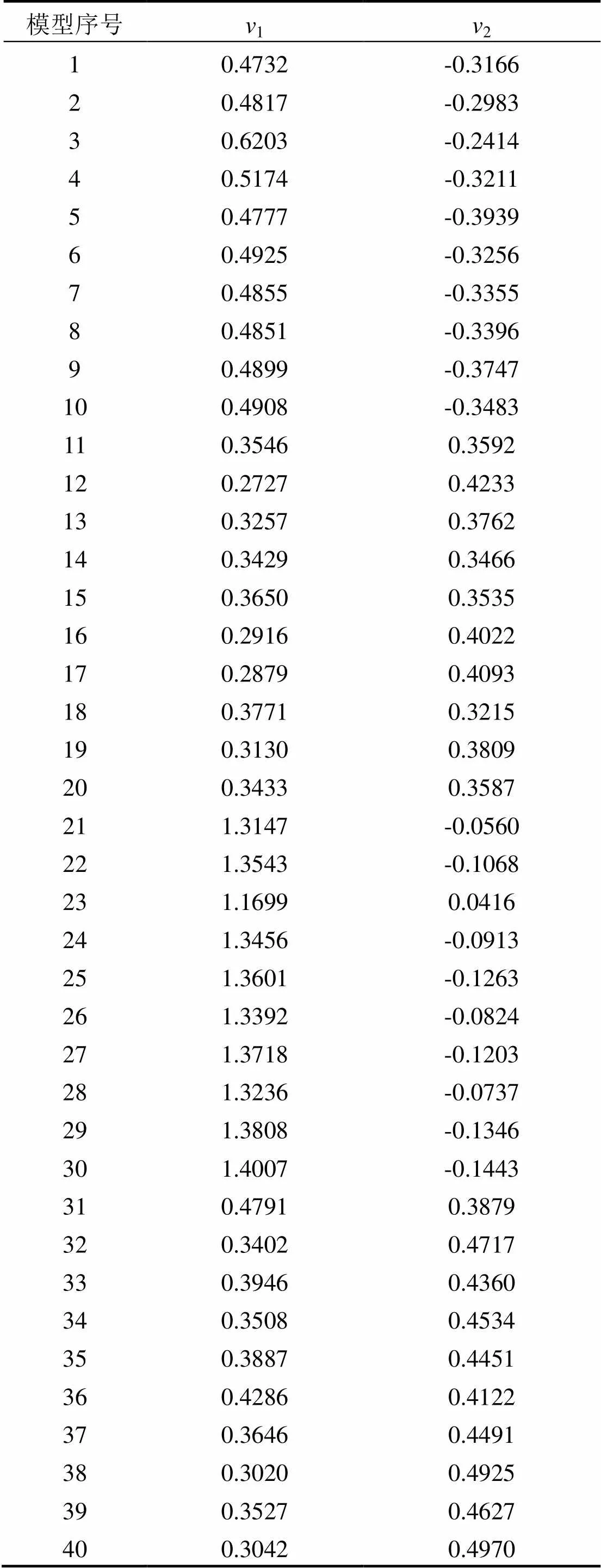
表6 特征向量值

第二步为聚类，采用逐次平方法，对所得到的模糊相似矩阵参数进行进一步计算，得到传递闭包，基于传递闭包所具有的模糊等价性，依次取－截阵，并按－截阵将分成相应的等价类．

模糊聚类的基础是相似系数，在计算相似系数的方法中，欧氏（Euclide）距离以及明可夫斯基贴近度法所采用的明氏（Minkowski）距离，都是基于对象样本参数所构成的“空间距离”．对于高维欧氏空间而言，由于对象样本分布的复杂性，难以实现有效的分类．因而从模糊聚类分析的数学基础而言，前述的特征量提取过程是必不可少的．

应用明可夫斯基贴近度法计算相似系数r．明可夫斯基贴近度法的计算公式为：

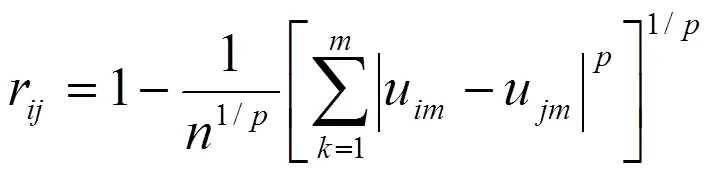
其中参数．

取=5，将前面计算得到的40组特征量代入公式计算相似系数r，建立模糊相似矩阵后，求出传递闭包．

取=0.95，等价类分类结果如下：

第一类：1，2，4~10；

第二类：11~20；

第三类：21，22，24~30；

第四类：31~40；

孤立对象：3，23；

可以发现，除2个孤立对象外，4个采样位置点的时序信号被相应的分为四类，说明四者的振动特征各不相同．

取=0.94，等价类分类结果如下：

第一类：1，2，4~10；

第二类：11~20，31~40；

第三类：21，22，24~30；

孤立对象：3，23；

可以发现，通风管道与楼顶平台的时序信号被归为一类，说明两者的振动特征相近．

取=0.51，等价类分类结果如下：

第一类：1~10，21~30；

第二类：11~20，31~40；

此时已无孤立对象，可以发现，抽风机电机与异常振动的时序信号被归为一类，说明与通风管道相比，抽风机电机与异常振动的振动特征相近．

取=0.5，等价类分类结果如下：

第一类：1~40；

此时4个采样位置点的时序信号已经全部被归为同一类．

4 分析与讨论

根据上述模糊聚类分析的等价类分类结果可以发现，4个采样位置点的时序信号可以被相应地分为4类，证明了分类的有效性．通过依次取－截阵，通风管道与楼顶平台的时序信号被归为一类，抽风机电机与异常振动的时序信号被归为一类，表明抽风机电机与异常振动的振动特征相近，抽风机电机是异常振动振源的可能性更大．这一结论在消除异常振动过程中得到证实，观察分析发现，由于抽风机电机由变频器自动控制，而变频器根据大楼中抽风柜开启数量而自动调节电机的电流频率．当电机电流频率为40 Hz时，异常振动出现．抽风柜开启数量的经常变化，导致异常振动不定时无规律地出现．改变变频器设置，使电流频率避开40Hz，异常振动消除．

通过不同的工程实例验证表明，建立时间序列模型可以提取振动的特征，但通过对时序模型参数建立二位坐标系来识别振动特征及关联程度的方法过于粗糙，且缺乏完整的数理统计分析理论支撑．而直接对时序模型参数应用模糊聚类分析，聚类效果亦不是很理想．应用主分量分析法对时序模型参数所构成的模式向量进行特征量提取，提取得到的特征量相互独立，去除了无效参数对有用参数的不利影响并实现了降维，在此基础上进行的模糊聚类分析，对振动特征具有较好的识别分类效果，证明模糊聚类分析法对异常振动振源的识别应用具有有效性．

[1] 张永强，荆建平，李亚伟，等．基于AR模型的转子典型故障诊断方法[J]．噪声与振动控制，2018（06）：155-160．

[2] 杨娜，代丹阳，秦术杰．古建筑木结构监测数据异常诊断[J]．振动工程学报，2019（01）：64-71．

[3] 陈革维，戴珏，王寒栋．高楼异常振动振源的实时识别技术研究[J]．噪声与振动控制，2009（04）：31-33，37．

[4] 黄红梅．应用时间序列分析[M]．北京：清华大学出版社，2016．

[5] 潘雄锋，彭晓雪．时间序列分析[M]．北京：清华大学出版社，2016．

[6] 杨叔子，吴雅．时间序列分析的工程应用[M]．武汉：华中理工大学出版社，1992．

Research on Application of Fuzzy Clustering Analysis in Distinguishing Technology of Abnormal Vibration Source

CHEN Gewei

（）

Clustering analysis is the important tool for pattern recognition in engineering application. Because the engineering system such as modern high building, has more vibration sources and complex vibration characters, the fuzzy clustering analysis can make the classification results more realistic. Based on time series analysis theory, this paper makes time series model of vibration signal and then picks characteristic quantity from the model parameters by principal component analysis. The fuzzy clustering analysis is used in the real-time distinguishing technology of abnormal vibration source in high building. It can distinguish the abnormal vibration made by equipment such as mechanical and electrical machines effectively.

fuzzy clustering analysis; abnormal vibration; distinguish

10.13899/j.cnki.szptxb.2019.05.002

2019-03-22

陈革维（1969-），男，四川绵阳人，副教授，博士，研究方向：振动检测与控制、机电一体化．

TU97；TB53

A

1672-0318（2019）05-0009-05