电网不平衡时三相VSR变流器解耦控制策略研究*

李正国孙晓莉孟凡琨

电网不平衡时三相VSR变流器解耦控制策略研究*

李正国1，孙晓莉1，孟凡琨1，2

（1.深圳职业技术学院 汽车与交通学院，广东 深圳 518055；2.华南理工大学，广东 广州 510800）

三相VSR变流器安全可靠运行要求其控制器可以快速准确地锁定正序基波电压分量的相位和频率，针对变流器在电压不平衡和畸变时产生非特征谐波，且三相电流不平衡，损耗增大等问题，本文提出一种基于解耦双同步参考坐标变换的控制策略，通过双dq变换和解耦计算检测出不平衡电网电压中正序分量和负序分量的参数，为变流器控制器消除电压不平衡影响提供信息和依据，在各种电压不平衡情况下进行了仿真实验，结果验证了该控制策略的正确性和有效性．

解耦控制；不平衡电压；同步参考坐标系

在电力电子变流装置运行中，各种不平衡是无法可避免的，在这种情况下，变流器（特别是一些大容量的整流装置[1]，如有源滤波器、静止无功补偿装置等）将产生一些非特征谐波，且三相电流不平衡、损耗大等，会使变流装置的性能下降，甚至烧坏整流装置[2]．为了保证变流装置在电网电压不平衡和畸变情况下安全可靠运行，必须快速准确地检测电网电压正序基波分量的相位和频率信息，为控制器消除不平衡影响提供必要的信息和依据，如文献[3-5]提出采用陷波器的方法来消除二次谐波分量的影响．

针对实际的变流装置，本研究通过分析基于单dq坐标变换的工作原理和存在的问题，提出采用双同步坐标变换的方法，通过双dq变换和解耦计算消除电压不平衡[6-8]的影响，同时在电网电压频率突变等情况下也能适用，并且仿真验证该方法的正确性．

1 双坐标系解耦分序法

式中，+1，-1分别正序电压和负序电压的幅值；

则有

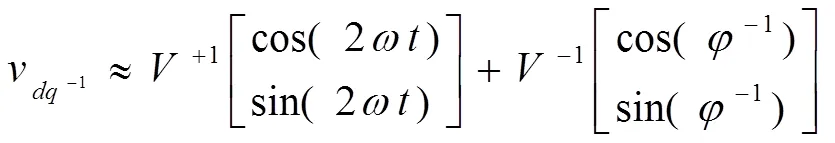
式（3）、（4）中，+1、-1坐标系下的直流分量与电网电压的正序、负序分量的幅值密切相关．

在三相不平衡状态下，一个电压矢量包括正、负序2个分量，分别以和的频率旋转，则电压空间矢量在两相静止坐标系下可表示为：

式中，φ，φ为正序电压矢量和负序电压矢量的初始相位角．

考虑2个旋转坐标系dq和dq，其相位角分别为和，其中为锁相环检测的相位角，如果锁相环能够完全锁相，即有，则电压空间矢量在dq、dq旋转坐标系下的分量为:

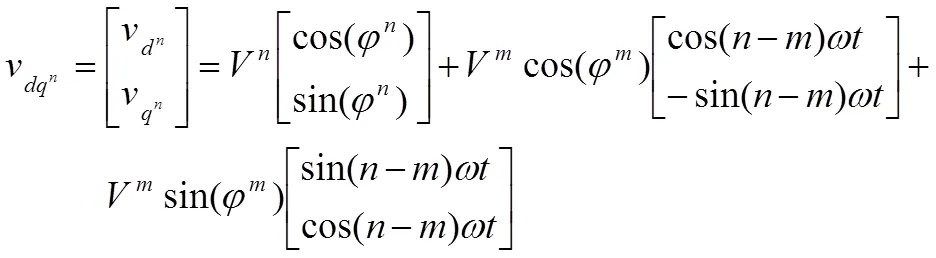
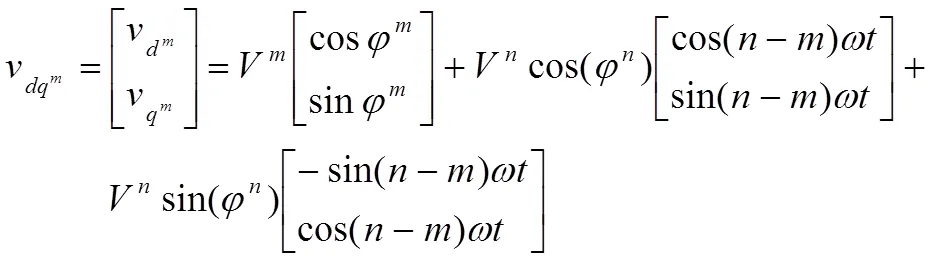
为了消除dq坐标系下信号的振荡部分，获取dq坐标系下信号的轴和轴分量，采取图1所示的解耦运算单元．

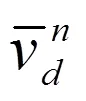
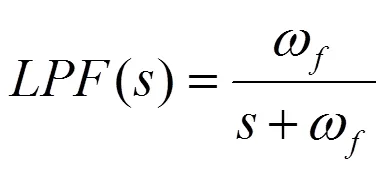
图2 dqn和dqm坐标系的解耦网络

对于图2所示的解耦网络，定义

解耦可得系统的状态空间方程为：

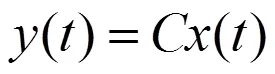
式中，

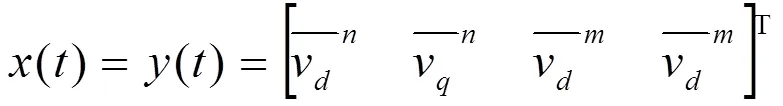
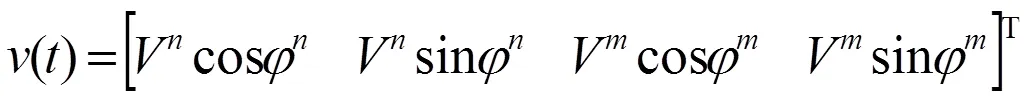
由状态空间方程可知，这是一个MIMO系统，为了简化分析，当=+1，=-1，则电压矢量分解到+1和-12个旋转坐标系上，系统原理框图如图3所示．电压空间矢量在+1、-1旋转坐标系下的分量为：

图3 解耦双同步参考坐标系

令

因此，双同步参考坐标系输出估计值为：

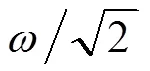
2 仿真结果与分析

1）当=0.1s时，A相发生单相接地故障，持续时间0.08s，仿真结果如图4所示．

2）当=0.1s，电网频率发生突变，由50Hz变为45Hz，持续时间为0.1s，仿真结果如图5所示．

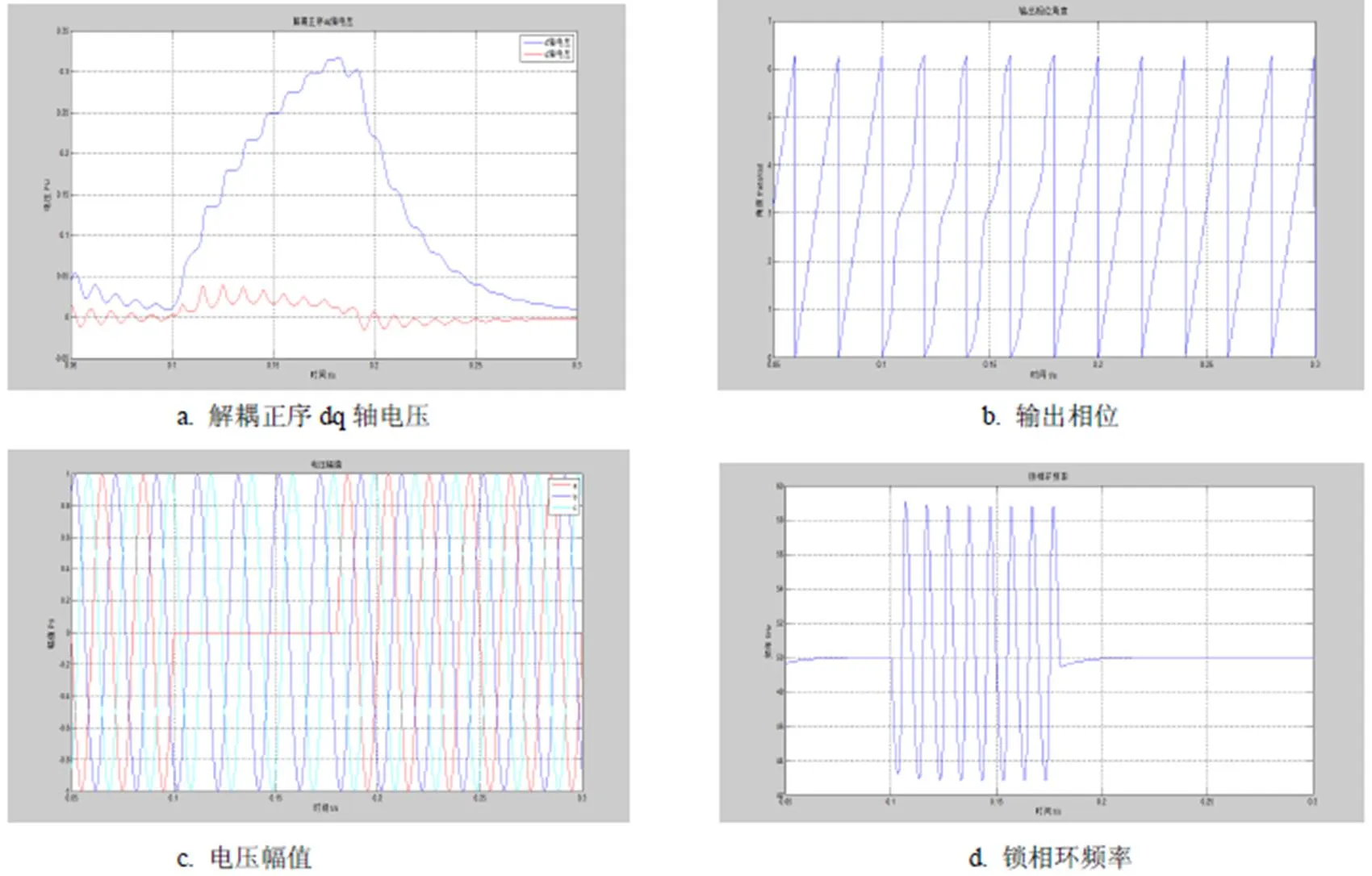
图4 单相接地故障时系统仿真结果图

图5 频率突变时系统仿真结果

3）当=0.1s时，A相产生正序3次谐波，幅值0.2（PU），初始相位角=25°，B相产生负序5次谐波，幅值0.1（PU），初始相位角=60°，持续时间0.2s．仿真结果如图6所示．

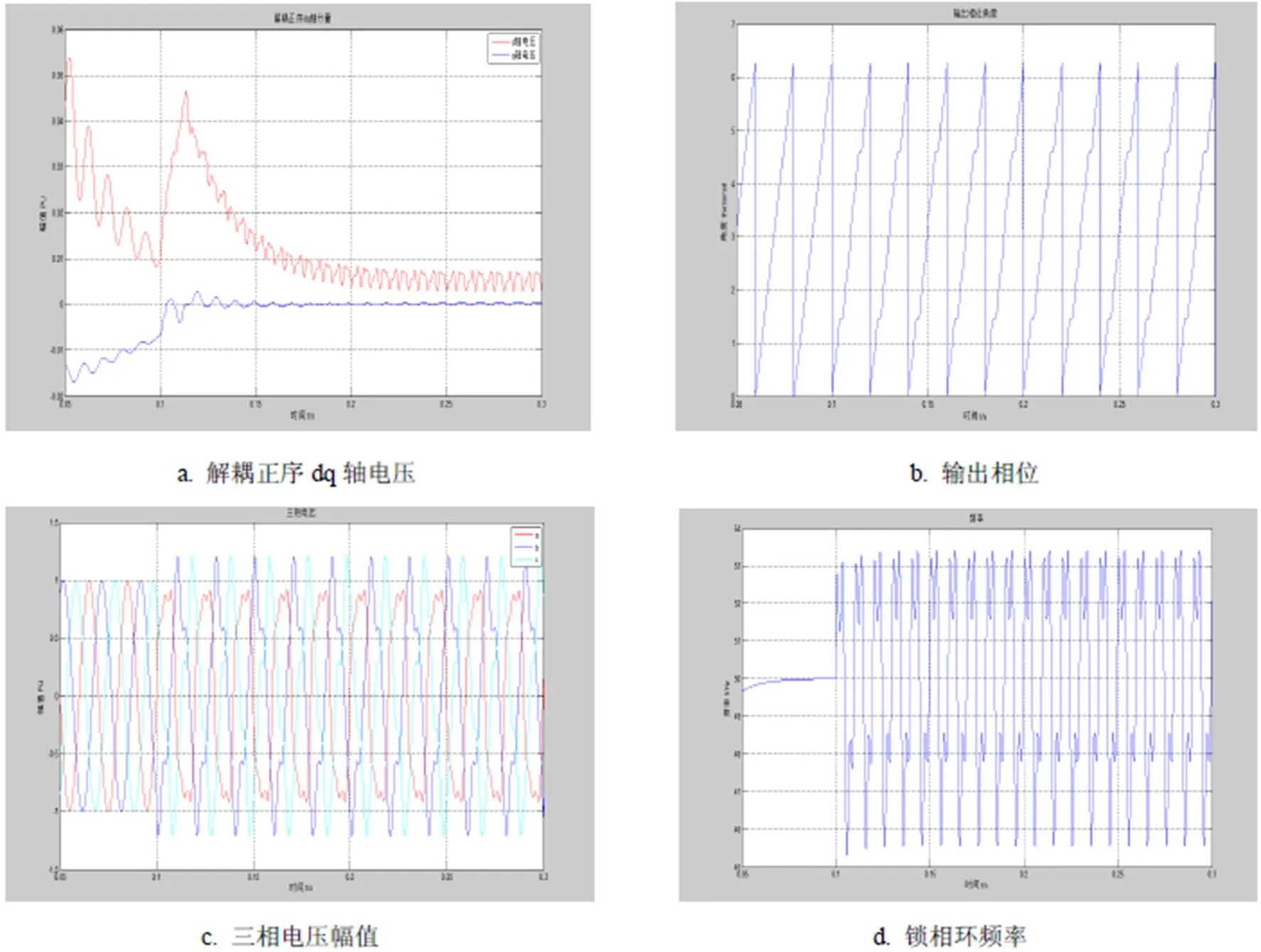
图6 含有谐波时系统仿真结果

从图4~6可得出：

1）当电网发生单相接地故障时，在稳态情况下，锁相环能够准确检测出正序电压相位以及电压频率，由于锁相环中有一阶滤波惯性环节，在一定程度上影响系统的动态响应．

2）当电网频率发生突变时，锁相环能够实现准确锁相，表现出了良好的频率自适应性．

3）当电网电压含有谐波时，DSRF解耦控制策略能够实现正负序解耦控制，消除非特征谐波的影响．

[1] Busquets-Monge S, Bordonau J, Boroyevich D, et al. The nearest three virtual space vector PWM- a modulation for the comprehensive neutral-point balancing in the three-level NPC inverter[J]., 2004，2（1）：11-15．

[2] Dugan R C, McGranaghan M F, Santoso S. Electrical Power System Quality[M]. 2ndedition. New York: McGraw-Hill, 2002．

[3] Okayama H, Uchida R，Koyama M, et al. Large capacity large high performance three-level GTO inverter systems for steel main rolling mill drives [C]/IEEE Pros IAS Ann Meet Conf Res, 1996：174-179．

[4] 张兴．电压型逆变器不同导电型电压矢量控制研究[J]．电气传动，1992（3）：2-7．

[5] 张纯江，张金泉，孙孝峰．空间矢量PWM波形的谐波仿真研究[J]．燕山大学学报，2000（2）：141-144．

[6] Bollen M H J. Understanding Power Quality Problems [M]. New York: IEEE Press, 2000．

[7] 许谨．自动连续多调谐滤波器的研究[D]．西安：西安理工大学，2006．

[8] Rodriguez P, Sainz L, Bergas J. Synchronous double reference frame PLL applied to a unified power quality conditioner[C]/ Proc IEEE Int Conf Harm and Power Quality, 2002，2：614-619．

[9] Pedro Rodriguze, Josep Pou Joan Bergas. Decoupled Double Synchronous Reference Frame PLL for Power Converters Control[J]., 2000，22（2）：584-592．

Three-phase Voltage Source Rectifier(VSR) Decoupling Control Strategy Under Unbalanced Grid Voltage

LI Zhengguo1, SUN Xiaoli1, MENG Fankun1,2

（）

In order to ensure a safe and reliable running of the grid rectifier in power system, it is a basic requirement that the phase and frequency of the positive sequence fundamental component of the grid voltage should be obtained quickly and accurately. To solve the problem of non-characteristic harmonics caused by rectifier with unbalanced and distorted voltage, a method based on the single synchronous reference frame was put forward to detect the positive and negative sequence components of unbalanced grid voltage by double dq transformation and decoupling calculation. The simulation results verified the validity and the effectiveness of the method under the unbalanced and distorted grid voltage as well as the sudden change of grid voltage frequency.

decoupling control; unbalanced voltage; double synchronous reference frame(DSRF)

10.13899/j.cnki.szptxb.2019.05.001

2019-05-13

国家自然科学基金资助项目（51707014）

李正国（1972-），男，湖南汨罗人，教授，博士，研究方向为电力电子控制理论与应用．

TP202

A

1672-0318（2019）05-0003-06