利用白光数字图像频域分析法测量动荷载作用下有砟轨道的下沉量

战启芳， 杜立峰， 杨新伟， 万 涛， 程 佳， 王素康

(1. 石家庄铁路职业技术学院 铁道工程系 河北 石家庄 050041; 2. 北京交通大学 土木建筑工程学院， 北京 100044)

在高速列车荷载的作用下，铁路线路的轨道结构会发生不均匀的沉降变形，造成轨道结构几何形位偏差，会引起整体线路的不平顺。在列车动荷载的反复作用下，这种不平顺会逐渐加强，最终铁路轨道的结构功能被破坏。这种轨道结构的破坏就叫做轨道下沉破坏。由于轨道的下沉破坏大都为道床的下沉破坏，所以也被称为道床下沉破坏。

目前，研究道床下沉的方法有试验研究和仿真分析这两种方法。第一种是通过试验或监测来研究轨道变形，得出轨道变形的经验公式；第二种方法是以试验研究为基础，利用数值仿真来研究轨道的下沉，从理论上为轨道的下沉提供了帮助的参考[1-3]。

20世纪50年代，日本建立了轨道下沉破坏理论[4]，其中为代表的是星野和佐藤(裕)的“最佳轨道结构理论”和以崛越小野的“轨道承载力理论”[5]，最后由佐藤吉彦总结并发展了这些理论，形成了新轨道破坏理论。以此为基础，后续几十年里，研究者们进一步地研究和发展轨道下沉破坏理论[6-8]。

而测量轨道下沉的实验方法主要有以下几种：

(1) 借助测量道床下沉的测试仪器来测量道床的下沉[9]，主要包括测试仪器、数据采集仪器、各类传感器。此种测量方法所用仪器较多，所需测量物理量较多，因此测压力点众多；将试验设备安装在轨道上，当列车通过时，一部分的加速度仪可能会损坏，故不能将此方法用于实际的轨道下沉检测中。

(2) 基于全站仪和轨检小车的轨道检测系统[10]。这种测量方法其移动性不强，设备成本高昂，难以满足我国当前轨道平顺性(包括道床下沉)的巨大检测数据的需要；用全站仪进行动态位移测量的测量速度远远不能满足结构动态测量的需要。

(3) GPS卫星测量法[11]。具有全天候、自动化、点间无需通视、精度高的特点，但是这一技术对接受天线的环境要求严格、测量速率低、成本高且要求高水平专业人员，推广应用于大型土木结构的可能性较小。

(4) 数字摄影测量法[12]，通过数码摄像机来获取图像，利用计算机处理图像信息。数字摄影测量可用来检测轨道几何平顺性，及测量道床的下沉，但数字摄影测量一般是通过专业摄影测量系统，将其用于道床的下沉检测，不论是其硬件还是软件系统都有待科研人员做进一步的交叉研究和开发。

由于轨道下沉的相关测量方法精度低、操作复杂、测量成本高。因此，亟待引进一种新的测量方法，能够克服以上缺点来推动轨道下沉检测技术的进步。

白光数字图像频域分析法[13-14]是一种测量物体位移与变形的数字图像类的实验方法。该方法是通过CCD摄像机拍摄被测物体变形前后或运动前后的图像，将拍摄的图像输入计算机，将其数字化，以被测物表面随机分布的灰度函数为计算对象，将图像进行傅里叶变换，在频域中求得位移信息。该方法已经发展了逐点分析法和全场分析法，特别是引入相移法之后，能进行全自动测量。该方法的测试操作系统非常简单，并且不需要对被测物的表面进行散斑化的特殊处理，对光强的要求也低，且能测量半透明物体的位移与变形。因此，与其他的数字图像相关法比较，其应用范围更广泛。白光数字图像频域分析法具有光路简单，操作方便，能利用CCD摄像机进行近程和远程测量，测量精度高，能达0.05像素，测量成本低等优点。

本文借鉴文献[1]对道床结构的研究，利用车辆-轨道耦合动力学理论和道床累积下沉模型，引入白光数字图像频域分析法测量轨道的下沉量，并分析不同速度列车对道床下沉变形的影响，并与文献[1]的研究成果进行对比，得出该方法在测量轨道结构的下沉是否合理。将白光数字图像频域分析法引入到有砟轨道下沉量的测试当中，能克服传统方法的缺点，推动铁路检测技术的进步。

1 白光数字图像频域分析法原理

对于图像中的一个微小的区域，可以将该区域内每点的位移看做是相同的。对小区域的图像直接进行傅里叶变换，可以得到频谱，将频谱平方并除以图像尺寸就得到功率谱。利用一对δ函数来表示同一点变形前后的灰度分布，其中，δ0(x,y)为变形前的灰度函数，δ1(x,y)为相应的变形后的灰度函数，因此有：δ1(x,y)=δ0(x+u，y+v)，见图1。

该点的位移方向与x轴夹角为θ，位移大小用d来表示，设g为该点变形前后光强之和，即

g(x,y)=δ0(x,y)+δ0(x+dcosθ,y+dsinθ)

( 1 )

对式( 1 )进行一次傅里叶变换，得到其频谱为

G(X,Y)=G0(Xf,Yf){1+exp[i2π(uX+vY)]}=

2G0(X,Y)[1+exp(-i2πxd)]

( 2 )

式中：

G0(X,Y)=

∬δ0(x,y)exp[-i2π(xX+yY)]dxdy=1

(x,y),(X,Y)为该点在物平面和谱平面的坐标；δ0(x,y)和G0(X,Y)分别为该点的散斑图在变形前的灰度分布及其傅里叶变换；x,d分别为该点在谱平面上的位置矢量和位移矢量。

式( 2 )谱平面上的光强分布可表示为

I=G*G=4cos2[π(r·d)]

( 3 )

从式( 3 )可以得到，当π(r·d)=nπ时，I最大，当π(r·d)=(n-1/2)π时，I最小。即如果以图像的形式表示，会是一系列平行条纹。

( 4 )

n=0,±1,±2,…

再分析相邻条纹间距的含义，以N和N′=N+1代表相邻的条纹级数，在小区域内认为位移是常数，式( 4 )可写成rN·d=N，rN+1·d=N+1,rN和rN+1是在谱平面的位置，相减可得d=(N+1)-N)/(rN+1-rN)即

( 5 )

式中：d为竖向像素位移值。

利用式(5)可求出位移值，Δr为相邻条纹间距。

令M为CCD摄像机的成像放大系数，则实际位移D为

( 6 )

根据域变换理论

( 7 )

式中：Lccd为相机的靶面尺寸；ΔK是相邻条纹间隔的像素值。

联立式( 7 )和式( 6 )，可得

( 8 )

该方法可以在数秒钟内在电脑中计算出功率谱，进一步根据条纹间隔大小计算出位移值。

利用白光数字图像频域分析法，可以测量出当列车经过时，轨道下沉区域的位移，利用被测区域的位移信息，求出该区域的形变。进一步，根据文献[1]中的道床累计变形模型，求出道床累计下沉率。

2 实验装置和实验过程

2.1 实验装置

一个CCD相机，相机支架，一台装有视频录制软件的笔记本电脑。

2.2 实验过程

以京九线铁路轨道为实验对象，实验地点在河北省石家庄市桥东区太平河段的京九线路。

具体的实验步骤如下：

Step1将CCD相机安装在相机支架上，并与计算机相连。

Step2选择拍摄区域并利用粉笔标记，拍摄区域为钢轨中间区域，调整相机直到拍摄到清晰的测量区域为止。

Step3利用标尺对测量区域的大小进行标定，拍摄区域大小为73.8 mm×73.8 mm。

Step4进行图像的拍摄，调整好相机后对列车(轴重为25 t)经过前的钢轨进行拍摄、记录，在列车运行时进行拍摄、记录。

3 实验数据的处理

列车以160 km/h的速度经过钢轨前后的图像见图2。

3.1 实验照片的选取

3.2 实验照片的处理

处理图片：以整张图片的中心点为坐标原点(0，0)，在其周围取点，取步长为1像素，等差取25个点，组成一个五维的矩阵，利用matlab软件对五维的矩阵进行处理，处理得到一个光滑的三维可视图形，即为此区域的变形场。取得25个点测点分布见图3。

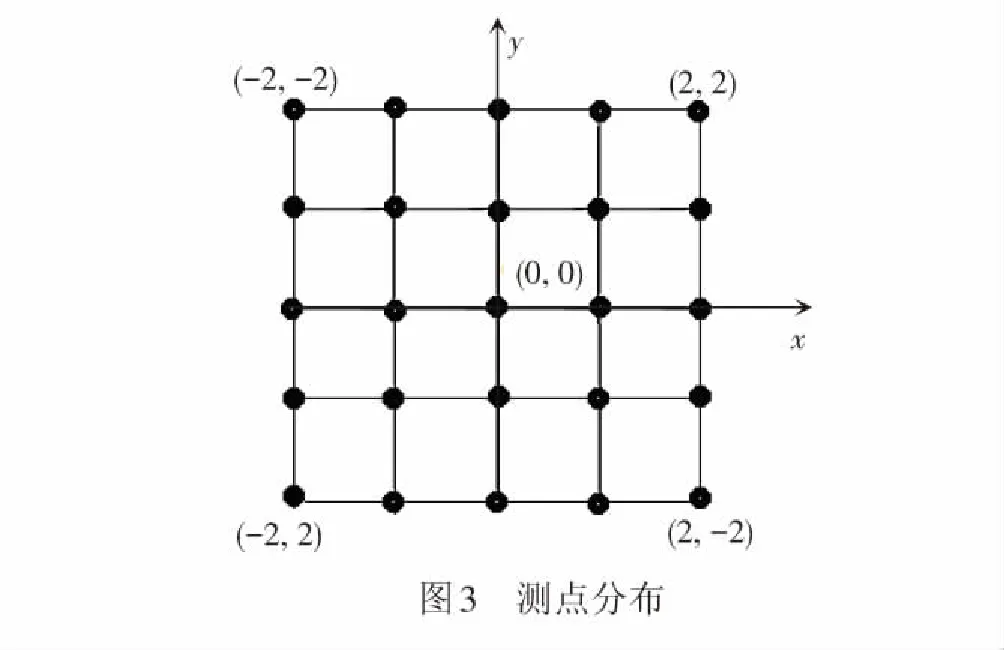
利用白光数字图像频域分析法可以得到各点的条纹图见图4，只显示部分测点的条纹图。

3.3 各点像素位移的计算

像素位移为

( 9 )

式中：Δk为条纹的像素位移；Δl为实际量测的两条纹间距，mm；512为图片的像素；73.8为照片的实际长度，mm。

(10)

(11)

式中：D为测点的实际竖向位移值，mm。

表1 测量区域各点的实际竖向位移 mm

由计算得出所取各点变形前后的像素位移，用一个的矩阵表示为

再用Matlab软件将这个五维的矩阵三维可视化，得出整个区域的变形图像，见图5。

由图5、表1可得，变形区域的形变为0.60。

3.4 道床参数的计算

基于文献[1]的道床下沉累积下沉模型和相关的试验数据，以及试验数据得出的结论，可知

(12)

式中：ε为道床应变，10-6ε；σb为道床顶面应力，MPa。

基于文献[1]给出的道床累积变形模型，可得出道床在稳定阶段累积下沉的模型为

(13)

式中：β为道床累积下沉率，mm/次；ab为道床振动加速度；σb为道床顶面应力；c为系数，根据试验和现场经验确定，取为4.09×10-7。

参考道床振动加速度方面的研究[1]，总结得出不同速度列车的道床振动加速度，见表2。

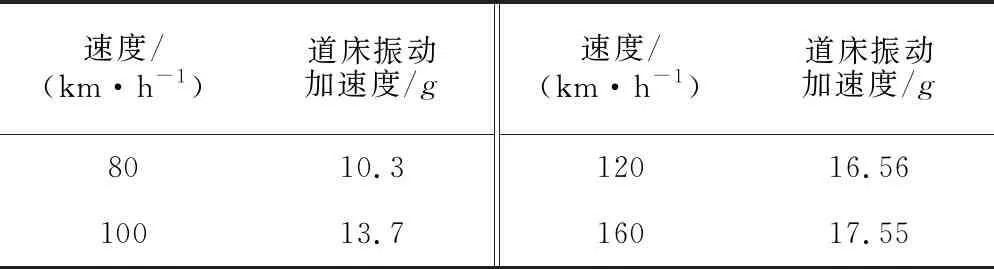
表2 不同速度列车的道床振动加速度

可计算得出，σb=0.055 MPa，β=2.46×10-6mm/次。

3.5 不同速度的列车对道床下沉的影响

通过以京九线石家庄岔河路段的有砟道床为实验对象，对不同行驶速度的列车对轨道的下沉的影响进行了观测，测量速度分别为80、100、120、160 km/h四个速度档，利用相同的方法来研究其他列车对道床沉降造成的影响。处理数据得出结果，提出道床累积沉降率的概念，分析不同速度的列车引起道床的单次下沉量问题。

列车速度分别为80、100、120 km/h时，对应的位移矩阵为A2、A3、A4，测试区域像素位移分布见图6。

由矩阵数据可得，变形区域的形变为0.524。

由矩阵数据可得，变形区域的形变为0.495。

由矩阵数据可得，变形区域的形变为0.434。

根据变形区域的形变值，可计算出不同列车速度下的道床累计下沉量，见图7。

由图7可知，当行车速度由80 km/h分别提高到100、120、160 km/h时，道床累积下沉量分别增大了171%，389%，773%。由图7可见，随着行车速度的提高，道床下沉量呈显著增大趋势。

在文献[1]中，作者结合轨道下沉模型和仿真模型，计算出来的单次列车运行下道床的最大下沉量、平均下沉量分别为9.370×10-6、4.669×10-6mm，而此方法计算得出的道床最大下沉量、平均下沉量分别是8.87×10-6、4.67×10-6mm，由于多种因素影响，实际实验结果和仿真方法分析轨道下沉总存在差异，但是两者的数量级是一致的，说明本论文的实验方法分析道床的下沉趋势是可行的，故可利用数字图像相关法来测量轨道结构下沉的下沉量。

由图7可知，在列车动荷载作用下，随着列车速度的提高，道床的下沉量也相应地提高，但单次荷载作用下道床的下沉量相差不大，可以预测当荷载作用次数超过100 000次后道床的下沉量才比较明显。根据铁运〔2006〕146号 《铁路线路修理规则》[15]中的道床下沉量标准，当道床的下沉量超过4 mm，就必须对道床进行维修。因此利用图7，可以初步估计不同行车速度和循环次数产生的道床下沉量，为道床的维修提供一定的预测参考。

4 结束语

本文基于车辆-轨道耦合动力学理论和轨道下沉变形法则，利用白光数字图像频域分析法测量有砟轨道在列车动荷载作用下的下沉量，并分析不同速度列车对道床下沉变形的影响。利用白光数字图像频域分析法测量道床的下沉量与理论计算的道床下沉量相进行比较，相差较小。与文献[1]的实验结果做对比，可以看出，本论文所得试验数据结果同文献[1]研究所得的结果相差较小，所得实验结论与文献[1]所得结论相同。故可利用数字图像相关法来对轨道的下沉进行观测。