基于热效应的含点蚀故障的齿轮啮合特性分析

2019-10-18王成烨

重型机械 2019年5期

王成烨，刘杰

(沈阳工业大学机械工程学院，辽宁沈阳 110870)

0 前言

齿轮传动系统是机械系统当中最重要的传动系统。其中点蚀是齿轮最为常见的失效形式。当齿轮齿面存在点蚀现象时，齿轮在传动过程中的有效接触面积减少，使得齿轮传动系统承载能力降低，如果点蚀面积过大导致了齿轮轮齿刚度低于最低刚度要求，轮齿会出现断裂，这将导致整个机器出现故障甚至报废。所以对含点蚀故障齿轮传动特性研究具有重要意义。齿轮在传动时，由于啮合过程中的摩擦会产生一定热量，这将导致齿轮出现一定程度的热变形，使齿轮传动出现误差。所以，在分析点蚀对齿轮啮合刚度的影响时考虑热效应会使分析结果更加精确。

目前，国内外很多学者对齿轮点蚀故障以及齿轮热效应问题进行了研究。Wang[1]利用ANSYS软件建立单对齿轮轮齿模型，分析了单对轮齿的啮合刚度，为含点蚀缺陷齿轮啮合特性的研究打下基础。Chaari等[2]建立一对三维的齿轮啮合模型，推导了时变齿轮啮合刚度的解析表达式，提供了一种求解啮合刚度值的方法。赵丽娟等[3]结合工程实际，以采煤机的摇臂传动系统为例，运用有限元方法分析了不同程度齿面磨损的齿轮啮合时的接触应力。刘杰等[4]将齿轮轮齿简化成悬臂梁模型，计算包含太阳轮齿根发生裂纹故障时系统的时变啮合刚度，对含故障齿轮啮合刚度研究有重要意义，也使得点蚀故障齿轮啮合特性的研究更近一步。C.K. Tan等[5]利用声发射(AE)技术对直齿圆柱齿轮进行了点蚀失效的试验研究，分析出齿轮齿面上的节线附近更易产生点蚀，这一结论为研究点蚀齿轮啮合刚度中点蚀的位置这一问题的研究有很大意义。安春雷等[6]建立了含点蚀缺陷的齿轮模型，利用MATLAB比较了有点蚀与无点蚀剥落齿轮的扭转啮合刚度的变化情况。Yaguo Lei等[7]运用正态分布函数沿齿宽方向建立点蚀模型，分析了含点蚀故障齿轮的时变啮合刚度。Xihui Liang等[8]计算出不同程度的点蚀齿轮对应的齿轮啮合刚度，并对比了齿轮在不同程度点蚀时齿轮啮合刚度的变化趋势。陈长征等[9]结合传热学、摩擦学等理论，求解出单个齿轮轮齿的稳态温度场，为齿轮热效应研究提供帮助。

目前很多学者对齿轮故障问题进行了研究，但是大多数学者在对齿轮啮合特性以及齿轮故障问题研究时没有考虑到齿轮温度变化对其啮合特性的影响。由于齿轮在啮合过程中因摩擦而产生热量，轮齿温度因此升高，可能会对齿轮的啮合特性产生影响。虽然一些学者对齿轮热效应进行了研究，但是只是局限于研究齿轮热效应问题，并未对含点蚀故障的齿轮进行研究。本文运用ANSYS模拟出带有不同程度点蚀的齿轮温度场，分析齿轮温度分布规律以及不同程度点蚀对齿轮温度场的影响。同时计算不同点蚀面积以及是否考虑受热的啮合刚度，通过对比分析出点蚀以及温度场对齿轮啮合刚度的影响规律。由于目前对点蚀的不同程度并没有一个明确的界定，所以本文根据工程实际情况将点蚀分为轻度、中度和重度，并对这三种程度的点蚀做了一个界定。

1 齿轮温度场分析

1.1 齿轮热力学分析边界条件

通过热力学定律可以分析出瞬态温度场的场变量应该满足的微分方程[9]如下：

(1)

对式(1)求解所需要的边界条件为

(2)

(3)

(4)

式中，ρ为材料密度；C为比热容；λ为导热系数φ；为内热源；hm、ht和hs分别为齿轮工作面、非工作面和端面的对流换热系数；Q为齿轮啮合时摩擦产生热量；T0为初始温度；T为轮齿温度。

1.1.1 对流换热系数

由于对流换热系数的影响因素较多，目前只有通过理论公式进行近似计算。本文采用的润滑油参数如表1所示。

表1 润滑油参数

(1)齿轮端面对流换热系数计算。经计算可得雷诺数Re≤2×102，故对流换热系数为

(5)

式中，Pr为普朗特系数，其中ρf、cf、vf和λf分别为润滑油密度、比热容、粘度和导热系数；Kf为润滑油导热系数；ω为齿轮角速度；m为指数常数，当温度沿径向分布时取m=2[9]。

(2)齿轮啮合面换热系数计算。齿轮啮合面换热系数计算为

(6)

(3)齿根和齿顶面换热系数计算。齿根面和齿顶面的对流换热系数可以简化处理为齿轮啮合面对流换热系数的1/3[9]。

1.1.2 齿轮摩擦热流量计算

(1)相对滑动速度。主、从动轮啮合的接触点对沿接触切线相对滑动速度计算为

(7)

(8)

(9)

式中，n1、n2分别为主、从动轮转速；d1、d2分别为主、从动直径；ds为啮合点与节点沿啮合线上的距离；α为齿轮压力角，本文齿轮压力角α=20°；vs1、vs2分别为主、从动轮滑动速度。

(2)齿面摩擦系数。

(10)

式中，Ft为齿轮啮合点切向载荷；Xr为齿面粗糙度因子；ρe为齿轮等效曲率半径；b为齿宽。

(3)齿面接触压力。基于Hertz理论，齿面接触压力为

(11)

式中，Fs为齿面法向载荷；E为综合弹性模量。

1.2 齿轮温度场有限元分析

1.2.1 健康齿轮稳态温度场有限元分析

本文运用有限元方法建立齿轮轮齿单齿模型，在轮齿不同面施加对应的热边界条件。齿轮参数如表2所示。

表2 齿轮副基本参数

本文通过对主动轮单个轮齿的稳态温度场分析来反映整个齿轮轮齿的状况，温度分布情况如图1、图2、图3所示。

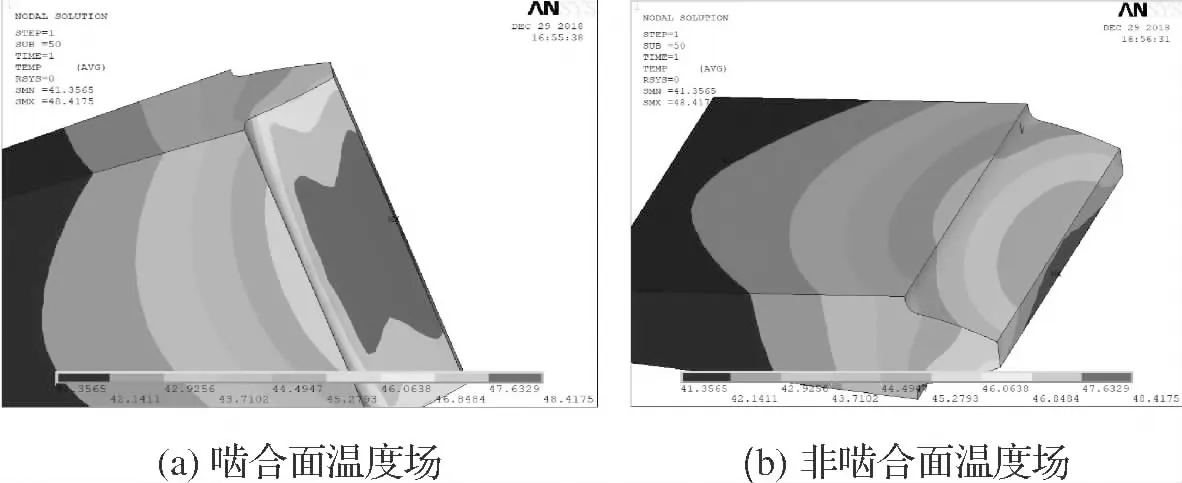
图1 单齿稳态温度场

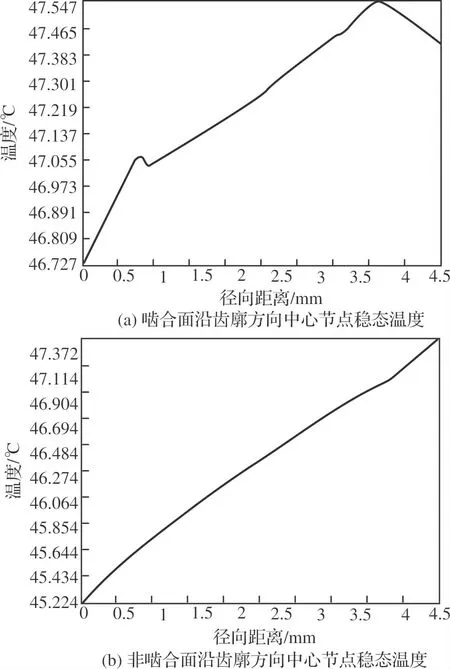
图2 沿齿廓方向稳态温度

从图1可以看出，无论是啮合面还是非啮合面，齿轮轮齿的齿顶处都是最高温度区。这是由于相比于齿根处和节圆处，齿顶参与啮合的时间更长，摩擦更多，导致因摩擦产生的热量更多。非啮合面的温度要低于啮合面，这是由于非啮合面热量主要来源于啮合面摩擦热的热传导。从图2a可以看出齿顶温度总体上高于齿根温度；但是靠近齿根处温度有小幅下降，齿顶靠近末端温度开始下降。这是由于齿根处散热条件较差，加上节圆处的热传导作用导致齿根靠近节圆附近出现局部温度较高的现象。从图2b可以明显看出非啮合面齿顶温度高于齿根温度，因为齿轮轮齿非啮合面的热量主要来自于啮合面产生的经热传导作用传递过来的热量，而啮合面齿顶温度较高，加之直齿圆柱齿轮齿顶厚度薄于齿根，导致齿顶温度高于齿根。从图3可以看出，沿齿宽方向越靠近外侧温度越低，因为轮齿外侧散热条件好于内侧。

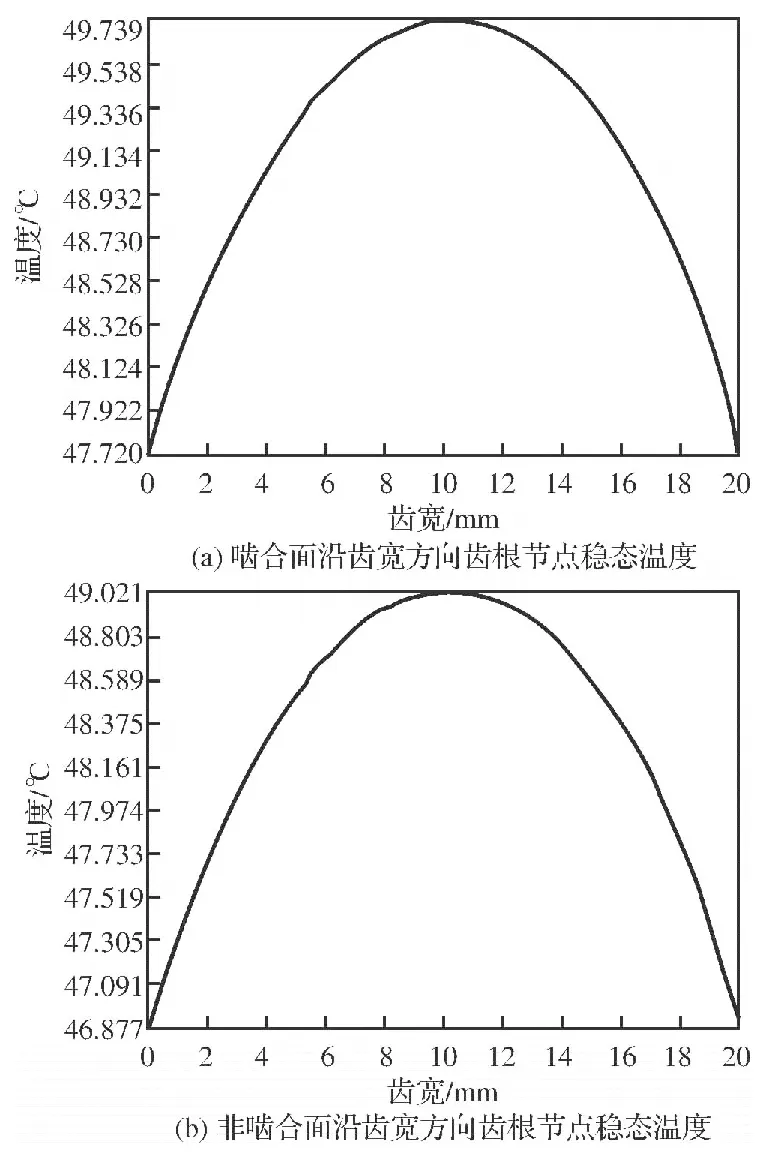
图3 沿齿宽方向稳态温度

1.2.2 含点蚀故障齿轮稳态温度场有限元分析

本文在主动轮上建立出圆形凹坑，半径和深度均为0.5 mm，以此来模拟出主动轮上的点蚀故障。本文主要研究的是主动轮的点蚀故障，所以对从动轮不做点蚀故障模拟。坑的数量是不同的，以模拟不同程度的点蚀故障。

点蚀一般在节线周围开始，然后传播到整个齿轮表面。一个坑的位置和大小可以用三个变量来表示(u，r，D)，其中u代表齿根到点蚀坑中心的距离，r是点蚀坑的半径，D是点蚀深度。齿数为55的齿轮经过计算可知节线到齿根距离为2.5 mm，而本文模拟的点蚀坑中心在节线上，所以设定u=2.5 mm，r=0.5 mm，D=0.5 mm。

本文将点蚀程度分为三个等级，将点蚀面积在10%以下定义为轻度，将点蚀面积在10%到30%之间定义为中度，点蚀面积在30%以上定义为重度。根据界定范围，本文模拟出三种点蚀程度的齿轮模型。

轻微点蚀：以齿节线为中心在齿面上模拟出10个圆形凹坑，每个点蚀坑中心距为0.75 mm。该齿的点蚀面积为轮齿表面积的7.59%。齿表面积为90 mm2。

中度点蚀：以齿节线为中心在齿面上模拟出22个圆形凹坑，每个点蚀坑中心距为0.75 mm。点蚀面积占齿表面积的16.55%。

重度点蚀：以齿节线为中心在齿面上模拟出22个圆形凹坑，另有22个凹坑位于齿顶，每个点蚀坑中心距为0.75 mm，两排点蚀坑之间的中心距为1 mm。点蚀面积占轮齿表面积的33.1%。

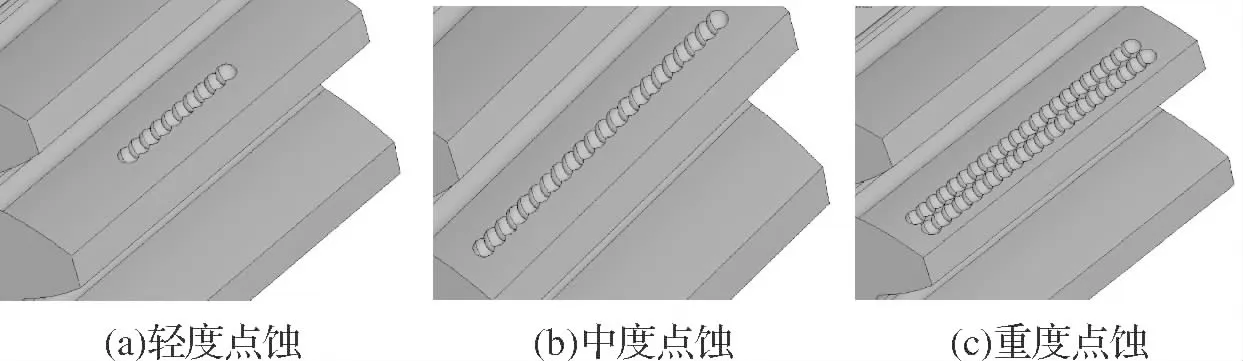
图4 不同程度点蚀齿轮模型

图4给出了三种程度点蚀齿轮轮齿模型。图5及图6给出了不同程度点蚀单齿的稳态温度场情况。

从图5可以看出，点蚀面积的大小对齿轮的温度场分布具有一定程度的影响。对比图5a与图5b可以发现，轻度和中度点蚀轮齿最低温度分别为43.422 ℃和43.451 ℃，最高温度分别为50.27 ℃和50.34 ℃。从云图以及数据中可以看出，点蚀面积沿齿宽方向扩大，齿轮温度场并无明显变化。从图5c可以看到，重度点蚀轮齿最高温度52.03 ℃，最低温度43.82 ℃。通过与图5b的对比可以看出点蚀面积沿齿廓方向扩大，温度分布出现明显变化，且温度也明显升高。由于齿轮传动过程中，齿面之间的摩擦是沿齿廓方向径向摩擦，这使得齿轮轮齿之间沿齿宽方向几乎没有摩擦热流量，所以温度场分布几乎不会受到影响。当点蚀面积沿着齿廓方向扩大时，轮齿节线附件摩擦热流量减小，导致齿轮节线附近温度降低，热量更多地集中到齿顶方向。

图6a～图6c为啮合面温度分布情况，可以看出，齿轮出现点蚀故障后，由于齿轮节线处出现点蚀坑，使得该处空气流通较好，更易散热，因此在节线附近点蚀位置温度出现下降。齿顶附近相对滑动速度大，导致齿顶温度依然很高，且越靠近齿顶温度越高。图6d～图6f为非啮合面温度分布情况，可以看出，齿顶温度高于齿根温度，但齿顶最外侧温度小幅降低，因为非啮合面齿顶最外侧散热条件好，使得最外侧温度会略低于齿顶稍靠内侧处。

图5 点蚀齿轮啮合面稳态温度场

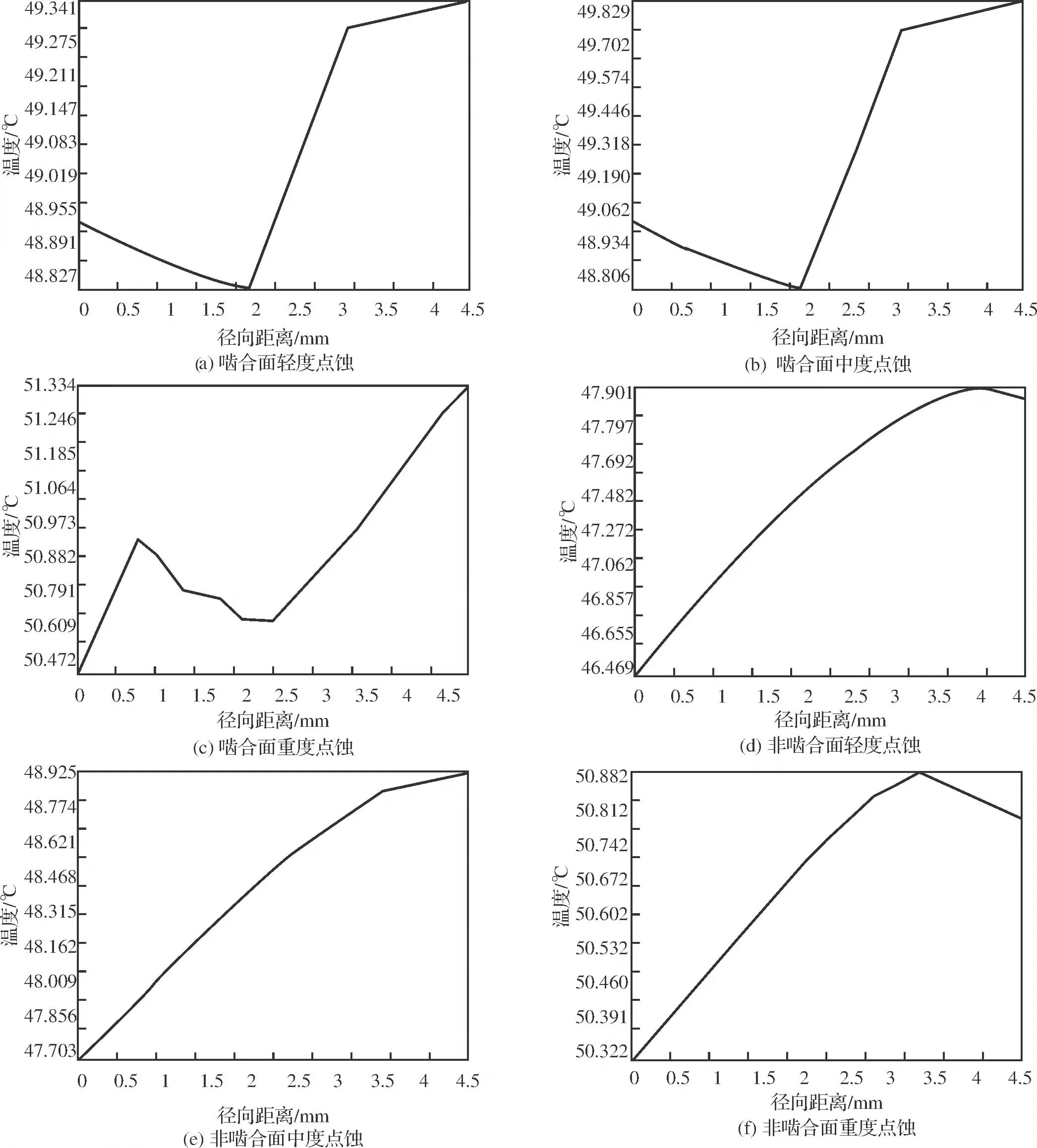
图6 点蚀齿轮沿齿廓方向稳态温度

不同程度的点蚀对齿轮总体温度有一定程度的影响，但是影响效果不是很明显。沿齿廓方向齿顶附近温度最高；沿齿宽方向中心温度高于两侧温度。

2 齿轮啮合刚度分析

2.1 有限元啮合刚度求解方法

齿轮的啮合刚度反应出了齿轮工作时抗变形的能力。轮齿的啮合刚度值K为[10]

(12)

式中，Fn为啮合点的法向力；B为轮齿齿宽；δ为沿啮合线的线性变形。

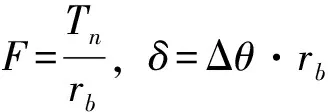
(13)

式中，Tn为齿轮转矩；Δθ为主动轮转角；rb为主动轮基圆半径。

2.2 不考虑热效应的齿轮啮合刚度研究

2.2.1 健康齿轮啮合刚度分析

运用有限元软件建立齿轮模型，在求解过程中，假设双齿刚开始进入啮合位置的主动轮转角为0°，齿轮的重合度为1.794，那么通过计算可得这一对啮合齿轮双齿啮合区间为主动轮转角0°～5.198°和6.544°～11.743°，单齿啮合区间为5.198°～6.544°，当扭矩T=60 N·m的情况下，求得啮合刚度，结果如图7蓝色线所示。

2.2.2 点蚀齿轮啮合刚度分析

计算含点蚀故障齿轮啮合刚度方法与健康齿轮啮合刚度计算方法相同。定义当主动轮含点蚀的轮齿与对应从动轮轮齿刚刚接触时主动轮的角位移为0°，当主动轮旋转到3.45°时点蚀坑开始进入啮合区域；在轻度和中度点蚀啮合过程中主动轮旋转到6.9°时点蚀区离开啮合区域，重度点蚀齿轮则是主动轮旋转到11.2°时点蚀区脱离啮合。啮合刚度计算结果如图7所示。

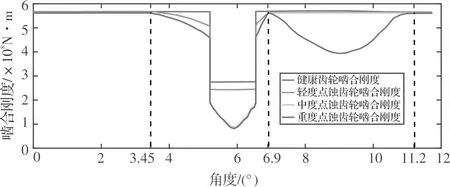
图7 不同程度点蚀齿轮啮合刚度

从图7中可以看出，点蚀面积越大，齿轮的啮合刚度下降越大。为了量化点蚀对齿轮啮合刚度的影响，本文将啮合过程分为三个阶段。第一阶段为主动轮旋转角度从0°～3.45°，此时点蚀区域未参与啮合；第二阶段主动轮旋转角度从3.45°～6.9°，此时节线上的点蚀区进入到了啮合区域；第三阶段为主动轮转角从6.9°～11.2°，此时节线上的点蚀区离开啮合区域，重度点蚀齿轮的齿顶附近点蚀坑进入啮合。在每个阶段，通过计算并对比各阶段的啮合刚度，可以得出不同点蚀程度在不同阶段齿轮啮合刚度的下降程度。在第一阶段，三种程度点蚀齿轮的啮合刚度均无明显变化；到了第二阶段，轻微点蚀齿轮啮合刚度下降比例约为10.5%，中度和重度点蚀齿轮啮合刚度下降比例大约35.1%；到了第三阶段，轻度和中度点蚀齿轮啮合刚度下降在1%左右，而重度点蚀齿轮则下降大约18%。

2.3 考虑温度场的齿轮啮合刚度研究

通过有限元法计算考虑热分析的含点蚀故障齿轮啮合刚度，需要在加载过程中将热边界条件加载到对应的面上。对考虑热效应和未考虑热效应的健康齿轮啮合刚度进行对比，并在加入热载荷的情况下对不同程度点蚀的齿轮进行啮合刚度分析，研究结果如图8、图9所示。

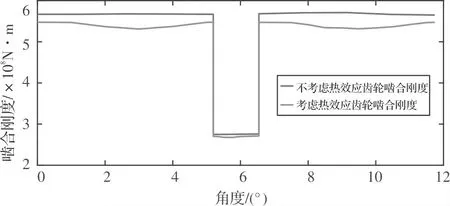
图8 健康齿轮考虑热效应及不考虑热效应啮合刚度对比

图9 考虑热效应的不同程度点蚀齿轮啮合刚度

从图8可以看出，考虑到齿轮啮合时摩擦产生热量这一初始条件后，齿轮轮齿出现了一定程度的热变形，使齿轮轮齿啮合刚度出现降低。由于单双齿啮合特点不同，啮合刚度下降幅度有一定差别，双齿啮合区下降比例在4%～4.5%，单齿啮合区下降比例大约为0.5% 。由于考虑到温度导致啮合时应力分布不均匀，双齿啮合区中部啮合刚度值出现下凹现象。

从图9可以看出，考虑热效应后不同程度点蚀啮合刚度变化趋势上与不考虑热效应的啮合刚度变化趋势基本相同，但双齿啮合区中部啮合刚度值均出现下凹现象。而不同程度点蚀啮合刚度值有一定程度下降，健康和轻度点蚀啮合刚度值下降4%左右，中度和重度点蚀啮合刚度下降大约4.5%。