复杂地形下TRMM降水数据的降尺度研究：以四川省为例*

李 豪，雷 苑

复杂地形下TRMM降水数据的降尺度研究：以四川省为例*

李 豪，雷 苑

（四川农业大学资源学院，成都 611130）

TRMM数据是目前应用最广泛的卫星降水产品，其准确性已得到广泛验证和认可。但其相对较低的空间分辨率制约和阻碍了在各领域的进一步应用。本研究以降水空间分异显著的四川省为例，在综合考虑空间位置、地形等多个影响因素及其空间非平稳性特征的基础上，采用混合地理加权回归（MGWR）与克里格插值（Kriging）相结合的方法，建立一个兼顾多因素空间非平稳性特征的降尺度模型（MGWRK），对研究区域的TRMM年降水数据进行降尺度研究，并通过41个气象站点的实测数据对不同降尺度方法的结果进行对比验证。结果表明：（1）经过降尺度处理后，TRMM降水数据的空间分辨率从0.25°（约26km）提升至1km，数据的精细程度有了明显提升；（2）MGWRK模型综合运用了空间位置、地形等多个高分辨率的辅助信息，并进一步探究了不同影响因素对TRMM降水影响关系的空间非平稳性类型与特征。从多年平均及两个典型年份的验证结果看，MGWRK法比传统的重采样方法Bilinear法及基于OLS的全局回归克里格法具有更高的精度，降尺度结果的精度更接近TRMM原始数据；（3）构建的降尺度模型兼顾了提升空间分辨率和保持数据精确度两方面的要求，适用于四川省TRMM降水数据的降尺度研究，可为TRMM数据在小尺度的应用研究提供有效的数据支持。

TRMM降水数据；降尺度；混合地理加权回归；四川省

降水作为全球大气和水循环的关键环节和最为活跃的要素，在气象、农业和环境等研究领域具有重要意义，可为农业生产、水资源管理、防洪减灾、生态环境治理等提供有效的数据支持[1−2]。利用卫星遥感获取降水数据，具有测量范围广、分布连续、现势性强和精度高等优势[3−5]，目前已成为区域降水数据的重要来源。近年来，随着研究工作的深入，各领域对降水数据在空间尺度上的精细化需求也不断提高。

TRMM（Tropical Rainfall Measuring Mission，热带降雨测量任务）由美国国家宇航局和日本宇宙开发事业团联合研制，是第一部搭载主动式监测降水雷达的遥感卫星[6−7]。自1997年11月发射以来，TRMM已经连续提供了20余年全球中低纬度范围的降水数据，是目前应用最广泛的卫星降水产品，其准确性得到了广泛验证和认可[8−11]。但不可忽视的是，TRMM数据的空间分辨率相对较低（最高为0.25°×0.25°），在中国大部分地区其分辨率仅有20多km，小区域、细节性的降水空间分布特征容易被掩盖，在部分下垫面较复杂的地区该问题显得更为突出，无法完全满足小尺度研究对降水数据的精细度要求。对TRMM数据进行降尺度处理，提高空间分辨率是扩大其应用范围的必由之路。

近年来，对TRMM数据的降尺度处理已成为国内外研究的热点之一。目前，TRMM降尺度研究主要采用“回归分析+空间插值”方法，即首先通过建立TRMM降水数据与相关影响因素（如空间位置、地形、植被指数等）间的回归关系函数获取高分辨率的回归趋势面，然后采用克里格、样条函数等空间插值方法对回归残差点数据进行插值，然后叠加回归趋势面与残差面数据，从而获得较高空间分辨率的降水数据。已有研究表明，该方法可以在提高TRMM降水数据空间分辨率的基础上，同时保持较高精准度[12−19]。

然而，相关研究仍存在一些不足之处：一方面区域降水的空间分布往往受空间位置、地形等诸多因素影响，部分研究仅选取一个影响因素（多为植被指数）进行分析，往往无法全面刻画降水和各因素间的相互关系；另一方面大部分研究采用基于最小二乘法（Ordinary Least Square，OLS）的全局回归模型进行回归分析，没有考虑影响因素变量的空间非平稳性特征，这些问题都导致经过降尺度处理后的TRMM数据精度仍受到一定的限制。

为此，本研究以TRMM降水与多个主要影响因素间的相互关系及其空间非平稳性特征为切入点，尝试采用混合地理加权回归（Mixed Geographically Weighted Regression，MGWR）+克里格插值（Kriging）的分析模型在地形复杂多样、降水空间分异显著的四川省开展TRMM年降水数据的空间降尺度研究，并与全局回归克里格、双线性内插等以往研究方法的结果进行对比分析，探寻适合本区域的TRMM数据空间降尺度方法，以期获得兼顾精细化与准确性的区域降水数据，为开展农业产业结构调整、水资源优化配置、生态环境治理等工作提供有效的数据支持。

1 资料与方法

1.1 数据来源

研究数据包括TRMM 3B43降水数据、气象站实测降水数据和研究区数字高程模型（Digital Elevation Model，DEM）数据。

TRMM降水数据由美国国家航空航天局（NASA）提供（https://mirador.gsfc.nasa.gov/），使用第7版3级（3B43-V7）月降水数据，空间分辨率0.25°×0.25°，时间段为1998−2017年共20a，逐月累加获得格点历年TRMM降水数据，境内各年格点数据取平均值得到四川省多年年均降水数据。已有研究表明，该TRMM降水数据在四川地区具有较高的预测精度[9]。

同期四川省（92°21′−108°12′E，26°03′−34°19′N）41个气象站的年降水量（观测精度为0.1mm）、经纬度等数据来自中国气象数据网（http://data.cma.cn）的“中国地面气候资料年值数据集”。研究范围及各气象站点的空间分布如图1所示。研究区域的DEM数据来源于NASA空间科学数据中心提供的SRTM3 V4数据（http://srtm.csi.cgiar.org/），空间分辨率为90m，在进行降尺度研究前首先将该DEM数据重采样至1km空间分辨率。其它衍生地形数据（坡度、地形起伏度等）通过1km分辨率的DEM数据在ArcGIS软件中生成。

图1 研究区域DEM及41个气象站点分布

1.2 降尺度方法

引入表达空间位置的经度、纬度，以及表达地形的海拔、坡度、坡向和地形起伏度共6个辅助变量作为影响因素，采用混合地理加权回归（MGWR）和克里格（Kriging）插值相结合的方法对四川省TRMM年降水数据进行降尺度转换。

步骤为：（1）分析区域TRMM年降水量（空间分辨率0.25°×0.25°，目标变量）与各影响因素间（空间分辨率1km×1km）的相关系数，采用逐步线性回归法（Stepwise Linear Regression，SLR）筛选出解释变量集；（2）以TRMM年降水为因变量，以筛选的影响因素集为解释变量，采用MGWR法进行回归分析，根据回归系数的计算结果获得高分辨率（1 km×1 km）回归趋势面空间数据；（3）采用普通克里格法（Ordinary Kriging，OK）对回归残差进行插值，得到残差空间数据（分辨率1km×1km）；（4）将回归趋势面和残差插值空间数据相加，最终得到1km×1km分辨率的TRMM年降水数据，实现降尺度转换。

降尺度方法的核心是MGWR模型。目前回归分析大多采用基于OLS的全局回归（Global Regression，GR）法，即假定变量间的关系具有同质性，各解释变量的回归系数在整个研究区域内为恒定的常数。由于没有考虑某些变量间关系的空间非平稳性特征，其分析结果的准确性往往受到一定限制。为此，Brunsdon和Fotheringham提出了融合OLS全局回归和地理加权回归（Geographically Weighted Regression，GWR）的MGWR模型[20]。MGWR模型的基本形式为

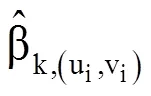
MGWR模型同时包含了OLS全局回归和GWR回归两个部分。在GWR模型中，解释变量的回归系数不再是常数，而是与空间位置有关的函数[21−22]，式（1）中，位置（ui,vi）处的回归系数β通过下式计算得到

式中，dij是样点i和j的距离，b是带宽（窗口大小），通过最小AICc（Corrected Akaike Information Criterion，修正的赤池信息量准则）法确定最佳带宽。

1.3 降尺度结果的精度评价

选择多年平均（1998−2017年）以及2个典型年份即1998年（洪涝年，20a间降水量最多，各气象站点年降水均值为1043.32mm）和2006年（干旱年，各气象站点年降水均值为780.91mm）的TRMM降水数据，分别采用混合回归克里格（MGWRK）、全局回归克里格（GRK）和双线性内插重采样法（Bilinear）3种方法进行降尺度处理，通过ArcGIS软件“值提取至点”工具获取区内41个气象站点所在位置的各降尺度结果，根据站点实测值和降尺度值计算平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、平均绝对百分误差（Mean Absolute Relative Error，MARE）、均方根相对误差（Root Mean Square Relative Error，RMSRE）和相关系数（Correlation Coefficient，R）共5个指标[23]，对不同模型的降尺度精度进行对比验证。

2 结果与分析

2.1 兼顾多因素空间非平稳性特征降尺度模型的建立

2.1.1 逐步线性回归筛选影响因子

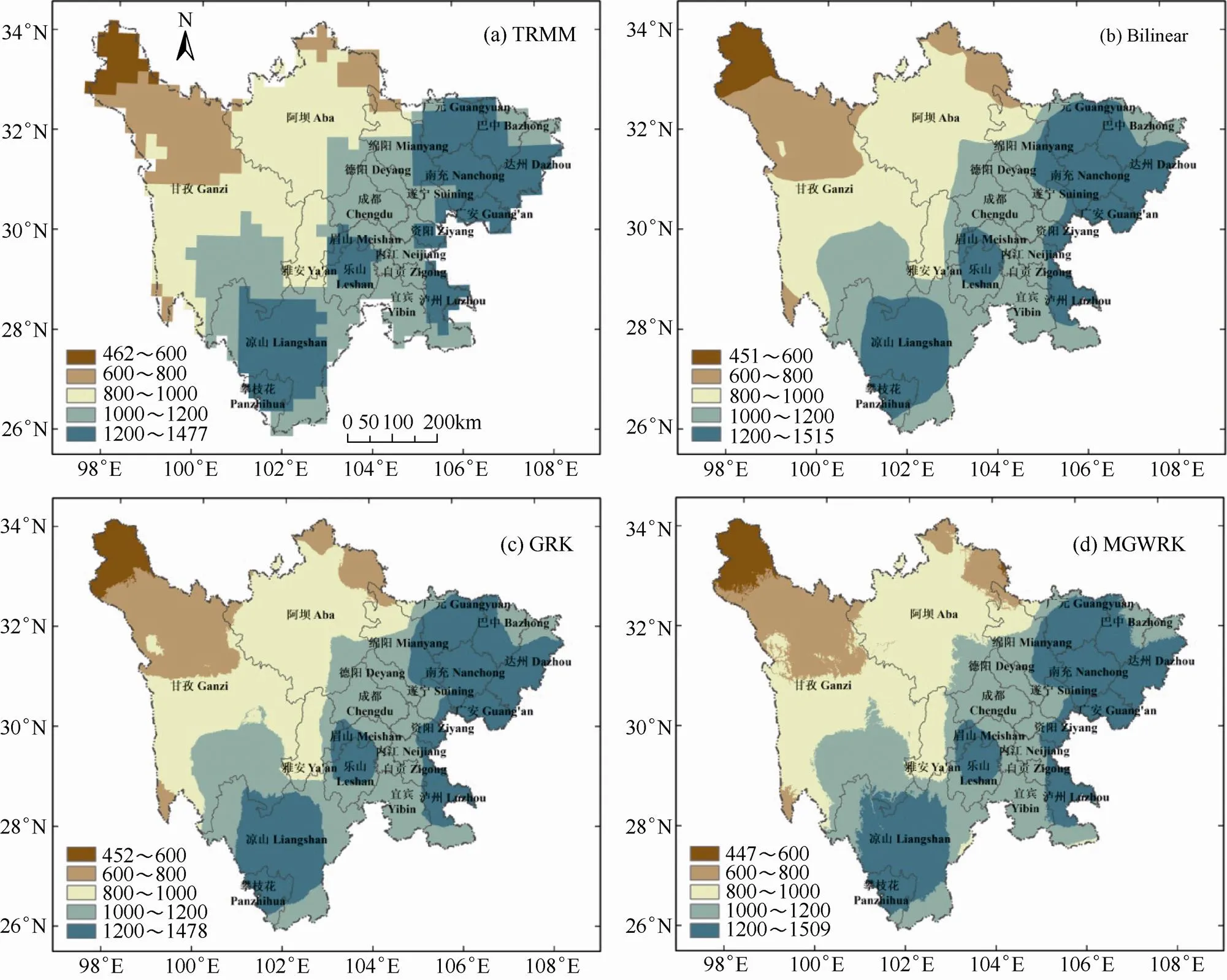
通过逐步线性回归法（SLR）可以判别并删除引起多重共线性（Multicollinearity）的变量，有效降低多重共线性程度，从而提高回归分析的准确性。首先采用SLR法分别建立0.25°×0.25°分辨率下TRMM降水多年年均值及2个典型年值与经度、纬度、海拔、坡度、坡向及地形起伏度等6个影响因素的SLR模型，并筛选出合适的影响因素变量。SLR法主要通过方差膨胀因子（Variance Inflation Factor，VIF）衡量多元线性回归模型中多重共线性的程度，一般认为当0

2.1.2 建立混合地理加权回归模型

以TRMM降水年均值及2个典型年值为因变量，SLR法筛选出来的影响因素为解释变量分别建立MGWR模型，结果见表2。

表1 不同年份格点TRMM降水数据与影响因子间逐步线性回归结果

Table 1 Results of stepwise linear regression between TRMM precipitation data and the influencing factors in different years

表2 混合地理加权回归模型（MGWR）计算结果

Table 2 Results of mixed geographically weighted regression (MGWR)

MGWR模型中包含了2种类型的解释变量：一是回归系数为常数的全局变量，M1和M2模型中，地形起伏度均为全局变量，回归系数值分别为0.0263和0.0166，说明在多年平均和洪涝年两种情况下，该变量对TRMM降水的影响在研究区域内总体上是稳定的，呈正相关关系，随着地形起伏度增大TRMM降水也随之增大；另外，在M2模型中，海拔也为全局变量，其回归系数值为0.0287，说明与起伏度类似，在洪涝年（1998年），海拔对TRMM降水的影响也为正相关关系。二是回归系数随空间位置变化的局部变量。表2结果显示，空间位置因素（即经度和纬度）是各模型的主要局部变量；此外，干旱年（2006年）与多年、洪涝年（1998年）影响TRMM降水数据的局部变量略有不同，除经度、纬度还增加了地形起伏度。

各模型局部变量回归系数的空间分布如图2所示。由于篇幅限制，以M2模型为例说明MGWR模型局部变量回归系数的空间变化特征。M2模型中的局部变量经度和纬度的回归系数空间分布如图2c所示。经度和纬度回归系数的取值范围分别在−533.54～487.74和−478.94～445.76，变异系数分别达到253.26%和−211.45%，变异程度属强变异，在整个研究区域内呈现出明显的空间变化，说明在M2模型中，经度和纬度对TRMM降水的影响具有显著的空间非平稳性，随着空间位置的变化，经度和纬度对TRMM降水的影响程度也随之变化。对于局部变量经度，除凉山东部、阿坝北部、巴中、眉山等局部地区外，其回归系数在四川省的其余区域均为正值，其中雅安、绵阳北部、广元西部等地的回归系数达到300以上；对于局部变量纬度，省内大部分区域的回归系数为负值，只有川西南的宜宾、自贡、泸州、攀枝花等地为正值，其最小值出现在川北的广元西部地区。

图2 MGWR各模型局部变量回归系数的空间分布

2.1.3 对回归残差进行克里格插值

使用GS+9软件对各回归模型的残差进行半方差函数（Semi-variogram）拟合，再根据拟合获得的步长、块金值、变程等函数参数，使用普通克里格（Ordinary Kriging，OK）法分别对各模型的回归残差进行空间插值。在此基础上，经过由影响因素变量及其回归系数叠加获得回归趋势面、回归趋势面与残差插值结果叠加等步骤，获得经过降尺度处理、空间分辨率提升为1km×1km的四川省多年平均（1998−2017年）及2个典型年（1998年和2006年）TRMM年降水空间分布图。作为对照，同时采用全局回归克里格（GRK）及重采样Bilinear法将相应年份的TRMM数据降尺度为1km×1km。

2.2 兼顾多因素空间非平稳性特征降尺度模型结果与验证

2.2.1 多年平均降水降尺度结果与验证

TRMM原始数据及各模型多年平均（1998−2017年）的降尺度结果如图3所示。由图可见，经过不同模型的降尺度处理后，TRMM降水图像的空间分辨率均有大幅改善，从原始的0.25°×0.25°（约26 km×26 km）提升至1 km×1 km。另一方面，降水空间分布与TRMM原始数据整体上保持一致；且随着空间分辨率的提高，一些小范围、局部的降水空间分布细节也更清晰地表现出来：四川省年降水的空间分布趋势大致为自西向东逐渐递增，降水峰值区除了位于全省东端的达州、巴中等地外，另一峰值区为位于四川省中部、盆地西部边缘的山前丘陵、中山区，包括雅安的名山、宝兴和乐山的峨眉山等地。这一区域即独特的“华西雨屏区”，其形成主要与地形有关，区域内西部、西北部和南部一系列山脉及东面的出口构成“喇叭”状地形，使东来的太平洋暖湿气流与盆周山地下沉的冷湿气流交汇于此，从而成为中国内陆地区降水最丰沛的地区[25]，区内各地的年降水量普遍在1300～1500mm及以上。

以41个气象站点实测数据为验证数据集，以MAE、MARE、RMSE、RMSRE和R等指标评价各模型的降尺度精度。相关系数R的值越接近1，其余评价指标的值越接近0，说明相应模型的降尺度精度越高。通过表3的分析结果可以看出，就多年平均的处理结果而言，各模型的降尺度精度由高至低为MGWRK＞GRK≈Bilinear。虽然基于OLS的GRK模型综合考虑了降水、空间位置等多个高分辨率辅助信息源，但是其降尺度精度与传统的Bilinear法相比并没有明显的提升；而MGWRK模型在全局回归分析的基础上，进一步定量描述了TRMM降水与各影响因素间相互关系的空间非平稳性特征，考虑更为周全，因此其降尺度的精度要优于GRK模型及Bilinear图像重采样法：MGWRK模型的MAE值比GRK和Bilinear模型分别降低7.16和7.69，下降率分别达7.34%和7.84%；MGWRK模型的RMSE值比GRK和Bilinear模型分别降低6.93和9.55，下降率分别达5.18%和7.00%。另一方面，从各评价指标的对比可以看出，经不同模型降尺度处理后的降水数据的精度均低于TRMM原始数据，究其原因，可能是降尺度处理虽然可有效提高降水数据空间分辨率，但本质上未能改变TRMM原始降水测量值，且处理过程中存在一定的信息损失，导致处理后的精度必然有所下降。而本研究构建的MGWRK模型的结果与TRMM原始数据最为接近，也说明该模型在提升TRMM数据空间分辨率的同时，相比其它模型可以更好保持数据的准确性，将其用于四川省TRMM年降水数据的降尺度研究是可行的。

图3 基于1998−2017年多年平均降水量不同模型的降尺度结果（mm）

注：（a）图为TRMM原数据，空间分辨率为0.25°×0.25°（约26km×26km）。（b）和（c）图分别为利用双线性内插重采样法（Bilinear）和全局回归克里格法（GRK）将TRMM数据重采样后降尺度为1km×1km的结果。（d）图为利用本文MGWR模型和普通克里格法（OK）降尺度为1km×1km的结果。下同。

Note: Figure(a) shows the original data with a spatial resolution of 0.25°×0.25° (approximate 26km×26km). Figure(b) and (c) show the TRMM downscaling results with a spatial resolution of 1km×1km by the bilinear resample technique and the GRK model, respectively. Figure(d) shows the TRMM downscaling result with a spatial resolution of 1km×1km by the model combined with MGWR and ordinary Kriging of this paper. The same as below.

表3 基于1998−2017年多年平均值的不同模型的降尺度精度分析

Table 3 Analysis of the downscaling accuracies based on long time mean of 1998−2007 of different models

Note: MAE means mean absolute error, MARE means mean absolute relative error, RMSE means root mean square error, RMSRE means root mean square relative error, and R means correlation coefficient. The same as below.

2.2.2 典型年份降水降尺度结果与验证

选取1998−2017年20a间降水量最多的1998年（各气象站点年降水均值为1043.32mm）作为洪涝年，降水量最少的2006年（各气象站点年降水均值为780.91mm）作为干旱年，采用与上述相同的3种降尺度方法进行处理，得到1998年和2006年分辨率为1km×1km的四川省降水空间分布图（图4和图5）。

由图4、图5可见，与多年平均的降尺度结果类似，2个典型年份的各模型的降尺度精度同样表现为MGWRK＞GRK≈Bilinear，GRK模型略好于Bilinear重采样法，MGWRK的降尺度效果最优。2个典型年份降水降尺度的结果同样表明，MGWRK模型较好地还原了TRMM原始资料在该地区的观测信息。

对比两个年份各模型的降尺度精度可以看出（表4、表5），洪涝年（1998年）的结果要明显优于干旱年（2006年）。如MGWRK模型的MARE和RMSRE分别从2006年的15.349%和2.122%减至1998年的8.428%和1.165%，减少了近一半，也说明不同年份TRMM数据及其降尺度处理结果的精度存在一定的差异。

2.3 MGWRK模型降尺度精度的空间分布

泰森多边形法（Thiessen Polygons）可将离散点转换为面状区域，广泛应用于研究点状数据的空间分布特征。根据各气象站点的空间分布，采用泰森多边形法将研究区域四川省分割为41个多边形，进而获得MGWRK模型降尺度残差（年降水实测值与降尺度计算值之差）的空间分布图。从图6和表6可以看出，不同年份残差的空间分布特征大致相同，除位于川西高原的理塘、甘孜、石渠，川南山地的叙永以及盆地西部山前丘陵区的雅安和峨眉山等部分站点外，四川省大部分区域的降尺度残差为负值。多年平均和2个典型年的计算结果显示，残差小于0的站点数量占比均在70%左右，面积占比也达70%以上，说明与气象站实测值相比，MGWRK模型的降尺度结果整体表现为偏高。多年平均降尺度数据的统计结果表明，残差绝对值小于100的站点共有32个，数量占比和面积占比分别为78.05%和82.22%，这与前文的分析结果一致，说明经过MGWRK模型处理后，在四川省大多数地区的降尺度结果与实测值具有较好的一致性。另一方面，位于“华西雨屏区”的2个站点即雅安和峨眉山站的残差最大，多年平均和干旱年的降水量均比气象站实测值偏低300～400mm，降尺度效果并不理想。

图4 不同模型在洪涝年（1998）的降水量降尺度结果（mm）

图5 不同模型在干旱年（2006）的降水量降尺度结果（mm）

表4 不同模型在洪涝年（1998）的降尺度精度分析

Table 4 Analysis of the downscaling accuracies by different models in the wet year of 1998

表5 不同模型在干旱年（2006）的降尺度精度分析

Table 4 Analysis of the downscaling accuracies by different models in the dry year of 2006

表6 MGWRK模型的降尺度残差分析

Table 6 Analysis of the downscaling residual by MGWRK model

3 结论与讨论

3.1 讨论

降尺度处理不能提高TRMM数据的精度。从本质上而言，TRMM降水数据的降尺度属于一种图像超分辨率（Image Super Resolution，ISR）处理[26]，即在原始低分辨率（Low-Resolution，LR）)图像的基础上重建具有清晰细节的高分辨率（High-resolution，HR）图像。通过ISR处理、分辨率提高后的图像往往会造成一定的细节失真，就本研究而言，降尺度处理后TRMM数据的精度必然有所下降。从不同模型各年份的精度验证结果也可以看出，MAE、MARE和RMSE等评价指标降尺度值均大于TRMM原始值，这与以往研究的结果基本一致[17−19]。个别指标（如1998年的MARE和RMSE）MGWRK降尺度值优于TRMM原始值，是应用残差叠加技术造成的假象，并不说明降尺度后的TRMM数据精度要高于原始数据。进行降尺度处理、提高降水数据空间分辨率的同时尽量保持原有的降水精度才是本研究的目的。本研究提出了一种基于插值的降尺度方法即MGWRK模型：通过LR的TRMM图像已知点的像元值建立拟合函数，然后由拟合函数计算、确定HR图像中未知点的值，由于在处理过程中引入了大量有用的高分辨率数据源（如空间位置、地形等），并深入分析了引入数据的空间非平稳性特征，使得重建的HR图像包含更丰富的细节信息，降尺度后数据的精度较传统的GRK和Bilinear重采样法有一定的提升，更接近原始数据的精度，能较准确地反映四川省降水分布实际状况。

降尺度结果的精度依赖于TRMM原始数据的精度。在四川地区，降水主要受地形因素影响的局地往往会出现较周围地区异常的降水分布，如雅安、峨眉山2站点位于“华西雨屏区”，该区降水主要受“喇叭”状特殊地形控制[26]，降水明显偏高，两站点的年降水量均达1500mm以上，比周围地区高500～600mm，而TRMM卫星在此区域的反演效果不佳，其原始数据与气象站点的实测数据存在较大误差；从不同年份MGWRK模型降尺度残差的空间分布可以看出，雅安、峨眉山等站点的降尺度残差较大，结果不理想。另一方面，各气象站MGWRK模型降尺度结果与原始数据的相关系数分别达到0.992（多年平均）、0.989（洪涝年）和0.984（干旱年），上述分析均表明降尺度结果的精度在很大程度上依赖于TRMM原始数据，选择精度较高的原始数据是获取高质量降尺度结果的基础，在进行降尺度前应先检验卫星降水数据在该区域的适用性。此外，从应用范围上看，本研究提出的MGWRK模型适用于年尺度的降尺度分析，但在用于月、日甚至降水事件等较小时间尺度时，由于降水分布的影响因素往往会发生变化，且部分随机性因素的作用也可能增强，因此该模型的适用性有待进一步深入研究。

3.2 结论

（1）经过降尺度处理后，TRMM降水数据的空间分辨率有了较大改善，从原始数据的0.25°（约26km）提升至1km，能够更准确地反映研究区域降水数据的空间分布特征，尤其是一些局部细节，如“华西雨屏区”的降水高值区能较好地刻画出来。

（2）高分辨率辅助信息的加入有助于在一定程度上维持降尺度结果的精度。在降尺度处理过程中，MGWRK模型综合运用了空间位置、地形等多个影响因素的高分辨率数据，并在此基础上进一步探究了不同因素与TRMM降水间影响关系的空间非平稳性类型与特征，该模型有利于降尺度结果保持原有的精准度水平。从不同年份各评价指标的结果来看，MGWRK法可以使降尺度处理后TRMM降水数据的空间精度与原始数据更为接近，其降尺度效果要优于Bilinear法等传统重采样方法及基于OLS的全局回归克里格法。

（3）经过MGWRK模型降尺度转换后，TRMM降水数据在大幅提升空间分辨率的同时数据精确度仍保持了较好的水平，为TRMM数据在小空间尺度的应用研究奠定基础。本研究构建的降尺度模型适用于四川省TRMM降水数据的降尺度研究。

[1] 张琪,李跃清.近48年西南地区降水量和雨日的气候变化特征[J].高原气象,2014,33(2):372-383.

Zhang Q,Li Y Q.Climatic variation of rainfall and rain day in Southwest China for last 48 years[J].Plateau Meteorology, 2014,33(2):372-383.(in Chinese)

[2] 吴冰洁,王靖,唐建昭,等.华北平原冬小麦产量变异的气象影响因子分析[J].中国农业气象,2018,39(10):623-635.

Wu B J,Wang J,Tang J Z,et al.Meteorological influencing factors on variation in winter wheat yield in the North China Plain[J].Chinese Journal of Agrometeorology,2018,39(10): 623-635.(in Chinese)

[3] Kidd C,Levizzani V,Laviola S.Quantitative precipitation estimation from earth observation satellites[A].Testik F Y,Gebremichael M.Rainfall:state of the science[C].Washington DC:American Geophysical Union,2010:127-158.

[4] 刘元波,傅巧妮,宋平,等.卫星遥感反演降水研究综述[J].地球科学进展,2011,26(11):1162-1172.

Liu Y B,Fu Q N,Song P,et al.Satellite retrieval of precipitation: an overview[J].Advances in Earth Sciences,2011,26(11): 1162-1172.(in Chinese)

[5] 王存光,洪阳.卫星遥感降水的反演、验证与应用综述[J].水利水电技术,2018,49(8):1-9.

Wang C G,Hong Y.Review on inversion,verification and application of satellite remote sensing of precipitation[J]. Water Resources and Hydropower Engineering,2018,49(8):1-9. (in Chinese)

[6] Kummerow C,Barnes W,Kozu T,et al.The Tropical Rainfall Measuring Mission(TRMM) sensor package[J].Journal of Atmospheric and Oceanic Technology,1998,15:809-817.

[7] Iguchi T,Kozu T,Meneghini R,et al.Rain profiling algorithm for the TRMM precipitation radar[J].Advances in Space Research,2000,25(5):973-976.

[8] Karaseva M O,Prakash S,Gairola R M.Validation of high-resolution TRMM-3B43 precipitation product using rain gauge measurements over Kyrgyzstan[J].Theoretical and Applied Climatology,2012,108(1-2):147-157.

[9] 嵇涛,杨华,刘睿,等.TRMM卫星降水数据在川渝地区的适用性分析[J].地理科学进展,2014,33(10):1375-1379.

Ji T,Yang H,Liu R,et al.Applicability analysis of the TRMM precipitation data in the Sichuan-Chongqing region[J].Progress in Geography,2014,33(10):1375-1379.(in Chinese)

[10] 李琼,杨梅学,万国宁,等.TRMM 3B43降水数据在黄河源区的适用性评价[J].冰川冻土,2016,38(3):620-633.

Li Q,Yang M X,Wan G N,et al.Analysis of the accuracy of TRMM 3B43 precipitation data in the Source Region of the Yellow River[J].Journal of Glaciology and Geocryology, 2016,38(3):620-633.(in Chinese)

[11] 陈少丹,张利平,郭梦瑶,等.TRMM卫星降水数据在区域干旱监测中的适用性分析[J].农业工程学报,2018, 34(15): 126-132.

Chen S D,Zhang L P,Guo M Y,et al.Suitability analysis of TRMM satellite precipitation data in regional drought monitoring[J].Transactions of the CSAE,2018,34(15): 126-132.(in Chinese)

[12] Immerzee W W,Rutten M,Droogers P.Spatial downscaling of TRMM precipitation using vegetation response on the Iberian Peninsula[J].Remote Sensing of Environment,2009, 113(2):362-370.

[13] Jia S F,Zhu W B,Lu A F,et al.A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China[J].Remote Sensing of Environment,2011,115(12):3069-3079.

[14] Moon H,Baik J,Hwang S,et al.Spatial downscaling of grid precipitation using support vector machine regression [J].Journal of Korea Water Resources Association,2014, 47(11):1095-1105.

[15] 李净,张晓.TRMM降水数据的空间降尺度方法研究[J].地理科学,2015,35(9):1164-1169.

Li J,Zhang X.Downscaling method of TRMM satellite precipitation data[J].Scientia Geographica Sinica,2015,35(9): 1164-1169.(in Chinese)

[16] 刘小婵,张洪岩,赵建军,等.东北地区TRMM数据降尺度的GWR模型分析[J].地球信息科学学报,2015,17(9): 1054-1062.

Liu X C,Zhang H Y,Zhao J J,et al.Spatial downscaling of TRMM precipitation data based on GWR model in Northeast China[J].Journal of Geo-information Science,2015, 17(9):1054-1062.(in Chinese)

[17] 郑杰,闾利,冯文兰,等.基于TRMM 3B43数据的川西高原月降水量空间降尺度模拟[J].中国农业气象,2016,37(2): 245-254.

Zheng J,Lv L,Feng W L,et al.Spatial downscaling simulation of monthly precipitation based on TRMM 3b43 data in the Western Sichuan Plateau[J].Chinese Journal of Agrometeorology, 2016,37(2):245-254.(in Chinese)

[18] 范雪薇,刘海隆.天山山区TRMM降水数据的空间降尺度研究[J].自然资源学报,2018,33(3):478-488.

Fan X W,Liu H L.Downscaling method of TRMM satellite precipitation data over the Tianshan Mountains[J].Journal of Natural Resources,2018,33(3):478-488.(in Chinese)

[19] 赵娜,焦毅蒙.基于TRMM降水数据的空间降尺度模拟[J].地球信息科学学报,2018,20(10):1388-1395.

Zhao N,Jiao Y M.Downscaling of TRMM satellite precipitation data[J].Journal of Geo-information Science,2018,20(10): 1388-1395.(in Chinese)

[20] Brunsdon C,Fotheringham A S,Charlton M E.Some notes on parametric significance tests for geographically weighted regression[J].Journal of Regional Science,1999,39(3):497-524.

[21] Fotheringham A S,Charlton M E,Brunsdon C.The geography of parameter space:an investigation into spatial non-stationarity [J].International Journal of Geographical Information Systems,1996,10(5):605-627.

[22] Fotheringham A S,Brunsdon C,Charlton M E.Geographically weighted regression:the analysis of spatially varying relationships[M].Chichester:John Wiley & Sons Ltd.,2002: 16-24.

[23] 李豪,刘涛,徐精文.基于混合地理加权回归与克里格的区域降水量空间插值方法[J].中国农业气象,2018,39(10): 674-684.

Li H,Liu T,Xu J W.Spatial interpolation of regional precipitation based on mixed geographical weighted regression combined with kriging interpolation[J].Chinese Journal of Agrometeorology, 2018,39(10):674-684. (in Chinese)

[24] 张润楚.多元统计分析[M].北京:科学出版社,2007:18-40.

Zhang R C.Multivariate statistical analysis[M].Beijing: Science Press,2007:18-40.(in Chinese)

[25] 庄平,高贤明.华西雨屏带及其对我国生物多样性保育的意义[J].生物多样性,2002,10(3):339-344.

Zhuang P,Gao X M.The concept of the Rainy Zone of West China and its significance to the biodiversity conservation in China[J].Biodiversity Science,2002,10(3):339-344.(in Chinese)

[26] 唐永亮.单幅图像超分辨率重建方法研究[D].重庆:重庆大学,2018:2-3.

Tang Y L.Research on single image super-resolution reconstruction method[D].Chongqing:Chongqing University, 2018:2-3.(in Chinese)

Spatial Downscaling of TRMM Precipitation Data in Areas of Complex Terrain: A Case Study in Sichuan Province

LI Hao, LEI Yuan

(College of Resources Science and Technology, Sichuan Agricultural University, Chengdu 611130, China)

Precipitation data have became an indispensable part for agriculture, hydrological, meteorological, ecological and other environmental applications. Satellites obtain the earth's precipitation data from space through on-board sensors, which is playing a more and more important role in the data collection currently. Research increasingly suggests that satellite-derived precipitation products with their advantages in the continuity of spatial scale and high degree of prediction accuracy have vast space for development. It is well-known that use of the Tropical Rainfall Measuring Mission (TRMM) has been widely employed for obtaining global precipitation data recently due to its incomparable superiority to traditional method. However, the application is subject to certain restrictions by the relatively low spatial resolution (about 20−30km) of the data. Considering various influence factors such as spatial location and terrain and their spatial non-stationary characteristics, a case study on the application of mixed geographic weighted regression combined with Kriging interpolation (MGWRK) for spatial downscaling of the TRMM annual precipitation data was undertaken at Sichuan Province, Southwest China with a significant space differentiation of precipitation. And in the meantime, assessment of the downscaling results derived by different methods were carried out based on the measured data of 41 meteorological stations. Some results in this study showed that: (1) by use of the MGWRK model for downscaling, the spatial resolution of TRMM precipitation data was increased sharply from 0.25° (about 26km) to 1km, which can describe the spatial variation of precipitation more detailly and effectively in study area. (2) The MGWRK model not only attempted to use a combination of various auxiliary information with high-resolution such as spatial location and terrain, but also explored the characteristics of spatial stationary of the relationship between TRMM precipitation and its factors. From the assessment results of various downscaling approach to the TRMM data of mean annual values (1998−2017) and the two typical years’ values (the wet year at 1998 and the dry year at 2006), it was found that the MGWRK method can prove a higher accuracy compared with the OLS-based global regression Kriging (GRK) and the Bilinear resample (Bil) method and obtain a result that is more approximate to the original status. (3) The downscaling model presented in this paper considered the improvement of spatial resolution without compromising the maintaining accuracy and therefore it is obviously an approach available for the spatial downscaling of TRMM precipitation data in study area and contribute to define a foundation for the application of the TRMM data in small scale.

TRMM precipitation data; Spatial downscaling; Mix geographically weighted regression; Sichuan Province

10.3969/j.issn.1000-6362.2019.10.001

李豪,雷苑.复杂地形下TRMM降水数据的降尺度研究:以四川省为例[J].中国农业气象,2019,40(10):607-619

2019−02−20

国家自然科学基金项目（41501291）

李豪（1980−），博士，讲师，主要从事3S技术在水土资源可持续利用方面研究。E-mail：lihao@sicau.edu.cn