超宽斜拉桥双边箱主梁恒载剪力滞效应研究
2019-10-18成立涛李文华
孙 宁,成立涛,李文华
(中交第一公路勘察设计研究院有限公司,陕西 西安 710075)
0 引 言
近年来,随着国民经济和城市建设的快速发展,人流量和车流量迅速增大。为了容纳更大的与现代生活特征相适应的机动车流、非机动车流和人流,出现了城市宽桥以及宽跨比较大的斜拉桥,如:福州三县洲闽江大桥(238 m+179 m独塔单索面预应力混凝土斜拉桥),桥宽30 m,宽跨比12.6%;泉州晋江大桥(200 m+165 m独塔双索面预应力混凝土斜拉桥),桥宽38 m,宽跨比19%;福州浦上大桥(72 m+110 m+110 m+72 m三塔矮塔单索斜拉桥),桥宽37.5 m,宽跨比34%[1]。双边箱主梁截面结构因其质量轻、施工方便等优点,正越来越多地出现在斜拉桥主梁设计中[2]。同时,随着主梁宽度的加大,宽跨比增大,其截面剪力滞效应越来越明显,如果忽略其影响,结构设计将偏于不安全。而采用单梁模型将无法准确考虑结构的空间受力特性,故需采用空间实体模型进行分析,了解主梁剪力滞规律,指导结构设计。
本文以某大跨度超宽斜拉桥为研究背景,采用ANSYS有限元分析软件建立空间实体模型,对其进行空间受力状态和剪力滞效应分析,以期为其他同类型结构设计提供参考。
1 工程概况
该斜拉桥结构体系为(120+120)m独塔双索面预应力混凝土斜拉桥,整幅桥面宽59.5 m,索塔为天鹅造型,两侧各有17根拉索,如图1所示。
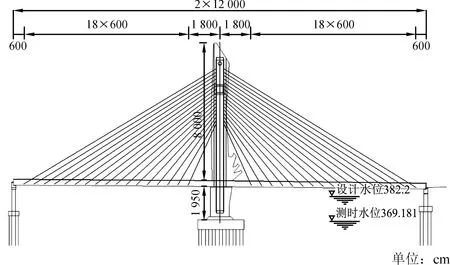
图1 斜拉桥立面
本桥主梁采用边箱梁开口截面,箱梁底面为平坡,箱梁中心处梁高3.5 m,顶面为1.5%双向横坡,拉索锚固位置的纵梁宽3 m,两侧边腹板厚度40 cm,标准段箱梁顶板厚30 cm,底板厚40 cm;在主塔附近,顶板加厚至60 cm,底板加厚至80 cm。箱梁顶面全宽59.5 m,悬臂采用2.5 m,边腹板内倾5 m,底板全宽44.5 m,边腹板与顶、底板采用半径6 m的圆弧倒角进行过渡。为改善桥面板的受力,主梁纵向在顶板下缘设置了3道宽30 cm、高70 cm的加劲肋,加劲纵梁与桥面板相交处设置20 cm×20 cm的倒角,如图2所示。
主梁纵梁在主塔位置设置了740 cm×490 cm的开口,以便主塔竖向通过,纵梁从标准段3 m宽过渡到主塔附近8.2 m宽。
一段主梁标准节段长6 m,节段处设横隔板,横隔板厚40 cm;主塔附近采用100 cm及45 cm横隔板;端横梁厚188 cm,全桥横梁均采用预应力混凝土结构。主梁分为2×(10 m+5×18 m)+40 m共13个施工节段,主梁采用支架现浇。

图2 箱梁断面构造
主梁内配置的纵向钢束分顶板束、底板束及腹板束,均为通常束。为减少不同箱梁前后浇筑引起的横向收缩裂缝,横向顶板内配置了预应力钢束。
2 基本结构选定及建模
本研究主要关注在结构自重、二期铺装、斜拉索索力及预应力作用下的主梁剪力滞效应。在忽略纵坡的情况下,由于荷载和结构基于主塔横轴、纵轴对称,为减小模型规模,计算取全桥的1/4模型,如图3所示。为尽可能真实地反映结构的空间应力分布,建模时对主梁的构造细节进行模拟,小纵梁、各类横梁、塔梁接触段、跨中渐变段都按设计进行空间建模(图4)。为准确模拟边界,同时对主塔、斜拉索进行空间建模。结构分析表明,对于超宽斜拉桥结构,横向横梁预应力钢束的布置也将影响其纵向应力分布。故按设计要求,模型中考虑纵、横向预应力作用。
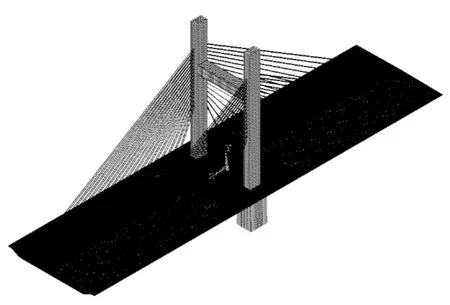
图3 全桥1/4有限元模型扩展

图4 标准梁段1/2模型单元离散
在有限元模型中,采用SOLID45单元模拟混凝土主梁,采用BEAM189单元模拟主塔,采用LINK10单元模拟斜拉索及预应力钢筋,采用COMBIN14单元模拟支座。因采用梁单元模拟主塔,故采用MPC184刚性连接单元模拟其与支座的连接。
为考虑预应力效应,预应力钢筋按其空间位置采用LINK10单元建模,采用约束方程法实现预应力钢筋单元与主梁混凝土单元的连接,并采用APDL技术编程计算预应力损失,按钢束单元有效应力计算初应变,设置LINK10单元的初应变。
边界条件为:塔根固结,不考虑桩土效应;采用支座实际刚度,并通过COMBIN14单元模拟,支座下节点固结;对称处采用对称约束。
3 模型验证
为验证模型的正确性,利用ANSYS面操作技术取主梁横截面正应力对其质心的矩,得到截面弯矩,与MIDAS Civil中的单梁模型弯矩计算结果进行比较,两者基本吻合,精度满足工程要求,结果见图5,图中弯矩以主梁下部受拉为正。主梁在恒载作用下的弯矩呈波浪形,由于拉索的弹性支承作用,斜拉桥主梁的弯矩显著减小[3]。这说明该桥恒载分布、主梁刚度及拉索索力是满足工程要求的。
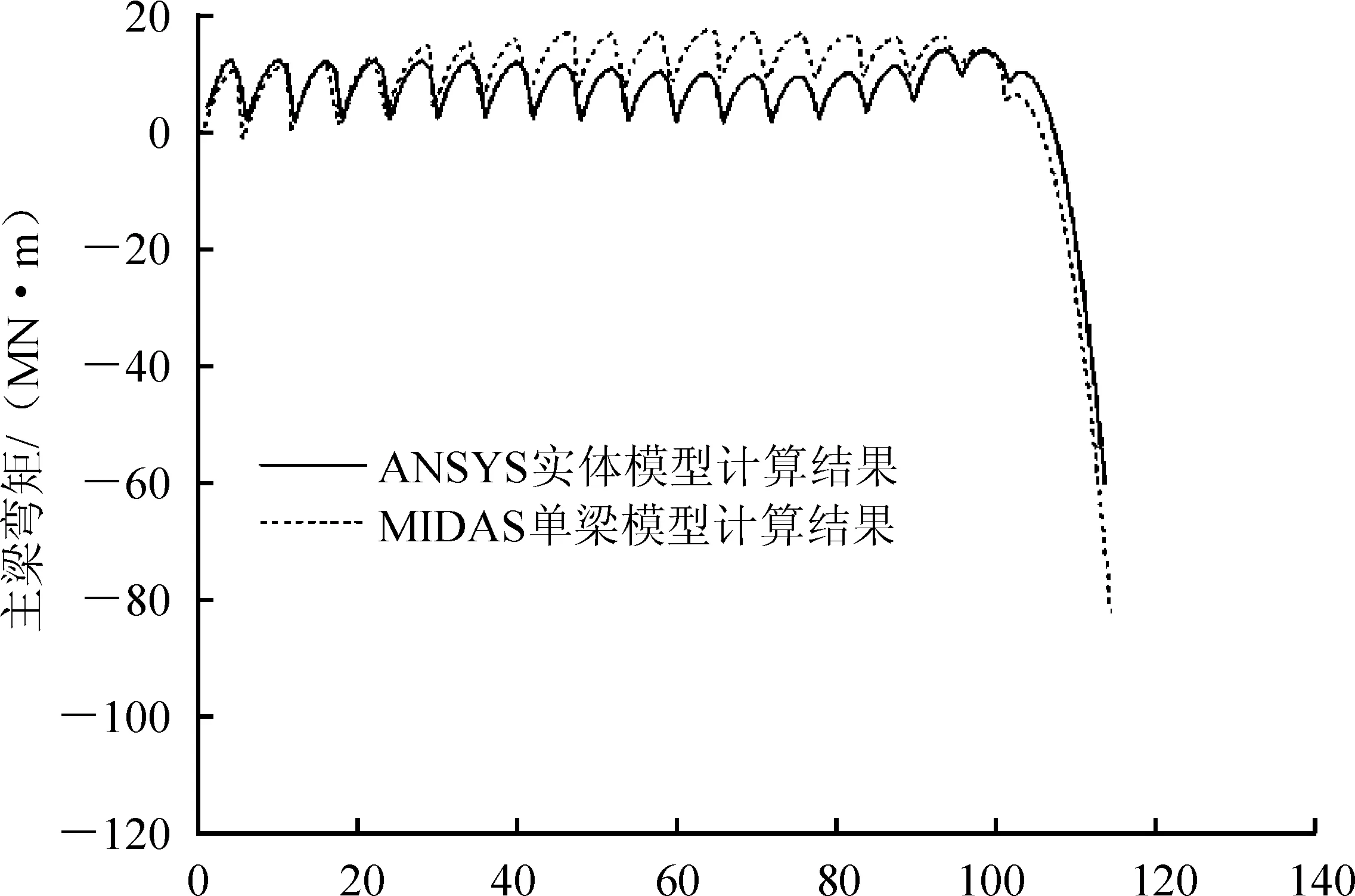
图5 实体模型计算弯矩与单梁模型的比较
4 剪力滞效应分析
4.1 剪力滞计算方法及梁段各点剪力滞系数
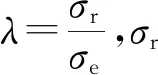

图6 主梁横截面各点示意
计算恒载作用下的主梁上缘、下缘各点的正应力及其剪力滞系数。主梁上缘B~G点沿纵桥向的剪力滞系数变化见图7;主梁下缘H~L点的沿纵桥向的剪力滞系数变化见图8。从图7、8可以看出,超宽斜拉桥主梁沿纵向各截面剪力滞效应不同:边墩等截面约束较弱处,其截面各点处剪力滞效应明显;中间标准梁段处,剪力滞效应具有明显的周期性。图9、10分别为上、下缘各点正应力值。

图7 上缘各点剪力滞系数沿纵桥向的变化
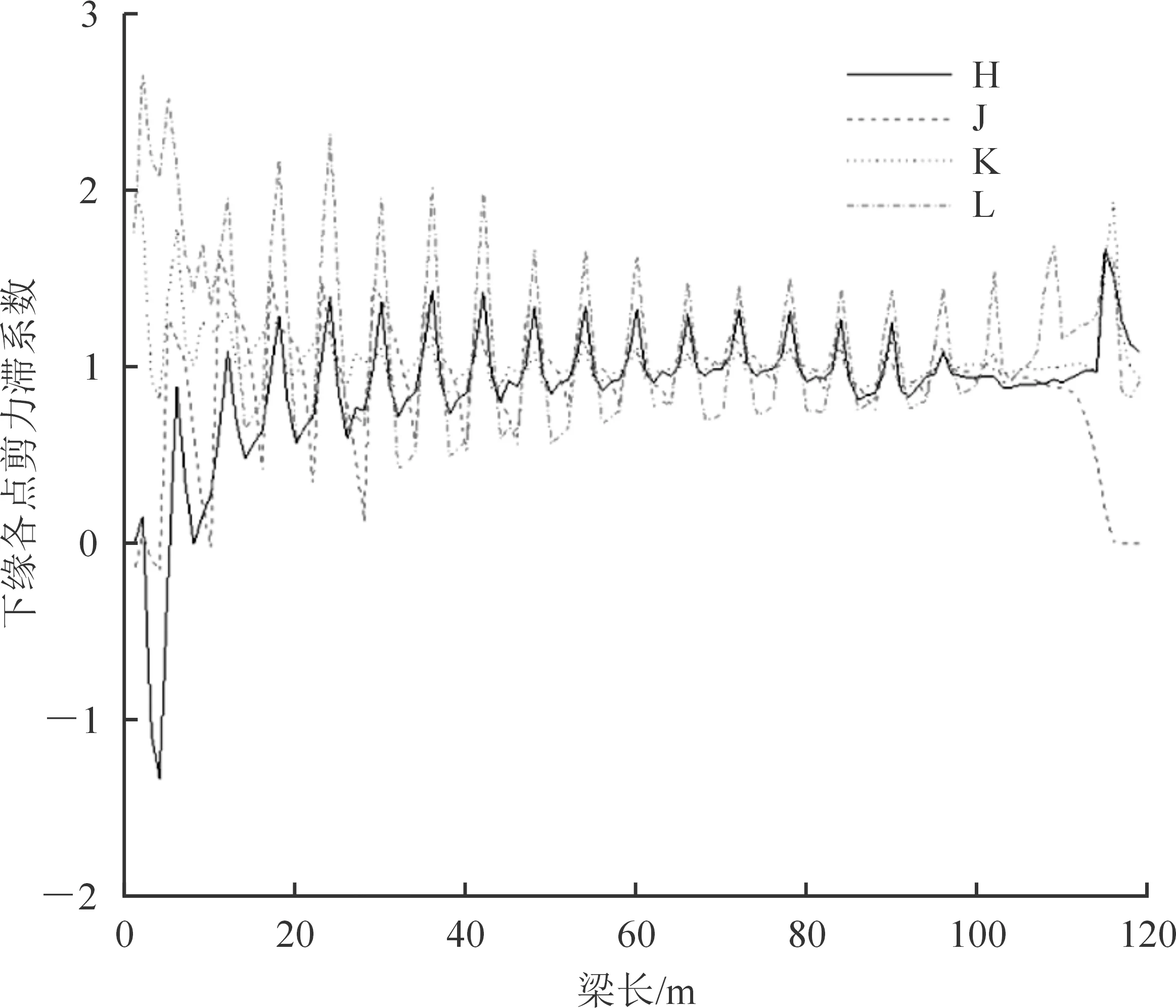
图8 下缘各点剪力滞系数沿纵桥向的变化
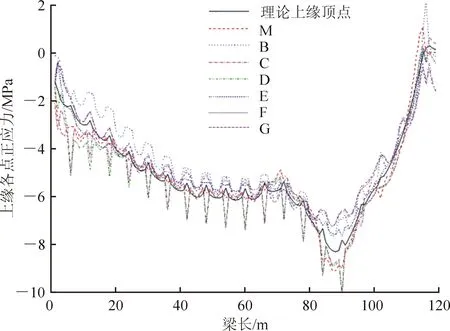
图9 上缘各点正应力
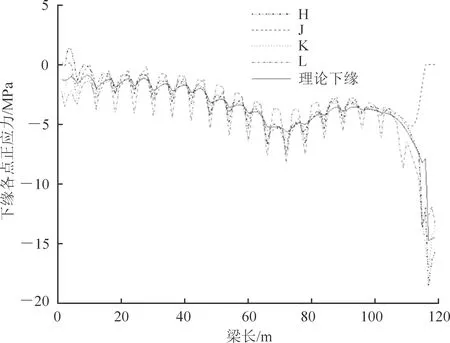
图10 下缘各点正应力
整体上看,在主梁靠近主塔的负弯矩区段及边墩区段,剪力滞系数变化较大,其余梁段剪力滞系数在1.0附近上下摆动。
4.2 标准梁段剪力滞分析
各标准梁段剪力滞变化规律类似:沿纵向2个索力作用点之间的箱梁剪力滞效应具有明显的周期性,沿横向索力作用点附近,箱梁剪力滞效应变化最大,远离索力作用点剪力滞效应变化趋缓。
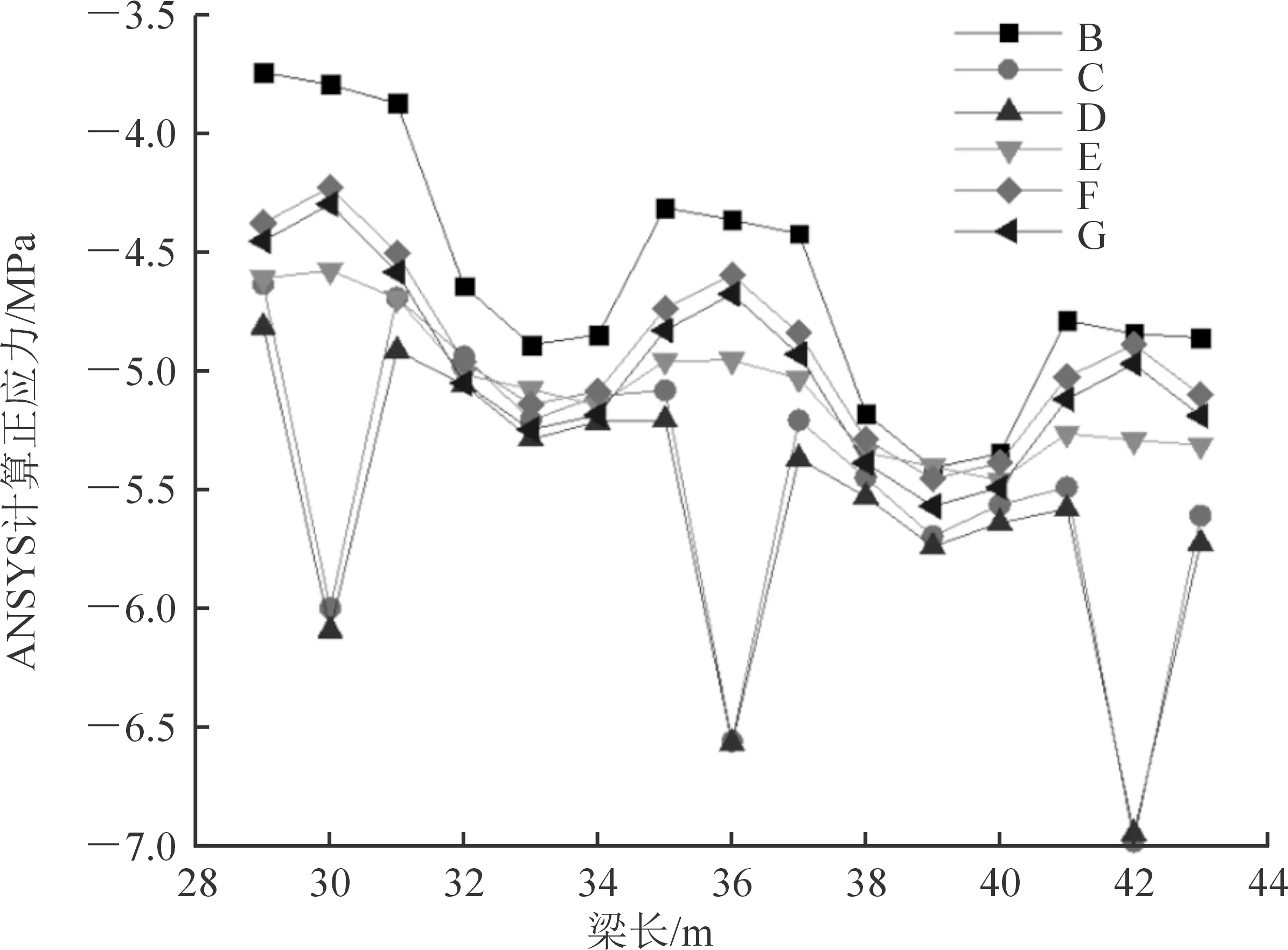
图11 29~43 m梁段的上缘各点计算正应力(以拉力为正)
为分析其变化规律及原因,考虑距边墩29~43 m梁段的ANSYS计算正应力,见图11。从图中可以看出:B、E、F、G点变化规律相似,在一个梁段2根吊索位置之间,压应力具有先增大后减小的趋势;C、D点变化规律相似,在一个梁段2根吊索位置之间,压应力变化规律可分为2个阶段。阶段一:压应力先突增后减小,形成应力尖点;阶段二:压应力先缓慢增大至极值后减小。另外可以看出,C、D点压应力最大,其次是E、G、F点,B点最小。
C、D两点位于主梁实体段两侧,是轴力传递的主要途径。拉索对主梁施加轴力和弯矩(吊点作用于截面质心下缘,故产生弯矩效应)后,轴力首先影响C、D两点的正应力,使其迅速增大,而后轴力通过横梁迅速扩散,此时C、D两点正应力下降。由于2根吊索之间的梁段在重力作用下受正弯矩作用,上缘受压,且跨中弯矩最大,故C、D点正应力跨中出现极值;靠近右侧拉索时,受到右侧拉索的拉力作用,正应力相应减小。同样在拉索右侧,B点受轴力影响,正应力相应增大,在跨中弯矩作用下出现压应力极值。B、E、F、G点由于离轴力传递区域较远,没有出现类似C、D点的应力突变,受弯矩作用影响明显。
标准梁段计算所得的剪力滞效应最大出现在C、D点,标准段(距边墩16~80 m)C点最大剪力滞系数为1.375, D点最大值为1.49。斜拉索索力作用点附近剪力滞明显,纵向索力作用点间剪力滞效应趋缓。标准段沿纵向两个索力作用点之间的箱梁剪力滞效应具有明显的周期性,沿横向索力作用点附近,箱梁剪力滞效应变化最大,远离索力作用点剪力滞效应变化趋缓。
4.3 主塔及边墩附近的剪力滞分析
靠近主塔处,主梁弯矩为负弯矩(图12),此时G点压应力最大,其次是F、E、D、C等点,原因在于主梁弯矩和轴力主要由主梁实体段传递,故C、D、M点的应力与理论计算结果接近,而G、F、E点存在剪力滞效应,仍承受较大压应力。由于该梁段处理论应力数值较小,因此剪力滞系数比一般梁段大。主梁负弯矩区段(107~120 m)C、D点为正剪力滞效应,上翼缘其余各点均为负剪力滞效应。边墩附近主梁受正弯矩,上缘受压(图13),而G、F、B点压应力小,说明其剪力滞明显。

图12 主塔附近梁段上缘各点正应力比较
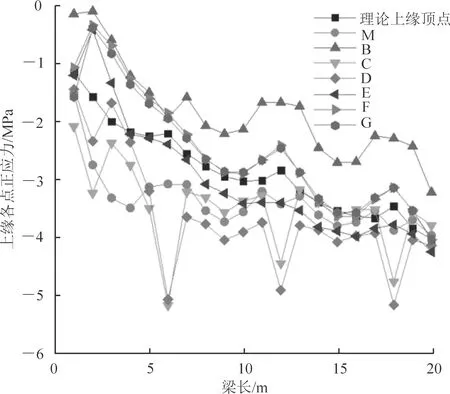
图13 边墩附近上缘各点正应力分布
5 结 语
通过分析该超宽斜拉桥在双边箱主梁自重、二期恒载及预应力作用下的剪力滞,得到以下结论。
(1)超宽斜拉桥双边箱梁属于受弯矩和轴力共同作用的构件,在研究剪力滞效应时,需考虑轴力的影响,而且从标准段剪力滞效应的分析中可见,轴力的影响不可忽略。
(2)超宽斜拉桥主梁剪力滞效应明显,设计类似桥梁时,需采用空间模型进行分析,或根据其剪力滞效应系数增加主梁压应力储备。
(3)超宽斜拉桥主梁沿纵向各截面剪力滞效应不同,在边墩等截面约束较弱处,其截面各点处剪力滞效应明显,但应力绝对值往往较小,具体设计时可选取较大剪力滞系数来校核,防止局部拉应力超限。
(4)主梁标准段在两横梁间剪力滞效应具有明显的规律性,可利用该规律性研究剪力滞效应的简化计算方法。
