护栏对空心板梁桥校验系数的影响分析
2019-10-18程咏春
程咏春
(中交路桥建设有限公司,北京 101107)
0 引 言
防护栏是公路桥梁上最基本的安全设施,大量的荷载试验结果表明,防护栏对提高主梁结构的承载能力有一定的贡献[1]。
在进行板桥设计时,一般将护栏作为二期恒载施加在主梁上,不考虑护栏对桥梁结构承载能力的贡献;而现在修建的护栏一般与桥梁结构刚接在一起,其钢筋配置越来越多,高度越来越大,如不考虑护栏对桥梁结构的影响,计算结果将与桥梁结构的实际受力状态不相符。实践证明,护栏提供的刚度并非是平均分配给每一片板,而是沿桥梁结构横向合理分布在有限宽度范围内。因此,许多学者对此做了大量研究。文献[2]中护栏刚度沿桥梁结构横向呈三角形分布在14%的桥面宽度,由于桥面宽度的限制,桥梁越窄,护栏提供的刚度影响越明显,因此该分布模式具有一定的局限性。邹兰林[3]提出护栏刚度沿桥梁横向呈三角形分布在两块边板上,该分布模式计算简便,但是与实际分布状态有一定的偏差。由于获得实际桥梁样本不容易,因此护栏对结构受力程度的影响如何还有待于进一步研究。本文以1座无护栏空心板桥和1座有护栏空心板桥的荷载试验为依托,通过实测挠度校验系数分析,提出护栏提供的刚度沿桥梁横向的合理分布形式,并通过应变校验系数及频率得以验证,为有护栏的桥梁荷载的校验系数提供理论依据。
1 理论分析
计算假定如下。
(1)同一座桥各片主梁的校验系数是一定的。
(2)材料特性和施工条件相同的2座桥校验系数应相等。
根据校验系数相等的原则,可由无护栏桥的校验系数推出有护栏桥的理论挠度值,根据挠曲线方程EIy″=M列出挠曲线近似微分方程,进而积分变换得出各片板的惯性矩I,分别如式(1)、(2)。
式中:y为竖向荷载作用下的挠度值;x为沿梁纵向的任意一点坐标;a、b为外力FP距左右两端支座的距离;l为结构跨径;E为主梁的弹性模量;I为主梁的抗弯惯性矩。
求出有护栏桥的抗弯惯性矩与无护栏桥各片板的惯性矩差值,即可近似认为是由护栏等效到各片板上的惯性矩。先假设把护栏等效成矩形,其宽度为空心板宽,即可计算出护栏的等效高度h。考虑护栏刚度应在有限宽度范围内渐变分布,将等效矩形拟合成连续线型,即可确定护栏刚度沿桥横向的分布形式。
2 依托工程概况
A中桥和B中桥均是国道219线新藏公路(西藏境)区界至日土段改建整治工程的简支空心板桥,两桥梁设计单位、施工单位均相同,其中A中桥无护栏,B中桥有护栏。2座桥的基本概况如表1所示。
对2座桥进行荷载试验,选择跨中位置作为试验控制截面,其荷载试验[4]分为中载和偏载2个工况,横向布置2辆车,各工况计算加载效率均为1.03,加载车采用2辆36.83 t三轴车(车重和货重),车辆平均两后轴合计重29.49 t,前轴重7.34 t。
每片空心板底中部各布置1个应变测点和1个挠度测点,各工况加载位置和测点布设如图1所示(以B中桥的横断面示意,A中桥的加载位置和测点布设相同),图中梁号与应变测点、挠度测点编号均相同。B中桥和A中桥的实测挠度值和实测应变值见表2、3。
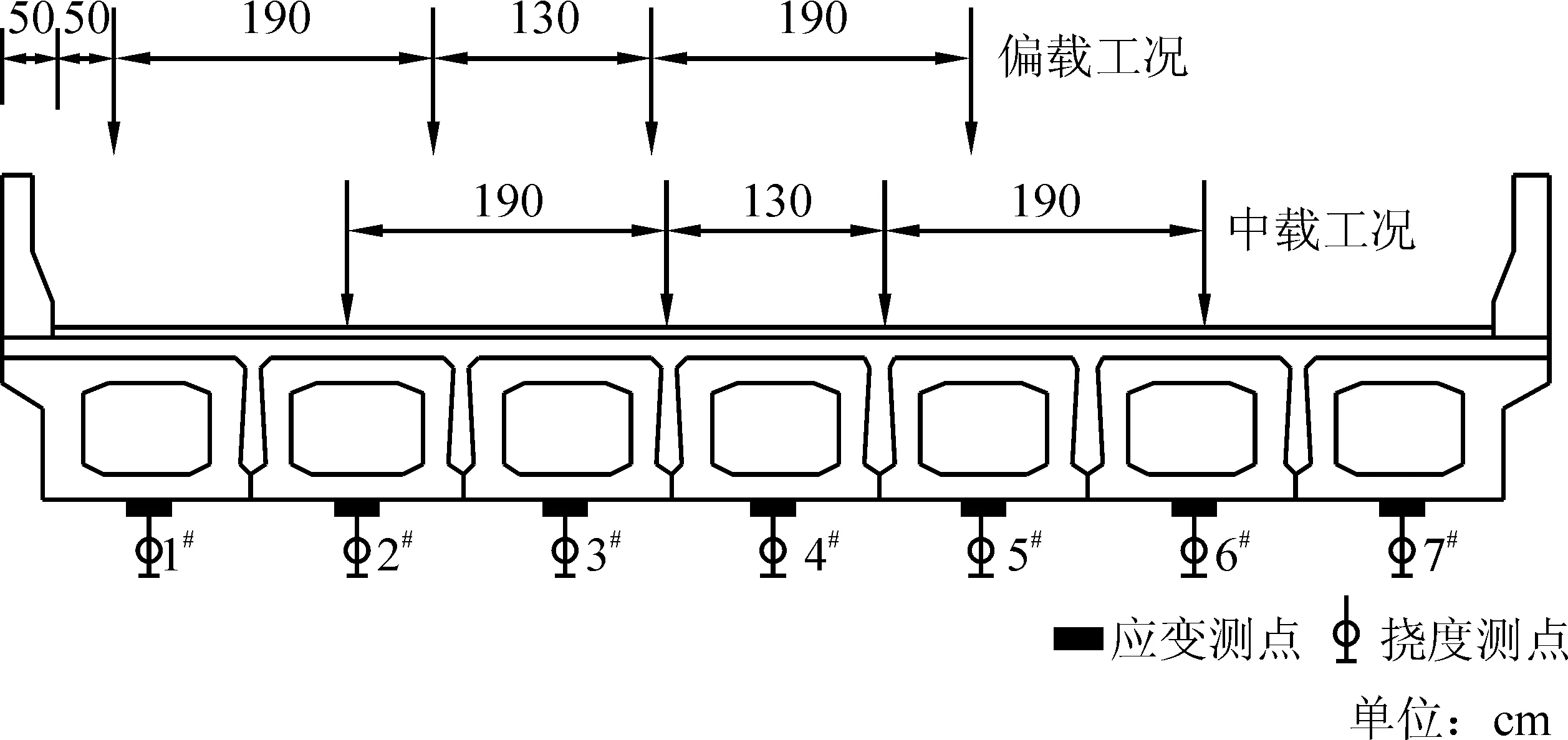
图1 B中桥加载布置及测点编号
利用桥梁空间分析模型Midas Civil-2013进行梁格法[5]建模。其中,A中桥共建立182个梁单元,B中桥共建立198个梁单元,梁的一端约束x(纵向)、y(横向)、z(竖向)方向的位移和x、z方向的转动,另一端约束y、z方向的位移和x、z方向的转动。横向虚拟横梁[6]采用释放梁端约束,刚度取值以与铰接板法计算出单梁的弯矩和挠度相等为原则,试算出虚拟横梁的刚度。结构离散图如图2、3所示。
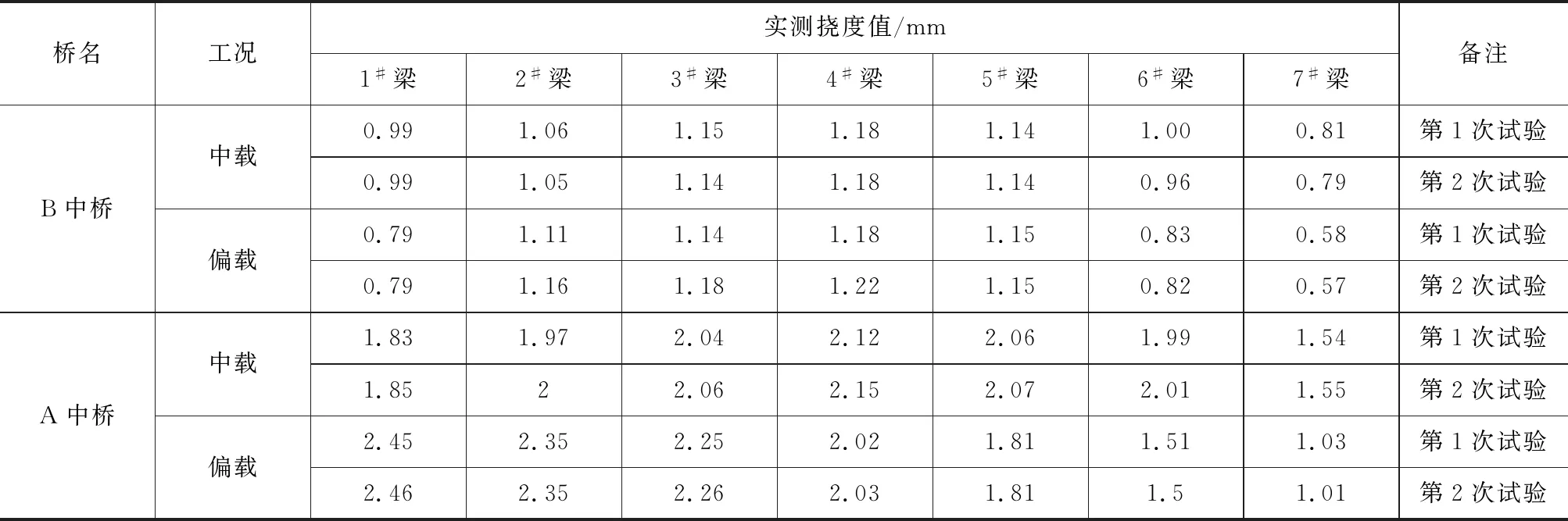
表2 试验实测挠度值
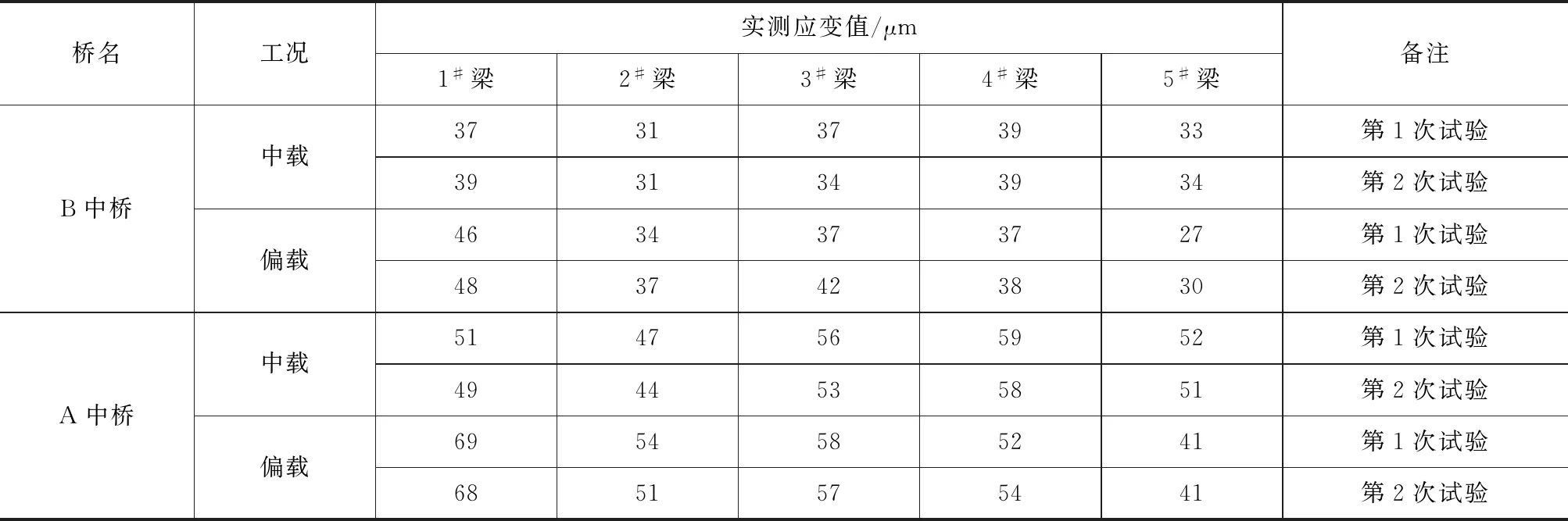
表3 试验实测应变值
注:6#、7#梁应变值测量值误差较大,故未列出。
图2 A中桥结构离散图
图3 B中桥结构离散图
3 实桥挠度校验系数对比
通过荷载试验在2种工况下测得2座桥的挠度实测值对比,如图4所示。
由图4可得:B中桥(有护栏)的挠度值明显减小,尤其是靠近护栏的边板测点值偏小。这说明护栏可以提供一定的刚度,对结构承载能力是有一定贡献的,计算时应考虑护栏参与主梁受力的影响。
在不考虑B中桥护栏作用的条件下,计算出B中桥和A中桥的挠度校验系数[7],见表4。
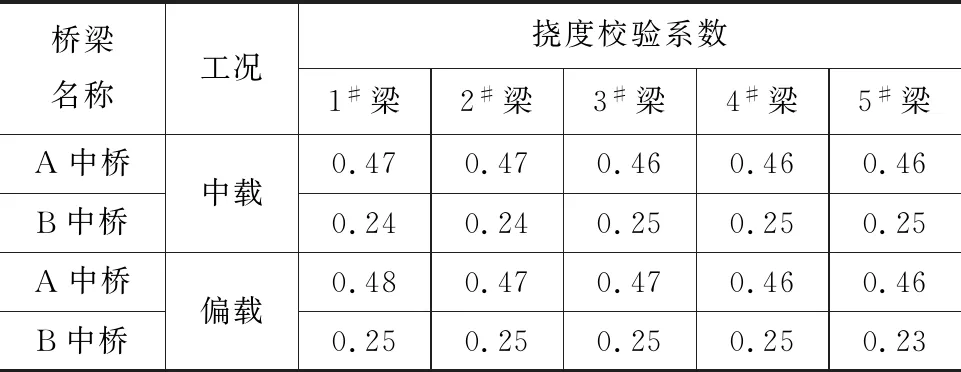
表4 挠度校验系数对比
由表4可知:在不考虑护栏的条件下,2座桥的校验系数相差较大,由此可推断校验系数差值应是由护栏提供的刚度[8-9]抵消。
4 护栏刚度沿桥梁横向分布的特点
分别提出以下3种护栏的刚度分布模式:模式1为三角形分布在2块板上;在模式1基础上,以三角形在板边的点为控制点,拟合出模式2,即曲线分布在2块板上,其趋势类似于T梁受压翼缘实际压应力分布的形式;模式3为三角形分布在3块板上,如图5所示。
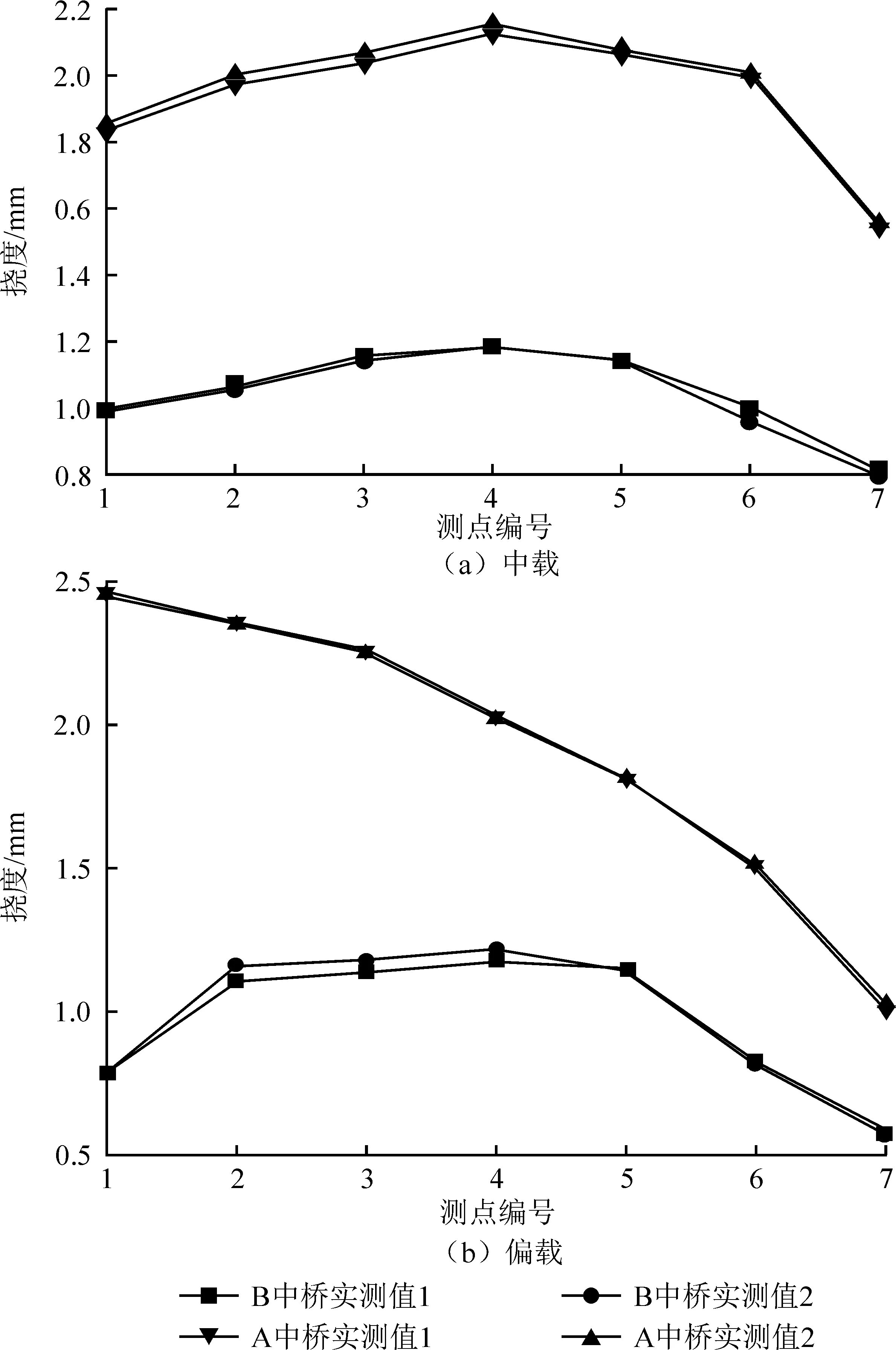
图4 实测挠度对比
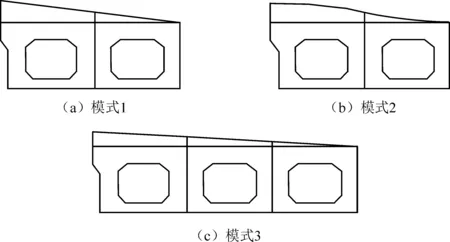
图5 护栏刚度分布模式
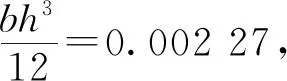
通过表5及图6可以看出,在中载及偏载作用下,3种受力模式考虑护栏参与主梁受力所计算的测点挠度校验系数与无护栏的测点挠度校验系数非常接近,其偏差对比分析见表6。
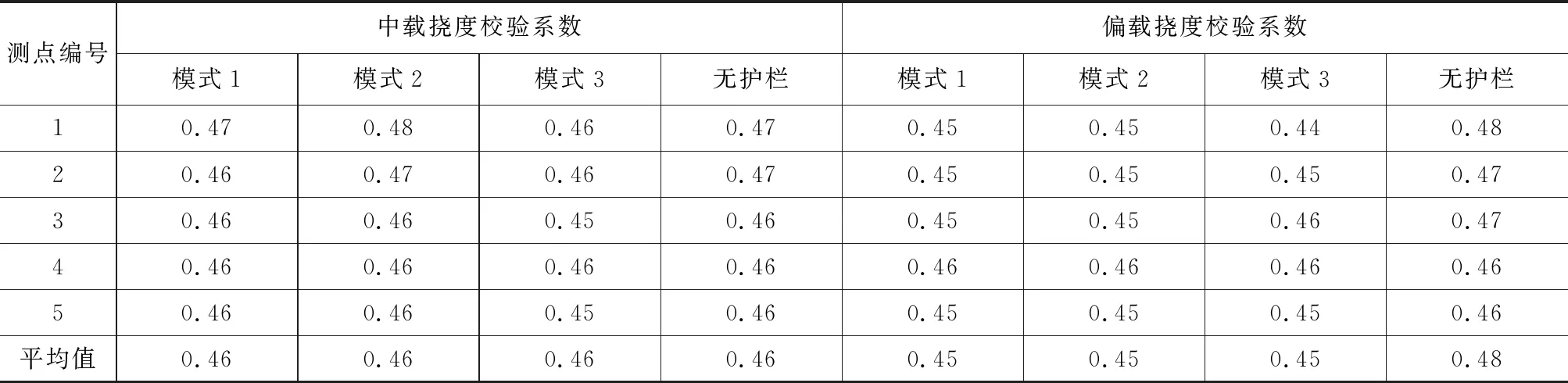
表5 挠度校验系数对比
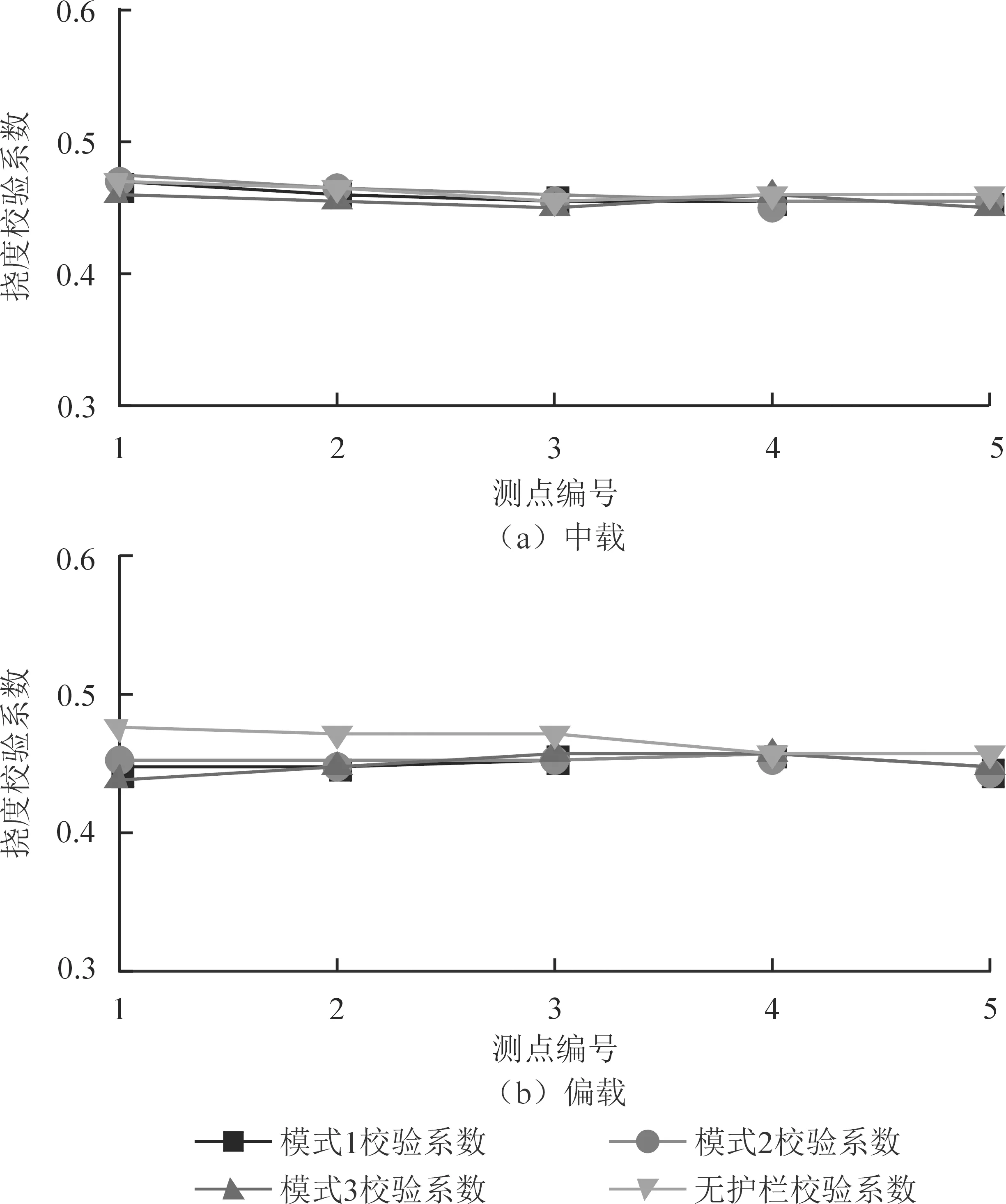
图6 挠度校验系数对比
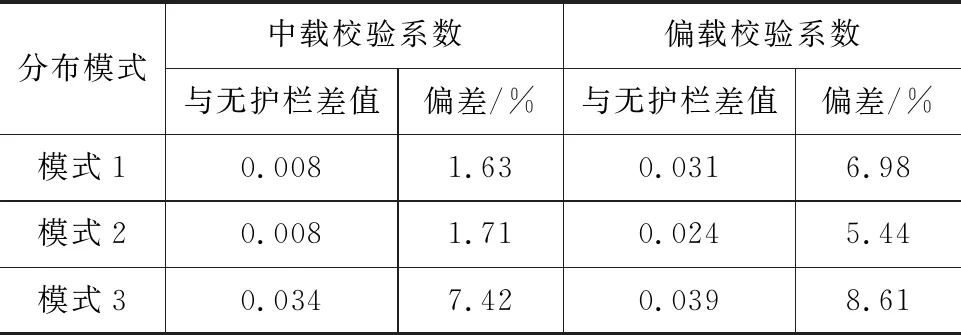
表6 挠度校验系数偏差对比
经对比分析可知,模式2的校验系数与无护栏的校验系数更为接近。
5 护栏刚度对荷载横向分布的影响
荷载横向分布系数[10-11]可根据测试截面各主梁的测点挠度按式(3)进行计算。
(3)
护栏刚度3种分布模式的实测的荷载横向分布系数对比见图7。

图7 荷载横向分布系数对比
由图7可知:3种模式计算出的B中桥的荷载横向分布系数与由实测值计算出的荷载横向分布系数很接近。其偏差对比分析见表7。
对比分析得出,模式2的中载荷载横向分布系数与实测值的荷载横向分布系数更为接近[12-14]。
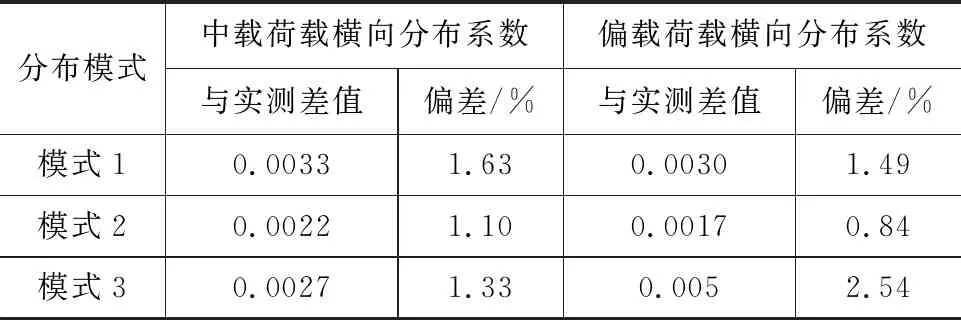
表7 荷载横向分布系数偏差对比
6 护栏刚度横向分布模式的验证
6.1 基于应变校验系数的验证
按照护栏刚度3种分布模式计算出B中桥(有护栏)的应变校验系数,与A中桥(无护栏)的应变校验系数对比,如图8所示。
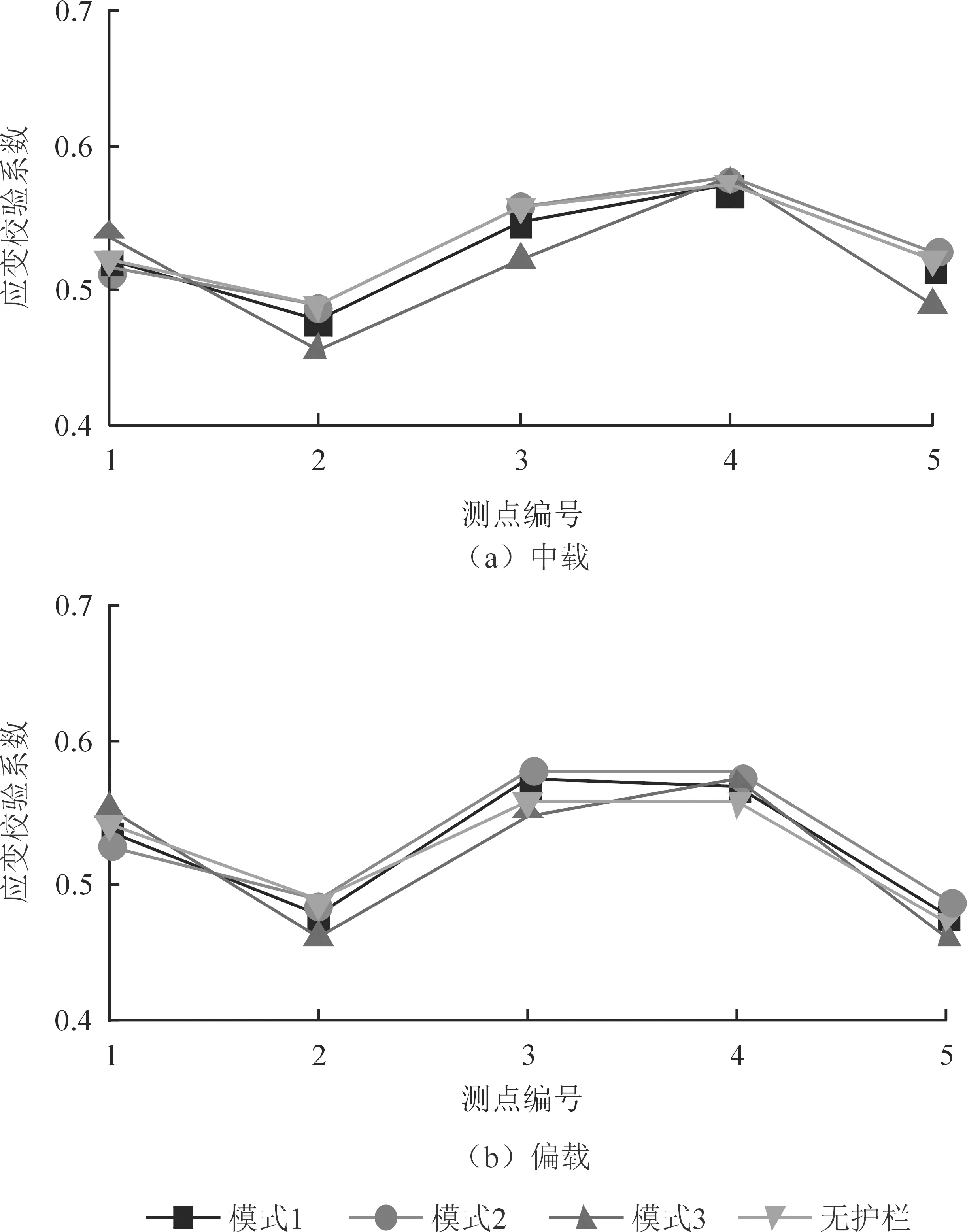
图8 应变校验系数对比
由图8应变校验系数对比可以得出:模式1和模式2计算出的B中桥(有护栏)的应变校验系数与A中桥(无护栏)的应变校验系数更为接近,其偏差对比分析见表8。
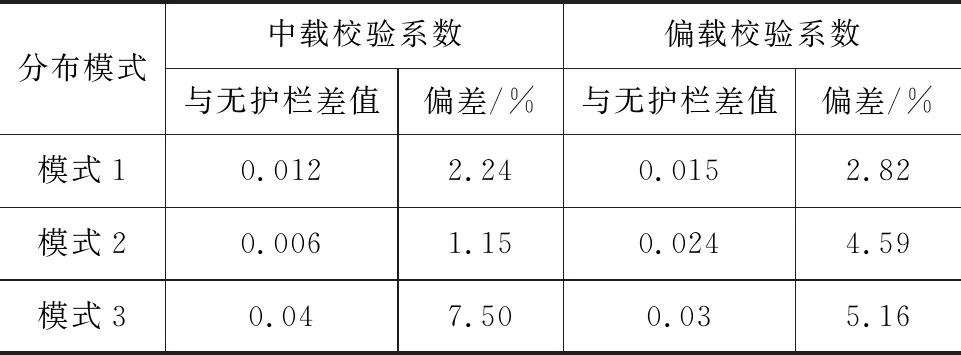
表8 应变校验系数偏差对比
对比分析得出,模式2的中载校验系数与无护栏校验系数更为接近,模式1的偏载校验系数与无护栏校验系数更为接近。
6.2 基于基频的验证
由Midas-civil 2013建模计算出护栏刚度分布模式的基频理论值见表9。
经理论计算基频与实测值对比,模式2的基频更接近于实测值,而模式1与模式2的理论计算基频相差较小。
7 结 语
(1)由2座板桥的荷载试验挠度实测值对比分析可知,护栏参与了主梁受力;由此提出了护栏等效到各片空心板上的惯性矩分析方法,在此基础上给出了护栏的等效高度计算方法。
(2)提出了护栏刚度沿横桥向分布的3种模式,实桥荷载试验的挠度计算对比分析表明,护栏刚度沿桥梁横向呈曲线分布到2块边板上与实际受力状态更为接近,并由同样条件下的应变试验值以及实测基频得到验证。
(3)模式1(护栏刚度以三角形横向分布于2块边板上)与模式2(刚度以曲线形式分布在两块边板上)的计算结果较为接近,但前者计算相对简便,故空心板荷载试验效应理论值计算时可以选取模式1来考虑护栏参与主梁的受力情况。
