黄柏河流域近40年极端降水变化特性分析

黄珂珂 董晓华 陈 亮 张 清 严东英

(1.三峡大学 水利与环境学院,湖北 宜昌 443002;2.水资源安全保障湖北省协同创新中心,武汉 430072)

极端降水事件与洪涝灾害密切相关[1],其引发的灾害给工农业生产、人民生活、自然生态造成巨大的损失[2-5].系统地研究极端降水事件的时空演变特征对减少极端降水事件的危害有非常重要的意义.近年来,越来越多的专家学者开始关注极端降水事件.孙军[6]等人利用中国2 000多个站点50年以上的日降水资料提取6个极端降水指数,结果表明极端降水与年总降水趋势不完全一致,但与夏季总降水有更加一致的趋势性;毕宝贵[7]等人将2016年的强对流和极端降水天气特征与1981年以来的同期天气对比分析,发现超强厄尔尼诺事件结束当年,极端降水和强对流天气发生频次明显较多;时光训[8]等人利用长江流域131个气象站数据,分析了长江流域极端降水的时空变化特征,结果表明长江流域主要强降水指数变化呈增加趋势,降水过程不稳定,容易发生洪涝灾害;潘欣[9]等人采用长江流域内1960～2010年逐日降水资料,分析了长江流域极端降水特性,结果表明未来极端降水将继续以上升趋势为主,流域洪涝灾害风险加大.周兰庭[10]等人采用了云物元模型对极端降雨事件增多地区的土石坝进行安全评价.

宜昌市河网密集、水量丰富,多年平均降水量1 220 mm,4～9月降水量占全年降水总量的70%～80%,洪涝灾害频发[11-12].黄柏河是宜昌市重要的水源地[13],为夷陵区等共7个县市区200万人口及100万亩农田供水.因此,分析黄柏河流域的极端降水事件变化规律对宜昌市的可持续发展意义重大.本文利用极端降水指数对黄柏河流域的极端降水事件进行研究,有助于初步把握黄柏河流域的降水变化特征,全面分析黄柏河流域极端降水事件变化规律和趋势,为预防黄柏河流域的洪涝灾害,保障宜昌市用水安全,加强黄柏河流域水资源的可持续发展提供依据.

1 研究区域概况

黄柏河位于宜昌市城区西北部、长江三峡南津关下游北岸,全长162 km,流域面积1 902 km2(如图1所示),是长江的一级支流,分东、西两条支流,在夷陵区黄花乡两河口汇合,于葛洲坝枢纽三江船闸上游引航道汇入长江.黄柏河流域东支上有尚家河、天福庙、西北口、玄庙观4座水库,总库容约3.2亿m3,经过几十年的开发建设,形成了以防洪、供水、发电为主的水资源调配工程体系.

图1 研究区流域概况

2 数据与研究方法

2.1 数据

本文基于黄柏河流域上游的天福庙水库雨量站和下游的尚家河水库雨量站1978～2016年逐日降水数据,分析该流域极端降水指数序列的趋势性和突变性.世界气象组织气候学委员会成立的气候变化检测指数专家组(ETCCDMI)为了定量研究极端气候事件,提出了27个极端气候指数,在极端气候变化研究中得到广泛应用[14-16].本文选取了其中几个与极端降水相关的指数进行分析,包括大雨日数、年降水强度、异常降水总量、连续无雨日数、连续降水日数、年降水量.这些指数用于表征研究区的极端降水的强度、持续时间及降水量等方面的变化.本文基于这些极端降水指数(见表1),分析黄柏河流域极端降水事件的变化特性.

表1 极端降水指数

为分析极端降水指数在空间上的分布特征,计算 两雨量站极端降水指数多年平均值(见表2).除年降水量(PRCPTOT)相差较大(相差20 mm左右),其他极端降水指数多年平均值均相差不大.

表2 极端降水指数多年平均值

2.2 研究方法

由于目前对于极端降水突变现象的物理机制尚不明确,不同检验方法可能会导致不同的结果,本文采用多种方法对极端降水指数进行突变和趋势性分析,研究黄柏河流域极端降水事件的变化特性.

利用滑动平均法[17]和Sen's法[18-19]对极端降水指数进行趋势性分析,Kendall秩次相关检验[17]进行趋势检验,取显著性水平为0.05.滑动平均法可以消除周期变动和随机波动对时间序列的影响,显示出事件的发展方向与趋势.Sen's法可以计算时间序列的平均变化斜率,显示出存在明显上升或下降的时间序列的线性趋势.

为了分析极端降水指数的突变特性,采用Pettitt检验法和Mann-Kendall法(简称M-K法)对极端降水指数进行突变性分析.M-K法是水文序列中广泛使用的一种趋势检验方法[20-21].该方法是无参数的,很少受数据序列中异常值的干扰,允许在不进行任何特定分布假设时调查数据的长期趋势.Pettitt检验法[22]是一种与M-K法类似的非参数检验方法,直接利用秩序列检测突变点,时间序列中的突变现象不仅能够判断出突变点的位置及数量,还可判断这些变点在统计意义上是否显著.

3 结果及分析

3.1 趋势性分析

用滑动平均法和Sen's法分析尚家河水库雨量站和天福庙水库雨量站1978～2016年的极端降水指数变化趋势,利用Kendall秩次相关检验对变化趋势进行检验.其中滑动平均法取滑动长度为5,并绘制5年滑动平均变化曲线.

1)滑动平均法

计算并绘制极端降水指数五年滑动平均变化曲线并进行分析.

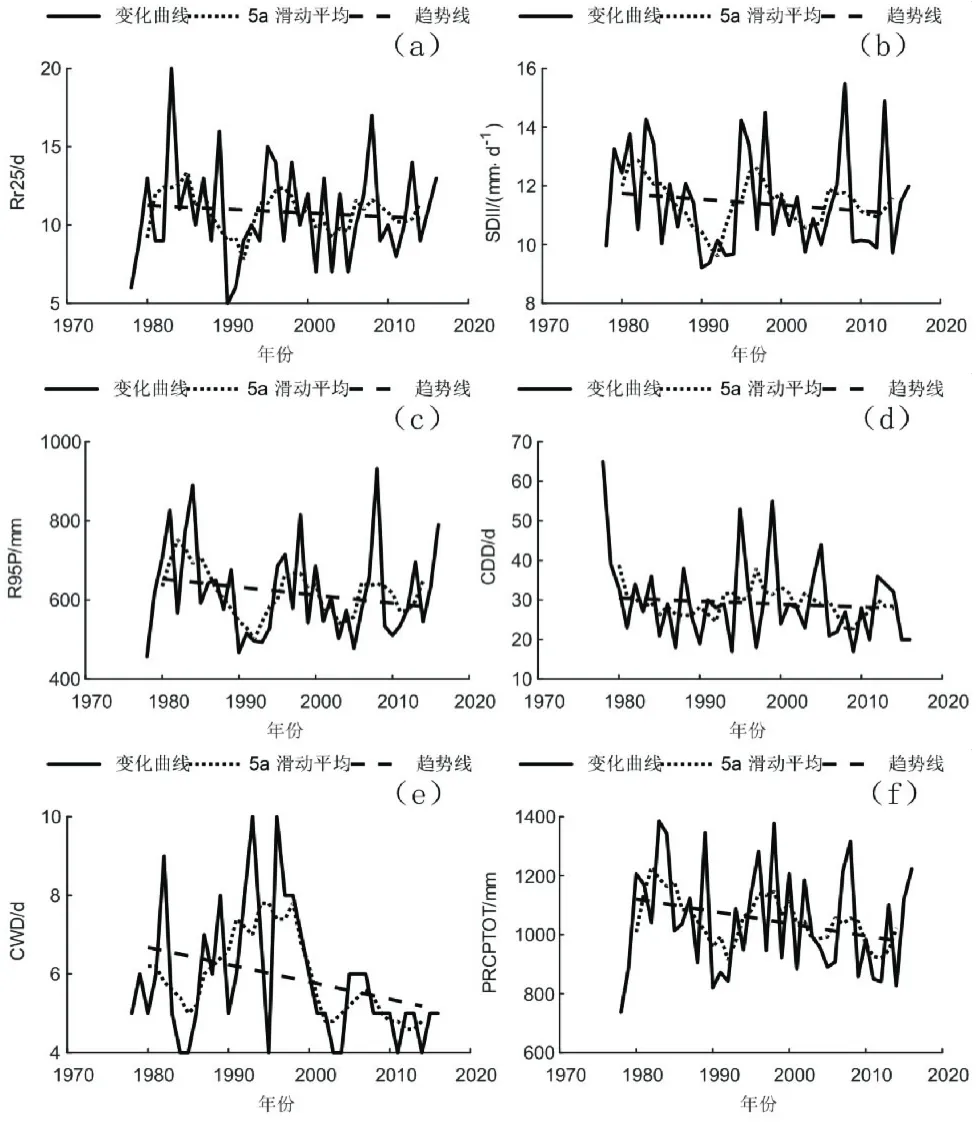
图2 尚家河水库雨量站极端降水指数变化趋势

由图2可知,尚家河水库雨量站大雨日数Rr25、年降水强度SDII、异常降水总量R95P、连续无雨日数CDD、连续降水日数CWD、年降水量PRCPTOT的最大值和最小值分别为20 d和5 d、15.48 mm/d和9.21 mm/d、931.8 mm 和457.2 mm、65 d和17 d、10 d和4 d、1 385 mm和737 m.极端降水指数变化曲线都呈下降趋势,Rr25下降趋势不明显,CWD变化曲线波动幅度逐渐减小.

图3 天福庙水库雨量站极端降水指数变化趋势

由图3可知,尚家河水库雨量站年降水强度SDII、连续无雨日数CDD、连续降水日数CWD变化曲线都呈下降趋势,CDD变化曲线下降趋势明显.大雨日数Rr25、异常降水总量R95P、年降水量PRCPTOT变化曲线呈轻微上升趋势.Rr25、SDII、R95P、CDD、CWD、PRCPTOT的最大值和最小值分别为18 d和4 d、15.06 mm/d和8.44 mm/d、951.7 mm 和379 mm、68 d和16 d、15 d和3 d、1532 mm和591 mm.

2)Sen's斜率估计

计算尚家河水库和天福庙水库极端降水指数的斜率,结果见表3.由表3可知,尚家河水库雨量站多年的年降水强度、异常降水总量、连续无雨日数、年降水量呈现减小趋势;大雨日数、连续降水日数趋势不明显.天福庙水库雨量站的多年来年降水量呈上升趋势;年降水强度、异常降水总量、连续无雨日数呈现减小趋势;大雨日数、连续降水日数变化趋势不明显.

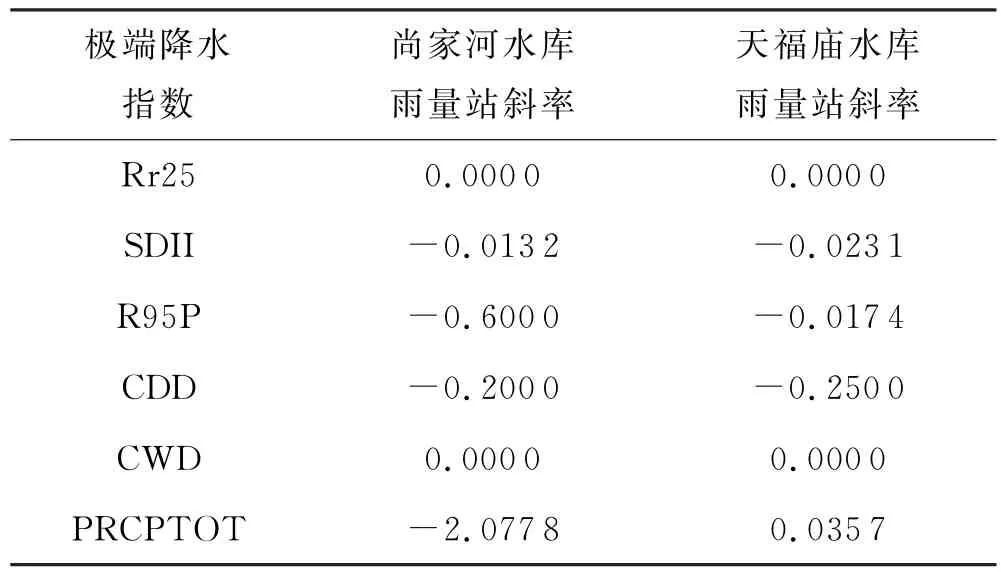
表3 极端降水指数变化斜率

3)Kendall秩次相关检验法

利用Kendall秩次相关检验法对尚家河水库雨量站和天福庙水库雨量站的6个极端降水指数进行分析,检验其趋势性是否显著.取信度水平α为0.05,Uα/2的值为1.96.各极端降水量指数计算结果见表4.

表4 Kendall秩次相关检验法统计量

由表4可知,尚家河水库雨量站的连续降水日数以及天福庙水库雨量站的连续降水日数、连续无雨日数的统计量|U|＞1.96,其多年变化趋势在0.05置信水平下显著,其他极端降水指数变化趋势不明显.

滑动平均法和Sen's法对极端降水指数变化趋势检验结果大部分是一致的,由于不同方法的原理不同,有个别极端降水指数变化趋势不一致.这个主要是由于滑动平均法可以排除周期变动和随机波动对时间序列的影响,显示出时间序列的发展方向与趋势,而Sen's法适用于存在明显上升或下降线性趋势的时间序列.所以对于没有明显线性趋势的时间序列,以滑动平均法的检验结果为准.

3.2 突变性分析

利用Pettitt法和M-K法对尚家河水库雨量站和天福庙水库雨量站的极端降水指数进行突变性分析,分析过程如下所示.

1)Pettitt法

利用Pettitt法对尚家河水库雨量站和天福庙水库雨量站1978～2016年6个极端降水指数进行突变性分析.计算结果见表5.

表5 Pettitt法统计量

由表5可知,两雨量站极端降水指数突变年份主要在2005年和2012年到2016年间.极端降水指数除天福庙水库的大雨日数外,突变不显著.

2)Mann-Kendall法

绘制尚家河水库雨量站和天福庙水库雨量站极端降水指数M-K突变检验曲线并进行变化特性分析.

由图4可知,尚家河水库雨量站大雨日数Rr25、年降水强度SDII、异常降水总量R95P、连续无雨日数CDD、连续降水日数CWD、年降水量PRCPTOT的UF线在1978～1994年间处于零线以下或附近(Rr25的UF线于1989年为0.08、CDD的UF线于1998年为0.01、PRCPTOT的UF线于1989年为0.13和1993年为0.003)、临界直线内,6个极端降水指数呈减少的趋势,趋势不显著;除CWD的UF曲线于1991～1994年和1996～2000年UF线在零线以上,临界线以内,整体上呈现上升趋势外,其他计算降水指数在1994年后整体上变化趋势不明显;Rr25、SDII、R95P、CDD、CWD、PRCPTOT的 UF和UB线在两临界线间存在交点,可能突变年份分别为2004年、2005年和2012年、2006年、2003年和2011年、1995年、2006年和2014年,突变显著.

图4 尚家河水库雨量站极端降水指数M-K曲线

由图5可知,天福庙水库雨量站大雨日数Rr25、年降水强度SDII、异常降水总量R95P、连续无雨日数CDD、连续降水日数CWD、年降水量PRCPTOT的UF线分别于1978～2004年(1996、1997年都为0.19)、1978～1995年(1992年为0.006)、1978～1995年(1993年为0.03)、1978～1989年、1978～1996年(1987年为0.33)、1978～2004年(2000年为0.33)处于零线以下或附近、临界直线内,呈减少趋势,趋势不显著;分别于2005年、2005年、2004年、1989年、1996年、2004年后处于零线以上,整体上呈上升趋势.Rr25、SDII、R95P、CDD、CWD、PRCPTOT的UF和UB线在两临界线间存在交点,可能突变年份分别为2004年、2004年(显著)、2004年、2003年和2013年(显著)、2003年(显著)、2004年.

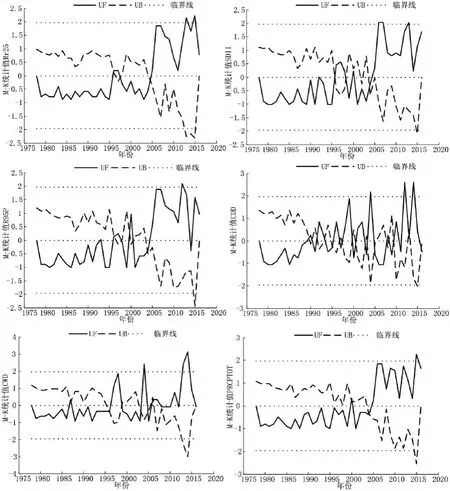
图5 天福庙水库雨量站极端降水指数M-K曲线

4 结 论

本文基于黄柏河流域1978～2016年逐日降水量资料,计算了大雨日数Rr25、年降水强度SDII、异常降水总量R95P、连续无雨日数CDD、连续降水日数CWD、年降水量PRCPTOT,利用滑动平均法、Sen's斜率估计、Kendall秩次相关检验法、Pettitt法和Mann-Kendall法分析了各指数的趋势性和突变性,研究黄柏河流域极端降水变化特性.主要结果如下：

1)两雨量站极端降水指数多年平均值除PRCPTOT相差较大外,其他极端降水指数多年平均值均相差不大.

2)多年来两雨量站Rr25变化趋势不明显,尚家河水库雨量站PRCPTOT呈现下降趋势,天福庙水库雨量站PRCPTOT呈现上升趋势,其变化趋势与尚家河水库雨量站R95P呈下降趋势,天福庙水库雨量站R95P呈上升趋势相对应.

3)两雨量站的CDD、CWD和SDII整体上呈下降趋势,且CDD和CWD下降趋势在置信水平0.05内显著.

4)两雨量站极端降水指数在1978～1990年左右呈下降趋势.天福庙水库雨量站大部分极端降水指数在2000年以后呈上升趋势.尚家河水库雨量站Rr25、SDII、R95P、CDD、CWD、PRCPTOT 分别在2004年、2012年、2006 年、2011 年、1995 年、2014 年发生突变.天福庙水库雨量站极端降水指数分别在2005年、2004年、2005 年、2003 年、2003 年、2005 年左右发生突变.

上述结果表明黄柏河流域极端降水指数多年平均值在空间上变化不大,这是由于黄柏河流域面积较小,位于上游的尚家河水库和下游的天福庙水库气候条件基本相同;年降水量的变化和异常降水总量的变化有关,两者变化趋势相同,这是由于异常降水总量是年内日降水量高于95%阈值降水量之和,在年降水量中所占比例较大;多年降水年内分布逐渐均匀,发生洪涝灾害的可能性减小;尚家河水库雨量站和天福庙水库雨量站极端降水指数在1978～1990年左右都呈下降趋势,两雨量站大部分极端降水指数在2003～2006和2011～2014年左右发生突变,这可能是受到近年来全球气候变化及人类活动的影响.