考虑损失的江河警戒水位拟定方法研究——以北流河为例

刘和昌，李世有，农珊，李善综

(1.水利部珠江水利委员会技术咨询中心，广东广州510611;2.云南省绿春县水务局，云南绿春662500)

警戒水位是各级政府科学、正确、高效地组织和指挥汛情发布、防汛抗洪工作的重要依据。在汛期，江河洪水上涨到控制站(水文或水位站)警戒水位时，堤防区或河段险情可能出现或逐渐增多，防汛部门随即进入防守戒备时刻。珠江流域各江河主要水文站基本虽已制定有各自的警戒水位，但有些警戒水位沿用了几十年，随着河流岸线的变化，城市建设的发展和防洪能力的加强，有些警戒水位已不适用，不符合当下的防汛形势，对警戒水位进行适时地复核调整是十分必要的。

目前，中国虽尚未形成统一的警戒水位拟定标准或规范，不少学者已进行过江河警戒水位理论与拟定方法的研究。叶林宜[1]认为警戒水位应是以控制站的多年平均年最高水位为基础，结合堤防工程的防洪能力、险工情况而定，对无堤防的城镇，则应视建筑物较低地面高程等情况而定；闵骞认为[2]警戒水位的确定，主要应从灾害学角度考虑，应重新建立以洪水风险与抗灾条件、减灾效益为基础的警戒水位体系；梁冰等[3]以鸭绿江流域临江水文站为例，介绍了水文站断面位置迁移时警戒水位、保证水位的换算方法；满媛等[4]分析了影响确定防洪控制断面和水文站特征水位的各因素；刘广成[5]根据对岸现状堤防威胁较大洪水、需加强巡堤查险和洪水出现期确定防洪断面警戒水位；董军[6]根据辽河滩唇与堤防关系、套堤分布特点等，认为采用高于大部分断面的流量作为河段警戒流量较为合适；林荷娟等[7]在堤防防洪能力、实际运用情况及水位频率分析的基础上，认为太湖警戒水位以重现期2～5 a较为合理；张延平[8]根据防护对象河段情况、防护工程情况及防护断面高程情况等，参照涨洪历时，对炼城水文站警戒水位进行了调整；刘卫林等[9]基于小流域水文计算和MIKE11水动力模型，提出了临界水位预警指标的确定方法；李善综等[10]从历史洪水资料中筛选出险洪水集，分情况在出险洪水集中选择对防洪不利的典型洪水来推求警戒水位。综合以上成果，警戒水位大都以保护对象开始受洪水威胁时的水位为参照，考虑一定的涨洪历时或防汛要求来确定。

江河警戒水位是洪水造成损失前的预设水位，达到警戒水位并不一定会造成较大的洪灾损失，实际中也经常出现有警无险或者险情很小的情况。因此，拟定江河警戒水位，不仅要掌握洪水特性，分析保护对象的防洪能力，研究警戒水位与洪灾损失之间的联系也是必要的。本文在前人研究成果的基础上，梳理了警戒水位拟定的影响因素，探讨了警戒水位拟定的原则，以防洪保护对象的起淹水位为参照，考虑警备时长，提出由洪水损失与洪水水位涨率的统计关系推求洪水水位涨率，进而拟定江河警戒水位。

1 研究方法

1.1 警戒水位影响因素

总结防汛经验和已有研究成果，警戒水位影响因素主要包括洪水特性、社会经济概况、防洪措施以及防汛工作要求等方面。

a) 洪水特性包括洪水过程、洪水水位涨率等。作为预警作用的水位，洪水水位涨率V是警戒水位拟定的重要因素，因每场洪水水位涨率不一样，V可认为是变量。

b) 防护区的社会经济情况包括人口、房屋、基础设施和农田等的高程和分布。江河两岸的房屋、基础设施或农田建成后，其最低高程即为开始受淹的水位Z受淹，一般为定值。每场洪水造成的损失S不一样，S是变量。

c) 防御洪水的措施包括防洪水库、堤防、水闸、蓄滞洪区等工程措施，以及水情测报系统等非工程措施，一般以所能防御标准洪水的水位Z防表示，一般为定值。

d) 防汛工作要求为防汛部门的工作需要，主要是预留一定的警备时长T，用于会商分析、预警发布、巡逻查险、人员部署、物资准备、财产转移等，一般为定值。

综上所述，江河警戒水位拟定的影响因素可概括为洪水水位涨率V、洪水损失S2个变量，以及受淹水位Z受淹、防御水位Z防和警备时长T3个常量。

1.2 警戒水位拟定原则

结合珠江流域防汛工作实践，根据警戒水位的定义和参考有关文献，警戒水位复核调整的原则归纳如下。

a) 现状为主，适度前瞻。以地区防洪现状为基础，适度考虑地区经济发展规划以及防洪体系规划对警戒水位拟定的影响，使复核后的警戒水位更加契合区域防洪工作实际，具有一定前瞻性。

b) 安全优先，科学高效。以保障区域防洪安全为基本前提，科学合理地拟定警戒水位，既要防止水位设置过高导致预警时间不足，也要避免水位设置过低增加巡逻查险、应急准备等的次数造成防汛资源浪费。

c) 统筹兼顾，上下协调。统筹河段左右岸、上下游和干支流的防洪需求，结合现状防洪能力以及历年损失情况，拟定有针对性的警戒水位方案，必要时可按上下游、左右岸分别确定。

d) 突出特点，因地制宜。对设有堤防的河段，以堤顶高程或临水水位作为参考，对无堤防河段，根据河岸出险情况及洪水上滩或者需要转移群众、财产时的水位参考，视河段洪水水位涨率、警备时长、洪水预报期等推求警戒水位。

1.3 警戒水位拟定方法

以受淹水位Z受淹或防御水位Z防为参照，考虑警备时长T，由洪水水位涨率v推求警戒水位Z警戒是实际中常用的方法。推求公式如下：

Z警戒=Z参照-vT

(1)

式中Z参照——采用的参照水位，m；v——洪水水位涨率，m/h；T——预留的警备时长，h。

a) 参照水位。根据“突出特点，因地制宜”的原则，若防护区内建有堤防、排涝设施等，以堤防、排涝设施可抵御的水位为参照，Z参照=Z防；若防洪防护区内未建有堤防、排涝设施等，以建筑物开始受淹的水位为参照，Z参照=Z受淹。

b) 洪水水位涨率。在式(1)中，参照水位Z参照、警备时长T均为定值，洪水水位涨率V的大小直接决定警戒水位Z警戒的取值。不同场次洪水的水位涨率不一样，实际中常选取对防洪不利的洪水场次，将其水位涨率均值作为采用涨率。本文从洪水灾害损失角度，分析洪水灾害损失S与洪水水位涨率V之间的相关性，探索由洪水灾害损失S来确定洪水水位涨率V大小的方法。

1.4 条件组合

在下垫面条件不变的情况下，洪水损失S的大小由洪水过程决定，洪水损失S与洪水水位涨率存在一定的相关性。联合概率分布是描述变量间统计关系的常用方法，近年兴起的基于Copula函数的多维联合分布理论，将变量间的联合分布分解为变量间的相关性结构和变量的边缘分布，为构建不同水文变量间的函数关系提供了较好的数学分析工具，并在水文领域得到了广泛的研究和应用[11]。

Copula函数是定义域为[0,1]均匀分布的多维联合分布函数，二维Copula函数可以表达为[12]：

F(u,v)=Cθ(FV(v),FS(s))=Cθ(g,h)

(2)

式中C——Copula函数；θ——Copula函数的参数；g=FV(v)、h=FS(s)——随机变量V、S的边缘分布。

相应的联合概率密度函数为：

f(x,y)=c(g,h)fV(v)fS(s)

(3)

式中c(g,h)——Copula函数的密度函数；fV(v)、fS(s)——随机变量V和S的概率密度函数。

统计历次洪水的洪水水位涨率和灾害损失，可得系列{[vi,si]}(i=1,2,…,n)，由此分析灾害损失与洪水水位涨率的相关性，构造洪水损失S与洪水水位涨率V的Copula联合分布函数Cθ(FV(v),FS(s))。当洪水损失S取设计值sP时，则存在一个条件概率分布：

(4)

此时，Fv|s(v)的密度函数为fv|s(v)=c(g,h)·fV(v)。fv|s(v)取最大值对应的vM值所形成的组合(vM,sP)称为条件最可能组合[13]，即洪水损失为sP时洪水水位涨率V的最可能取值；v的期望值E(v|sP)对应的组合(E(v|sP),sP)称为条件期望组合[11]，即洪水损失为sP时洪水水位涨率V的平均期望值。

2 实例应用

西江一级支流北流河某镇临河而建，辖20个行政村、1个社区，总人口7.5万人，当前水文站警戒水位设立较早，是根据当时的防洪能力和洪水淹没经验大体上确定的，随后河道内陆续有水利工程兴建。据统计，在现有警戒水位下，平均每年发生4.43次超警戒洪水，频率较高，巡逻查险次数较多，但大多数超警洪水并未造成较大的生命财产损失，现对该警戒水位进行复核调整。

2.1 影响因素分析

a) 洪水特性。水文站集水面积9 111 km2，所在流域多年平均降雨量约为1 620 mm，汛期4—9月降雨量约占全年雨量79%。由于受地形的影响，出现的较大洪水大部分由台风雨造成，形成的洪水往往峰高量大，一次洪水过程约11 d。该水文站实测大断面见图1，水位～流量关系见图2。

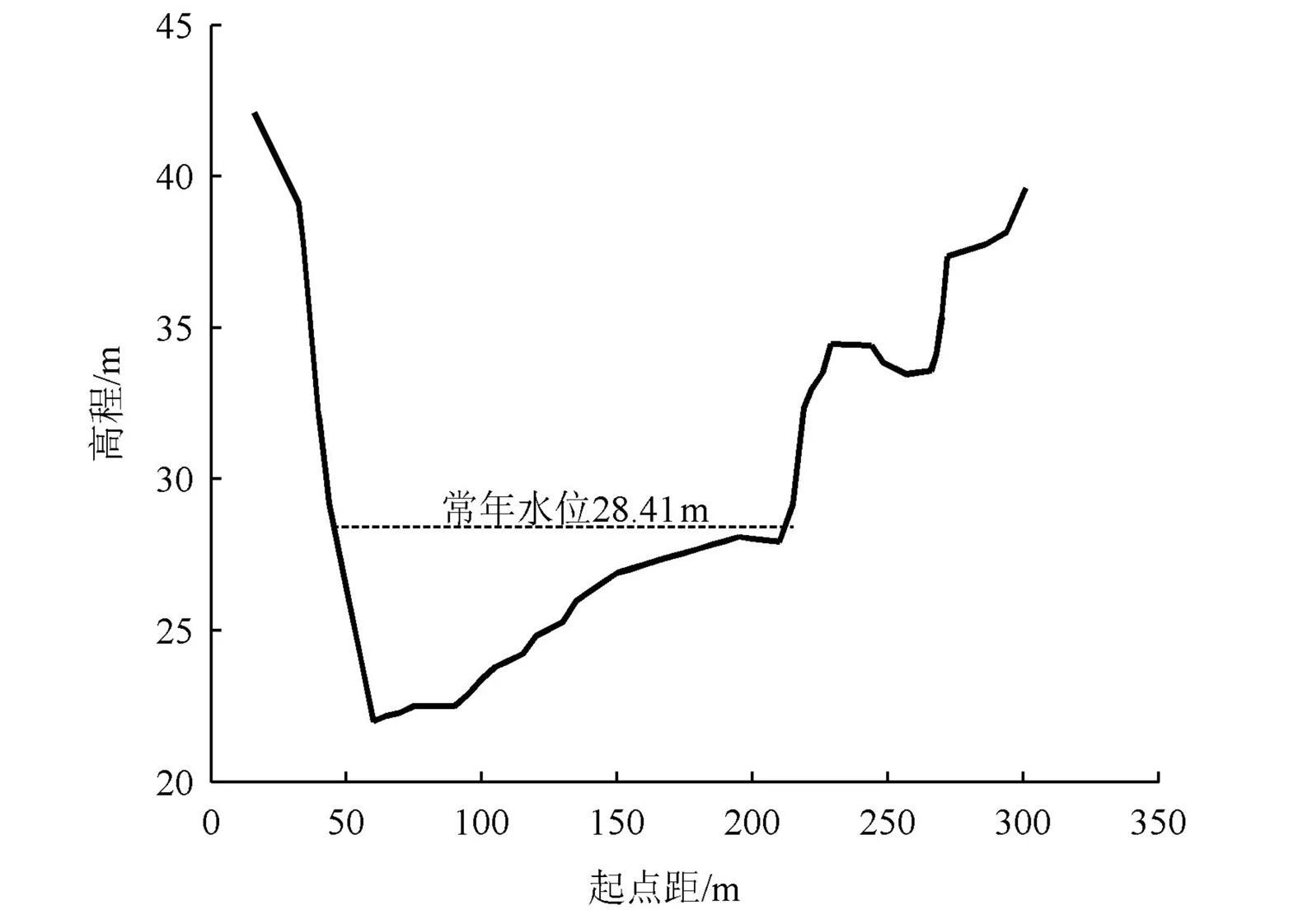
图1 水文站实测大断面

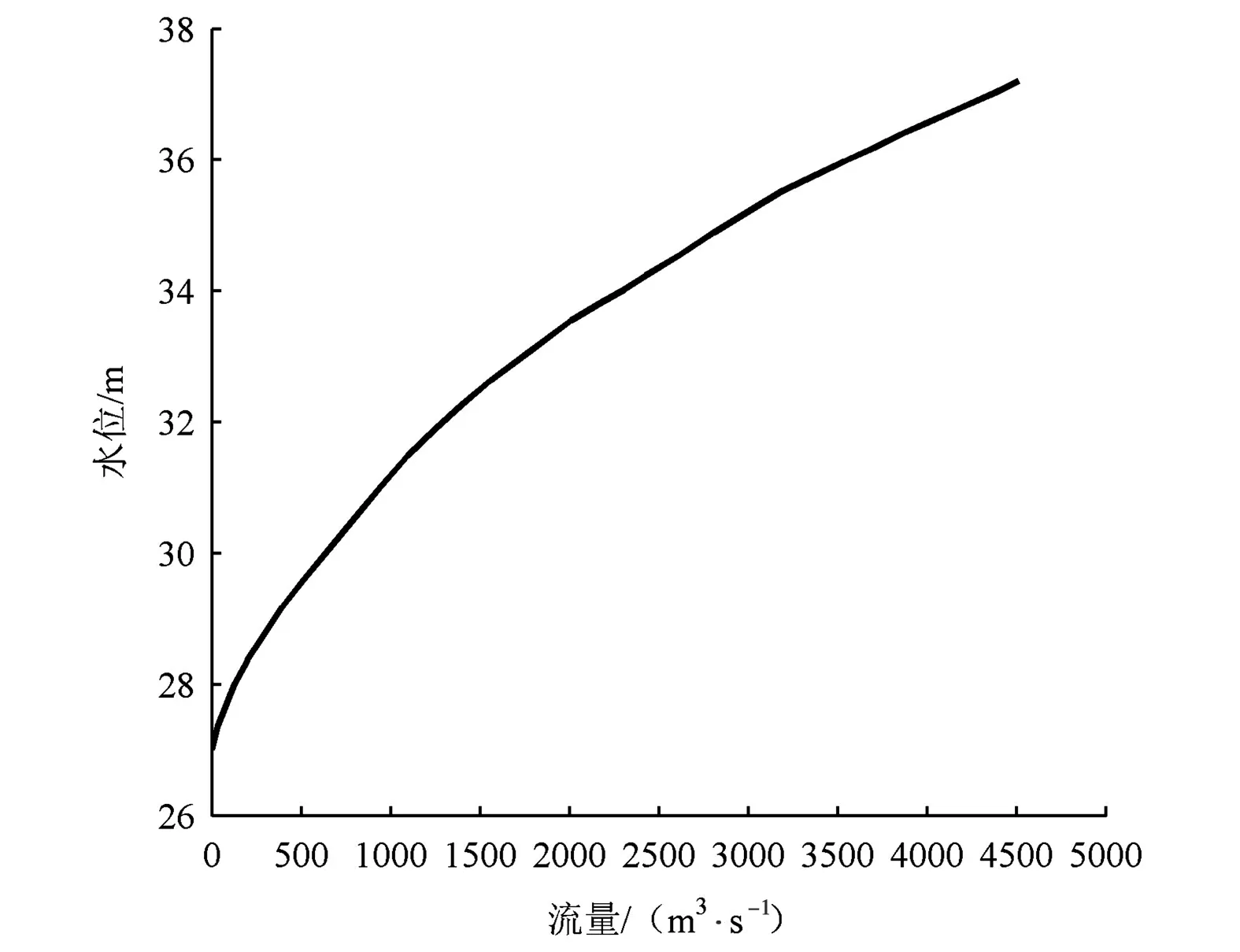
图2 水文断面水位～流量

b) 社会经济分布。该镇镇区在某水利枢纽坝址上游4 km的左岸，主街道呈T字形，地势低点高程约为34.7 m；下游河段主要为电站回水淹没区，水位34 m时部分房屋开始受淹。按照警戒水位拟定“适度前瞻”的原则，查阅该镇总体规划报告，可知镇区近期主要沿现状用地向西北和东南推进，远期建设继续向西北发展，均远离河道，故该防护区的受淹水位Z受淹可确定为34 m。

c) 防洪措施。防护区除水利枢纽在其库区淹没范围内布置了部分洪水防护工程外，河道内未有建成的、在建的或近期规划新建的防洪堤、排涝设施等防洪工程。水文站上游3 km处有一以发电为主的水利枢纽，下游10 km处有一电站。上游水库淹没的房屋迁移线采用10年一遇洪水回水标准，防洪堤坝坝顶高程40 m。根据水位流量关系，10年一遇洪水对应水文站水位为38.13 m，即该镇镇区河段可防御洪水水位Z防为38.13 m。经调查，防护区水情测报系统尚不完善，测报能力较弱。

d) 防汛工作要求。结合防护区防汛部门工作需求，洪水自达警戒水位涨至镇区起淹水位止，一般预留3 h的警备工作时间，即T=3 h。

2.2 警戒水位推求

a) 确定参照水位。上游镇区河段可防御洪水水位Z防为38.13 m，下游临河房屋开始受淹水位Z受淹为34 m，为保障安全，将警戒河段内出险的最低水位确定为参照水位，即Z参照为34 m。

b) 确定边缘分布。同一水文年中可能有多场洪水超警，并造成洪水损失，本文采用年多个样本法提取洪水水位涨率样本vi和相应的洪水损失样本si。对特定区域，参照水位Z参照和警备时长T是常量，每场洪水警戒时段的水位涨率应是参照水位Z参照前T小时的平均涨率，若记Z参照前T小时的水位为Zi，则根据式(1)，可得该场洪水的水位涨率vi=(Z参照-Zi)/T。在当前社会经济分布和防洪工程措施下，结合已有记载的洪水损失和最高洪水位，调查分析不同洪水位下的洪水损失，由每场洪水的最高水位可估算本场洪水的洪水损失si。根据2002—2015年实测场次大洪水资料，由年多个样本法可取得{[vi,si]}的样本共31组。采用P-III曲线对洪水水位涨率系列{vi}、洪水损失系列{si}进行函数拟合，得到边缘分布FV(vi)、FS(si)及概率密度函数fV(v)、fS(s)，统计参数见表1，频率曲线见图3、4。

表1 边缘分布统计参数

c) 构建联合分布函数。由洪水水位涨率和洪水损失的组合系列{[vi,si]}，采用线性相关系数、

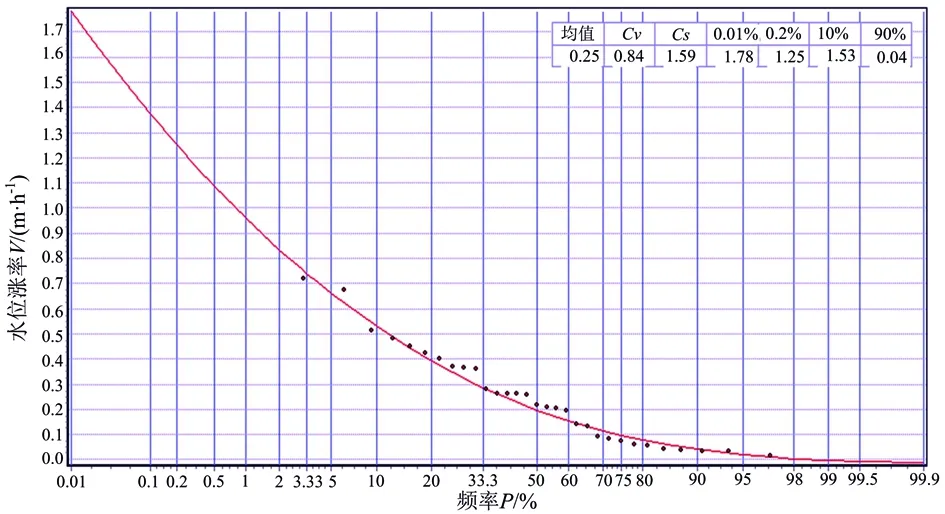
图3 水位涨率频率曲线

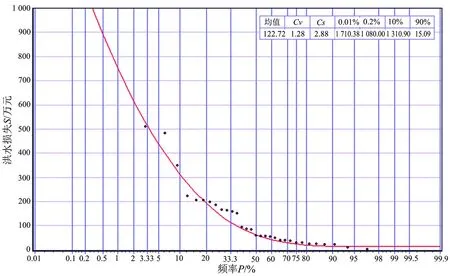
图4 洪水损失频率曲线

Kendall秩相关系数和Spearman秩相关系数分析两者的相关性，结果见表2。在Copula函数簇中，Gumbel-Hougaard Copula[14]适于变量间存在正相关的情形，能描述变量间的上尾相关性[15]，本文选用该函数作为洪水水位涨率V与洪水损失S联合分布函数，函数参数θ可由相关系数求得为4.0，联合分布经验与理论概率拟合情况见图5，拟合较好。由此，构建S与V的Copula联合分布函数Cθ(FV(v),FS(s))及其概率密度函数cθ(FV(v),FS(s))。

表2 洪水水位涨率与洪水损失的相关性系数

d) 确定洪水水位涨率。以历次大洪水水位涨率的均值作为拟定警戒水位的洪水水位涨率，得到采用涨率为0.248 m/h；在平均洪水损失123万元的条件下，由S与V的条件概率密度函数cθ(FV(v),FS(s))fV(v)，可求得洪水水位涨率的条件最可能值0.287 m/h和条件期望值0.289 m/h。

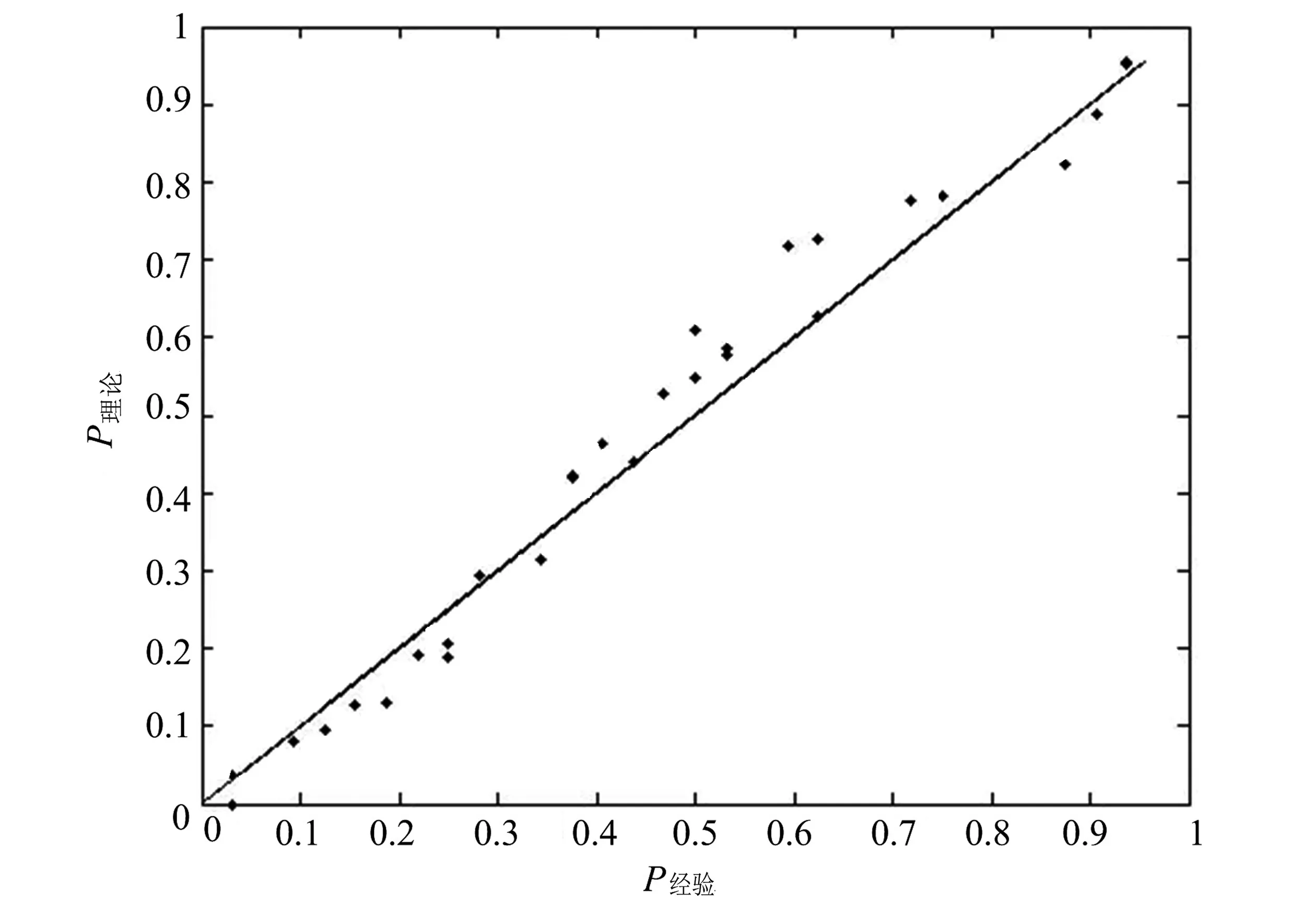
图5 水位涨率与洪水损失联合分布概率联合分布

e) 拟定比选方案。根据式(1)，可求得洪水水位涨率的条件最可能值、条件期望值和均值所对应的警戒水位分别为33.14、33.13、33.26 m。为方便管理、宣传等，在保证防洪安全的前提下，拟定警戒水位为33.1、33.2、33.3 m。

f) 推荐警戒水位。根据2002—2015年洪水资料，在33.1、33.2、33.3 m警戒水位方案下，年均超警次数由原来的4.43次分别降为1.79、1.57、1.50次;警戒水位涨至起淹水位34 m的次数占总超警次数的比例由原来21.0%提高至52.0%、59.1%和61.9%。3种方案都大大减少不必要的警戒次数，有利于节约防汛成本。在洪水位达起淹水位的洪水中，33.1、33.2、33.3 m方案警备时长达3 h的比例分别为69.2%、69.2%和53.8%，其中33.1、33.2 m警戒水位方案的警备时长达3 h比例较高，对防汛工作和镇区防洪安全影响较小，更偏安全。此外，按照“上下协调”“科学高效”的原则，33.1 m方案与下游电站的防汛预警更为协调。因此，推荐水文站警戒水位为33.1 m，相应流量为1 790 m3/s。

3 结论

a) 洪水水位涨率对警戒水位的拟定关系重大。本文在分析警戒水位影响因素的基础上，基于Copula函数建立洪水水位涨率与洪水损失的条件概率分布函数，由洪水损失推求洪水水位涨率的条件概率值，并以起淹水位为参照、以警备时长为控制，提出考虑洪水损失的江河警戒水位拟定方法，可充分保障防护区的防洪安全，有效发挥水位的警戒作用。

b) 水文变量间的统计关系需建立在物理成因上。对同一防洪保护区，洪水过程直接决定洪水损失的大小，洪水灾害损失与洪水水位存在物理成因关系，实例中统计的起涨水位至最高洪水位的涨率系列与洪水损失存在较强的正相关关系，这与实际相符。

c) 防御水位是警戒水位拟定的重要参照。随着防洪工程体系的完善，防护区内、上下游河段若兴建了水库、堤防等改变区域防洪能力的工程，防御水位将发生变化，为确保防汛工作的合理、高效，此时警戒水位应再次复核调整，并及时向社会公布。