基于时间序列预测的印度2020年乘用车销量研究
2019-10-16罗智恒
罗智恒


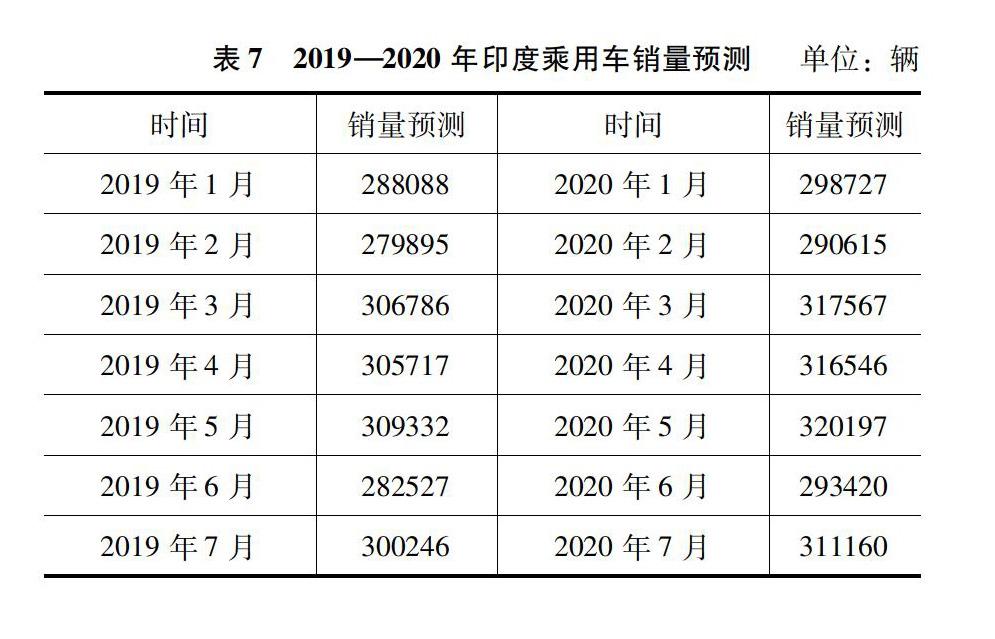
[摘 要]为了给汽车业“出海”印度参考,文章利用时间序列预测印度乘用车2020年销量。首先,提出了利用时间序列预测销量的研究思路。其次,利用印度乘用车2010—2018年销量数据,按研究思路预测出印度乘用车2019年销售3492170辆,同比增长2.87%;预计2020年销售3622561辆,同比增长3.73%。最后,用2019年1—3月的实际销售数据,与预测数据对比得出预测误差在5.20%内,验证了预测模型的精度。
[关键词]印度乘用车销量;预测;时间序列;2020年;ARMA
[中图分类号]F426
1 前 言
印度作为“金砖四国”之一,联合国人口署2017年公布其人口为13.39亿[1], 世界第二;据国际货币基金组织消息,2018财年GDP为2.69万亿美元,排行世界第7 [2];2018年乘用车销量为339.4万辆, 千人汽车拥有量不足30辆[3],不但远低于美国千人汽车拥有量800辆,也小于中国千人汽车拥有量170辆[4],汽车业拥有巨大发展空间。
但印度存在“三个短缺”:持续的国际贸易赤字、长期的政府预算赤字,以及欠发达地区的发电和配电基础设施[5];同时2018年印度人均GDP仅为2016美元,世界排名146位(同期中国人均GDP为9633美元,世界排名76位)[2],国家社会的发展水平和发展程度偏低,使其汽车业发展存在不确定性。为此文章尝试利用时间序列预测2020年印度乘用车销量,给国内各大整车厂进入印度市场提供参考。
时间序列是将某一个变量或指标在不同时间上的不同数值按照时间的先后顺序排列而成的数列。Box 和Jenkins在20世纪70年代首次提出利用时间序列进行预测[6],主要利用平稳时间序列的统计性质不随时间原点的推移而变化的特性。
2 研究思路
文章预测印度2020年乘用车销量研究思路如图1所示。
2.1 时间序列
将印度乘用车每月销量数据按先后顺序导入。
2.2 平稳
判断一个时间序列是否平稳,通过自相关系数及其图形,可以初步判断一个时间序列的平稳性。如需定量地判断时间序列的平稳性,则可采用Dickey-Fuller(DF检验)单位根进行检验。如果时间序列平稳,就进行第3步平稳时间序列的步骤;如果时间序列不平稳,就进行第7步平稳化。
2.3 平稳时间序列
如时间序列平稳,就可以利用AR,MA,ARMA进行预测。
2.4 模型识别
从AR,MA,ARMA中选择合适的时间序列模型。常用的模型识别方法有:利用自相关系数、偏相关系数图进行模型识别;计算扩展的自相关函数(EACF)并利用其估计值进行模型识别[7]。
2.5 参数估计
模型所含的未知参数,通过时间序列确定其最优估计,一般采用的估计优化准则为矩估计、极大似然法和最小二乘法[8]。然后,进行第6步对模型进行评估。
2.6 评估
通过分析拟合模型的残差和过度参数化的模型,可以保证拟合模型的优度同时又不过拟合[8] 。如果模型被正确识别,参数估计足够接近真实值,则模型残差就应该近似白噪声,服从独立、同分布的零均值和相同标準的正态分布[8]。如通过评估,则可以到第12步进行预测数据;如没有通过评估,则进行第4步模型识别,调整模型。
2.7 平稳化
平稳化常用方法有:加法模型、乘法模型、混合模型和差分模型[9]。若一时间序列能够通过差分的方式平稳化,则称其具有单位根。如一个时间序列具有单位根,则它是非平稳的。如平稳化成功后,则回到第3步;如平稳化失败,则到第8步进行非平稳时间序列分析。
2.8 非平稳时间序列
如果时间序列不能平稳化,则用非平稳时间序列进行预测。常用的非平稳时间序列预测模型有:指数平滑法[10],但其只适合短期预测。
2.9 模型识别
指数平滑法分为一次平滑法和多次平滑法。销量预测中主要运用多次平滑法中的二、三次指数平滑法。然后进行第10步。
2.10 参数估计
指数平滑法中,需要确定的参数为平滑系数。然后进行第11步。
2.11 评估
通过平均误差, 平均绝对误差和均方差来评估模型的拟合效果[10]。如通过评估,则可以进行第12步进行预测数据;如没有通过评估,则进行第9步模型识别,调整模型。
2.12 预测数据
根据模型预测将来的数据值,并进行预测精度分析:一是模型对现有数据的拟合程度;二是模型对将来预测数据的准确程度,通常采用后验预报方法进行精度分析[9]。
3 具体实例
3.1 时间序列
由中国汽车工业协会、MarkLines获得2010—2018年印度乘用车每月销量如表1所示,印度乘用车销量时间序列X(以下简称时间序列X),记 Xi为时间序列第i个月销量。
3.2 平稳
对时间序列是否是平稳时间序列进行检验。利用自相关系数
(1)式中rp是时间序列X的p阶样本,Xt是时间序列X第t个月销量,X-是时间序列X的均值。根据上式,利用R软件计算各点p的自相关系数,并绘制相关系数如图2所示,从图中可以发现时间序列的自相关系数超过置信区间(图2中虚线内区间),可以判定时间序列X非平稳。
3.3 平稳化
3.4 模型识别
3.5 参数估计
在确定时间序列Y的模型之后,采用最小二乘法使参数et平方和达最小值(如式(4)所示)的方法:
带入2011—2018年样本数据进行模型的参数估计,由R软件拟合出时间序列Y ARMA(1,1)模型估计结果如表3所示。
3.6 评估
再确定模型具体形式,利用残差进行评估检验。残差如式(6)所示:
4 结 论
利用2010—2018年印度乘用车销量数据,首先对其季节差分获得平稳时间序列,然后识别出模型ARMA(1,1),并进行参数估计及检验,最后利用此模型预测印度乘用车2019—2020年销量。用2019年1—3月的实际销售数据,对比预测数据得出预测误差在5.20%内。说明此方法进行的预测具有一定的精度。同时如果数据更新,可以用文章的方法继续预测后续销量。
参考文献:
[1]United Nations Department of Economic and Social Affairs Population Division . World Population Prospects: The 2017 Revision[EB/OL]. (2019-07-1)[2019-04-09].https://population.un.org/wpp/Download/Standard/Population/.
[2]IMF. 2018年世界经济展望排行榜单版[EB/OL].(2018-10-09) [2019-04-09].https://xw.qq.com/cmsid/20181022B00EVC/20181022B00EVC00.
[3]張冬梅.逆势增长5.32%,印度2021年将成全球第三大车市[EB/OL].(2019-01-018)[2019-04-09].http://www.sohu.com/a/289976869_120044219.
[4]孙杰.千人汽车保有量170辆左右 国家发改委:消费升级趋势依然强劲[EB/OL].(2019-1-29)[2019-04-09].https://baijiahao.baidu.com/s?id=1623968075621898571&wfr=spider&for=pc.
[5]白莉.2020年印度将成世界第三大汽车市场[J].中国汽车界,2011(10):26.
[6]GEORGE E P BOX, GWILYM M NKINSJE, GREGORY C REINSEL. 顾岚,主译.时间序列分析:预测与控制[M].北京:中国统计出版社,1997.
[7]TSAY R,TIAO G. Consistent estimates of autoregressive parameters and extended sample autocorrelation function for stationary and nonstationary ARMA models [J]. Journal of the American Statistical Association, 1984,79 (385):84-96.
[8]JONATHAN D CRYER, KUNG-SIK CHAN.时间序列分析及应用R语言[M].北京:机械工业出版社,2011.
[9]冯康.数值计算方法[M].北京:国防工程出版社,1978.
[10]张忠平.指数平滑法[M].北京:中国统计出版社,1996.
