活塞风作用下双竖井隧道内微波折射率结构常数的估算模型*
2019-10-16孙华清赵恒凯
孙华清 赵恒凯
(上海大学通信与信息工程学院,200444,上海//第一作者,硕士研究生)
无线电波传播会受到大气湍流的影响,进而影响无线通信的质量。大气折射率结构常数是一个反映湍流强度的物理量,可以用来描述无线电波受湍流影响程度。
为了深入了解大气湍流对光波及电波传输的影响,文献[1-5]等探讨了多种环境下的湍流强度,建立了相应的折射率结构常数估算模型,为湍流领域的研究奠定了一定的理论基础。
本文在Monin-Obukhov相似性原理的基础上,对双竖井隧道内由于列车运行产生的复杂空气湍流场进行了分析探究和建模,推导出一种适用于双竖井隧道内的折射率结构常数估算模型,为研究隧道内大气湍流对无线电波传播特性的影响提供理论参考。
1 湍流折射率结构常数估算模型
1.1 湍流折射率结构常数及与其结构参量的关系
在大气环境下,大气折射率n可以表示为
n=1+N×10-6
(1)

(2)
式中:
N——大气折射率指数;
T——大气温度,K;
P——大气压强,hPa;
e——水汽压,hPa;
Dn——折射率梯度,在微波频段取77.6 K/hPa;
Hn——高度常数,在微波频段取4 810 K/hPa。
当T=288.15 K时,饱和水汽压es=17.12 hPa,相对湿度HR取值0~100。依据气象统计资料[6],水汽压e的计算式为:
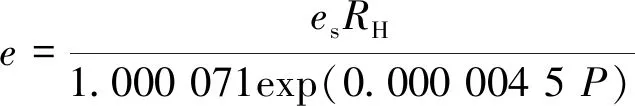
(3)
其中,e单位为hPa。
比湿q也可以表示为[7]:

(4)
结合式(2)—(4)可得,微波段大气折射率的简化计算式为:

(5)
根据Kolmogorov的局部均匀各向同性原理,在湍流惯性子区间内,空间两点间的折射率结构函数可以定义为:
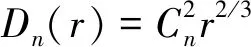
(6)
式中:
r——空间两点间距离;


(7)
式中:
AT——大气折射率对温度的偏导;
Aq——大气折射率对湿度的偏导;
CT——大气折射率温度结构函数;
Cq——大气折射率湿度结构函数;
CTq——温湿度相关结构函数。
在微波段,有

(8)
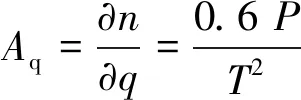
(9)


(10)
式中:
fT(z/L)、fq(z/L)及fTq(z/L)——分别为与温度、湿度及温湿度相关的稳定度参数经验公式。
rTq——温湿度相关系数,取值与波文比Bo的正负有关;当Bo≥0时,rTq≈0.8;当Bo<0时,rTq≈0.5。
z——高度。
L——M-O(Monin-Obukhov)长度,z/L为稳定度参数。有:
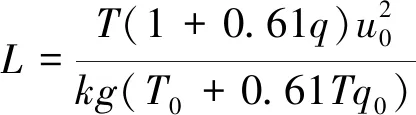
(11)
式中:
k——卡尔曼常数,通常取0.4;
g——重力加速度;
u0——摩擦速度。
根据文献[10],在不稳定层结条件下,有:

z/L<0
(12)
1.2 双竖井隧道内的活塞风对的影响
活塞风速大小会直接影响区间隧道内的温度及湿度状况。列车在区间隧道内运行时,由于隧道壁面的限制,列车对隧道空气产生推动作用,列车车头处呈现正压,车尾部分则为负压,在这样的压差作用下,一部分气体被推出隧道出口和竖井出口,一部分则从车头经过列车和隧道间的环状空间流到车尾。
当列车在长度为L2区段行驶时,由连续性方程得
Av=A5v5+Av3
(13)
或
Av=A4v4+Av2
(14)
式中:
A——隧道平均横截面积;
A4——左侧竖井横截面积;
A5——右侧竖井横截面积;
v——长度为L2区段气流速度;
v2——长度为L1区段气流速度;
v3——长度为L3区段气流速度;
v4——左侧竖井内气流速度;
v5——右侧竖井内气流速度。
如图1所示,可先建立列车前缘断面1-1与列车尾部断面6-6之间的能量方程:
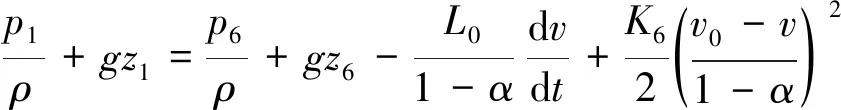
(15)
式中:
λ——沿程阻力系数;
K6——气流在环状空间中的阻力系数;
pi——在隧道i处的局部阻力压降;
zi——隧道i处的高度;
ρ——空气密度;
v0——隧道空间下垫面风速;
α——隧道阻塞比。

图1 列车在隧道双竖井之间行驶示意图
建立列车前缘断面1-1与隧道出口断面3-3之间的能量方程:
式中:
ξ出——隧道出口局部阻力系数。
建立左竖井进口断面4-4与隧道断面7-7之间的能量方程:

(17)
式中:
K13——气流由左竖井汇入隧道长度为L2区段的阻力系数;
ξ47——左竖井中的气流汇入隧道长度为L3区段的局部阻力系数。
右竖井进口断面5-5与隧道断面8-8之间的能量方程为:

(18)
式中:
K14——气流进入左竖井隧道的阻力系数;
ξ58——右竖井中的气流汇入隧道段长度为L3区段的局部阻力系数。
综合式(15)—(19),可以求得长度为L2区段中的活塞风速v活为:

(19)
式中:
ξtot——双竖井隧道的总阻力系数。
K——双竖井隧道的总活塞作用系数。有:

(20)
1.3 双竖井隧道内M-O长度的确定及建模
根据Monin-Obukhov相似性理论,双竖井隧道内风速v、温度T以及比湿q的无量纲轮廓线可分别表示为
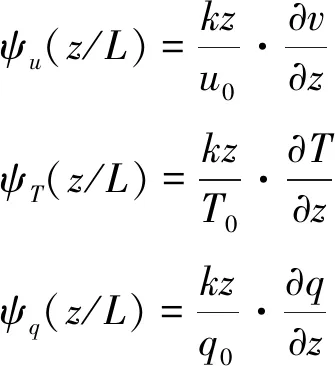
(21)
u0、T0、q0可以分别表示为:

(22)
式中:
Δv、ΔT、Δq——隧道空间一点z1与参考点z0之间的风速差、温度差和湿度差。
根据文献[11-12]的经验公式可知:
在不稳定大气环境下,即z/L<0时

(23)

(24)
将式(23)—(24)代入式(11),可以得到不稳定大气环境下双竖井隧道内的M-O长度为
(25)
综上所述,结合式(7),可将双竖井隧道的大气折射率结构常数表示为:

(26)
综合式(8)、(9)、(24)及(25),可得活塞风作用下的双竖井隧道内的大气折射率结构常数表达式:

(27)
其中,Δv=v活-v0,v活为活塞风速,f(T,q,p)是双竖井隧道环境下与温度、湿度及压强相关的函数:
1.2rTqPTΔTΔq(77.6×10-6PT+1.2q)+(0.6PTΔq)2]
(28)
2 仿真试验
2.1 仿真试验基本数据
基于上海轨道交通2号线部分区间隧道的数据,使用MATLAB仿真软件,对隧道环境内的微波段的折射率结构常数进行仿真分析。
上海轨道交通2号线全长约27 km,其车辆、供电、接触网及通信等系统由德国戴姆勒-奔驰交通公司和西门子公司提供。列车为8节编组,每节车厢的长、宽、高分别为23.54 m、3.00 m、3.80 m,列车运行速度约为75 km/h。取南京西路站—静安寺站区间隧道作为研究对象。隧道内高度为2.00 m,长度约为1.37 km,平均截面面积为30.15 m2。隧道内参考面温度T0=288 K,参考面上的水平风速为2 m/s,大气压强P取1 013 hPa。由于隧道内底部湿度较大,参考面的相对湿度取HR=60。双竖井隧道内沿程阻力系数λ取0.05,双竖井隧道局部阻力系数ξtot取0.5,温度差(T-T0)为活塞风作用下的隧道内空气与参考面的气温差。
2.2 不同活塞风速条件下的仿真
图2是在双竖井隧道内不同活塞风速条件下,大气折射率结构常数随着温度差的变化曲线。
由图2可见,当温度差的绝对值较小时,即|T-T0|<10,随着|T-T0|的增大,隧道内大气折射率结构常数大幅增大。可见,温度差变化对双竖井隧道内的大气折射率结构常数影响显著。当温度差在一定范围时,随着活塞风速的增大,双竖井隧道内大气折射率结构常数增大。与活塞风速变化相比较,温度变化对于大气折射率结构常数变化的影响更加显著。

图2 不同活塞风速v下温度差和大气折射率结构常数之间的关系
2.3 不同竖井条件下的仿真
为了探究双竖井隧道环境对于湍流强度的影响,运用上述参数,并取活塞风速为12 m/s,隧道长度均为1 370 m,对不同竖井条件情况下的折射率结构常数进行仿真比较。仿真结果如图3所示。
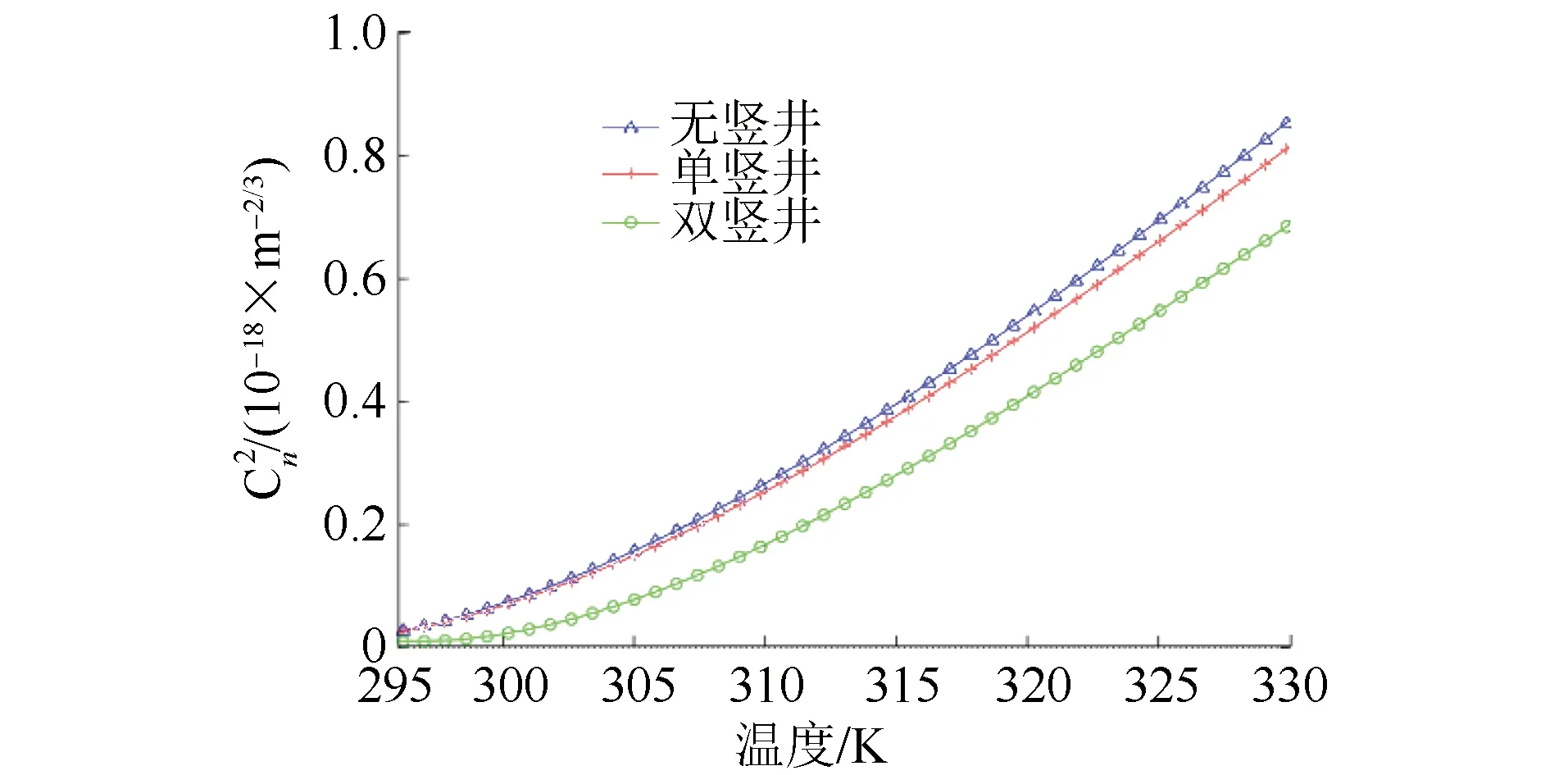
图3 不同竖井条件下隧道温度与大气折射率结构常数之间的关系
由图3可知,与无竖井、单竖井隧道环境比较,双竖井隧道内湍流强度较后两者都小,且温度升高时,双竖井的通风效果更加明显,因此,双竖井有效降低了隧道内湍流强度,有利于无线通信系统性能的提高。
2.4 不同双竖井间距条件下的仿真
取活塞风速为12 m/s,分别对双竖井间距Ld为0.5 km、1.0 km及1.5 km的隧道进行不同温度差的仿真分析。仿真分析结果见图4。
由图4可以看出,随着双竖井间距的不断增加,隧道内湍流强度也不断增大。这是因为双竖井间距变大后,隧道内通风效果变差,使列车周围气流运动空间相对变小,单位体积空间内空气温湿度的变化加快。此外,竖井间距的调整可以大幅改变大气折射率结构常数。只有当双竖井间距趋于极限值时,大气折射率结构常数变化才不再明显。这是因为间距足够大时,双竖井通道类似于无竖井隧道,不再有明显的通风效果。
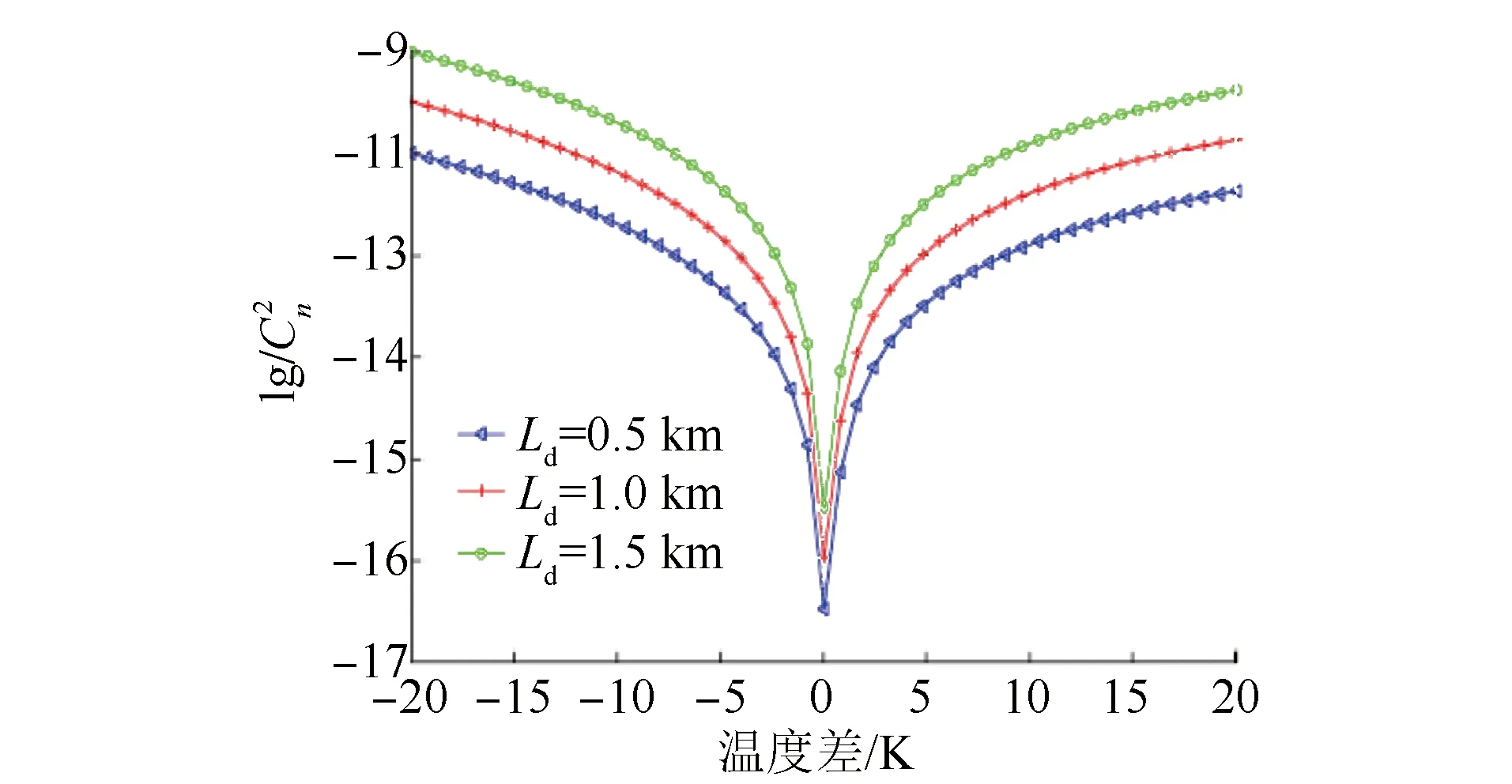
图4 不同双竖井间距下温度差和大气折射率结构常数之间的关系
为了进一步探究活塞风速与湍流强度的关系,还对双竖井间距Ld为0.5 km、1.0 km及1.5 km的隧道,针对不同活塞风速进行仿真分析。仿真分析结果见图5。

图5 不同双竖井间距下活塞风速度与大气折射率结构常数之间的关系
由图5可见,双竖井隧道环境中,随着列车速度的增大,活塞风速度增大,加剧了隧道内湍流变化,致使大气折射率结构常数呈上升趋势。
由图5还可看出:竖井间距对于活塞风的作用效果也造成影响,竖井间距增大则活塞风所导致的大气折射率结构常数变化的动态范围趋小;当活塞风速足够大时,隧道内的大气折射率结构常数已经趋于极限值,故双竖井间距对于隧道内湍流强度的影响也不再明显。
3 结语
本文利用近地层相似形理论以及Bulk方法,采用Frederickson公式,结合双竖井隧道活塞风的运动特性,计算出温度结构常数、湿度结构常数和温湿度结构函数,建立了双竖井隧道不稳定空气环境下的大气折射率结构常数估算模型。
通过对实例项目的仿真分析可知:
1) 双竖井隧道环境下空气湍流大气折射率结构常数的数量级为10-15~10-11;双竖井有效降低了隧道内湍流强度,与单竖井隧道相比较,湍流强度至少降低了2个数量级。
2) 阻塞比对于双竖井隧道的影响比单竖井隧道更弱;竖井间距对于活塞风的作用效果也造成影响,竖井间距增大则活塞风所导致的大气折射率结构常数变化的动态范围趋小;而当活塞风速足够大时,双竖井间距对于隧道内湍流强度的影响也不再明显。
3) 双竖井隧道环境下,列车速度在超过一定范围后,或者列车速度较大时,其对湍流强度的影响将不再明显。
综上所述,通风双竖井能有效降低大气折射率结构常数,进而降低湍流对电波传播的影响,有利于隧道内无线电波的传输。
