现代有轨电车组合定位模型及其仿真试验
2019-10-16吴学杰张梦乡
胡 巧 吴学杰 张梦乡
(西南交通大学牵引动力国家重点实验室,610031,成都//第一作者,硕士研究生)
现代有轨电车常采用的GPS(全球定位系统)定位,是一种全球、全天候连续的三维定位,能为各类用户提供动态目标的位置、速度和时间信息[1]。单一的GPS定位容易受到线路沿途的干扰,形成定位的盲点,不能实现准确连续的实时定位。因此,有轨电车实际运行中往往采用GPS与其他定位方式相结合的组合定位。文献[2]提出基于BP神经网络的GPS-RFID(射频识别)定位方式,虽有效地提高了定位精度,但网络训练算法具有一定的难度。文献[3]提出了GPS和ZigBee(紫蜂)的有轨电车组合定位方式。其中ZigBee定位设备网络容量大,定位精度也很高,频段较灵活,但是ZigBee的寻址机制可靠性较低,存在很多潜在问题。文献[4]研究出基于高压脉冲轨道电路和RFID的有轨电车定位,其抗干扰能力强,易于实现电子化,颇具前景。
本文在文献[5]提出的GPS和航位推算(DR)组合定位的基础上,先引入当前统计模型进行分析,随后采用卡尔曼对GPS和航位推算(DR)的定位信息进行跟踪滤波,最后采用Matlab软件对HADDB型现代有轨电车在某不同半径弯道的定位情况进行仿真。
1 GPS与DR组合定位
1.1 DR
DR就是将车辆传感器的测量值转换成估计位置的定位技术,可以基于车辆的最近位置(ai-1,bi-1),结合里程计和数字罗盘的信息来估计移动车辆的当前位置(ai,bi),其原理图如图1所示。里程计可获取行进距离,数字罗盘是由磁力计改进的电子设备,可获取车辆与地磁北极间的角度(即方位角θ)。经典的DR方法会在局部坐标系中用到三角函数,它的解为[6]:

(1)
式中:
θi-1——(ai-1,bi-1)处的车辆方位角;
θi——(ai,bi)处的车辆方位角;
Δsi-1——(ai-1,bi-1)与(ai,bi)的距离。

图1 DR原理示意图
1.2 组合定位
GPS与DR组合定位常用互换式结构和融合式结构,如图2~3所示。
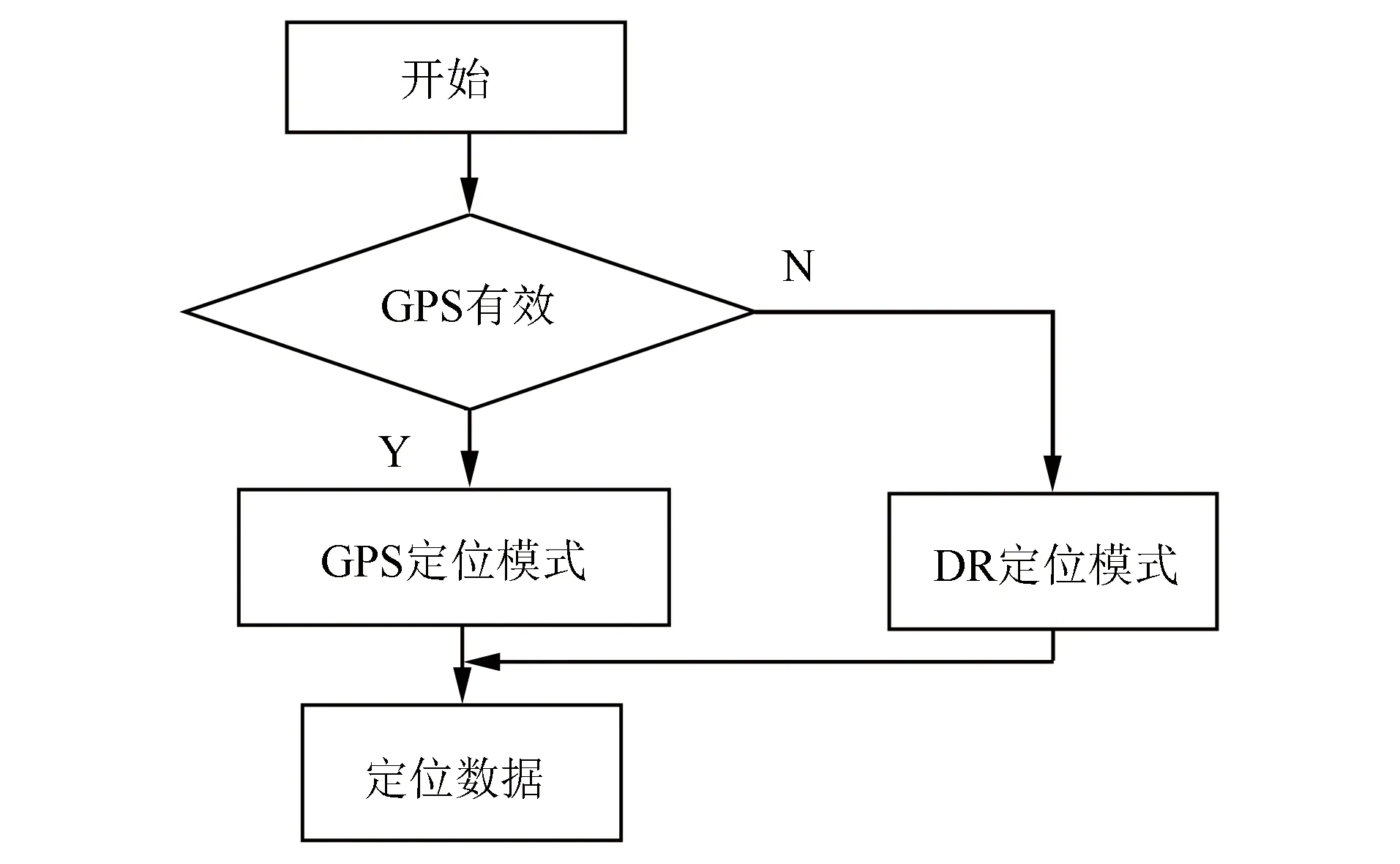
图2 互换式组合定位框图
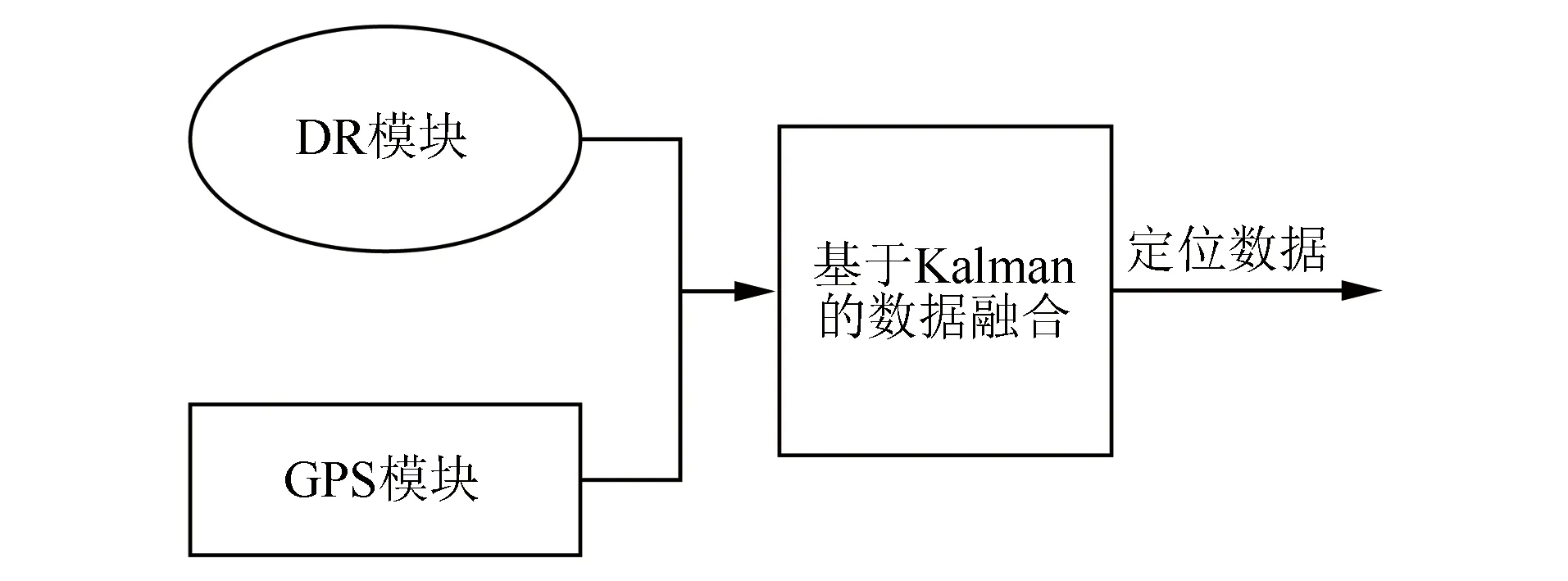
图3 融合式组合定位框图
在互换式结构中,如果没有受到线路沿途干扰,且GPS能够正常工作,则为GPS定位模式,单纯地依靠GPS输出定位数据;如GPS处于定位盲点,则自动切换为DR定位模式,依赖DR输出定位信息。互换式结构的优点在于算法简单,可实现程度高,但是该结构没用充分利用多传感器的信息来提高定位的准确性,运用于实际定位中的意义不大。
融合式结构的工作机制不变,将GPS模块和DR模块的数据采集信息同时传入卡尔曼滤波器中,进行数据融合后输出详细的定位结果。融合式结构不需要再特别判定GPS工作状态是否正常,就能实现统计最优估计,从而降低定位误差,显著提高定位精度。本文选择融合式组合定位。
2 运动模型仿真分析
2.1 建立运动模型
在跟踪目标的过程中,目标不可能一直做匀速或匀加速运动,而随时会出现转弯或紧急制动等运动。这种很随意的运动称为机动[7]。常见的机动目标有Singer模型及当前统计模型等。
Singer模型利用系统模型的噪声方差和状态转移矩阵来处理有色噪声,并得到相关系统参数。但是该模型不能很好地描述所有实际机动目标的运动。
当前统计模型的本质是非零均值时间相关模型。当前统计模型将机动模型和滤波过程形成了闭环结构,可根据滤波结果实时调整系统模型。
当前加速度由概率密度修正的瑞利分布来描述,均值为当前加速度预测值。随机加速度在时间轴上符合一阶时间相关过程[8]:

(2)

(3)
式中:
ar(t)——机动加速度均值,在每个采样周期内为常数;
a(t)——零均值的有色噪声;
x(t)——列车在t时的位置;
α——机动加速度时间常数的倒数;
ωc(t)——均值为零的白噪声。
若令当前机动加速度ac(t)=ar(t)+a(t)并代入式(2)和式(3)中,可以得到:

(4)

(5)
则当前统计模型的数学表达式为:


(6)
即:
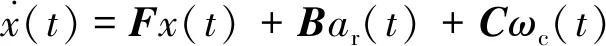
(7)
其中,

(8)
经过积分得到动力学模型为:
x(k+1)=Ax(k)+Uar(t)+ω(k)
(9)
其中,

(10)

(11)
噪声ω(k)的方差为Q

(12)
式中:
k——迭代次数;
q——常数矩阵元素;
T0——采样周期。
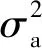

(13)
式中:
aM——为最大加速度。
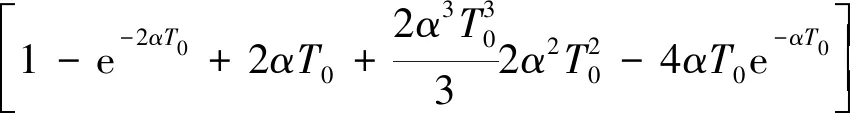
(14)

(15)

(16)
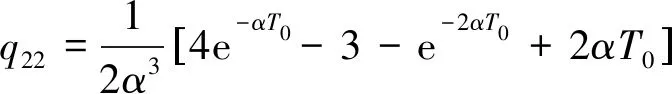
(17)

(18)
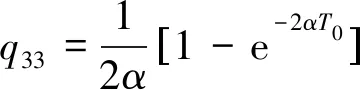
(19)
2.2 算法
首先,同时对GPS和DR数据进行采集;随后,将两部分的数据输入当前统计模型中,输入包括采样周期、当前的状态估计值、机动频率等,输出式(10)~(13);之后,经当前统计模型处理过的数据再利用卡尔曼进行滤波;最终,得到详细的定位数据。其中,卡尔曼滤波的状态方程式为:
x(k+1)=Ax(k)+V(k)
(20)
其中矩阵A同式(9),且有
V(k)=Uar(t)+ω(k)
(21)

(22)

(23)
式中:
ZD——加速度观测方程;
VD——加速度测量噪声;
ZG——速度观测方程;
VG——速度测量噪声。
最后对定位数据进行误差估计并输出。
2.3 仿真试验
本文使用Matlab软件,选取淮安现代有轨电车1号线一期下行线路中具有代表性的小半径(R=40 m)、中等半径(R=400 m)、大半径(R=800 m)曲线分别进行仿真。仿真采用蒙特卡罗(Monte Carlo)法。其中,执行程序的次数N=500,采样间隔t=0.01 s,机动频率i=1/100。
小半径曲线的各项仿真结果如图4~6所示。图6中x轴估计误差绝对值最大处的坐标为(2.950,2.002),y轴估计误差绝对值最大处的坐标为(0.820,2.555)。因此,小半径曲线定位的误差不大于3.246 m。

图4 小半径曲线仿真轨迹对比
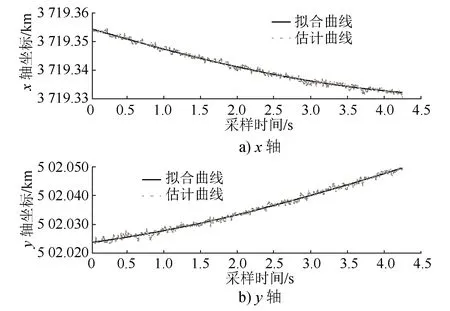
图5 小半径曲线横纵轴坐标估计结果

图6 小半径曲线横纵轴坐标估计误差
中等半径曲线仿真结果如图7~9所示。特别地,图9中x轴估计误差绝对值最大处的坐标为(1.820,-2.561),y轴估计误差绝对值最大处的坐标为(1.340,-1.907)。所以,中等半径曲线定位的误差不大于3.193 m。
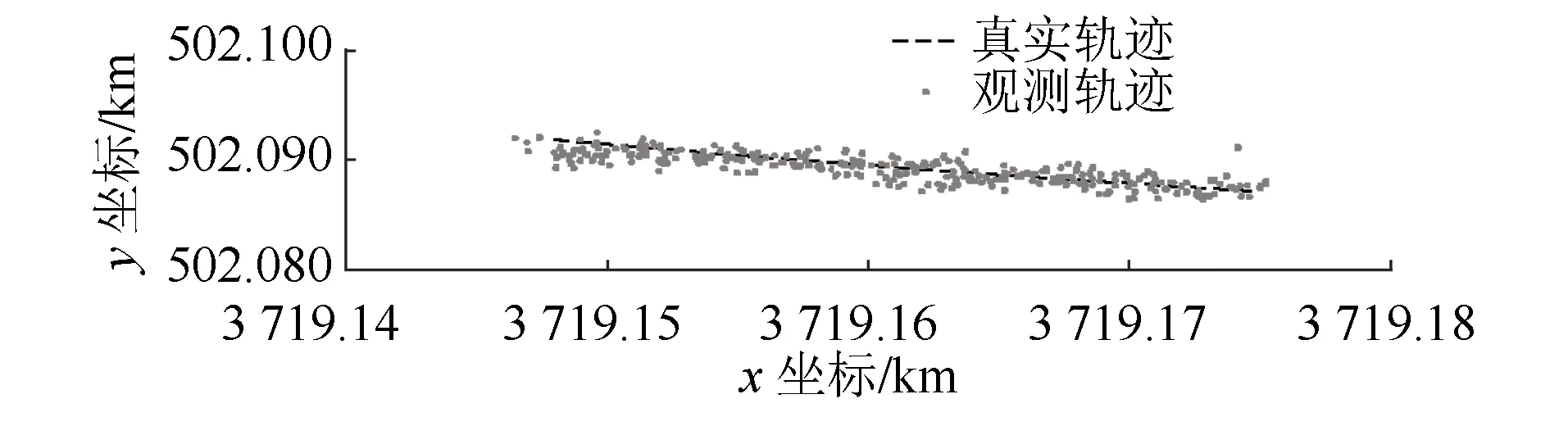
图7 中等半径曲线仿真轨迹对比

图8 中等半径曲线横纵轴坐标估计结果

图9 中等半径曲线横纵轴坐标估计误差
图10~12为大半径曲线仿真结果。不难看出:图11中x轴估计误差绝对值最大处的坐标为(0.440,-1.927),y轴估计误差绝对值最大处的坐标为(2.210,-2.421)。由此可得,大半径曲线定位误差不大于3.094 m。

图10 大半径弯道仿真轨迹对比
综上所述,基于淮安现代有轨电车1号线各半径弯道的定位仿真误差最大为3.246 m,根据文献[10],属于第二类误差。根据文献[5],使用Singer模型时的最大误差为5.8 m[5]。由此可见,基于当前统计模型的GPS与DR组合定位精度优于基于Singer模型的组合定位精度。

图11 大半径曲线横纵轴坐标估计结果

图12 大半径曲线横纵轴坐标估计误差
3 结论
本文以现代有轨电车为研究对象,针对有轨电车的组合定位进行了深入研究。基于有轨电车高精度定位的目标,提出了当前统计模型与卡尔曼跟踪滤波结合的GPS/DR定位方案,并进行了仿真试验。
仿真结果表明,新的模型分析方法能大幅降低定位误差,可以在短时间内输出可靠的定位信息,能满足有轨电车连续高精度的定位需求。
