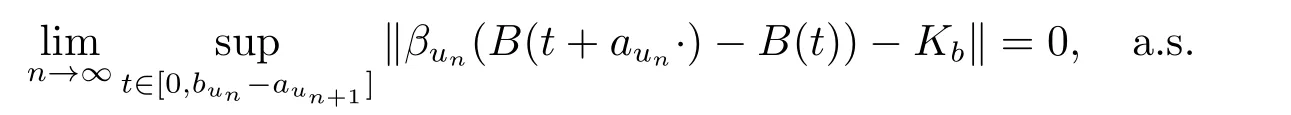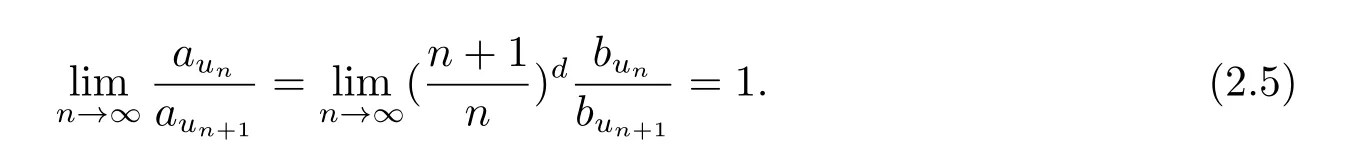Brown运动增量局部重对数律的一个注记

莫永向

(桂林电子科技大学数学与计算科学学院,广西高校数据分析与计算重点实验室,广西 桂林541004)

1.引言与主要结果

设{B(t);t≥0} 是d维标准Brown运动.C0[0,1]={f;f:[0,1]→Rd,f(0)=0,f连续}赋予一致范数‖f‖=sup lim0≤t≤1|f(t)|.设au,bu是两个从(0,1) 到(0,e−1)非减连续函数,且满足

(i) 0≤au≤bu,u∈(0,1)并且

定义映射I:C0→[0,∞]如下

记Kb={f∈C0[0,1],2I(f)≤b2},其中

对u∈(0,1),0≤t≤1,记∆(t,u) 为下面轨道:

设

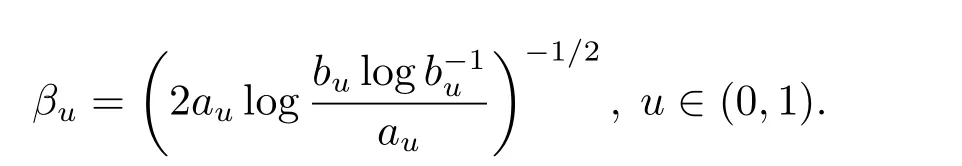
本文的主要结果如下:

定理1.1如果条件(i),(ii)和(iii)成立,那么以概率1,{βu∆(t,u);u∈(0,1)}(u→0)在C0中相对紧,且其极限点集是Kb.即,

且

注1.1定理1.1的条件(iii)中r=∞即时,见文[5]的定理1.1.

推论1.1记Mt,h(x)=0≤x≤1,0≤t≤1−h,我们有

且

Brown运动及其增量的极限定理是一个广泛研究的课题,已有许多成果.GAO等[1]研究了一致范数下Brown运动增量的泛函极限及其收敛速率.危启才在[3]中得到了k维布朗运动C-R型增量在Hölder 范数下的泛函极限定理.对Brown运动局部极限定理人们也有研究,危启才在文[4]中研究了Brown运动在Hölder范数下的泛函连续模.GAO等在文[5]中研究了一致范数下Brown运动增量的局部的泛函极限及其收敛速率.对0

2.定理的证明

定理的证明需要下面的Schilder大偏差.

引理2.1[2]对任何Borel集A⊂C0,

其中Λ(A)=inff∈A I(f).

定理1.1的证明当r=0时,b=0,Kb={0},显然成立.因此,我们只需考虑0

由于01 且非减,故存在ρ∈[0,1],使得

若0<ρ≤1,则又由条件(i):知否则,与矛盾.于是,即r=0,此时,显然成立.

所以,ρ=0,即,从而

证(1.1)式,我们首先证,存在一个趋于零的非增数列un,使得

记A1={f∈H:‖f−Kb‖≥ε}.显然,A1是闭集,Λ(A1)故存在充分小δ >0,使Λ(A1)+δ.

记η:=δ−+rσ+δσ,则η >δ−δ(1+r)+rσ+δσ=rσ+δσ >0.取一个趋于零的非增数列un,使得bun=e−en,对任意小的ε>0,由(2.2)式和引理2.1,当n充分大时,我们有

由于

故(1.1)式成立.

再证(1.2)式.记ψt,u(s)=βu(B(t+aus)−B(t)),s∈[0,1],t∈[0,bu−au],则

由(2.1)式:limu→0+=∞,故可取一个趋于零的非增数列un,使得其中0

先估计I1.令kn=因为2 infg∈A2I(g)0,使得2 infg∈A2I(g)

令h(n)=那么h(n)单调非减,=r >0且又注意到0

于是,

又因为βu和log非增(u∈(0,e−1)),所以

又由于

并结合(2.6)式,我们又有

由(2.3),(2.4),(2.7)和(2.8)式知(1.2)式成立,定理1.1证毕.