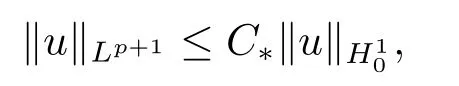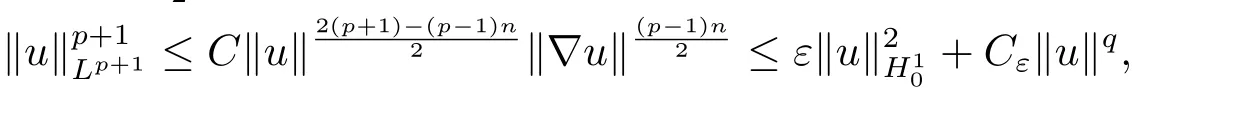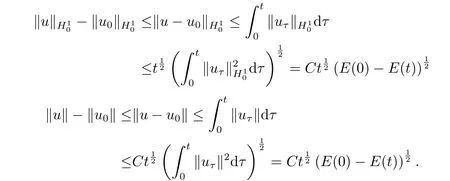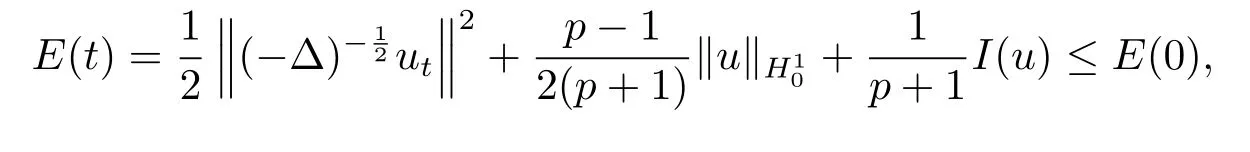耗散Boussinesq方程弱解的爆破
2019-10-16苏晓王书彬宋瑞丽
苏晓,王书彬,宋瑞丽
(1.河南工业大学理学院,河南 郑州450001;2.郑州大学数学与统计学院,河南 郑州450001;3.中原工学院信息商务学院,河南 郑州450007)
1.引言
本文研究下列初边值问题

的弱解在有限时间发生爆破的充分必要条件及爆破时间的下界估计,其中Ω是Rn中具有光滑边界的有界区域,∂Ω是Ω的边界,f(u)=|u|p−1u,1
−βλ1,λ1>0是−∆在Dirichlet边界条件下的第一特征值,下标t表示对t的偏导数.
1872年Boussinesq[1]提出一类描述浅水长波的方程

并给出了方程(1.4)的某些特殊孤立波.1974年Zakharov[13]提出方程(1.4)的另一种形式

用来描述非线性弦振动.方程(1.4)和(1.5)被后人称为Boussinesq(Bq)方程.Bq方程的提出第一次对Russel提出的孤立波现象[8]做出了科学的满意的解释[2].Bq方程是经典线性波方程的扰动形式,结合了非线性和色散的基本思想,这也是许多水波模型的特点.此后Bq方程得到了广泛的研究应用和推广,从不同形式的非线性项的角度出发提出了广义Bq方程

Bq方程及其广义形式的定解问题得到了广泛的研究,并取得了丰富的研究结果,这些结果主要集中在初值问题和初边值问题弱解和强解的整体适定性、有限时间爆破及解的长时间行为.1988年Bona和Sachs[2]研究了方程(1.6)的初值问题.作者使用拟线性发展方程的Kato理论证明了问题的局部适定性,并进一步证明了古典解的存在性.1993年Linares[4]研究了方程(1.6)的初值问题,其中非线性项为f(u)=|u|αu.通过建立相应的线性问题解的光滑效应(Lp-Lq估计或Strichartz 估计)结合压缩映像原理讨论了低正则局部解,通过建立能量等式进一步证明了当初值分小时H1(R)中的局部解可延拓为整体解,并给出了解的衰减性质.1995年LIU[5]利用凸性方法证明了方程(1.6)孤立波解的不稳定性.2000年LIU[6]研究了当初值落在基态解的某个小邻域内时解的有限时间爆破,此结论是文[5]中爆破结果的一个改进.
Bq方程及广义Bq方程孤立波的存在性说明了非线性项和色散之间的平衡.在耗散系统中没有能量守恒而是能量生成(energy production) 和耗散之间的平衡关系.为了描述非线性项、能量生成和耗散之间的关系,1994年Christov和Velarde[3]提出了用来描述薄粘性液体中流动的耗散Bq方程:

方程(1.7)还可描述非线性弹性梁的振动[9].当α4=0时,方程(1.7)就是阻尼Bq方程.
WANG和SU在文[11-12]中分别研究了方程(1.7)的初边值问题和初值问题,讨论了在三种不同初始能量状态下弱解的整体适定性及弱解在有限时间爆破的充分条件,并在文[12]中讨论了低初始能量状态下解在有限时间发生爆破的必要条件.其中在文[11]中得到了如下结论:若存在时间t0使得u(t0)落在位势井集合,

内,则存在时间Tmax使得问题(1.1)-(1.3)的弱解u满足
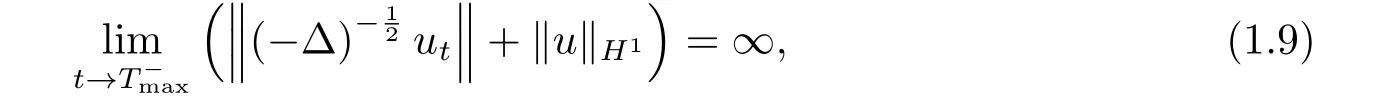
其中

I(u)也被称为Nehari泛函,位势井深度d定义为

关于位势井深度的讨论可以参看文[5,7,10].反之,若问题(1.1)-(1.3)的弱解满足(1.9),是否一定存在时间t0≥0使得u(t0)∈V?本文将证明在非线性增长阶p满足一定条件下,上述结论是正确的,即给出了问题(1.1)-(1.3)的弱解在有限时间爆破的必要条件.此外本文还给出解存在的最大时间Tmax的一个下界估计,这些结论在文[11]中未得到讨论,本文是对文[11]的一个补充说明.
文中将使用标准的符号:Lp=Lp(Ω)表示Lebesgue空间,‖· ‖Lp表示Lp中的范数,其中1≤p≤∞,为了书写方便,用‖· ‖表示L2中的范数;H10=H10(Ω)表示Sobolev空间,‖·‖L2+‖∇·‖L2与‖∇·‖L2是H10中的等价范数;(·,·)表示L2中的内积.
2.预备知识
文[11]中给出了问题(1.1)-(1.3)的局部适定性并建立了能量等式.
定理2.1令p满足

则存在时间Tmax>0,使得问题(1.1)-(1.3)有唯一弱解u满足

且
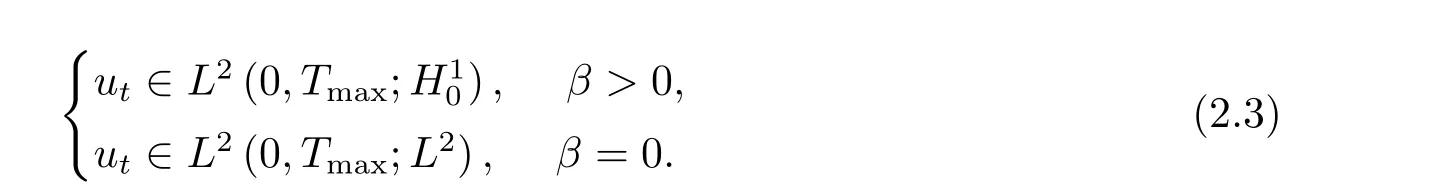
进一步有能量守恒式成立,即

其中

另外,如果

则Tmax=∞.
定义2.1如果Tmax<∞,则称问题(1.1)-(1.3)的弱解在有限时间爆破,Tmax称为爆破时间;如果Tmax=∞,则称问题(1.1)-(1.3) 的弱解是整体存在的.
3.主要结论及证明
定理3.1令p满足(2.1) 且当β=0,1≤n≤4时1 注3.1假设条件:β=0,1≤n≤4时p满足1 证充分性的证明参看文[11]中定理2.6. 下面给出必要性的证明. 步1 我们首先证明若Tmax<∞,则有 特别地,当β=0时有 事实上,若Tmax<∞,由定理2.1可知 由能量守恒式(2.4)可得 由此可知 由p的假设条件可知H10+1,故 其中C∗是Sobolev最佳嵌入常数,则(3.1)成立. 当β=0时,注意到则由Gagliado-Nirenber不等式和ε-Young不等式可知 取ε<1,由(3.1)可得(3.2). 步2 证明 注意到 则由Hölder不等式和能量等式(2.4) 可得 对以上两个不等式两边取极限,令,并由(3.1)和(3.2)知(3.4)成立. 由E(t)和I(u)之间的关系式, 可知 故一定存在t0∈[0,Tmax)使得 定理2.1得证. 定理3.2令p满足(2.1).如果问题(1.1)-(1.3)的弱解在有限时刻Tmax发生爆破,则 当β >0时 当β=0时 证令 则由能量等式(2.4)可知 上式两边关于t求导可得 下面我们分β >0和β=0两种情况分别讨论. 情形1当β >0时,由假设条件(2.1),并使用Hölder不等式和Sobolev嵌入定理可得 由插值不等式可知 当0<θ <1时,上式可化简为 其中b=(C1Cp∗cθ∗)2,a=1−θ.解此常微分不等式得 当θ=1,即n≥3且p=时H(t)可估计为 解得 (3.9)和(3.10)说明H(t)至少在[0,T)上是有界的,其中T由(3.5)定义. 情形2当β=0时,由条件(2.1)和Young不等式,可知 将上式带入(3.7) 可得 这个式子说明H(t)至少在[0,T)上是有界的,其中T由(3.6)定义.定理得证.