轴承试验机液压缸薄膜材料对加载误差的影响

2019-10-16汪卫兵吕赛赛高奋武李智刚

西安科技大学学报 2019年5期

汪卫兵，吕赛赛，高奋武，李智刚，赵宽

(1.西安科技大学机械工程学院，陕西西安 710054；2.洛阳轴承研究所有限公司，河南洛阳 471000)

0 引言

在轴承试验机中，为了模拟轴承的实际受载情况，要对被试轴承施加一定的轴向载荷和径向载荷[1]。轴承试验机常用加载方式有杠杆砝码加载、弹簧加载、静液压加载、液压比例自动加载、液压伺服加载等[2]。液压比例加载系统凭借其成本适中，控制精度高，载荷可控等优点，在轴承试验机中被大量使用[3]。目前常用的轴承试验机加载液压缸的压力可达0.5～6 MPa，一般不超过10 MPa[4]，传统液压缸结构无法达到很好的密封和加压效果，而液压缸作为液压加载系统的关键作用部件，其性能对整个液压加载系统的加载效果显得尤为重要。

在轴承试验机的实际使用中，发现液压缸活塞实际输出载荷F实与控制器中的设定载荷F试相比存在一定的误差[5]。针对这个问题，国内外学者对提高轴承试验机的试验精度、可信度以及液压加载系统的加载精度进行了大量研究。李兰杰等人采用伺服电动缸来取代传统的纯液压伺服加载方式，开发了基于PID控制算法为核心的全闭环控制算法，提高了系统加载精度[6]。付曙光等研究了摩擦力对伺服液压缸加载精度影响的机理，并开发了相关的测试试验软件[7]。郜立焕等研究了闭环控制电路对步进液压缸精度的影响，通过线性系统分析方法得出了其加载的精度指标[8]。贾善斌等主要研究了PID控制、模糊控制的控制方式对多级液压缸同步精度的影响，其研究表明模糊-PID控制算法能够较好地满足此液压系统的同步精度和稳定性要求[9]。黄杰等人研究了伺服电动缸加载系统中机械结构的摩擦、间隙等非线性因素对加载精度造成的影响，并基于三阶电动缸压力系统的力闭环自抗扰控制器实现了系统抗干扰能力强加载精度高的效果[10]。Xie Ning等利用遗传算法，优化可影响液压缸位置精度的PID参数，优化后的参数可以明显提高系统的加载精度[11]。Su Dong Hai等人在详细分析PID控制响应状态的基础上，采用模糊控制技术和表格模糊PID控制算法来满足液压加载系统的控制精度[12]。MaoHsiung Chiang等人开发了一种H-控制用于解决双输入单输出控制系统，此系统中伺服液压缸用于粗略定位，压电致动器用于精细控制。液压压电混合定位伺服系统可以在180 mm行程和约15 kg负载质量下达到约0.1 mm的精度[13]。Junbo Lei研究了额定流量对活塞位置精度的影响，并提出了新的系统结构及其控制方法，能够满足预期的活塞位置精度控制要求[14]。Jun Xiao等人研究了一种用于驱动具有多种速度选项的液压差速器气缸的液压控制模式，通过调节泵的速度和方向，使用2个不同的泵来控制油室两侧的气缸来达到精确控制的目标[15]。XiuXu Zhao等人基于液压缸泄漏故障机理，提出了一种基于位移信号和压力信号融合的液压缸故障诊断方法[16]。Hongjie Li等人提出了一种模糊PID控制器，解决了双向液压缸协同运动过程中产生的交叉耦合误差，可以在复杂恶劣的条件下实现较高的位置精度控制[17]。

通过分析液压缸的具体结构和工作原理，初步认为加载误差的来源可能有以下几个方面：①薄膜变形产生的弹性阻力；②薄膜存在一定的边缘效应导致薄膜不能很好的贴合活塞端面；③液压缸活塞端面面积小于理论面积；④活塞与液压缸壁存在摩擦力等[18]。文中根据薄膜液压缸薄膜的受力情况，通过实验比较了不同的薄膜材料对液压缸加载误差的影响，从而提出了一种改进液压缸装配参数的误差修正方法，有效提高了液压缸的加载精度。

1 液压缸加载误差的产生原因

1.1 液压缸工作原理

液压加载是轴承试验机主要采用的加载方式之一[19]。由液压泵输出的压力油经单向阀、滤油器，通过溢流阀，按工作需要调整压力后，进入比例减压阀，比例减压阀在控制器的作用下连续输出预先设定压力的液压油，推动隔膜通过活塞向试验轴承施加载荷[20]。活塞输出的载荷大小F试等于液压缸内液压油的压强P乘以活塞端面的作用面积S，该载荷是一种等效载荷，其计算公式为

F试=P·S

(1)

液压缸具体结构如图1所示。

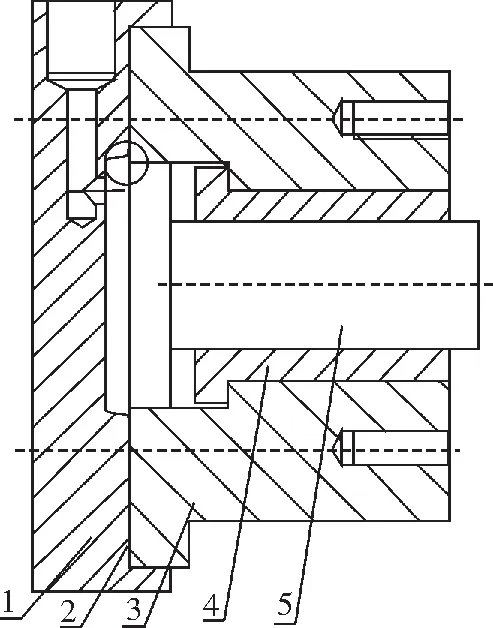
图1 液压缸结构Fig.1 Structure of film cylinder1 缸盖 2 薄膜 3 液压缸 4 套筒 5 活塞

轴承试验机加载时通过计算机向控制器发送指令，控制比例减压阀输出一定压强的液压油，液压缸中的实际油压P实由液压缸内的压力传感器测得，并向控制器传送电信号，控制器接收此反馈电信号与设定的压强值进行比较，再由控制器对比例减压阀的实际输出油压P实进行调节，形成加载系统的闭环控制，实现加载系统的精确、自动加载[21]。

图2 放大的液压缸加载边界变形Fig.2 Enlarged loading boundary deformation of film cylinder 1 液压油 2 薄膜 3 活塞

1.2 液压缸误差产生原因

在上述试验机加载过程中，在设定载荷情况下液压缸中的液压油以压强P试作用于薄膜，使薄膜通过活塞杆向被试轴承施加载荷。但是在实际结构中，为了防止活塞头边缘对薄膜的剪切作用过快损坏薄膜，以及便于装配的工艺要求，通常将活塞端面的边缘设计为R0.5-R1的圆角。同时由于薄膜变形时存在边缘效应导致薄膜发生硬化现象[22]，导致薄膜与活塞端面边缘不能良好的贴合，如图2所示，这就造成了薄膜作用的活塞端面面积小于活塞端面的实际面积，导致F实与F试不一致。与此同时，由于压力油作用在薄膜上，导致薄膜发生弹性变形，给加载系统增加了额外的弹性阻力F弹。因此，在上述几种因素的作用下会导致轴承试验机实际加载值与额定值出现偏差。加载误差的存在直接影响了轴承试验数据的准确性，使得试验数据难以真正的反映出被测试轴承的真实性能指标。因此，找到误差产生的原因并将误差缩小到允许的范围内就显得至关重要。

2 液压缸等效载荷误差实验

2.1 不同材料液压缸加载的有限元分析

为了研究上述薄膜零件对轴承试验机加载误差的影响规律，采用有限元数值模拟实验分析薄膜材料对液压缸加载精度的影响。试验选取目前液压缸中常用的3种薄膜材料：氟橡胶、聚四氟乙烯和丁晴橡胶，厚度均为1 mm，3种材料的部分性能参数见表1.

表1 3种薄膜材料性能参数

3种薄膜材料都属于超弹性材料，根据其在液压缸中的实际工况，其本构模型选用Mooney-Rivilin模型[23]，其本构方程如式(2)所示。液压缸缸体和活塞采用45钢，其弹性模量为210 GPa，泊松比分别为0.3.

(2)

对于完全多项式如果N=1，只有线性部分的应变能保留下来，就是Mooney-Rivilin模型，如式(3)所示。通过计算可以得到3种材料的材料系数C01，C10见表2[24].

(3)

利用有限元分析软件Abaqus建立薄膜受载的二维简化模型，如图3所示。通过向薄膜施加压强载荷P后测试受载件受到的活塞杆的接触压力F，计算加载误差比W，得出不同加载情况下的误差比变化趋势图，如图4所示。

图3 液压缸加载有限元简化模型Fig.3 Simplified model of thin-film cylinder loading finite element 1 薄膜 2 缸体 3 活塞 4 受载件

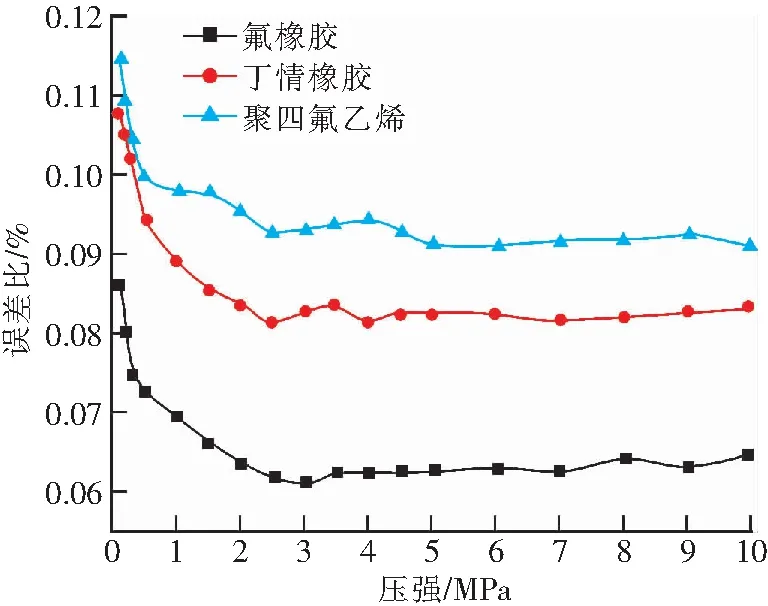
图4 不同薄膜材料的数值模拟实验加载误差比Fig.4 Numerical simulation experiment loading error ratio of different film materials

从图4可以看出，开始加载时由于载荷较小，受到的阻力，如薄膜的弹性阻力、接触面间的摩擦力等因素的影响相对较大，所以3种材料的误差比都很大。随着载荷不断增大，3种材料的误差比都明显减小。并最终逐渐稳定在一定的范围内。3种薄膜材料中，氟橡胶由于其良好的变形性能，产生的弹性阻力最小，因此误差比最小，最终误差比稳定在6.4%左右；丁晴橡胶性能次之，误差比稳定在8.2%左右；聚四氟乙烯材料性能最差，所以误差比最大，稳定状态下达到了9.1%左右。

2.2 不同材料液压缸的物理加载实验

为了对数值模拟实验得到的结果进行验证，本研究设计并进行了一种加载测试试验。试验采用一种轴承试验机加载测试装置，其核心工作部件简化结构如图5所示。试验时将本装置固定在轴承试验机底座上，在液压缸活塞与测试定位块中间设置一个经过校核、误差在允许范围内(满量程稳态误差0.2%FS)的测试力传感器，试验所用薄膜材料与有限元数值模拟实验所选材料相同，为氟橡胶、聚四氟乙烯和丁晴橡胶3种，厚度选用目前液压缸薄膜零件常用尺寸1 mm.

试验中通过加载系统向液压缸中逐渐加压，通过液压缸内压力传感器记录油压P实的变化，并通过加载测试装置的测试力传感器采集被测物体的受力情况F实，然后根据计算出来的额定载荷F试与测试定位块上的力传感器采集到的实际载荷F实数据计算出不同材料、不同载荷情况下的误差比W，得出加载误差比的变化关系。具体计算公式为

(4)

式中W为误差比；P实为液压缸内压力传感器测得的油压，MPa；S为活塞端面面积,mm2；F实是测试力传感器测得的被测物体的受力,N.

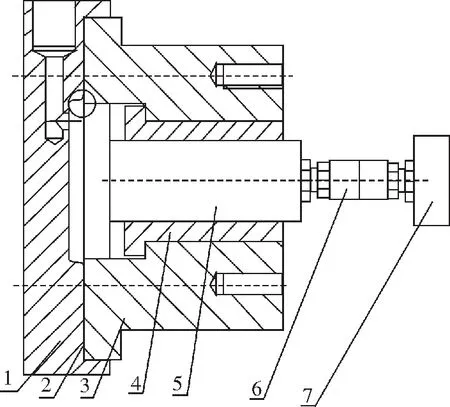
图5 轴承试验机加载辅助测试装置示意图Fig.5 Bearing test machine loading auxiliary test device1 缸盖 2 薄膜 3 液压缸 4 套筒 5 活塞 6 力传感器 7 测试定位块

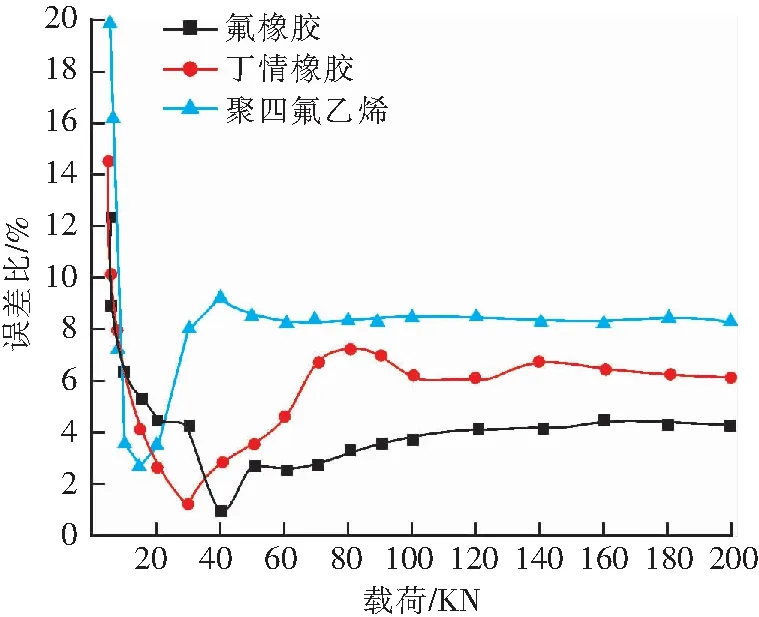
图6 不同薄膜材料的加载误差比Fig.6 Load error ratio of different film materials

图6为加载试验所得结果，从图中可以看出，与数值模拟实验的理想加载情况不同，实际加载中，由于载荷波动，在最开始加载时系统误差比很不稳定，处于较大的波动状态，这种波动受活塞与缸壁摩擦力，薄膜边缘效应、弹性阻力等因素的综合作用，由于此时施加载荷较小，上述干扰因素影响较大，所以误差比波动很大。随着载荷不断增加，3种薄膜材料最终稳态误差的误差比稳定在一定的范围内。3种薄膜材料中，氟橡胶由于其良好的变形性能，产生的弹性阻力最小，因此误差比最小，在4.6%左右；丁晴橡胶次之，误差比在6.9%左右；聚四氟乙烯材料性能最差，所以误差比最大，达到了8.5%左右。

对比2种实验得出的结果可以看出，加载过程中，由于数字模拟试验的材料性能、加载效果等条件较为理想稳定，因此载荷误差比波动较小，随着载荷的增大，误差比逐渐减小，并最终稳定在一定范围。实际加载误差由于载荷处在一定的波动下，并受多种干扰因素的影响，加载最初的误差比很不稳定，但是经过一段时间加载后，误差比最终稳定在一个范围内。2种实验的结果的变化趋势较为吻合。

2.3 加载误差改进方法

考虑到薄膜边缘效应对液压缸加载造成的影响，提出了一种改进思路，即装配时预先将活塞杆端面安装位置高出液压缸缸体端面一段距离，克服活塞端面倒角造成的薄膜不能完全贴合的情况，从而减小误差，其效果如图7所示。

为了验证上述思路，在有限元模拟实验中，将活塞杆装配位置依次调整为高出液压缸端面x=0.1,0.2,0.3,0.5 mm，选用氟橡胶薄膜材料进行对比试验，对比了调整前后的误差比变化，具体结果如图8所示。

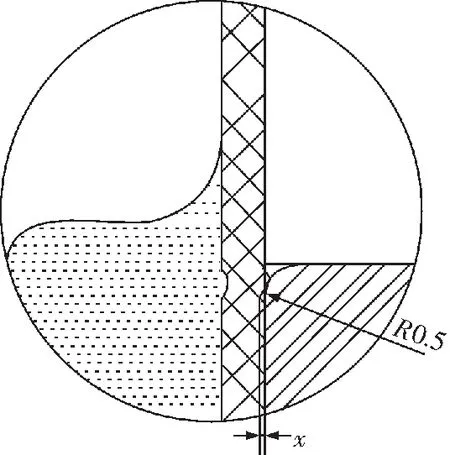
图7 调整后的液压缸加载边界变形效果Fig.7 Adjusted deformation of the film cylinder loading boundary

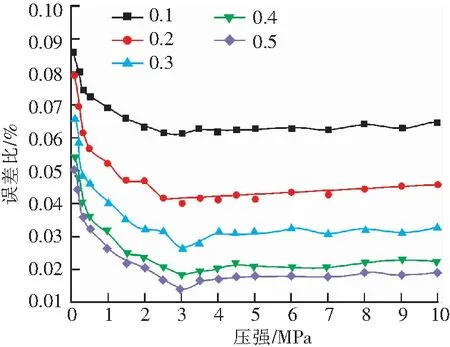
图8 调整后的氟橡胶薄膜的加载误差比变化Fig.8 Change of loading error ratio of adjusted fluororubber film

从试验结果可以看出，调整前氟橡胶最终稳态误差比为6.4%左右，调整为高出液压缸端面0.1，0.2，0.3，0.5 mm时，最终稳态误差比依次为4.4%，3.2%，2.5%，1.9%左右。可见，经过上述方式调整后，误差比明显要比调整前降低。且相对于未调整状态，调整后普遍能更快达到误差比较稳定的状态。且在调整为高出液压缸端面0.5 mm时，最终稳态误差比已经低于2%，满足轴承试验机试验精度的需要。因此该方法对于降低由于边缘效应带来的误差有效，且此方法操作简便，节约时间与成本。在实际使用中，应根据不同的液压缸型号，加载压力范围以及薄膜材料等因素，经试验得出需要调整的值。