煤层冲击倾向性评价的新指标体系

吴学明，王苏健，张天军，黄耀光，黄克军

(1.陕西煤业化工技术研究院，陕西 西安 710065；2.煤炭绿色安全高效开采国家地方联合工程研究中心，陕西 西安 710065；3.西安科技大学 理学院，陕西 西安 710054)

0 引 言

冲击倾向性是煤层的固有力学属性，它是关于能量和时间的函数[1]。基于损伤统计本构模型的冲击倾向性评价是评价、预测及防治冲击矿压的理论基础[2-4]。针对煤层冲击倾向性指标包括弹性能指数、冲击能指数、动态破坏时间、单轴抗压强度等[5]，其分别从能量、时间和承载能力的角度对煤层冲击倾向性进行评价。苏承东、蔡武根据现场实践和室内实验分析了上述指标间的相关性[3,6]，且蔡武等提出了最大损伤速率和反应动态破坏时间的动态损伤应变新指标[3]。此外，郭建卿、唐礼忠提出有效冲击能指数、单轴抗压强度与单轴抗拉强度之比、峰值前后应变量之比等指标[7-8]，并指出有效冲击能指标更能反映煤样在压缩变形破坏过程吸收和释放能量的关系[8]；潘一山提出用冲击能量指数除以动态破坏时间得到冲击能量速度指标[9]，解决了冲击倾向性判别结果误差大、离散性等难题；唐礼忠提出剩余能量的概念及以剩余能与峰后破坏耗散应变能的比值作为剩余能量指数指标[10]；姚精明从宏细观能量耗散的角度出发提出弹性应变能衰减度和塑性变化率指标[11-12]，基于此的分级指标更贴近工程实际。以上研究极大地丰富了冲击倾向性指标体系，但均从实验曲线出发来直接制定评价指标，并且存在受实验加载方式的限制，指标计算不便，评价结果误差较大等问题。而吴政提出的损伤统计本构模型对未考虑残余强度的应力—应变曲线拟合度较高，且曲线上不同特征点处的损伤规律简洁、明了，但该模型未能体现出煤体存在残余强度的这一事实[13]；杨圣奇利用损伤比例系数得到了可反映残余强度的损伤统计本构模型，为煤岩冲击倾向性的评价提供了新思路[14]；蔡武由此引进动态损伤应变和最大损伤速率指标来评价冲击倾向性，但其动态损伤应变的力学意义不明确，且未得到最大损伤速率理论解，致其应用不便[15]。

基于以上研究中的不足，文中建立考虑残余强度的损伤统计本构模型，研究了峰值点、损伤速率最大值点、损伤加速度最值点处的损伤规律，得到损伤速率最大值表达式，并讨论了模型中各参数的物理意义。继而对残余强度和动态损伤应变进行修正，提出新的评价煤岩冲击倾向性指标—盈余能指数变化率，并构建新的冲击倾向性指标体系，最后利用冲击倾向性实验对上述指标体系的合理性进行验证。

1 损伤统计本构模型及特征点

1.1 损伤统计本构模型

根据煤岩微元强度服从韦伯分布的假设[16]和连续介质损伤力学理论[17]，采用能够反映煤岩材料弹性、塑性及残余强度的单轴压缩条件下考虑残余强度的煤岩损伤统计本构模型为

(1)

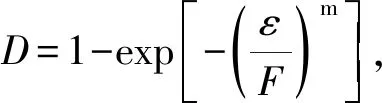
m=

(2)

而该模型中，cn为损伤比例系数，其煤岩在残余强度的取值范围(0，1)，为无量纲常量，其主要用于描述应力应变曲线残余强度特点而引进，需预先设定。除此外，上述参数还可用最小二乘法对实验数据进行参数拟合得到[18]，进而与上述理论结果进行对比验证。

1.2 特征点分析

损伤速率为描述煤层损伤积累快慢的物理量，通常由损伤因子对应变求一阶导得到，即

(3)

因实验过程中采用按位移加载的方式，故应变对时间导数dε/dt为定值，则式(3)即可描述损伤随时间积累的快慢。

为了更加方便的研究损伤速率的变化规律及损伤速率的最大值，提出损伤加速度概念，可由损伤因子对应变求二阶导得到，即

(4)

当cn=0.98，m=4，F=0.02，E=3 000，研究峰值强度点A(图1)，损伤速率最大值点B、损伤加速度最大值点C和损伤加速度最小值点D的应力应变及损伤情况(图2)。

A点是指应力-应变曲线的峰值强度点，此处应力达到最大值，其坐标为A(εmax,σmax)。已知峰前弹性应变与峰值强度点应变关系为

εth=εmax/E

(5)

式中εth为峰前弹性应变；εmax为峰值点处的应变;E为材料的无损弹性模量。如图1所示，此时的损伤因子约为20%，即当材料处于峰值强度时的损伤比例维持在较低水平。

B点是指损伤速率曲线的峰值点，其坐标为B(εB，DB)，对应的损伤加速度为零，如图2所示。令损伤加速度表达式(4)等于零，可得

(6)

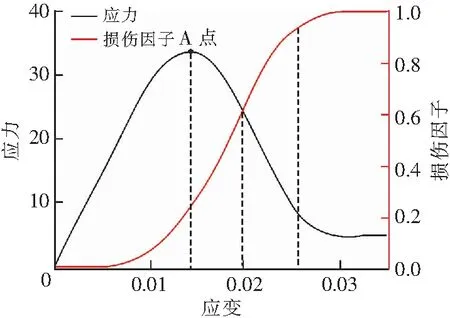
图1 应力-应变、损伤因子曲线Fig.1 Stress-strain and damage parameter curve

将εB代入损伤因子D的表达式中可得对应损伤因子为

(7)

图2 损伤速率和损伤加速度曲线Fig.2 Damage rate and acceleration curve

由式(7)可知，最大损伤速率点对应的损伤因子只由m决定，与F无关；将εB代入损伤速率表达式(3)中可得最大损伤速率为

(8)

式中e为无理数2.71.最大损伤率与F成反比例关系，损伤速率最大值由m和F共同决定与材料弹性模量无关，当损伤因子约为50%时，损伤速率的加速度为零。

通过对损伤加速度公式(7)求导后令其等于零，可得到损伤加速度最值点C、D对应的应变值，如图2所示。其中损伤加速度最大值C点应变为

(9)

将图2中C点应变值与图1中A点应变值对比后发现，损伤加速度最大值C点横坐标与峰值强度点A的应变值相同，即εc=εA.因此，当试样处于峰值强度点时，其损伤加速度达到最大值，从图1可知，此时损伤速率并不为零，对应的损伤因子为

(10)

此时对应的损伤因子仅由m决定，与F无关。

损伤加速度最小值D点代表损伤加速度达到最小值，可将此应变值作为材料残余强度点对应的应变，即

(11)

式中εe为残余强度，可见残余强度由参数F，m共同决定。将D点应变代入损伤因子表达式得

(12)

将εD,DD代入本构方程，可得残余强度σD为

(13)

经分析，D点处损伤因子约为84%，间接证明了文献[11]中“以损伤因子约等于84%时对应应变值作为残余应变”推断的正确性，因此，将损伤速率加速度最小值D点作为残余强度点，即εD=εe，具有明确的力学意义。通常认为煤岩达到残余强度时的损伤因子为1，即所有微元单元破坏，这与实际情况不符合。因为既然煤岩仍存在残余强度，就代表煤岩仍未完全破坏，这与所有微元单元破坏这描述相矛盾。

(14)

此式表明损伤加速度最大值点C和损伤加速度最小值点D处的应变值关于损伤速率最大值点B处的应变值对称。

由于传统评价指标测定实验需要采用按位移和按应力2种加载方式，增加了实验工作量。文中将峰值强度点(损伤加速度最大值点C点)作为动态损伤应变起始点，将残余强度初始应变点(损伤速率加速度最小值点)作为动态损伤破坏的结束点，即动态损伤应变为

εDT=εe-εmax

(15)

根据上述对动态损伤应变的修正，可用式(15)得到按位移加载实验中动态损伤应变与动态破坏时间的关系。从而利用动态损伤应变间接反映动态破坏时间，只需在试样达到峰值强度以后，增大数据采集频率即可提高数据精确度。

(16)

式中H为试样高度，m；V下为压头下压速度,mm/s.根据式(16)即可由动态破坏损伤应变求得动态破坏时间。

2 模型参数物理意义

2.1 损伤比例系数对应力应变曲线的影响

m反映煤岩材料内部微元强度的分布集中程度；参数F反映煤岩宏观统计平均强度的大小。保持参数E，F，m不变，研究损伤比例系数cn对应力-应变曲线的影响，如图3所示。

因为在峰值强度前煤岩损伤因子处于较低水平(一般小于0.3)，所以cn对峰值强度前的应力—应变曲线走势影响有限，可以忽略。损伤比例系数的作用主要体现在对峰值强度点及峰后破坏阶段的影响，如图3所示。峰值点后曲线最终趋于平缓的这种趋势即是煤岩材料存在残余强度的体现。损伤比例系数的取值范围是(0，1)，随着cn的减小，峰值强度略微增强，但增幅有限；同时残余强度增大、延性明显增加、残余应变降低。

图3 损伤比例系数cn对全程应力-应变曲线的影响Fig.3 Influence of variance of parameter cnon complete stress-strain curve

2.2 参数m，F对损伤因子的影响

如图4(a)所示，保持参数m不变，随着参数F增大，损伤参量曲线变得平缓，损伤持续过程增大，材料延性增大，残余应变增大；如图4(b)所示，保持参数F不变，随着参数m越大，损伤参量曲线越陡峭，损伤持续过程减短，材料脆性增强，残余应变越小，且所有损伤因子曲线过定点

(17)

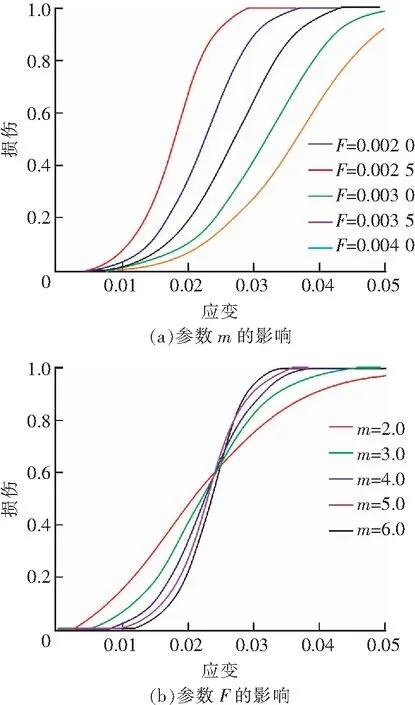
图4 参数m，F对损伤因子的影响Fig.4 Effect of m and F parameters on the damage factor

2.3 参数m，F对损伤速率的影响

如图5(a)所示，参数F不变，随着m逐渐增大，损伤速率曲线偏态减小，最大损伤速率显著增大，对应的应变值逐渐增大，最后趋于稳定；随着m逐渐增大，损伤速率越来越陡峭；如图5(b)所示，参数m不变，随着F逐渐增大，损伤速率曲线偏态增大，最大损伤速率显著减小，对应应变逐渐增大；随着F增大，曲线趋于平缓，有效应变增大，煤样脆性逐渐减弱。

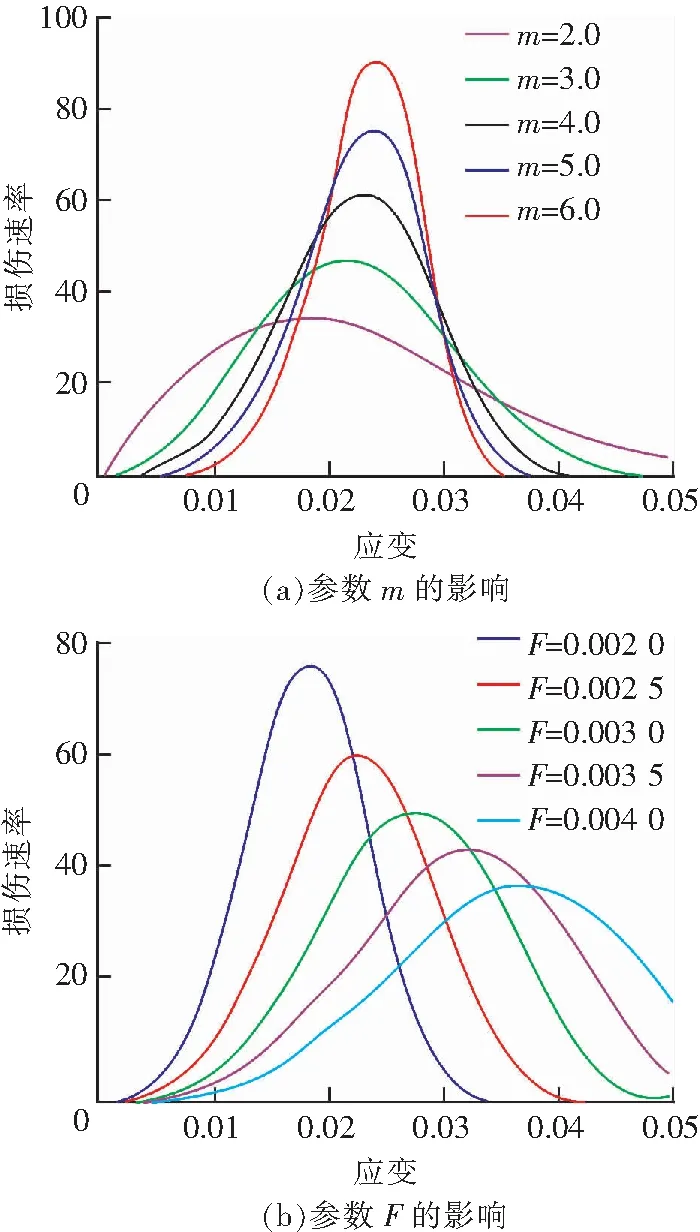
图5 参数m,F对损伤速率的影响Fig.5 Effect of m and F parameters on the damage rate

3 能量角度分析冲击倾向性指标

3.1 传统冲击倾向性指标

冲击地压是聚集在煤岩内的弹性应变能忽然释放的一种动力现象，其发生在受载煤岩残余变形阶段。通常以动态破坏时间(DT)、单轴抗压强度(Rc)、冲击能指数(KE)及弹性能指数(WET)4个指标值等作为冲击倾向性的评价指标，而将煤层冲击倾向性划分为强、弱、无3类。

冲击能指数(KE)指煤样在单轴压缩条件下的全应力-应变曲线峰值前所积蓄的变形能(AS)与峰值后损耗变形能(AX)的比值

(18)

弹性能指数(WET)指煤样在单轴压缩条件下，破坏前所积蓄的弹性变形能(Ue)与产生塑性变形所消耗的能量(Us)的比值。

在煤岩单轴压缩实验过程中，根据热力学第一定律，峰值强度前外力做功所产生的能量被煤岩弹性变形和塑性变形所消耗，则有

(19)

(20)

式中Ue为弹性应变能，J；Us为塑性应变能，J，则弹性能指数计算公式为

(21)

3.2 盈余能指数变化率指标

盈余能(剩余能)：是指峰值强度之前存储的弹性应变能与峰值后破坏过程中消耗的能量的差值，它是冲击地压的能量来源，可描述峰值前弹性能积累与峰值后破坏过程耗散能的关系。

盈余能释放速度：是指盈余能除以动态破坏时间，其物理意义是煤岩在破坏过程中单位时间内释放的剩余能量数。它将盈余能与时间结合起来，体现了冲击倾向性是关于能量和时间函数的特性。

盈余能指数：煤样盈余能与峰后破坏耗散能的比值，其物理意义是在峰后破坏过程中，煤体每耗散单位数量的变形能，伴随着释放的盈余能的数值。它将盈余能和峰后耗散能结合起来，描述了峰值强度后煤岩破坏过程中能量的变化关系。

基于以上指标，提出一种可将盈余能、峰后破坏耗散能、动态破坏时间三者相结合的新的综合性冲击倾向性评价指标-盈余能指数变化率K。其盈余能指数变化率K是盈余能除以弹性应变能和动态破坏时间所得的比值，如式(22)所示

(22)

式中WS为盈余能，J；DT为动态破坏时间，ms；Uh为峰后破坏过程消耗的变形能,J.

盈余能指数变化率既能表征煤体的剩余能量与破坏耗散能之间的相对大小，又能表征动态破坏时间。将盈余能、破坏过程损耗变形能和动态破坏时间综合起来以衡量煤层冲击性。

综上所述，以可描述残余强度特征的损伤统计本构模型为基础，利用修正后的动态损伤应变(εD)来表征动态破坏时间(DT)，确定出损伤速率最大值表达式，提出更具综合性的盈余能指数变化率指标，从而形成了新的冲击倾向性评价体系。

4 实验验证

4.1 冲击倾向性指标测定实验

主要采用DNS200电子万能实验系统，参照《煤层冲击倾向性分类及指数的测定方法》，选取3组煤样，每组3～4个，将其制成φ50×100 mm的圆柱形标准试样。

应变能测定实验的采用按位移控制的加载方式，加载速率为0.002 mm/s，采样间隔为200 ms；测定动态破坏时间实验采用按应力控制的加载方式，加载速率为0.1 kN/s，采样间隔为5 ms.

4.2 实验结果

各组实验数据利用最小二乘法反演得到模型参数F,m,cn，从而得到能反映实验曲线的本构方程。进而分别利用公式(18)、(19)、(20)、(21)、(22)求解冲击能、弹性能、峰值损伤速率、盈余能指数变化率。根据第1组、第2组实验数据直接获取动态破坏应变，进而利用公式(16)来求解动态破坏应变；根据第三组实验数据直接获取动态破坏时间，也由公式(16)求解动态损伤应变。各组煤样的模型拟合参数、传统评价指标、新增指标体系见表1.

1)利用Matlab软件提供的最小二乘法函数Lsqcurvefit反演出各组煤样的模型参数，反演结果表明，理论分析与实验曲线吻合度较好(图6)，从而验证了理论模型的合理性。在实验加载初期，煤样要经过原生裂隙闭合的过程(即实验曲线在线弹性阶段前会有明显的上凹阶段)，但文中所述的本构模型对此并不涉及，从而导致理论和实验结果存在一定的误差，如图6(a)所示；当煤体原生裂隙越少、脆性越强，则误差越小，如图6(b)所示。

图6 实验曲线与损伤本构模型理论曲线对比Fig.6 Comparison between experimental curve and theoretical curve for damage constitutive model

显然，理论分析偏向于将冲击倾向性判定为危险程度更高的方面，只要将上述误差控制在一定范围之内，则该模型仍是可接受的。

2)修正后的动态损伤应变和动态破坏时间具有明显的相关性。因此，利用动态损伤应变表征动态破坏时间是切实可行的。直接根据实验曲线来求解冲击倾向性指标值的传统方法误差较大，而文中所述根据实验数据反演损伤统计本构模型的参数，再据此求解冲击倾向性指标的思路是可取且准确的。根据动态损伤应变与动态破坏时间的关系式(16)，二者即可相互转化，从而避免了传统冲击倾向性实验受加载方式限制的问题，减少实验工作量。

3)煤体脆性越强，在峰值强度前积累的弹性应变能越多，则峰值强度后盈余能释放形式越猛烈，动态损伤应变和动态破坏时间数值越小，盈余能指数变化率指标越大，煤体在破坏过程中伴随的碎块弹射现象越明显，最终煤体冲击倾向性越强，这与之前研究结果相吻合。

4)各煤样的冲击倾向性危险等级是根据传统评价指标来确定的，结果显示：第1组和第3组冲击倾向性危险等级为“弱”，第2组冲击倾向性为“无”。新提出的冲击倾向性指标体系可由模型参数直接求解，其灵敏度较高，与传统指标体系吻合度较好，作为新的冲击倾向性指标是切实可行的。

表1 冲击倾向性实验测定结果及模型计算结果

5 结 论

1)考虑残余强度的损伤统计本构模型能较好的反映煤岩材料峰值强度后的应力-应变曲线的变化趋势及残余强度特点，为评价煤层冲击倾向性奠定了理论基础。

2)基于损伤速率提出损伤加速度概念，并得到峰值强度点、损伤速率最值点、损伤加速度最值点处的应力、应变及损伤因子的表达式，进而获得可间接表征动态破坏时间的修正动态损伤应变，使冲击倾向性实验不再受加载方式的限制。

3)提出一种评价煤岩冲击倾向性的新指标-盈余能指数变化率指标，且将盈余能指数变化率、损伤速率最大值和修正后动态损伤应变构成冲击倾向性评价新的指标体系。利用冲击倾向性实验表明，新提出的冲击倾向性指标评价结果稳定可靠，能有效减小评价误差和降低实验工作量。