基于模糊Petri网的城市突发性燃气短缺应急能力评估*

陆秋琴，王 勃，黄光球

(西安建筑科技大学 管理学院，陕西 西安 710055)

0 引言

燃气已经处于城市能源组成部分的核心地位，在IEA成员国中，有16个国家的城市燃气(即天然气、液化气)消耗量超过一次能源消耗总量的20%，其中7个国家超过30%[1]。我国现在正处于城市化、工业化的高速发展阶段，城市的燃气普及率已经高达98.42%，每年的燃气供应总量约2 803亿m3。随着近年来城市燃气供需缺口日益扩大、极端气候、突发事故等方面的影响，导致城市的“气荒”情况越来越严重，可能造成工业生产和电力供应停滞，社会经济活动和日常生活难以正常运行；同时也可能引起社会的恐慌，短时间内激发消费需求，引起消费剧增、价格暴涨，对社会稳定造成严重的影响[2]。因此，针对城市愈演愈烈的“气荒”状况，通过对城市燃气短缺应急体系的评估，找出影响城市燃气短缺应急能力的主要因素，提出科学、有效的应对策略，对提高城市突发性燃气短缺的应急能力具有一定的现实意义，同时也有助于减少由城市突发性燃气短缺事故引起的各类经济损失。

针对以上不足，本文提出一种基于模糊Petri网的城市突发性燃气短缺应急能力评估模型，该模型基于应急能力影响因素间的关联过程，评价城市突发性燃气短缺应急能力。该评估模型具有以下特点：

1)该模型能够结合评估体系中一些模糊或不确定的影响因素，根据层次化的模拟仿真对影响因素众多且因素间信息反馈不明确的复杂城市突发性燃气短缺应急能力进行评估。

2)该评估模型系统全面地从应急的多个方面来构建应急能力影响因素体系，同时可以从不同层次间动态的应急反馈过程，形象、直观地显示城市突发性应急过程中的逻辑因果关系与机理，图形化、科学化地对应急过程进行仿真分析。

3)该模型的仿真过程通过采用极大代数运算来提高整体模型运算效率，同时采用AHP来减少应急影响因素的评估主观性，可以更加合理、有效地对城市突发性燃气短缺应急能力进行评估。

1 应急能力评估指标体系

1.1 指标体系构建准则及步骤

城市突发性燃气短缺应急能力是指从城市整体应急系统的角度出发，通过政府部门的指挥决策、法规制度、应急预案以及企业、人员、设备积极响应等各方面因素参与下，对城市突发性燃气短缺应急全过程的紧急应对与事后恢复能力。在城市突发性燃气短缺应急能力评估过程中，评估指标体系的构建是最关键的一个环节，它将直接影响应急能力评估结果的科学性、全面性、可比性及有效性，但是影响城市突发性燃气短缺应急能力的各类因素中存在大量的主观性与不确定性、耦合性的问题，因此必须用合适的评估准则进行深入地剖析来确定应急能力评估体系。本文从应急能力评估的目标出发，综合考虑了法律制度、人员、设备、管理、指挥决策等因素，在筛选具体指标时以系统性、科学性、可行性为指导原则，遵循了(P)计划-(D)实施-(C)检验-(A)改进的构建程序[14]，建立能够综合反映城市突发性燃气短缺应急能力状况的应急指标体系。构建步骤如图1所示。

图1 城市突发性燃气短缺应急评估指标体系构建步骤Fig.1 Construction steps of index system for emergency assessment of urban sudden gas shortage

1.2 评估指标体系的构建

城市突发性燃气短缺应急是一个多阶段且复杂的反馈综合应急网络体系，由监测预警体系、资源保障体系、应急响应体系、应急组织体系、后期恢复评估体系5个子体系共同构成，各个子体系在城市突发性燃气短缺事件发生过程中，共同对城市突发性燃气短缺应急能力发挥着至关重要的作用。通过对应急系统影响因素内容以及文献[12]分析，建立包括5个二级指标和26个三级指标的城市突发性燃气短缺应急能力评估体系，如表1所示。

表1 城市突发性燃气短缺应急能力评估指标体系Table 1 Index system for emergency capability assessment of urban sudden gas shortage

1.3 应急能力等级评判标准

表2 应急能力等级评价标准Table 2 Assessment criteria of emergency capability grade

2 FPN评估模型及推理算法

2.1 模糊Petri网模型的定义

模糊Petri网是根据传统Petri网不能处理评价指标的不确定性和模糊性的特征扩展而来，通过模糊集理论形成模糊Petri网评价体系来描述具有模糊行为的并发系统，因此被广泛应用于各个复杂系统的模拟仿真等实际问题。城市突发性燃气短缺应急是一个复杂动态过程，模糊Petri网可以很好地展现出应急行为变迁与反馈过程，还可以通过推理分析出影响因素之间的因果关系。

为了更明确地表达城市突发性燃气短缺应急能力评价的模糊Petri网(USGSFPN)，将其定义为1个8元组，如式(1)所示。

USGSFPN=(P,T,D,IN,OUT,V,λ,M)

(1)

2.2 产生式规则的模糊FPN表示

根据USGSFPN的定义，每1个变迁都可以被看成是1个运行规则，那么变迁的输入库所(d1,d2,d3,,dn)和输出库所(dg)分别表示运行规则的前提条件和结论命题，可以通过逻辑联接符号“and”或“or”进行因果表示。通过对城市突发性燃气短缺应急能力评估体系分析，认为应急系统中的某1个影响因素可能就会导致整体应急能力下降。即IFd1(w1) ord2(w2)or,,ordn(wn)，THENdg(wg1)，变迁发生规则以及触发规则如图2所示。变迁的可信度数学表达式如式(2)所示[14]：

wg1=max(w1μ1，w2μ2,,wnμn)

(2)

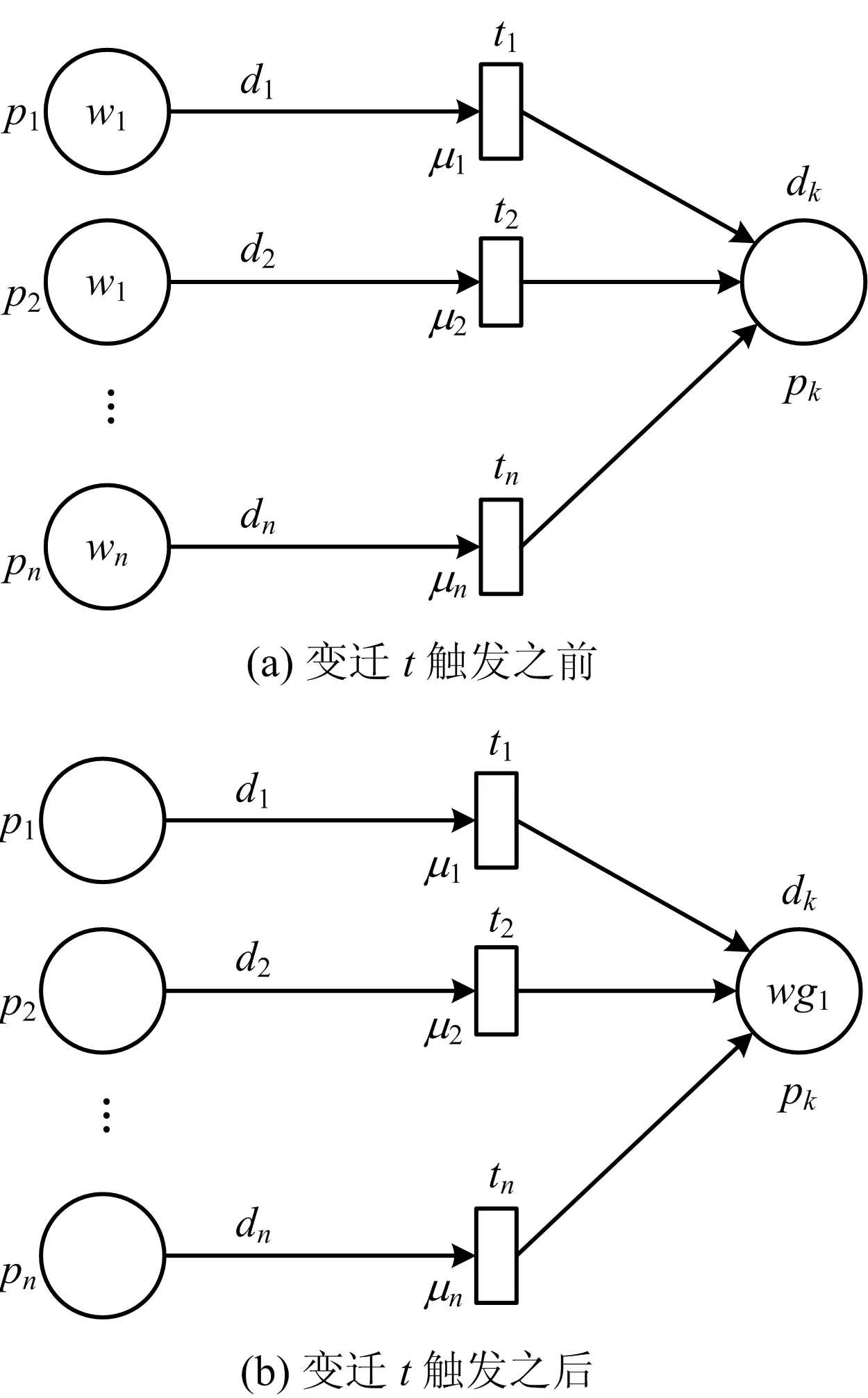
图2 USGSPFN模型推理规则Fig.2 Inference rules of USGSPFN model

2.3 模糊矩阵推理算法及步骤

1)模糊推理算法

在USGSFPN模糊推理之前，为了清晰、准确、简洁地表达推理矩阵运算，推理过程中引入以下算子：设A,B,C均为n×m维矩阵，D为n维向量[16]，则有：

①加法算子⊕:A⊕B=C,则有cij=max(aij,bij),(i=1,2,,n;j=1,2,,m)

②乘法算子⊗:D⊗B=C,则有cij=di×bij,(i=1,2，,n;j=1,2,,m)

2)USGSFPN模糊推理步骤

根据相关算子规则进行模糊推理运算。首先将城市突发性燃气短缺应急能力评估体系转化为USGSFPN网模型，根据模糊Petri网的USGSFPN定义分别确定应急能力影响因素集IN与应急行为集OUT，其中|P|=n，|T|=m，相应矩阵形式分别为IN={αij}，OUT={γji}；然后根据历史数据与应急专家知识库数据评估标准得到初状态M(0)；根据层次分析法可得到应急系统中各个应急影响因素的权重值ωi，同时得到模糊变迁的置信度向量U={Ui}={ωi}。具体模糊推理计算步骤如下所示，其中，输入包括：初始化输入矩阵IN；输出矩阵OUT；置信度向量U；应急能力评判矩阵Q和初始状态矩阵M(0)。输出包括：各个库所应急能力评估值。

①步骤一：令初始状态k=0，变迁发生时，初始应急能力影响因素输入库所的可信度INTM(K)；变迁触发后，应急行为输出库所的可信度U⊗OUT。

②步骤二：计算变迁触发生后的下一个状态，应急能力影响因素行为变更的可信度为M(k+1)=M(k)⊕(U⊗OUT)[INTM(k)]。

③步骤三：若M(k+1)≠M(k)，则令k=k+1，转到步骤二；若M(k+1)=M(k)，则模糊推理结束。

④步骤四：计算各个库所应急能力等级F=M(k)QT，F为n×1阶矩阵，表示n个库所的应急能力评估等级值,该矩阵的最后1个元素对应的等级标准即为城市突发性燃气短缺应急能力指标综合等级。

3 实例仿真

3.1 构建FPN模型

为了验证上述应急能力模型和模糊推理算法的可行性和科学性，本文以西安市突发性燃气短缺应急为例进行模拟仿真分析。通过基本的模糊规则逻辑关系将城市突发性燃气短缺应急能力评估指标体系(表1)转化为FPN模型，如图3所示。

图3 城市突发性燃气短缺应急能力评估体系FPN模型Fig.3 FPN model of emergency capability assessment system for urban sudden gas shortage

3.2 FPN应急能力评估参数求解

根据USGSFPN的定义，可得到城市突发性燃气短缺应急FPN模型的输入矩阵IN和输出矩阵OUT，通过查阅《西安市统计年鉴2018》、相关历史数据以及城市应急专家知识库等,以及分析历史数据和专家评判法给出的库所评估向量取值量化规则可得到初始评估向量矩阵M(0)，如式(3)所示。

(3)

IN={αij},α1,1=1,α2,2=1,α3,3=1,α4,4=1,α5,5=1,α6,6=1,α7,7=1,α8,8=1,α9,9=1,α10,10=1,α11,11=1,α12,12=1,α13,13=1,α14,14=1,α15,15=1,α16,16=1,α17,17=1,α18,18=1,α19,19=1,α20,20=1,α21,21=1,α22,22=1,α23,23=1,α24,24=1,α25,25=1,α26,26=1,α27,27=1,α28,28=1,α29,29=1,α30,30=1,α31,31=1,其余的输入值αij=0,(i=1,2,,n;j=1,2,,m)。

OUT={γij},γ1,27=1,γ2,27=1,γ3,27=1,γ4,27=1,γ5,27=1,γ6,28=1,γ7,28=1,γ8,28=1,γ9,28=1,γ10,28=1,γ11,29=1,γ12,29=1,γ13,29=1,γ14,29=1,γ15,29=1,γ16,29=1,γ17,29=1,γ18,30=1,γ19,30=1,γ20,30=1,γ21,30=1,γ22,30=1,γ23,31=1,γ24,31=1,γ25,31=1,γ26,31=1,γ27,32=1,γ28,32=1,γ29,32=1,γ30,32=1,γ31,32=1,其余的输出值γij=0,(i=1,2,,n;j=1,2,,m)。

3.3 影响因素的权重值计算

计算各影响因素的权重值(即变迁的置信度向量U)，根据城市突发性燃气短缺应急评估体系，以二级指标为例，通过层次分析法从应急预警(B1)、资源保障(B2)、应急响应(B3)、应急组织(B4)、后期恢复评估(B5)等5个方面确定指标权重，根据指标重要程度采用1～9标度法得到判断矩阵A-Bi。经归一化处理后的权重值如表3所示。判断矩阵A-Bi的λmax=5.353 239，CI=0.088 31,RI=1.12，进而求得CR=0.078 8<0.1,满足一致性检验。

表3 A-Bi层判断矩阵及指标权重Table 3 A-Bi layer judgment matrix and index weights

同理可得其他各变迁的置信度向量为：U={0.30,0.43,0.14,0.08,0.05,0.46,0.18,0.23,0.09,0.04,0.49,0.14,0.05,0.16,0.16,0.28,0.36,0.05,0.10,0.11,0.07,0.03,0.08,0.48,0.20,0.19,0.04,0.53,0.27,0.15,0.05}。

3.4 模糊推理运算

根据USGSFPN模糊推理步骤，利用MATLAB软件进行模糊运算，由推理算法程序进行迭代得到最终的M(k)为：

M(2)=M(3)=[

根据最后一个元素为5.424,表明了西安市突发性燃气短缺应急能力等级为中等；二级指标中，监测预警能力为6.078，表明监测预警方面能力等级较高;资源保障能力为6.204，表明资源保障方面应急能力等级较高;应急响应能力为4.974，表明应急响应能力等级中等;应急组织能力为5.464，表明应急组织能力等级中等;后期处理能力5.572，表明后期恢复评估能力等级中等。三级指标应急能力等级限于篇幅不详细列出。

3.5 分析及建议

在USGSFPN评估模型中，由于上层指标支配着下层指标，同时下层指标共同制约着上层指标，因此使用下层指标评估等级均值来作为下层指标对上层指标的制约相关性阀值，若下层指标评估等级值低于阀值，则对上层指标的制约相关性越强。根据上述方法和仿真计算结果显示，西安市突发性燃气短缺应急能力水平为中等，制约综合应急能力的二级指标主要有应急响应能力、应急组织能力、后期恢复评估能力(阀值=5.658 4)。同理，通过数值分析可得对上述3个二级指标制约相关性较强的三级指标，并根据其相应的不足对提升西安市突发性燃气短缺应急能力提出建议。

1)在应急响应能力方面，应建立应急专项领导小组加强城市突发性事件应急指挥决策反应能力，总结、积累应急事件经验，不断完善突发性事件应急预案的完整性，建立应急响应的预演机制、加强宣传力度，使得政府和民众应急响应能力进一步提升。

2)在应急组织能力方面，精简应急单位、部门的数量并且做到明确应急组织的责任划分，建立城市区域间的联动协调机制，不断提升应急组织效率的同时，也提高应急组织能力的快速化和实效性。

3)在后期恢复评估能力方面，需要加强对应急专业队伍的建设和后期恢复资金的投入，来提高事后评估的准确性、减少恢复的时间，加强突发性事件后期恢复评估能力的建设也是为应急能力的不断提升打下坚实的基础。

4 结论

1)本文提出的模糊Petri网方法综合考虑了系统中的各种影响因素，通过模糊推理和算法得到应急能力等级评价指标，在某种程度上避免了影响因素分析的不确定性和主观性问题，使应急能力评估结果更加准确、有效。

2)通过对模糊Petri网模型及其推理算法在城市突发性燃气短缺应急能力评价中的应用，表明该方法不仅能够评估城市应急系统综合的应急能力等级，而且还能评估各个子系统的影响因素以及中间层的应急能力等级，具有可行性、科学性和准确性的特点。

3)以西安市突发性燃气短缺应急为例进行模拟仿真分析，最终根据模拟仿真结果，在应急响应能力、应急组织能力、后期恢复评估能力等3个方面提出措施建议。