常用经验模型预测煤屑瓦斯解吸量对比分析*

2019-10-16张宪尚

中国安全生产科学技术 2019年9期

张宪尚

(1.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037；2.中煤科工集团重庆研究院有限公司，重庆 400037；3.四川大学，四川成都 610065)

0 引言

研究煤屑瓦斯解吸扩散特征，对于探索煤矿井下瓦斯涌出、预测煤与瓦斯突出、煤层瓦斯赋存参数测定及煤层气产能预测等方面具有重要实际意义[1-4]。国内外学者针对不同条件煤屑瓦斯解吸特征进行大量试验研究并总结得到不同的经验模型，如Barrer[5]依据甲烷气体分子在天然沸石中解吸规律试验研究，提出表达气体累计解吸量和时间关系的巴雷尔式；Airey[6]研究碎煤瓦斯解吸扩散规律，得到艾黎经验公式；Bolt等[7]对试验研究不同变质程度煤的瓦斯放散过程并总结出博特式；孙重旭等[8]认为累计瓦斯解吸量与时间成幂函数关系;王佑安等[9]将煤样解吸环境快速降至真空，总结得到出王佑安经验表达公式;宋世钊[10]在译著中介绍了前苏联的研究煤中瓦斯解吸量与时间关系的乌斯基诺夫式。

以上经验模型是根据不同试验条件和分析角度得到的，存在一定适用范围并可以在一些特定环境下相互转化[11-12]。如巴雷尔公式在地勘期间硬煤取芯推算瓦斯损失量方面得到广泛应用，但却不适于构造煤的瓦斯损失量的推算[13]；艾黎式明显低估了瓦斯解吸开始阶段的放散量[11]。根据瓦斯放散量与时间关系及公式特点，这些经验模型大致可分为幂函数式和指数式2大类，幂函数则被认为煤样暴露后60 s内的瓦斯放散速度理想的公式[14]。在实际应用过程中，多利用这些经验模型拟合瓦斯累计解吸量随时间的变化数据并都表现出较高的拟合度，但对各个经验模型拟合后瓦斯累计解吸量的预测方面关注较少。

本文在试验测定煤屑瓦斯累计解吸量的基础上，取初期不同时间段瓦斯累计放散量数据拟合得到经验模型参数，将模型参数代入到经验模型中计算出不同时间的瓦斯解吸量，并将其结果与试验测定值进行对比。该研究对经验模型在煤的瓦斯涌出及煤层气产能预测方面有着重要实际意义。

1 煤屑瓦斯累计解吸量的试验测定

1.1 试验样品

试验样品采取宁夏汝箕沟矿3号煤层335工作面煤样，按标准破碎、筛分成粒度1～3 mm的质量100 g样品备用。样品的密度、工业分析及瓦斯等温吸附参数见表1。

表1 试验样品的工业分析及等温吸附参数

1.2 试验设备

煤屑瓦斯的解吸扩散属于一种传质过程，该过程受煤屑周围气体压力、环境温度及煤屑内部孔裂结构特征等因素影响，其测定方法一般主要分为重量法和容量法2种，重量法是根据吸附剂(煤屑)解吸前后质量变化测定得到解吸量，而容量法则根据解吸前后固定体积气体压力的变化测定解吸的大小[15]。试验系统主要是由法国Setaram公司研制的全自动siverts型高压气体吸、解吸分析仪PCTPro-evo组成，试验系统实物如图1所示。

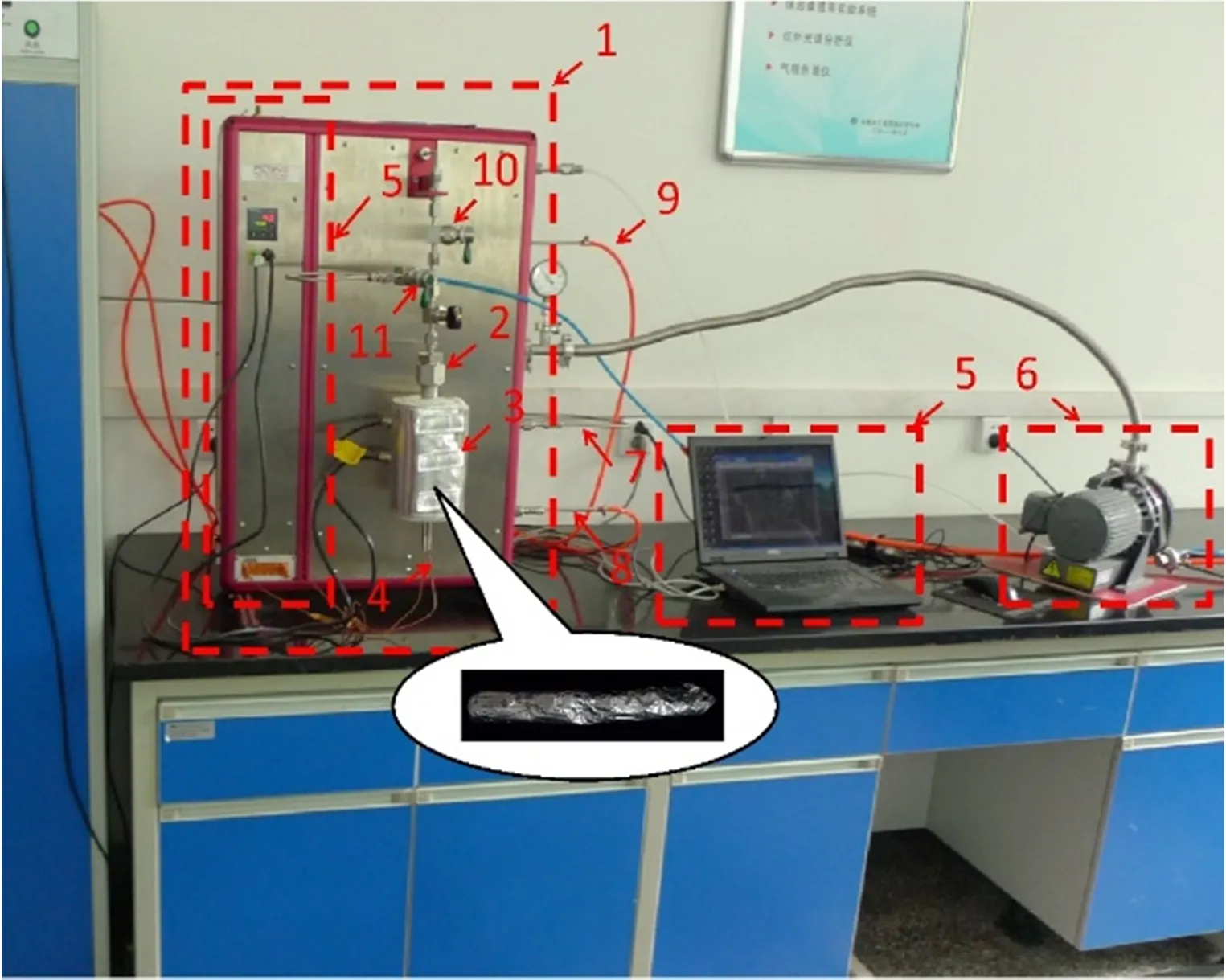
1-PCTPro-evo仪器；2-试验样品池;3-加热套;4-热电偶;5-数据采集及控制系统;6-干式真空泵;7-甲烷气体气路;8-氮气气体气路;9-氦气气体气路；10-阀门；11-阀门。图1 PCTPro-evo吸附解吸试验系统Fig.1 PCTPro-evo adsorption and desorption test system

1.3 试验步骤及结果

1)将待测煤样取30 g左右，用高精度电子称详细称取煤样质量并记录，利用锡纸包裹装入样品池中并连接仪器，装好加热套等。

2)开启真空泵，开启吸附解吸测定仪，对仪器进行自检及气密性检测。

3)气密性检测合格后，设定温度达到60 ℃进行抽真空6 h以上。

4)设定吸附温度为30 ℃，待仪器温度稳定后，进行自由空间校准。

5)设置吸附压力，并设置吸附平衡判别标准。

6)样品吸附平衡后，关闭阀门10，对仪器进行解吸测定设置，将参考罐中气体压力设定为大气压压力。

7)开启阀门11，放空2 min模拟钻取煤样的暴露过程，关闭阀门11，开启阀门10，进行瓦斯解吸累计量测定，如图2所示。

图2 累计瓦斯解吸量Fig.2 Cumulative amount of gas desorption

8)瓦斯解吸测定完成后，关闭测试软件及仪器设备。

2 经验模型拟合

2.1 经验模型回归拟合分析

对于含有瓦斯的煤屑解吸放散过程，在煤屑暴露瞬间，只是煤屑外面附近的瓦斯开始涌出。随着时间的增长，煤屑深部的瓦斯也开始运移，瓦斯运移界面逐渐缩小，瓦斯流动通道长度增加，运动阻力增大，当瓦斯流场长度达到煤屑半径后，煤屑中心的瓦斯压力将相应地降低。因此，瓦斯煤屑中的放散速度随着时间的延长而降低，描述这一衰减过程的经验方程有[12]：巴雷尔式、抚顺式、重庆式、博特式、艾黎式、文特式、乌斯季诺夫式、指数式、模拟近似式等。对于特定煤样，在其吸附解吸环境一定的情况下，当时间趋于无穷时，其瓦斯解吸量是恒定的，因此在实际的拟合过程中，不同公式的形式可以转化成相同的拟合形式，如文特式与重庆式。由于试验测定是煤屑暴露后的瓦斯解吸量，因此需要考虑暴露期间的瓦斯损失量，故拟合公式中出现常数项，并选取暴露时间后解吸5，10，30，60 min的数据，利用origin软件对其进行拟合得到不同经验公式的参数值，详见表2。

2.2 回归拟合过程及效果分析

利用origin软件采用Levenberg Marquardt算法对瓦斯累计解吸量随时间变化的数据进行回归拟合分析，其经验公式回归分析得到的各个参数受到迭代初始值的限制，因此对同一经验模型回归分析过程中需要设置初始值时，保持初始值一致或按照参数随时间变化设置。

表2 各经验模型公式拟合参数值

表2(续)

从确定系数R-Square(详见图3)值大小可以看出[16]，不同公式拟合过程中确定系数都接近1，表明模型公式的变量对数据解释能力较强，模型对数据拟合效果也较好，其拟合效果好劣程度依次为：巴雷尔式<博特-指数式<抚顺式<模拟近似式<重庆-文特式<乌斯季诺夫式<艾黎式。随着采取数据时间段的增加，重庆-文特式、乌斯季诺夫式及艾黎式的确定系数R-Square变化平稳，拟合效果不会随着数据多少而发生变化，而其他经验模型公式随着数据的增多而减低，其中巴雷尔式降低尤为明显。

3 瓦斯解吸量预测对比

为了分析不同经验模型公式对煤屑瓦斯解吸的预测能力，分别取不同时间段模型参数值代入经验公式得到不同时间的累计瓦斯解吸量，并与试验测定值进行对比，如图4所示。

从图4中可以看出，巴雷尔式明显高估拟合时间段后的累计瓦斯解吸量，不适合对累计瓦斯解吸量进行预测，而指数型经验模型曲线在拟合时间段后很快趋于平直，而低估拟合后累计瓦斯解吸量；对采用5 min和10min时间段的数据拟合参数的各个经验模型中，乌斯季诺夫式及重庆式都表现出较高的瓦斯解吸量预测能力，这与文献[17]结论相一致，特别是5 min时间段数据拟合参数的乌斯季诺夫式，但从初期的累计瓦斯解吸量对比中可以看出乌斯季诺夫式明显高估了煤屑瓦斯解吸量，期间预测能力表现不如重庆式；对30 min和60 min时间段的数据拟合参数的各个经验模型中，重庆式及艾黎式都表现出较好的瓦斯解吸量预测能力，特别是艾黎式在长期的累计瓦斯解吸量中有较好的预测能力。

图3 不同时间段数据回归分析的确定系数Fig.3 Determination coefficients for regression analysis of data in different time periods

图4 经验模型公式瓦斯解吸量预测与对比Fig.4 Prediction and comparison of gas desorption amount based on empirical model formulas

为分析不同时间段数据量对经验模型的预测能力影响规律，特选博特-指数式、艾黎式、乌斯季诺夫式及重庆-文特式不同时间段拟合计算得到的曲线与实际试验测定曲线进行对比，如图5所示。

随着瓦斯解吸数据时间段的增长，博特-指数式、艾黎式及重庆-文特式计算得到累计瓦斯解吸量曲线越来越接近于实际测定得到瓦斯解吸量曲线，而乌斯季诺夫式随着瓦斯解吸量数据时间段增长而远离实际测定曲线，其中博特-指数式和乌斯季诺夫式会随着时间段延长呈现出规律性接近或远离。随着时间段的增长，对于各个经验模型计算得到曲线而言：博特-指数式在拟合时间段后很快趋于稳定平直，低估煤屑长期瓦斯解吸量，这与指数衰减的拟合形式有关；艾黎式接近实际测定曲线速度最快，在长时间段瓦斯解吸数据预测累计解吸量表现最好；在利用较短时间煤屑瓦斯解吸量数据预测长期瓦斯解吸时，乌斯季诺夫式表现最好。