月牙定理背后的千年传奇——从一道高考题说开去

韦 磊

在2018年高考数学全国卷中，有这么一道题，骨骼清奇：

【原题】下面是来自古希腊数学家希波克拉底的几何图形，此图由三个半圆构成.三个半圆的直径分别是直角三角形ABC的三边AB，AC，BC，三角形ABC围成的区域记为Ⅰ，斜线阴影部分的区域记为Ⅱ，白色部分记为Ⅲ，在整个图形中任取一点，此点取自各部分的概率分别为P1，P2，P3，则（ ）

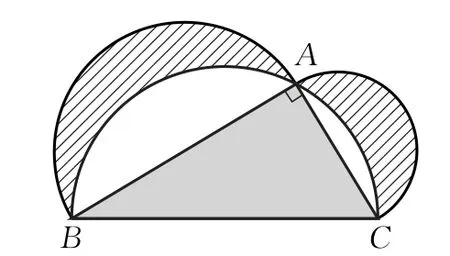
图1

A.P1＝P2B.P1＝P3

C.P2＝P3D.P1＝P2＋P3

此题难度倒是不大，通过简单的勾股定理即可得.

设白色部分面积为S1，

直角边上的两个半圆面积为：

这显然同直角三角形的面积相同.所以答案是A.

当然清奇之处倒不是此题的难度，而是它不凡的背景.

这个故事，说起来真的是荡气回肠.这个故事，就是著名的化圆为方.

注：“化圆为方”是古希腊数学尺规作图领域中的命题，它与“三等分角”“倍立方问题”并列为尺规作图三大难题.

一、数与形的竞争，形的胜出

古人从现实生活中逐渐提炼出基本的数学概念，并且这些概念结论什么的逐渐分成两大阵营——几何与算术.这两门学科不像现在那般相互促进，而是在相互竞争——谁管用就信谁.当几何中有了新的发现，几何便占据优势，算术渐被多数人忽视；而当算术有了新的发现，算术又取代几何的位置成为主流.

毕达哥拉斯学派大概是以著名的毕达哥拉斯定理（也就是勾股定理）而让我们熟知.实际上这只是毕氏学派在几何中的一大贡献而已，他们在算术中的思想往往被我们忽视——大概是这种思想被证明是一种荒谬之故——“万物皆数”.

这种思想认为，所有的数都能用两个整数的比值来表示，换成我们今天的话说，那就是所有的数都是有理数.这在我们现在看来显然是荒谬的，不过在那时，这条原则被奉为圭臬，成为毕达哥拉斯学派的核心教义.这里用教义一词，并非误用，因为从很多方面看，毕达哥拉斯学派都不像我们印象之中的学术团体，而更像一个宗教团体.

我们提起这种思想是想让大家知道，毕氏学派一开始是在几何与算术两大阵营都有建树的，并无偏颇一方之意.但“成也萧何，败也萧何”，毕氏学派因该定理流传千古，也因该定理毁了自己的思想根基——正是因为毕达哥拉斯定理导致了“无理数”的发现.因为他们发现，直角边都为1的直角三角形的斜边，没办法用两个整数的比值来表示.这对毕氏学派来说是灾难性的，对人类来说却是一大喜事.

发现这一现象的，正是毕氏学派的弟子.据说，他因此付出了生命的代价，怒不可遏的其他弟子将其沉入海中.虽然这一点没有得到证实，但这反映出了毕氏学派的宗教性质——不愿意接受异见.

然而不可公度数的发现，并没有引导人们去进一步研究数的性质，反倒让人们对算术失去了信心，就从这个节骨眼开始，几何对算术的优势一直支配着希腊，足有一千多年.

二、对面积的痴迷，对美和秩序的追求

古希腊人被几何的对称性、视觉美和微妙的逻辑结构吸引住了，尤其是化繁为简的处理方式，即以简单和基本的东西作为复杂和纷繁问题的处理基础.

如果要从大自然中直观体验到一两种几何体，那么最常见的莫过于直线和圆了.对直线和圆的痴迷，使得直尺和圆规成为了几何作图的核心工具（至少在古希腊是如此），而直尺和圆规的实用性反过来增进了直线和圆在古希腊几何学中的地位.

出于对几何中美和对称性的追求，古希腊人开始研究起面积，其本意我猜测是想把描述平面图大小的量转化成简单的正方形.面对着一般图形求面积的困难，古希腊人心中就萌发“用一个正方形面积取代一个平面图形的面积”的想法.因为如果能实现，那么规则对称的正方形替换了不规则不对称的平面图形，这是一种以对称取代不对称，以完美取代不完美，以有理性取代无理性的过程，也是宇宙所固有的简约和美的象征.

为了更彻底地反映这种科学精神，古希腊数学家们还对圆规和直尺的用途加以限制：圆规只能画圆，而直尺，是没有刻度的直尺，只能画直线.

三、直边图形的遗憾，月牙定理的“曙光”

凭着古希腊人的才华，人们已经能仅凭“尺规作图”，用正方形的面积表示任何“直边图形”的面积，但曲边图形却遇到了困难.人们起初怀疑这种方案的可行性，因为直觉认为尺规不能将曲边拉直.然而希波克拉底带着他的月牙定理，让众人看到了“化曲为直”的希望.如下图所示：

以直角三角形三边为直径作半圆，两两相交成图中所示两个阴影月牙形，则两个阴影月牙形面积之和等于直角三角形面积.

如图2，S1＋S2＝S△ABC.

图2

该定理一面世便引起轩然大波，太提神了！一个曲边图形的面积就这样等于了一个直边图形的面积，这对于那些一心想寻找化曲为直的数学家来说实在是太振奋人心了.有传言称希波克拉底个人都据此宣称他已经解决化圆为方问题，在后来的辛普利西乌斯的转述中提到所谓的“化圆为方”问题解决办法.后来证实这是错误的——作者错误地将此月牙推广到任意月牙：

图3

如图3所示，作者认为黑色部分和灰色部分面积相同.这显然只是很不负责任的推广，稍加计算便可得知其错误.实际上直到20世纪，数学家们才证明仅存在五种月牙形能用正方形来表示面积.当然这是后话，不管是非如何，月牙定理确实激起了大家对“化圆为方”问题的兴趣，而且他们如此着迷，一做就是两千多年……

四、千年后的终结

两千多年来，尽管无数的数学家为几大几何作图问题费尽心思却仍未有任何突破，但人们始终相信，这些都只是数学家们的能力不够而已.直到1882年，德国的费迪南德·林德曼证明了该问题的不可能性——根本原因就在于圆周率π的超越性，这个问题才算得到了圆满的解决.

所谓超越数，这是一个比较复杂的概念，你可以理解成比一般的无理数更为“无理”的无理数.

数学家证明，只要是超越数，仅仅使用我们的尺规，是没办法做出来的.而我们的“化圆为方”，实际上就是做出长为的线段，由于π的超越性，这是没办法做出来的，也就证明了“化圆为方”是不可能的.

但若是没有尺规的这个限制，“化圆为方”之类的问题还是很容易解决的.比如说：将圆滚一圈就滚成直线，然后再对直线四等分就行了.

回顾整个历史的发展过程，当人们最初提到用尺规化圆为方时，人们直觉认为这是不可能的，但是月牙定理颠覆了直觉；而后，林德曼等人的否定结论表示，直觉并非都错——对于“化圆为方”问题来说，直觉永远都是对的.

更有戏剧性的是，当初是因为不可公度数的出现，使得人们认为代数不可靠，转而去研究几何；而几何上的问题最终却成为了代数问题.什么叫数形结合？这就是.

顺便提一句，关于无理数的困扰之类，在我们中国人这里从来都不是问题，虽然我们早已发现勾股定理.倒不是我们比别人领先，而是我们压根就没有意识到这是一个问题.我们的数学大多是作为算术之用，我们可以取到根号2的任意精确的值，至于他最终是什么，我们没有关心过.

历经千年，只为证明人们的直觉.当然，历经千年的洗礼，虽然最终回归到了直觉，但我们的思维，早已超越.