基坑开挖引起下卧盾构隧道转动与错台变形计算

2019-10-16

中南大学学报（自然科学版） 2019年9期

(1.浙江大学建筑工程学院，浙江杭州，310058；2.浙江大学城市学院土木工程系，浙江杭州，310015)

随着城市轨道交通发展和地下空间的开发利用，在运营地铁隧道附近进行基坑开挖的工程越来越多[1]，包括一些在已有盾构隧道上方进行基坑开挖的工程，如杭州延安路地下通道基坑跨越地铁1号线[2]、上海广场基坑跨越地铁1号线区间隧道[3]以及上海浦东新区东方路下立交工程基坑跨越地铁2号线[4]。当此类工程的基坑开挖时，开挖面卸荷作用会通过土体传递给下方盾构隧道，在隧道结构上引起附加荷载，破坏管片结构的受力平衡，从而产生变形，甚至损伤。为保证轨道线路安全运营，地铁隧道对变形控制要求较高[5]。因此，研究基坑开挖对下卧盾构隧道的影响具有重要的应用价值。针对此类工程问题，国内外已展开了一些研究。研究方法主要可归纳为：实测数据统计分析[6-7]、数值模拟[8-9]、理论计算[10-12]和离心模型试验[13]。在理论分析法方面，王涛等[14]用Boussinesq解计算开挖卸载产生的附加应力，将下卧隧道等效为弹性地基梁，基于Winkler模型，计算隧道的纵向变形。但Winkler模型过于简化没有考虑地基的剪切刚度。黄栩等[11]采用更精确的Kerr模型研究开挖卸载引起的下卧隧道纵向变形。但目前的研究中将下卧隧道等效为弹性地基梁的假设过于简化，没有考虑盾构隧道的管片结构。魏新江等[15]在研究地面堆载对临近地铁隧道的影响时，采用了一种可综合考虑刚体转动效应和剪切错台效应的盾构隧道变形模型，研究发现该模型的计算值要比弹性地基梁模型更接近实测值，也更能反映隧道实际变形模式。但目前在基坑开挖引起下卧隧道变形的研究过程中能同时考虑剪切错台和刚体转动协同变形的研究较少，因此，本文作者引入可综合考虑盾构隧道管片环转动和错台2种变形效应的协同变形模型，采用Mindlin解计算基坑开挖对下卧盾构隧道的附加荷载，结合最小势能原理建立隧道变形的变分控制方程。推导出隧道的纵向变形量、环间剪切力、错台量和环间转角的计算公式。利用复合辛普森求积公式编写相应的Matlab数值计算程序进行求解。选取3组典型案例进行计算分析，将计算值与实测值进行对比，验证该方法的可靠性。

1 基坑开挖引起的盾构隧道附加荷载

基坑开挖对下卧盾构隧道影响的示意图如图1所示。在盾构隧道上方开挖矩形基坑，在地面基坑中心O处建立坐标系，x和y轴分别垂直和平行于隧道轴线，z轴以竖直向下为正方向。沿y轴方向的基坑开挖长度为L，沿x轴方向的基坑开挖长度为B，基坑开挖深度为d。基坑与盾构隧道位置关系图如图2所示。基坑底部以下围护结构插入深度为d0，基坑围护结构总高度为H(H=d+d0)，开挖面与隧道的最小净距为s，盾构隧道外径为D，隧道轴线埋深为h(h=s+D/2)。隧道轴线与基坑中心的水平距离为a，由此可得隧道轴线上任意一点的位置为(a，l，h)，l为该点在此坐标中对应的y轴坐标值。

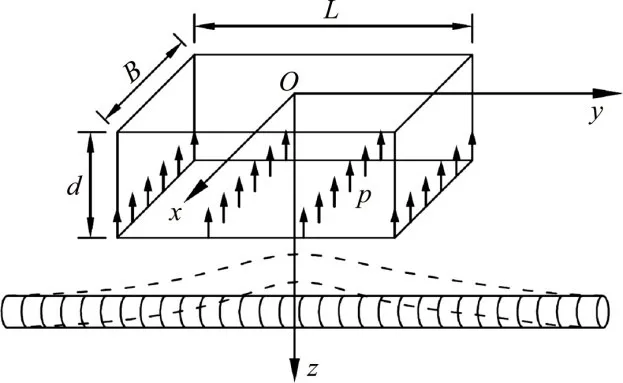
图1 基坑开挖对下卧盾构隧道影响的示意图Fig.1 Schematic diagram for influence of foundation pit excavation on underlying shield tunnel

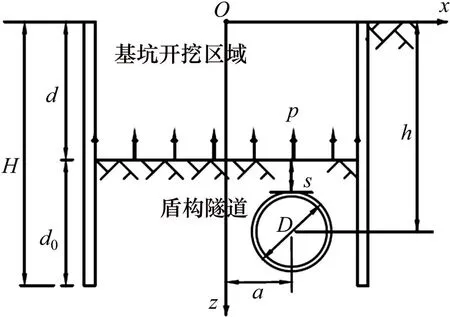
图2 基坑与盾构隧道位置关系图Fig.2 Position relationship between pit and tunnel

假设：

1)地基土为均匀连续、各向同性的半无限弹性体；

2)在计算基坑开挖对土体产生的附加应力时，不考虑隧道存在的影响。

考虑到实际工程中隧道上方基坑支护体系刚度较大以及底部围护结构和隔离墙的遮拦效应，根据计算，基坑侧壁卸载对基坑下卧隧道的竖向变形影响很小，可以忽略不计，故将基坑开挖的卸载效应简化为基坑底部施加竖直向上的均布荷载，均布荷载可根据下式进行计算：

式中：p为基坑底部卸载(kN/m2)；γ为土的重度(kN/m2)，可取开挖土体的加权平均值；α0为残余应力系数[16]，该系数可以用来考虑基坑底部应力不完全释放的情况，其取值方法可参考文献[16]。

根据Mindlin应力解[17]，在半无限弹性体中(x1,y1,z1)处作用一单位力，计算点(x,y,z)处产生的竖向附加应力为

根据式(1)和式(2)可得：在基坑底部某点(ξ，η，d)处，卸载p作用下，隧道处(a，l，h)的竖向附加应力P(l)为

2 下卧盾构隧道纵向变形计算

2.1 考虑转动和错台的管片环协同变形模型

将盾构隧道每一节管片环简化为弹性地基短梁，管片环间由法向弹簧和剪切弹簧连接[15]。盾构隧道协同变形示意图如图3所示。相邻管片之间既会产生相对转角，也会发生相对错台，而隧道纵向变形由相邻管片环之间剪切错台和刚体转动组合形成。当相邻管片环之间总的相对竖向位移为δ，由管片环刚体转动产生的相对竖向位移为δ1，由管片环错台产生的相对竖向位移为δ2，则满足δ=δ1+δ2。令δ1=jδ，j为管片环刚体转动效应比例系数，表示相邻管片环之间刚体转动产生的相对竖向位移与总的相对竖向位移之比。当j=0时，相邻管片环之间没有相对转动，为完全剪切错台的变形模式，与周顺华等[18]提出的隧道错台变形模型一致；当j=1时，位移完全由相邻管片转动产生，为完全的管片转动变形模式，与王如路[19]计算环缝张开量时假定的隧道变形模式相同。

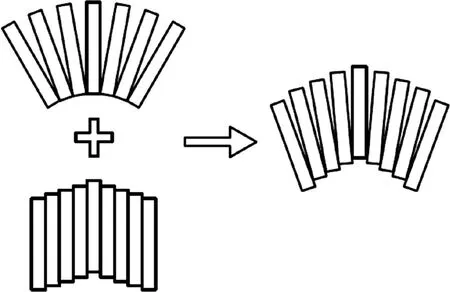
图3 盾构隧道协同变形示意图Fig.3 Shield tunnel cooperative deformation diagram

盾构隧道剪切错台和刚体转动协同变形计算模型如图4所示。编号为m和m+1的相邻衬砌环相对竖向位移为δm，这组相邻管片环之间的相对竖向位移可视为由刚体转动引起的竖向位移δm1和剪切错台引起的竖向位移δm2组成，即δm=δm1+δm2。

假设土体与隧道满足变形协调条件，隧道位移wt(l)与对应位置的土体位移w(l)相等：

式中：l为隧道纵向的计算位置，以基坑开挖中心为零点沿y轴方向为正。

图4 盾构隧道剪切错台和刚体转动协同变形计算模型Fig.4 Cooperative deformation calculation model for shield tunneling shearing dislocation and rigid body rotation

相邻管片处的隧道竖向位移差即为相邻管片环的相对竖向位移，由此环间相对竖向位移δm可表示为

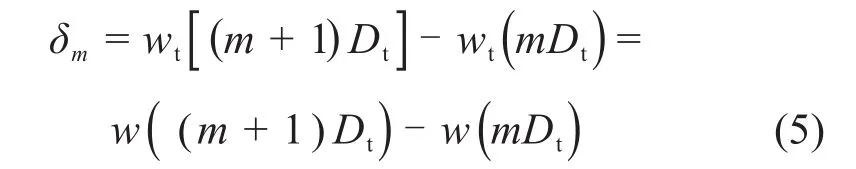
式中：Dt为管片环的环宽。

当衬砌环间转动角度θm较小时，假设sinθ=θ，cosθ=1。因此，衬砌环间刚体转动引起的竖向位移量计算公式为

将δm1=jδm代入式(6)得：

根据隧道变形和环间剪切刚度、环间抗拉刚度及基床系数，可以得到环间剪切力为

环间最大拉力为

地层抗力为

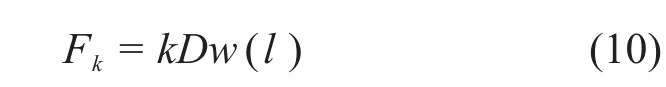
式中：ks和kt分别为隧道的环间剪切刚度和环间抗拉刚度，取值方法可参考文献[20]；k为土的基床系数，采用 Vesic公式[21]计算，k=E0为地基土的变形模量，E0=Es为土的压缩模量；EtIt为隧道的等效抗弯刚度，根据叶飞等[22]的研究盾构隧道等效刚度可以根据以下公式计算得到：

式中：Ec为管片弹性模量；nb为纵向螺栓数；Kb为接头螺栓的平均线刚度；As为隧道横截面面积；不考虑隧道水平直径和竖直直径发生变化时，λ1=tD(A1+A2-A3-A4-A5)，λ2=tD(A1+A2+A3+A4+A5)，A1= πD2/16，A2= πD2sin2ψ/8，A3=D2ψ/8，A4=D2ψsin2ψ/4，A5=3D2sinψcosψ/8，其中ψ为管片环中心轴位置参数，取值方法可参考文献[22]；t为管片厚度。

2.2 盾构隧道变形总势能

根据盾构隧道纵向变形的过程分析，盾构隧道变形的总势能具体可以由以下4部分组成。

1)基坑开挖引起的附加荷载的功为

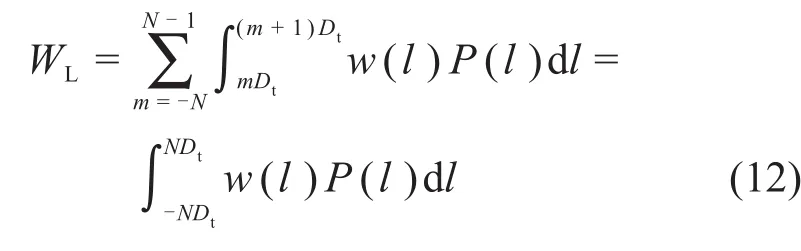
式中：N为基坑开挖中心单侧的隧道管片计算环数，与基坑开挖的影响范围有关，理论上N取值越大，计算精度越高，但是相应计算量也会增大，计算效率降低。

2)克服地层抗力的功为

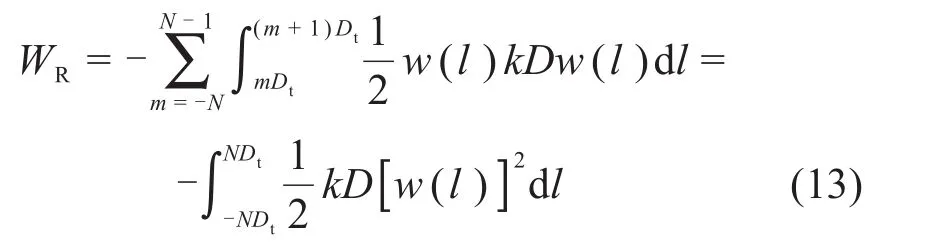
3)克服环间剪切力的功为

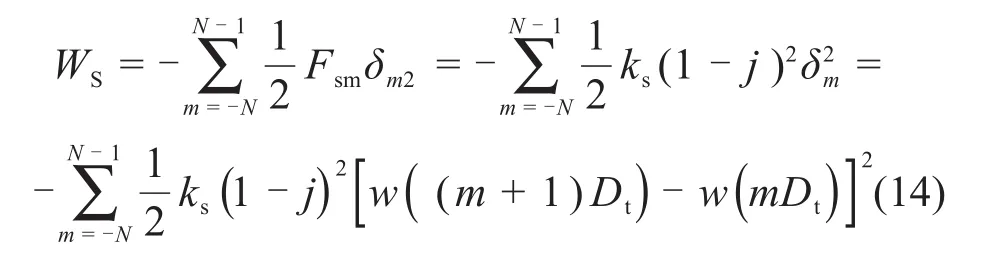
4)克服环间拉力的功为

因此，得到

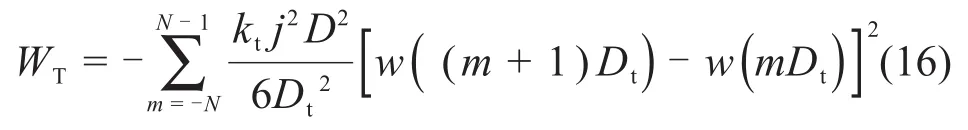
下卧盾构隧道变形的总势能为

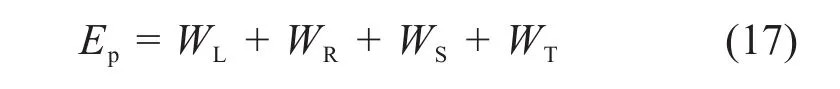
2.3 盾构隧道纵向位移函数傅里叶展开

假设盾构隧道纵向位移关于基坑开挖中点对称，并按傅里叶级数展开得到

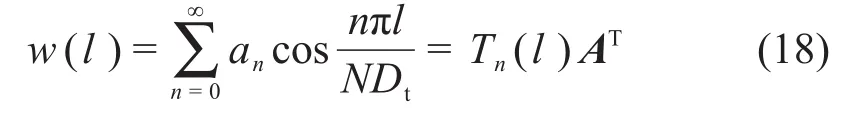
2.4 变分控制方程求解

基于最小势能原理将总势能Ep对各待定系数取极值：

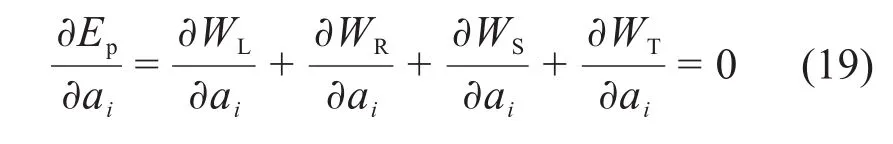
式中：i=1，2，3，…，n，ai为矩阵A中的第i个元素，即隧道纵向位移函数多项式的系数。

由式(19)求解可得控制方程：

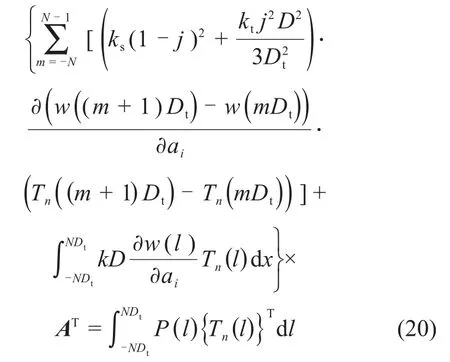
简写为矩阵形式为：

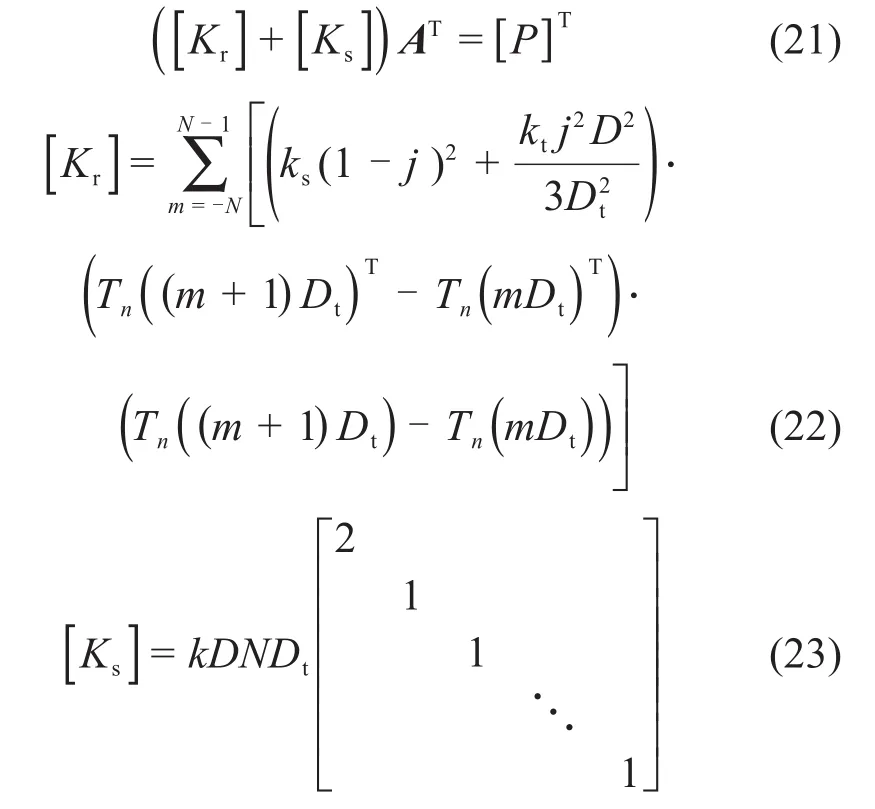
式中：[Kr]AT为隧道环间相互作用效应；[Ks]AT为土体抗力作用效应；[P]T为附加荷载对隧道衬砌作用效应，

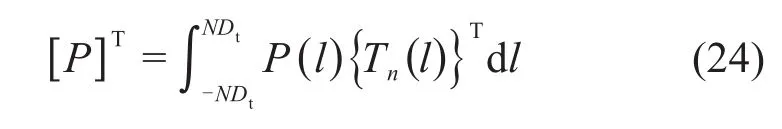
由式(21)计算可得到待定系数矩阵AT：

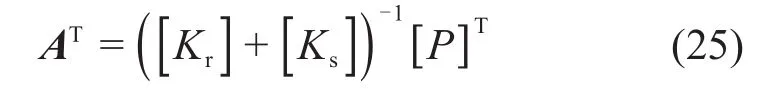
将待定系数矩阵AT代入式(18)即可得到隧道的纵向位移函数：

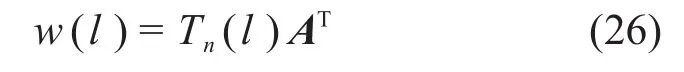
相邻盾构管片之间错台量为

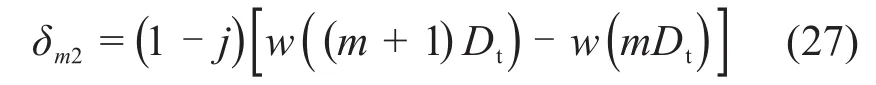
相邻盾构管片之间的剪切力Q为

上述计算方法可通过Matlab编程实现数值运算，其中积分运算步骤中利用复合辛普森求积公式，采用满足精度要求的积分步长进行数值积分。

3 实例验证及分析

由于基坑开挖对下卧既有隧道产生的纵向变形影响以竖向隆起为主，因此，选取3个基坑跨越盾构隧道的工程实例，采用本文方法计算基坑开挖引起的下卧盾构隧道竖向位移曲线，并与其实测曲线进行对比，以验证本文方法的正确性。同时与文献[18]方法的计算值及根据文献[19]刚体转动变形假定得到的计算值进行对比。

3.1 工程实例1

杭州市延安路某地下通道一期工程基坑L=11.4 m，B=14.83 m，d=8.2 m。地铁1号线左线隧道从基坑下方正交穿过，盾构隧道的10环管片位于开挖区间的正下方。隧道顶部与基坑底部开挖面最小净距离为3.9 m[6]。盾构隧道衬砌外径D=6.2 m，采用C50混凝土管片，厚度t=0.35 m，环宽Dt=1.2 m；管片环之间由16根M30纵向螺栓连接[23]。根据计算得到ks=7.45×105kN/m，kt=1.94×106kN/m，EtIt=1.1×108kN·m2。根据实际工程地质情况，土体重度取加权平均值γ=18.4 kN/m3，土的泊松比μ=0.35。水泥土搅拌桩对坑底土体、坑底上部土体以及围护结构外侧土体都进行了满堂水泥土加固，考虑部分水泥土加固作用土体压缩模量取Es=20 MPa[24]。卸载的残余应力系数取α0=0.3。

图5所示为实例1的隧道纵向隆起变形计算值与实测数据的对比。由图5可知，本文计算结果与实测结果吻合，此时，刚体转动效应比例系数j=0.2，即盾构隧道管片环刚体转动变形引起的纵向隆起变形占20%，管片环错台引起的隧道纵向隆起变形占80%。实测数据显示，基坑开挖引起的隧道最大隆起变形出现在开挖区间内，最大值为3.1 mm。基坑开挖中心附近的隧道隆起变形较大，向两侧递减，隧道隆起变形曲线大致呈正态分布。隧道隆起范围为基坑开挖中心向两侧各25～30 m。

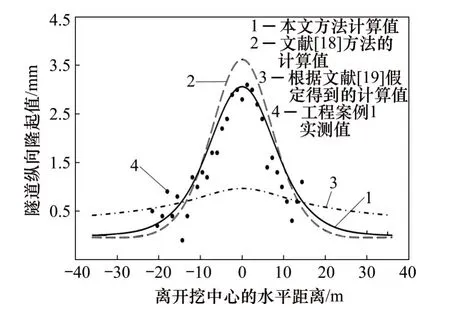
图5 实例1盾构隧道纵向隆起变形计算值对比Fig.5 Calculation and comparison of longitudinal heave deformation of shield tunnel in Case 1

当j=0时，本文计算模型退化成衬砌错台变形模型[18]；当j=1时，本文计算模型退化成管片环刚体转动模型[19]。故文献[18]的错台模型和根据文献[19]刚体转动变形假定得到的计算模型为本文计算模型的2个特解。分别利用错台模型[18]和根据刚体转动变形假定[19]得到的计算模型对实例1中的隧道隆起变形进行计算，衬砌错台计算模型得到的计算曲线最大值为3.62 mm，大于实测值和本文方法计算值。错台模型计算得到的隧道隆起范围比本文方法的小。根据管片环刚体转动变形假定得到的计算曲线明显与实测数据不符，最大计算值偏小，而影响范围偏大。

图6所示为实例1中不同N时本文方法计算得到的最大隆起变形变化曲线。由图6可知，当隧道计算环数较小时，本文方法计算得到的最大隆起变形较大，随着计算环数增加，最大隆起变形的计算值显著减小，当N增大至25环以上，最大隆起变形的计算值收敛于3.06 mm，并趋于稳定，收敛值接近于实测值。

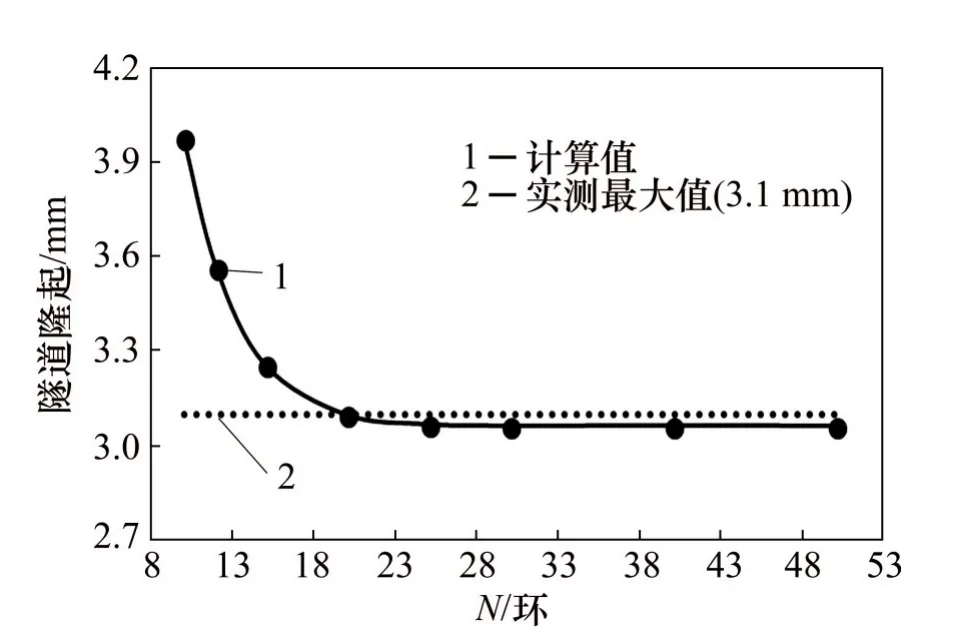
图6 实例1中不同N时最大隆起变形计算值的收敛情况Fig.6 Convergence of calculated maximum uplift with different N in Case 1

盾构隧道环间错台量和环间转角关系到隧道结构和防水体系的安全。环间错台量和转角越大，隧道发生渗漏水的概率越大，因此，对隧道错台量和转角的估算非常有必要。图7所示为本文方法计算得到盾构隧道管片错台量和环间转角。由图7可知，在隧道水平位移最大值处的管片错台量和环间转角均接近于0，即在开挖中心处的管片环之间几乎没有相对错台和相对转动。但是，开挖中心附近的错台量和转角增加较为急剧；管片最大错台量为0.21 mm，最大环间转角为0.045°，均出现在隧道隆起位移曲线的2个反弯点附近，位于基坑开挖区域边缘外侧，距离开挖中心约7 m。

图7 实例1中盾构隧道管片环间错台量和转角Fig.7 Dislocation and rotation angle among shield tunnel segment rings in Case 1

图8所示为本文方法计算得到的盾构隧道环间剪切力。由图8可以看出：盾构隧道环间剪切力的变化规律和隧道错台量的变化规律一致；隧道管片环错台量最大处的剪切力最大，最大值为159.53 kN。

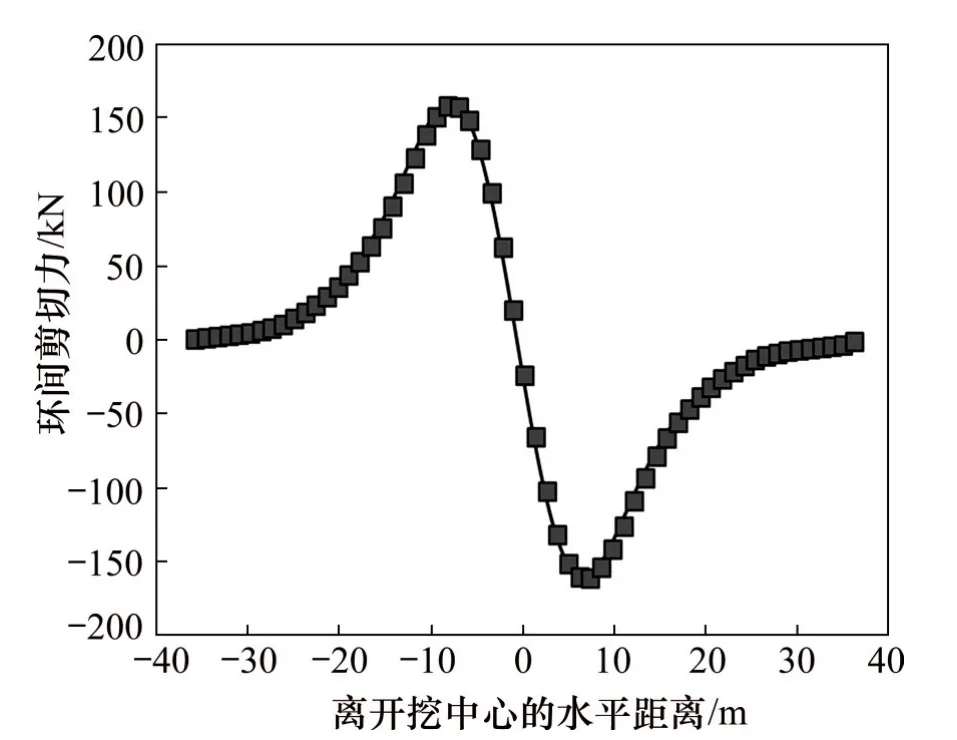
图8 实例1中盾构隧道环间剪切力Fig.8 Shearing force among shield tunnel segment rings in Case 1

3.2 工程实例2

上海市外滩通道南段采用明挖法施工，跨越既有的延安东路隧道。基坑采用隔离墙分割为数块分区开挖，跨越北线的开挖区域在分析时可简化为：隧道与基坑开挖区域垂直交叉，开挖区域L=10 m，B=50 m，d=11 m[6]。隧道顶部与基坑底部开挖面最小净距离为5.5 m。延安东路盾构隧道衬砌外径D=11 m，衬砌厚度t=0.55 m，属于大直径盾构隧道。环宽Dt=1 m；管片环与环之间由32根M36纵向螺栓相接[25]。根据计算得到ks=2.14×106kN/m，kt=5.59×106kN/m，EtIt=9.52×108kN·m2。根据实际工程地质情况，土体重度γ=17.87 kN/m3，土的泊松比μ=0.4，土的压缩模量Es=6.04 MPa。卸载的残余应力系数α0=0.1。

延安东路隧道北线约有10环管片位于开挖区间的正下方。图9所示为实例2中不同N时本文方法计算得到的最大隆起变形变化曲线。由图9可知，当N增大至50环以上，最大隆起变形计算值收敛并趋于稳定，收敛值为6.20 mm。综合考虑计算精度和计算速度，在与实测数据比较计算中取N=70环。实例2中盾构隧道纵向隆起变形计算值对比如图10所示。可见：计算值与实测值较吻合，此时，刚体转动效应比例系数j=0.1，即隧道管片环刚体转动变形引起的纵向隆起变形占10%，管片环错台引起的隧道纵向隆起变形占90%。实测数据显示，隧道纵向隆起最大值6.42 mm，出现在距开挖中心4 m左右处。虽然开挖中心处隧道隆起反而有所减小，但在开挖范围内依然是隧道隆起变形最大的位置。基坑开挖引起隧道隆起变形的影响范围约为基坑开挖中心两侧各50 m内。

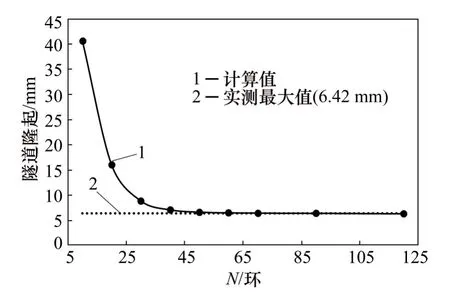
图9 实例2中不同N下最大隆起计算值的收敛情况Fig.9 Convergence of calculated maximum uplift with different N in Case 2

图10 实例2中盾构隧道纵向隆起变形计算值对比Fig.10 Calculation and comparison of longitudinal heave deformation of shield tunnel in Case 2

由图10可知，文献[18]的管片错台模型计算得到的隧道纵向隆起变化较大，最大隆起变形也较大，隆起范围比较集中。根据文献[19]管片环刚体转动变形假设计算得到的隧道隆起变形曲线变化比较缓和，隆起范围偏大。总体上看，本文方法的预测曲线更接近实测值。

图11所示为本文方法计算得到的延安东路北线隧道盾构管片错台量和环间转角。由图11可知：距开挖中心的水平距离约11 m处，环间错台量和转角最大，最大值分别为0.220 mm和0.024 5°。图12所示为本文方法计算得到的环间剪切力。由图2可知：环间剪切力最大值为472.73 kN。管片环间转角、错台量和环间剪切力的变化规律同工程实例1基本相同。

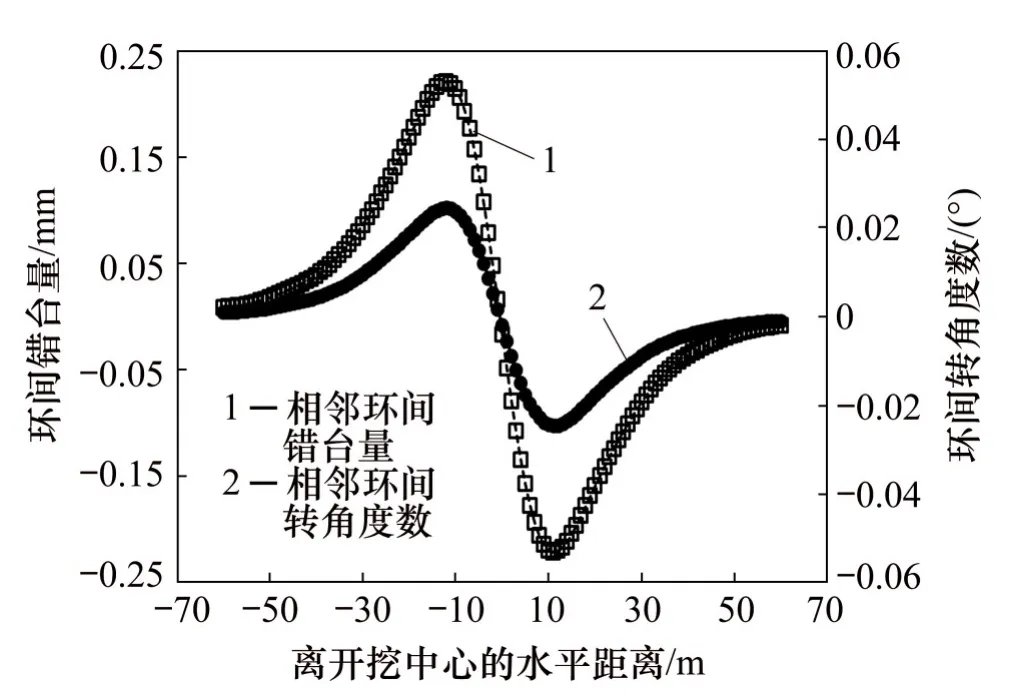
图11 实例2中盾构隧道管片环间错台量和转角Fig.11 Dislocation and rotation angle among shield tunnel segment rings in Case 2

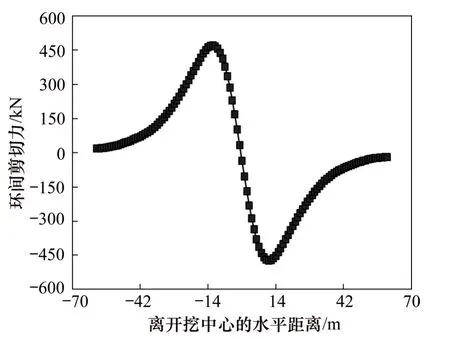
图12 实例2中盾构隧道环间剪切力Fig.12 Shearing force among shield tunnel segment rings in Case 2

3.3 工程实例3

杭州金沙湖绿轴下沉广场基坑工程位于已建杭州地铁1号线上方，本案例所研究的基坑开挖核心区B=30 m，开挖深度5.3 m。有50环隧道管片位于开挖区域下方[26]，即开挖区域长度L=60 m。核心区基坑位于盾构隧道正上方，关于上下行中线对称。上下行隧道轴线间距为15 m，即左右线隧道轴线与基坑开挖中心水平距离都为7.5 m。基坑底距隧道顶部与基坑底部开挖面最小净距离分别为3.3 m和4.3 m[26]。杭州地铁1号线盾构隧道衬砌外径D=6.2 m，采用C50混凝土管片，厚度t=0.35 m，环宽Dt=1.2 m；管片环之间由16根M30纵向螺栓连接[23]。根据计算得到ks=7.45×105kN/m，kt=1.94×106kN/m，EtIt=1.1×108kN·m2。根据实际工程地质情况取加权平均值，土体重度γ=18.4 kN/m3，土的泊松比μ=0.35，土的压缩模量取Es=7 MPa。基坑开挖面积较大，卸载的残余应力系数取α0=0。基坑紧邻杭州地铁1号线下沙西站，左线隧道位于开挖区域下方的部分连接车站主体结构，车站对隧道变形产生了较明显的限制作用[26]，而右线隧道上方基坑边缘距车站较远，最短距离约为50环(60 m)，车站对基坑下方隧道的约束作用较小，故本文选取右线监测数据与本文方法进行对比。

图13所示为实例3中不同N时本文方法计算得到的最大隆起变形变化曲线。由图13可知，当N增大至60环以上，最大隆起变形的计算值收敛并趋于稳定，收敛值为5.80 mm。综合考虑计算精度和计算速度，在与实测数据比较计算中取N=85环。实例3中盾构隧道纵向隆起变形计算对比如图14所示。由图14可知，本文方法计算值与实测值较吻合，此时，刚体转动效应比例系数j=0.3，即盾构隧道管片环刚体转动变形引起的纵向隆起变形占30%，管片环错台引起的隧道纵向隆起变形占70%。实测数据显示，隧道纵向隆起最大值6.3 mm，出现在距开挖中心附近。基坑开挖引起隧道隆起变形的影响范围为距开挖中心两侧各70～75 m。

图13 实例3中不同N时本文方法计算得到的最大隆起变形的收敛情况Fig.13 Convergence of calculated maximum uplift with different N in Case 3

由图14还可知，文献[18]方法计算得到的开挖范围内的隧道隆起变形偏大，整条隧道的隆起范围偏小。根据文献[19]假定得到的计算曲线与实测数据差距较大。

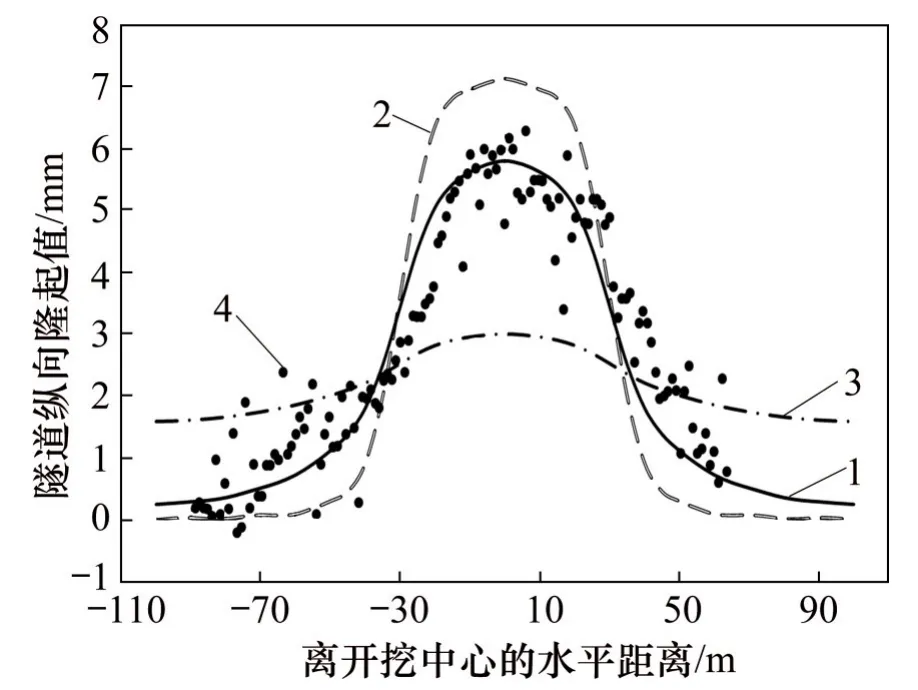
图14 实例3中盾构隧道纵向隆起变形计算对比Fig.14 Calculation and comparison of longitudinal heave deformation of shield tunnel in Case 3

图15 工程案例3中盾构隧道管片环间错台量和转角Fig.15 Dislocation and rotation angle among shield tunnel segment rings in Case 3

图15所示为本文方法计算得到的案例3中地铁1号线盾构管片错台量和环间转角。由图15可知：最大管片错台量和环间转角发生在距基坑开挖中心约30 m处，最大值分别为0.656 mm和0.234 2°。

图16所示为本文方法计算的环间剪切力。由图16可知：环间剪切力最大值为488.33 kN。与前2个工程案例规律有所不同的是，开挖中心附近的管片错台量、环间转角和环间剪切力变化趋势稍有缓和，这与该案例基坑沿隧道轴线方向长度较长，开挖中心附近有多环管片整体发生隆起，而环间的相对位移较小有关。

图16 工程案例3中盾构隧道环间剪切力Fig.16 Shearing force among shield tunnel segment rings in Case 3

3.4 参数N与隧道影响范围的关系及其物理意义

本文方法中，受基坑开挖影响的隧道管片计算环数为2N，即N为基坑开挖中心一侧的隧道管片计算环数，也就是计算过程中假定隧道受影响范围的一半。理论上，N取值越大，计算过程中考虑的隧道范围越长，计算精度越高，更贴近实际情况。但是，相应计算量也会增大，计算效率受影响。由图6、图9和图13可知：随着N增大，隧道隆起变形计算值会收敛于最终值，收敛值与实测值非常接近。当计算值随着N增大收敛并趋于稳定时，可以认为基坑开挖引起隧道隆起的影响范围已被包括在计算范围之内，此时的N值即可认为是开挖中心一侧的隧道影响范围。

实例1的实测数据(图5)显示：开挖中心一侧隧道隆起影响范围为开挖宽度的2.2倍[6](26.4 m)，由图6可知：当计算值开始趋于稳定时，N=25环，因此，根据管片环宽1.2 m，可得隧道隆起影响范围为30 m。实例2的实测数据(图10)显示：开挖中心一侧隧道隆起影响范围约为50 m。由图9可知，当计算值开始趋于稳定时，N=50环，因此，根据管片环宽1 m，可得隧道隆起影响范围为50 m。实例3的实测数据(图14)显示：开挖中心一侧的隧道隆起影响范围为70～75 m。由图13可知，计算值开始趋于稳定时，N=60环，因此，根据管片环宽1.2 m，可得隧道隆起影响范围72 m。由此可见，根据计算值开始趋于稳定时的N值预测得到的影响范围与实测结果吻合。该方法既可以用于预测基坑开挖引起下卧盾构隧道隆起的影响范围，也可以用于确定本文方法计算参数N的取值。

3.5 管片环刚体转动效应比例j的影响因素分析

本文方法中，隧道的变形模型是管片环错台和刚体转动协同变形模型，计算参数j代表盾构隧道变形过程中管片环刚体转动产生的竖向位移占总的隧道竖向位移的比例。该参数在协同变形的模型中反映了错台效应和刚体转动效应的分配比例，是描述隧道纵向变形形式的重要参数。以实例3的工况为例，仅改变参数j，得到不同j时的隧道纵向变形曲线，如图17所示。

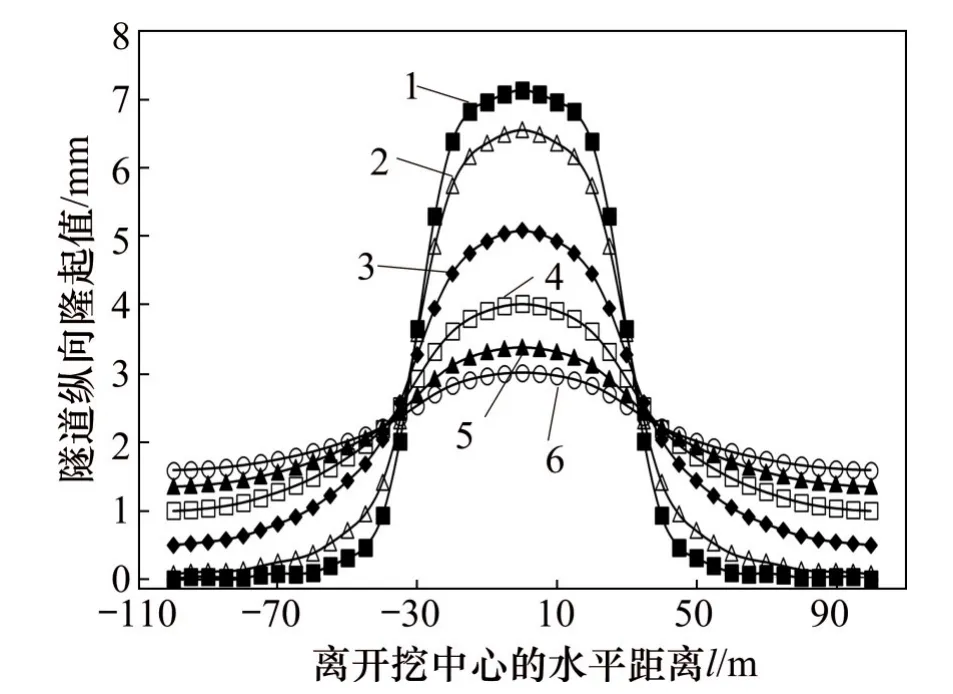
图17 不同j的盾构隧道纵向变形曲线Fig.17 Longitudinal deformation curve of shield tunnel with different j

由图17可知：当j较小时，隧道隆起范围主要集中在基坑开挖范围附近。当j较大时，隧道隆起影响范围更广。随着j增大，隧道最大隆起变形逐渐减小，在此案例中，剪切错台模型(j=0)与刚体转动模型(j=1)计算得到的隧道最大隆起变形相差4.12 mm。

从3个工程实例可以发现：此类实际工程中，盾构隧道纵向变形主要还是以错台变形为主，以刚体转动变形为辅。这与王如路[19]根据上海地铁隧道变形长期监测得到的结论一致。管片环刚体转动效应产生的竖向位移占总位移的10%～30%，而管片环间错台效应产生的竖向位移占70%～90%。

理论上，本文盾构隧道纵向位移函数傅里叶级数展开式(式(18))有无穷项，实际计算中应取其前若干项进行计算，所代入的项数越多，计算精度越高。为了兼顾了精度和运算效率，本文算例分析中取式(18)前10项代入进行计算，即式(21)～(25)中矩阵[Kr]和[Ks]为10阶方阵，与更高一阶矩阵的计算结果相比，相对误差在1%以内，满足工程计算的精度要求。