基于观察物体视角培养学生的空间观念
2019-10-15陈美彩
陈美彩


摘要: 源于一道求表面积的错题,分析错因发现学生在学习表面积计算过程中存在:生活经验缺乏,空间思维模糊;表面积概念浅薄,空间想象浅表;动手能力薄弱,空间模型崩塌;应用能力死板,空间观念缺失等主要问题。教师利用观察物体的视角培养学生的空间观念,提出以下教学建议:原型提取,丰富感知;维度转换,建构模型;操作实践,发展空間观念;在应用中形成空间观念;渗透数学思想:转化思想,同表面异立体,灵活适应变化。等几个方面来促进三维立体与二维平面之间的转化。
关键词: 表面积;变化;观察物体
一、源于一道错题
观察物体和表面积在教学课本里是分成两个不同的单元。但在教学时其本质有许多联系。在教学中,教师如果能经常鼓励学生学会用观察物体的视角去解决表面积的问题,那么表面积的学习便会轻松许多。
在人教版五年级下册第26页12题求颁奖台的面积这题。学生在尝试解决过程过出现了许多错误,例题如下:
【案例叙述】
要求:
1.选择你最喜欢的方法,计算面积。
2.完成后说一说你是怎么想的。
3.和同桌交流、比较方法的差异。
方法1:【观察法】(六个方向观察计算总面积)
上:40×40×3=4800平方米
下:不涂
左:40×65=2600平方米
右:40×65=2600平方米
前:40×40×2+40×65=5800平方米
后:40×40×2+40×65=5800平方米
方法2:【找到共同面】
正方形有四个面相同:(红油漆计算方法不同,黄油漆计算方法同上)
40×40×4=6400平方米
25×40+10×40+55×40=3600平方米
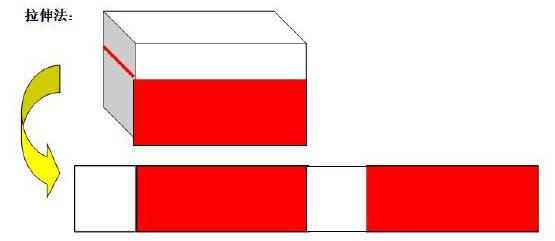
方法3:【拉伸法】
红油漆=长×宽
长=40+40+25+40+10+40+55=250米
250×40=10000平方米
(表1:立体图形求表面积正确率统计)
人数统计 方法1 方法2 方法3 错误方法
占全体被测百分率统计 43.9% 10.5% 6.4% 39.2%
如上三种正确的方法主要出现在学生的作业本上,选择方法1的占多数。仔细思考发现如上三种方法都有其类同之处。观察法和找相同面都需要学生利用空间观念。仔细分析每个面所对应的长和宽,拉伸法则是利用对三维立体转化为二维平面的一种思考方法,即观察法的后延伸。
二、基于观察物体的视角培养空间观念的策略
观察图形是获取图形各方面信息的基础。在观察中能直观感知图形的形状、特征、位置关系等,从而建立起立体图形的表象。长、正方形均由六个面组成,在观察中找到相对应的量,在想象中丰富对立体图形的感知,便于理解。通过实践,试想通过以下几种策略突破表面积的难点。
(一)借助观察物体视角:原型提取,丰富感知
由于包装时纸板有部分折叠,若裁剪出来,会多出一些面,影响学生对表面积的认知。因此在教学时,我尝试着让学生描出英语磁带盒的表面,在描一描的过程中观察、感知、思考,自主构建表面积的概念。
【英语磁带盒】操作要求:从上下左右前后六个面观察英语磁带盒,再把它压在白纸上,用笔描出每个面,并填写表格。
【研究学案1】 根据你所描的,把下列表格填写完整。
展示讨论:为什么有些同学的作品既清楚,又不重不漏?
由于学生认知水平的多元性和差异性,学生描出长方体的表面也各不相同。此时,需要教师及时引导,在反馈中问:“你更喜欢哪种描法,为什么?”在对比中感知长方体各面的特点,明确翻转描法的优越性,从而清楚表面积的含义。在优化中,鼓励学生重新尝试以翻转法描表面,丰富感知。
(二)基于观察物体视角:维度转换,建构模型
我们需要有意地培养学生学会从实物中抽象出图形,在图形中想象出实物,发展跨越维度的空间观念。因此笔者在教学表面积时,做过一些尝试,希望打通二维平面和三维空间之间的关系。
(三)运用观察物体视角:操作实践,发展空间观念
1. 三维立体图形之间的转化
【研究学案4】 要求:用12个棱长为1cm的小正方体摆出不同的长方体,并求出表面积。(每个小正方体1个面的面积是1平方米)
【研究学案5】 要求:由12个小正方体摆出一个长方体,然后从六个方向观察物体,求出每个方向观察到的面积,最后求出表面积。并找一找这些图形的表面积计算方法有没有异同之处。(每个小正方体1个面的面积是1平方米)
对比研学方案4和5,得出统一结论:长方体的表面积=(长×宽+长×高+宽×高)×2。同样个数的小正方体,摆成不同的长方体,通过不同的角度观察,得出不同的表面积。学生通过合作观察、记录分析,对长方体表面积的计算也有了更深入的认知。
2. 三维立体转化为二维平面
观察组合图形面积的计算,同样可以使用观察法。若能在观察法的基础上促进三维立体转化为二维平面的计算,那么对于学生的空间观念的提升又是一个质的飞跃。
[案例2] 把一个长30米,宽20米,高3米的游泳池,延深2米处在墙壁的四周涂油漆,需要涂多少平方米的油漆?
拉伸法:
【研究学案6】 要求:把这个长方体游泳池的侧面拉伸,变成一个长方形。利用六个方向看到的面积推导,侧面积的计算简便方法。
把游泳池的四周转化为长方形,求长方形的面积即是长方体的表面积。把三维的立体视图转化为二维的平面视图,组合成为一个整体。再利用长×宽就可以计算出表面积的大小。若学生学会利用转化思想,就能把复杂的问题简单化,那么学生空间观念的培养就会水到渠成。
(四)利用观察物体视角:在应用中形成空间观念
现实中有许多利用长、正方形表面积的知识解决的实际问题,有些实际物体需要涂色6个面,有些5个面或更少。这就需要学生先思考,確定哪几个面的面积需要计算,再运用数学知识解决问题,在应用中感受数学的生活化,强化方法。
[案例4] 设计衣柜
要求:根据你家里的住房条件,设计一款实用的衣柜,和同桌说一说,你家的衣柜表面积至少需要哪几个面。为什么?
生1:六个面,上下、前后、左右。
生2:五个面,上下,前、左右,因为,后面靠着墙可以省材料。
生3:四个面,上下,前、左。因为我家的衣柜后面和右面都靠着墙。
生4:三个面,上,前、左。因为我家的衣柜后面和右面都靠着墙,下面靠着地板。
生5:二个面,上+前。因为我家的衣柜因为我家的衣柜后面、左、右面都靠着墙,下面靠着地板。
师:你们的设计各有千秋,我们可以根据个人爱好选择不同的衣柜。
教师通过设计衣柜这样一个具体的实物,帮助学生在应用中学会分析具体问题,运用已有的知识,进行讨论思考。不仅丰富了生活经验,激发了学习的兴趣,也培养了空间观念。
(五)渗透数学思想
数学思想的渗透能帮助学生加深对概念的理解,立体图形表面积的计算出现比较多的思想方法就是转化。在变化中找到解决问题的途径就是转化思想的精髓。
【转化思想】 同表面异立体,灵活适应变化
观察往往比记忆公式有效得多。题型千变万化,有些并不是通过代入公式就可以解决的。面对这类题目,学生往往会出现很多问题。因此要教会学生以不变应万变,抓住观察物体之间的联系。
[案例5] 比较下面两个图形的表面积大小。
小结 凡是在正方体顶点处去掉小正方体,它的表面积都没有变化。
其实,无需计算,只要从六个方向进行观察,利用转化思想,就会发现上下两个图形的表面积相等。
举一反三,凡是在长方体顶点处挖去一个正方体,表面积的大小是不变的,但是体积大小是变化的。变化的题目也可以利用观察法,利用上下、前后、左右表格法计算他们的表面积是否发生变化。因此,以观察物体的视角来计算表面积,能更好的整合空间与图形这一块的学习内容,更有效地培养学生的空间观念,突破表面积计算的学习困境。
参考文献:
[1]高远望.变“剪”为“描”,探究长方体表面积[J].湖南教育(下旬刊),2012,(1):31-32.
[2]吕霞.冲破“表面积计算”的困扰——以“长方体和正方体的表面积”为例谈立体图形的表面积计算[J].中小学数学(小学版),2011,(9):47-49.
[3]江世春.让学生在自主学习中享受数学--"长方体表面积的计算"教学片断与评析[J].小学青年教师,2005,(6):35.DOI:10.3969/j.issn.1003-2193.2005.06.028.
[4]田建设.重视多种活动的安排 培养学生的空间观念——“长方体的表面积”一课教学有感[J].新课程·上旬,2015,(7):248.
[5]丘丽娟.如何发展学生的空间观念——以“长方体的表面积”教学为例[J].中小学数学,2013,(5):21-22.
